I. 1351. Negative Numbers in Statistically Ordered Matrix
1. Title
1351. Negative numbers in statistical ordered matrices
Give you a matrix grid of m * n whose elements are arranged in a non-increasing order, either by row or by column.
Please count and return the number of negative numbers in the grid.
2. Analysis
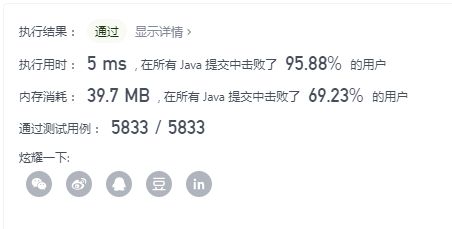
- The title has an important message: non-increasing order, I do not understand what to say at first, but after looking at the drawing, I found that it meant: non-strict monotonic decline.
- We can start from the upper right corner of the matrix, column by column. If a negative number is found, then all the numbers of the current column below this number are negative.
- The loop terminates if:
i
i
i and
j
j
JOne of them goes beyond the boundary, that is, when
i
>
=
m
or
person
j
<
0
I >= m or j < 0
When i>=m or j<0, the loop terminates.
3. Code
class Solution {
public int countNegatives(int[][] grid) {
int m = grid.length,n = grid[0].length;
int i = 0,j = n,count = 0;
while (i < m && j >= 0){
j--;
if (i >= m || j < 0){
break;
}
//Until the first negative number of the current column is found
while (i < m && grid[i][j] >= 0){
i++;
}
//When the first negative number is found, the number below this column is also negative.
count += m - i;
}
return count;
}
}
2. 1572. Sum of Matrix Diagonal Elements
1. Title
1572. Sum of matrix diagonal elements
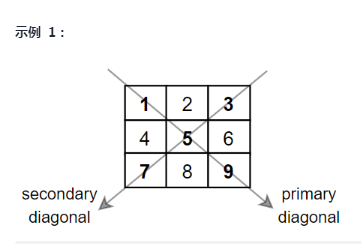
Give you a square matrix mat, and return the sum of the diagonal elements of the matrix.
Please return the sum of the elements on the principal and secondary diagonals of the matrix that are not on the principal diagonal.
2. Analysis
- Traversal starts at the upper left corner and the upper right corner, respectively: i = 0 , l = 0 , r = l e n g t h − 1 i = 0,l = 0,r = length - 1 i=0,l=0,r=length−1.
- Each time, add 1 line, left subscript l l l Move right, subscript to right r r r Move to the left, repeating the elements that are accumulated in the middle before processing.
- After all the rows have been accumulated, then according to the number of rows (the same as the number of columns) of the square matrix, we can determine if there are any elements that are duplicated in the middle. If the number of rows is odd, we can subtract the elements that are duplicated in the middle.
r
e
s
−
m
a
t
[
l
e
n
g
t
h
>
>
1
]
[
l
e
n
g
t
h
>
>
1
]
res - mat[length >> 1][length >> 1]
res−mat[length>>1][length>>1]
3. Code
class Solution {
public int diagonalSum(int[][] mat) {
int length = mat.length,res = 0;
int i = 0,l = 0,r = length - 1;
while (i < length){
res += mat[i][l] + mat[i][r];
i++;
l++;
r--;
}
//If the number of rows is odd, subtract the elements that repeat in the middle once
return (length & 1) == 0 ? res : res - mat[length >> 1][length >> 1];
}
}
3. 1672. Total assets of richest customers
1. Title
1672. Total assets of the richest clients
Give you an integer grid account of m x n, where accounts[i][j] is the number of assets that a customer has hosted at the jth bank. Return the total amount of assets owned by the richest customer.
The total amount of a customer's assets is the sum of the amount of assets they hold in each bank. The richest customers are those with the largest total assets.
2. Analysis
In other words, it calculates the sum of each one-dimensional array element in a two-dimensional array and returns the maximum value.
3. Code
class Solution {
public int maximumWealth(int[][] accounts) {
int max = 0;
for (int i = 0;i < accounts.length;i++){
int sum = 0;
for (int j = 0;j < accounts[i].length;j++){
sum += accounts[i][j];
}
max = max > sum ? max : sum;
}
return max;
}
}
IV. 766. toeplitz
1. Title
You are given a matrix of m x n matrices. Returns true if the matrix is a Toplitz matrix; Otherwise, return false.
If every element on the diagonal from the top left to the bottom right of a matrix is the same, then this matrix is a Toplitz matrix.
2. Analysis
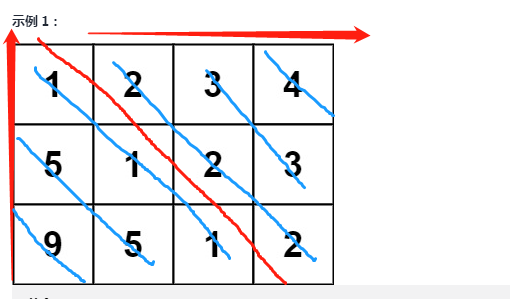
- You can think of a matrix as two parts (two parts separated by a red line), then traverse from the lower left corner to the upper right corner.
- Every Judgment
m
a
t
r
i
x
[
i
]
[
j
]
matrix[i][j]
matrix[i][j] and
m
a
t
r
i
x
[
i
−
1
]
[
j
−
1
]
matrix[i - 1][j - 1]
matrix[i_1][j_1], if equal, the row and column subscripts are added 1 until one of them is outside the bounds (beyond the length of the array).
3. Code
class Solution {
public boolean isToeplitzMatrix(int[][] matrix) {
int m = matrix.length,n = matrix[0].length;
int i,j,t;
for (i = m - 1;i >= 0;i--){
t = i;
j = 0;
t++;
j++;
while (t < m && j < n){
if (matrix[t][j] != matrix[t - 1][j - 1]){
return false;
}
t++;
j++;
}
}
for (j = 1;j < n;j++){
t = j;
i = 0;
i++;
t++;
while (i < m && t < n){
if (matrix[i][t] != matrix[i - 1][t - 1]){
return false;
}
i++;
t++;
}
}
return true;
}
}
5. 1380. Lucky numbers in matrices
1. Title
Give you a matrix of m * n with different numbers. Please return all the lucky numbers in the matrix in any order.
The lucky number is an element of a matrix that satisfies both of the following conditions:
Minimum of all elements in the same row
Largest of all elements in the same column
2. Analysis
- Find the minimum value for each row and record the minimum value and the corresponding column subscript.
- Then find the maximum value from the column of the record and save it in the List collection if the minimum value of the row is the same.
3. Code
class Solution {
public List<Integer> luckyNumbers (int[][] matrix) {
List<Integer> list = new ArrayList<>();
int i,j,rowMin,colMax = 0,colIndex = 0;
for (i = 0;i < matrix.length;i++){
rowMin = matrix[i][0];
for (j = 1;j < matrix[i].length;j++){
if (rowMin > matrix[i][j]){
rowMin = matrix[i][j];
colIndex = j;
}
}
colMax = matrix[0][colIndex];
for (j = 1;j < matrix.length;j++){
if (colMax < matrix[j][colIndex]){
colMax = matrix[j][colIndex];
}
}
if (rowMin == colMax){
list.add(colMax);
}
}
return list;
}
}
6. 1582. Special Positions in Binary Matrix
1. Title
1582.Special position in binary matrix
Give you a matrix mat of size rows x cols, where mat[i][j] is 0 or 1. Return the number of special positions in the matrix mat.
Special location definition: If mat[i][j] == 1 and all other elements in row I and column J are 0 (subscripts for rows and columns start at 0), location (i, j) is called a special location.
2. Analysis
- Traverses a two-dimensional array.
- When the current element traversed is 1, the current row and column are traversed internally to find out if there is one element in addition to this element, and if there is none, the count is added to 1.
3. Code
class Solution {
public int numSpecial(int[][] mat) {
//Define traversal Subscripts
int j,i = 0;
//Number of Matrix Rows
int rows = mat.length;
//Number of Matrix Columns
int cols = mat[i].length;
//Number of Special Locations
int count = 0;
for (i = 0;i < rows;i++){
inner:
for (j = 0;j < cols;j++){
if (mat[i][j] == 1){
//Traversing through all columns of row i, with a position of 1 in addition to the special position, directly jumps out of the current row cycle
for (int col = 0;col < cols;col++){
if (col == j){
continue;
} else if (mat[i][col] == 1){
break inner;
}
}
//Traversing through all rows of column j, with a position of 1 in addition to the special position, directly jumps out of the current row cycle
for (int row = 0;row < rows;row++){
if (row == i){
continue;
} else if (mat[row][j] == 1){
break inner;
}
}
//If special location, count plus 1
count++;
}
}
}
return count;
}
}
7. 463. Perimeter of the island
1. Title
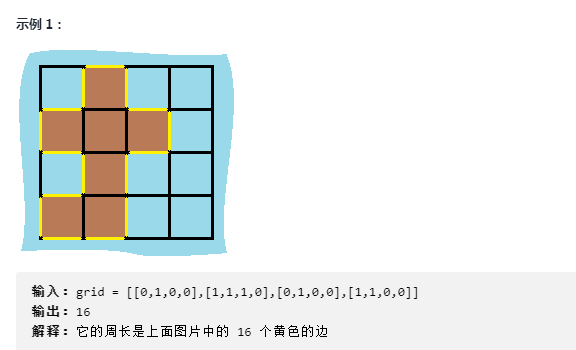
Given a two-dimensional grid map grid of row x col, where grid[i][j] = 1 represents land and grid[i][j] = 0 represents water.
The grids in the grid are connected horizontally and vertically (diagonally disconnected). The entire grid is completely surrounded by water, but there happens to be one of the islands (or one or more of the islands that are connected by grids representing land).
There is no lake on the island ("lake" means that the water is inside the island and not connected to the water around the island). The grid is a square with a side of 1. The grid is rectangular and has a width and height of no more than 100. Calculate the perimeter of the island.
2. Analysis
- Traverse first to find out the number of land blocks and the left and right duplicate boundaries of adjacent land.
- Traverse again to find the upper and lower duplicate boundaries of adjacent land.
- Last Return land land number amount ∗ 4 − heavy complex edge circles number amount Number of Land* 4 - Number of Duplicate Boundaries Number of Land 4 Number of Repeated Boundaries
3. Code
class Solution {
public int islandPerimeter(int[][] grid) {
int m = grid.length,n = grid[0].length;
//Number of Land Blocks
int count = 0;
//Number of edges to subtract
int line = 0;
for (int i = 0;i < m;i++){
for (int j = 0;j < n;j++){
if (grid[i][j] == 1){
count++;
if (j > 0 && grid[i][j - 1] == 1){
line += 2;
}
}
}
}
for (int j = 0;j < n;j++){
for (int i = 0;i < m;i++){
if (grid[i][j] == 1 && i > 0 && grid[i - 1][j] == 1){
line += 2;
}
}
}
return count * 4 - line;
}
}