
☘ preface ☘
Today is the seventh day of the nine day training. I will record the learning contents and problem solutions and strive to be the class representative 0.0
Link: LeetCode zero foundation guide (Lecture 8) two dimensional array
🧑🏻 About the author: a young man who changed from industrial design to embedded
✨ Contact: 2201891280(QQ)
⏳ Approximate reading time of the full text: 20min
🎁 Main knowledge points
📝 1. Definition of matrix
Matrix Amxn defines a set of negative or real numbers arranged according to a rectangular array, where n represents the number of rows and m represents the number of columns. The following figure shows a 4x3 matrix
A
4
x
3
=
[
0
1
0
0
0
1
1
0
0
1
0
0
]
A_{4x3} = \begin{bmatrix} 0&1&0 \\ 0&0&1\\ 1&0&0\\ 1&0&0 \end{bmatrix}
A4x3=⎣⎢⎢⎡001110000100⎦⎥⎥⎤
In c language, we can use two-dimensional array A[n][m] to represent an nxm matrix, where ` ` A[i][j] represents the elements in row I and column j.
🍭 2. Horizontal flip of matrix
The horizontal flip of a matrix is to reverse the order of the elements in each row of the matrix.
A
4
x
3
=
[
0
1
0
0
0
1
1
0
0
1
0
0
]
⟹
A
4
x
3
′
=
[
0
1
0
1
0
0
0
0
1
0
0
1
]
A_{4x3} = \begin{bmatrix} 0&1&0 \\ 0&0&1\\ 1&0&0\\ 1&0&0 \end{bmatrix} \Longrightarrow A^{'}_{4x3} = \begin{bmatrix} 0&1&0 \\ 1&0&0\\ 0&0&1\\ 0&0&1 \end{bmatrix}
A4x3=⎣⎢⎢⎡001110000100⎦⎥⎥⎤⟹A4x3′=⎣⎢⎢⎡010010000011⎦⎥⎥⎤
🍜 3. Vertical flip of matrix
The vertical flip of a matrix is to reverse the order of the elements in each column of the matrix.
A
4
x
3
=
[
0
1
0
0
0
1
1
0
0
1
0
0
]
⟹
A
4
x
3
′
′
=
[
1
0
0
1
0
0
0
0
1
0
1
0
]
A_{4x3} = \begin{bmatrix} 0&1&0 \\ 0&0&1\\ 1&0&0\\ 1&0&0 \end{bmatrix} \Longrightarrow A^{''}_{4x3} = \begin{bmatrix} 1&0&0 \\ 1&0&0\\ 0&0&1\\ 0&1&0 \end{bmatrix}
A4x3=⎣⎢⎢⎡001110000100⎦⎥⎥⎤⟹A4x3′′=⎣⎢⎢⎡110000010010⎦⎥⎥⎤
🍡 4. Clockwise rotation of matrix
The clockwise rotation of the matrix 90 degrees, as the name suggests, is 90 degrees around the direction perpendicular to the screen.
A
4
x
3
=
[
0
1
0
0
0
1
1
0
0
1
0
0
]
⟹
A
3
x
4
′
′
′
=
[
1
1
0
0
0
0
0
1
0
0
1
0
]
A_{4x3} = \begin{bmatrix} 0&1&0 \\ 0&0&1\\ 1&0&0\\ 1&0&0 \end{bmatrix} \Longrightarrow A^{'''}_{3x4} = \begin{bmatrix} 1&1&0&0\\ 0&0&0&1\\ 0&0&1&0\\ \end{bmatrix}
A4x3=⎣⎢⎢⎡001110000100⎦⎥⎥⎤⟹A3x4′′′=⎣⎡100100001010⎦⎤
🍛 5. Counterclockwise rotation of matrix
Turning 90 degrees counterclockwise is 270 degrees clockwise.
🍣 6. Counterclockwise transpose of matrix
Is to exchange the diagonals of the matrix.
A
4
x
3
=
[
0
1
0
0
0
1
1
0
0
1
0
0
]
⟹
A
3
x
4
T
=
[
0
0
1
1
1
0
0
0
0
1
0
0
]
A_{4x3} = \begin{bmatrix} 0&1&0 \\ 0&0&1\\ 1&0&0\\ 1&0&0 \end{bmatrix} \Longrightarrow A^{T}_{3x4} = \begin{bmatrix} 0&0&1&1\\ 1&0&0&0\\ 0&1&0&0\\ \end{bmatrix}
A4x3=⎣⎢⎢⎡001110000100⎦⎥⎥⎤⟹A3x4T=⎣⎡010001100100⎦⎤
🍢 7. Function transfer parameters of two-dimensional array
int diagonalSum(int** mat, int matSize, int* matColSize){
}
The first matSize represents the number of rows, while matColSize represents the number of elements per row. So it's an array. matColSize[0] is the number of elements in line 0.
General writing:
int diagonalSum(int** mat, int matSize, int* matColSize){
r = matSize;
c = matColSize[0];
// TODO
}
🍗 After class exercises
1351. Negative numbers in statistically ordered matrices
1351. Negative numbers in statistically ordered matrices
Title Description
Give you a matrix grid of m * n. The Elements in the matrix are arranged in non increasing order, whether in rows or columns.
Please count and return the number of negative numbers in the grid.
thinking
Use bisection to find the first negative element. At the same time, because the column is also non incremental, the value of high does not need to be modified every time, but only lower the low.
int countNegatives(int** grid, int gridSize, int* gridColSize){
int low = 0,high = gridColSize[0],ans= 0;
for(int i = 0;i < gridSize;i++){
low = 0;
while(low<high){
int mid = (low + high) /2;
if(grid[i][mid] >= 0) low = mid + 1;
else high = mid;
}
ans += gridColSize[i] - high;
}
return ans;
}
1572. Sum of diagonal elements of matrix
1572. Sum of diagonal elements of matrix
Title Description
Give you a square matrix mat, please return the sum of the diagonal elements of the matrix.
Please return the sum of the elements on the main diagonal and the elements on the sub diagonal and not on the main diagonal of the matrix.
thinking
Just scan down from the first line. But note that when the length is odd, it will be added in the middle, but even numbers will not!
int diagonalSum(int** mat, int matSize, int* matColSize){
int ans = 0;
for(int i = 0;i < matSize;i++)
ans += mat[i][i] + mat[i][matSize - 1 - i];
if(matSize & 1) ans -= mat[matSize/2][matSize/2];
return ans;
}
1672. Total assets of the richest customers
1672. Total assets of the richest customers
Title Description
Give you an integer grid accounts of m x n, where accounts[i][j] is the number of assets hosted by the ith customer in the j bank. Returns the total amount of assets owned by the richest customer.
The total assets of customers are the sum of the assets they hold in each bank. The richest customer is the customer with the largest total assets.
thinking
Just scan the maximum value directly?
int maximumWealth(int** accounts, int accountsSize, int* accountsColSize){
int maxn = 0,temp;
for(int i = 0;i < accountsSize; ++i){
temp = 0;
for(int j = 0;j < *accountsColSize; ++j) temp += accounts[i][j];
if(temp > maxn) maxn = temp;
}
return maxn;
}
1672. 766. Toplitz matrix
Title Description
Give you a matrix of m x n. If the matrix is a toplitz matrix, return true; Otherwise, false is returned.
If the elements on each diagonal from top left to bottom right are the same, then the matrix is a toplitz matrix.
thinking
The prompt gives me a message. You can only read in one line at a time, so you can scan one line at a time and compare it with the elements in the previous line.
bool isToeplitzMatrix(int** matrix, int matrixSize, int* matrixColSize){
for(int i = 1;i < matrixSize;i++)
for(int j = 1;j<matrixColSize[0];j++)
if(matrix[i][j] != matrix[i-1][j-1]) return false;
return true;
}
1380. Lucky numbers in the matrix
1380. Lucky numbers in the matrix
Title Description
Give you a matrix of m * n, the numbers in the matrix are different. Please return all lucky numbers in the matrix in any order.
Lucky numbers refer to the elements in the matrix that meet the following two conditions at the same time:
- The smallest of all elements in the same row
- Maximum of all elements in the same column
thinking
According to the maximum value of each row of elements to see if it is the maximum value of a column?
int* luckyNumbers (int** matrix, int matrixSize, int* matrixColSize, int* returnSize){
int *ans = malloc(sizeof(int)*matrixSize),ansnum = 0;
for(int i = 0;i < matrixSize;i++){
int min = matrix[i][0],minj = 0;
for(int j = 1;j < matrixColSize[0];j++)
if(matrix[i][j] < min) min = matrix[i][j],minj = j;
int k = 0;
for(;k < matrixSize;k++)
if(matrix[k][minj] > min) break;
if(k == matrixSize)
ans[ansnum++] = min;
}
*returnSize = ansnum;
return ans;
}
1582. Special positions in binary matrix
1582. Special positions in binary matrix
Title Description
A two-dimensional grid map grid of row x col is given, where grid[i][j] = 1 represents land and grid[i][j] = 0 represents water.
The grids in the grid are connected horizontally and vertically (not diagonally). The whole grid is completely surrounded by water, but there is exactly one island (or an island composed of one or more grids representing land).
There is no "Lake" in the island ("Lake" means that the water is inside the island and not connected with the water around the island). The grid is a square with side length of 1. The grid is rectangular and its width and height do not exceed 100. Calculate the perimeter of the island.
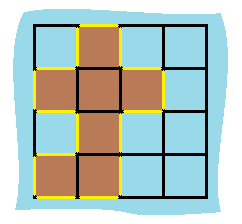
thinking
Scan each grid. If there is no block around, it is 4 sides, and if there is one, it is 3. Decrease in turn.
int numSpecial(int** mat, int matSize, int* matColSize){
int ans = 0;
int hash[*matColSize];
for(int j = 0; j < *matColSize; ++j){
hash[j] = 0;
for(int i = 0;i <matSize;i++)
if(mat[i][j] == 1) hash[j] ++;
}
for(int i = 0;i < matSize; ++i){
int temp = 0,tempi = -1;
for(int j = 0; j < *matColSize; ++j)
if(mat[i][j] == 1) temp++,tempi = j;
if(temp == 1)
if(hash[tempi] == 1) ans++;
}
return ans;
}
463. Perimeter of the island
Title Description
Give you a matrix mat with the size of rows x cols, where mat[i][j] is 0 or 1. Please return the number of special positions in the matrix mat.
Special position definition: if mat[i][j] == 1 and all other elements in row I and column j are 0 (the subscripts of rows and columns start from 0), the position (i, j) is called a special position.
thinking
The prompt gives me a message. You can only read in one line at a time, so you can scan one line at a time and compare it with the elements in the previous line.
int islandPerimeter(int** grid, int gridSize, int* gridColSize){
int ans = 0;
for(int i = 0;i < gridSize;i++)
for(int j = 0;j < gridColSize[0];j++)
if(grid[i][j] == 1){
int temp = 4;
if(i > 0 && grid[i-1][j]) temp--;
if(i < (gridSize - 1) && grid[i+1][j]) temp--;
if(j > 0 && grid[i][j-1]) temp--;
if(j < (gridColSize[0] - 1) && grid[i][j+1]) temp--;
ans+=temp;
}
return ans;
}
📑 Write at the end
Today, I completed the clock out for the seventh day. Recently, I was dominated by level 6. I want to pigeon for a few days. Is that ok. Only when necessary, it will be updated. It takes at least four hours to punch in custom every day. It's too long. I'm sure to update it after Passing CET6 --