The maximum rectangular area of rainwater and histogram are two problems that echo each other. There are many similarities in principle, but there are differences in details.
Connected to rainwater (monotonous stack)
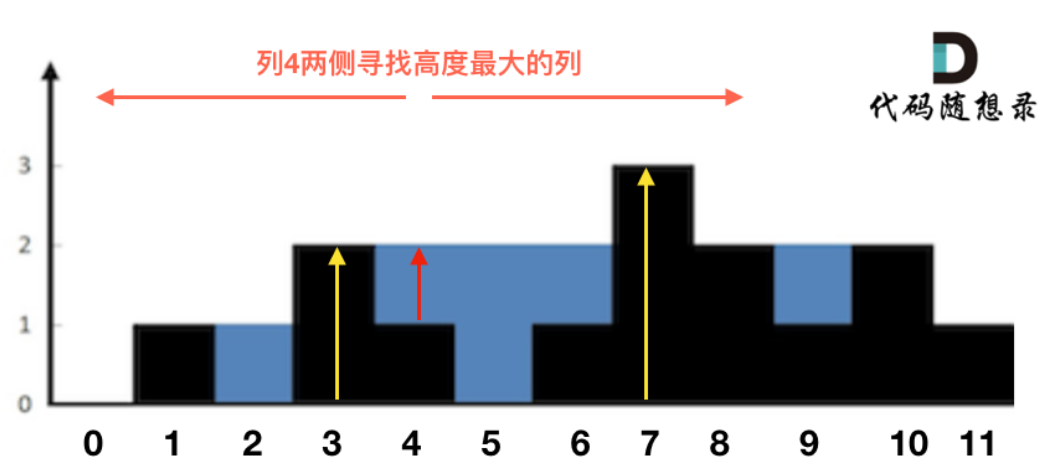
Brute force method (double pointer):
Note that after finding the highest column on the left and right sides, it is also necessary to judge whether the height is greater than the height of column i (so as to "store water"), and the total amount of rainwater can be added only when the conditions are met.
public int trap_ShuangZhiZhen(int[] heights) {
int waterSum = 0;
for(int i=1; i<heights.length-1; i++) {
int left = i-1;
int right = i+1;
// Use double pointers to find the highest on the left and right sides respectively
int left_height = heights[i-1];
int right_height = heights[i+1];
while (left > 0) {
left--;
left_height = Math.max(heights[left], left_height);
}
while (right < heights.length-1) {
right++;
right_height = Math.max(heights[right], right_height);
}
// It is also necessary to judge whether the height is greater than the height of column i (so as to "store water"), and the total amount of rainwater can be added only when the conditions are met
if(left_height > heights[i] && right_height > heights[i]){
waterSum += Math.min(left_height, right_height) - heights[i];
}
}
return waterSum;
}
Dynamic planning:
In the double pointer solution, we can see that as long as the maximum height of the left column and the maximum height of the right column are recorded, the rainwater area at the current position can be calculated through the column.
Rainwater area of current column: min (maximum height of left column, record the maximum height of right column) - current column height.
In order to get the highest height on both sides, double pointers are used to traverse. Each column is traversed to both sides. In fact, there is repeated calculation. We record the maximum height on the left of each position in an array (maxLeft) and the maximum height on the right in an array (maxRight). This avoids repeated calculation, which uses dynamic programming.
In the current position, the highest height on the left is the highest height on the left of the previous position and the maximum value of this height.
That is, traverse from left to right: maxLeft[i] = max(height[i], maxLeft[i - 1]);
Traverse from right to left: maxRight[i] = max(height[i], maxRight[i + 1]);
Monotone stack:
The order from the top of the stack (elements pop up from the top of the stack) to the bottom of the stack should be from small to large.
main points:
- From the bottom of the stack to the top of the stack is decreasing.
- Brute force double pointer solution ponding is vertical, monotone stack solution ponding is horizontal! Pay attention to the difference!!
public int trap(int[] heights) {
Stack<Integer> stack = new Stack<>();
int waterSum = 0;
stack.push(0);
for(int i=1; i<heights.length; i++){
if(heights[i] <= heights[stack.peek()]){
stack.push(i);
}else {
while (!stack.empty() && heights[i] > heights[stack.peek()]){
int pop_id = stack.pop();
int pop_height = heights[pop_id];
// Unlike the largest rectangle, you can use 0 as a sentry, because it is decreasing. To set a sentry, you need to set a large number, which is not easy to determine.
if (!stack.empty()){
int height = Math.min(heights[i], heights[stack.peek()]) - pop_height;
int width = i - stack.peek() - 1;
waterSum += height * width;
}
}
stack.push(i);
}
}
return waterSum;
}
Maximum rectangular area of histogram
See the special Offer, code Capriccio and explanation at station B (better)
Brute force method:
It is also divided into double pointer brute force and brute force in the book.
Double pointer is to find a rectangle whose front and rear height is less than its own, which is more in line with the conventional idea. But the time complexity is n ².
public int largestRectangleArea_ShuangZhiZhen(int[] heights){
// Add sentinels at the beginning and end to simplify the code (remove empty judgment)
int[] new_heights = new int[heights.length+2];
for(int i=0; i<heights.length; i++){
new_heights[i+1] = heights[i];
}
heights = new_heights;
int maxArea = 0;
for(int i=1; i<new_heights.length; i++){
// Double pointer look back and forth
int left = i;
int right = i;
while (left>0 && heights[left] >= heights[i]){
left--;
}
while (right<heights.length && heights[right] >= heights[i]){
right++;
}
int width = right - left - 1;
int area = width * heights[i];
maxArea = Math.max(area, maxArea);
}
return maxArea;
}
Divide and Conquer:
The loop termination condition is written in front
Divide left and right, pay attention to the dividing point
Monotone stack:
(dual to the question of receiving rainwater) the monotonic stack receiving rainwater decreases from the bottom of the stack to the top of the stack, and here the monotonic stack increases from the bottom of the stack to the top of the stack. Receiving rainwater is to find concave, here is to find convex. What is stored in the monotonic stack is subscript.
The largest rectangle with a column as the top must extend from the column to both sides until it meets a column lower than it. The height of the largest rectangle is the height of the column, and the width of the largest rectangle is the spacing between the columns lower than it on both sides.
If the height of the currently scanned column is less than that of the column at the top of the stack, the subscript of the column at the top of the stack is marked out of the stack, and the maximum rectangular area with the column at the top of the stack as the top is calculated. Since the height of the columns stored in the stack is sorted incrementally, the column in front of the top of the stack must be lower than the column at the top of the stack, so it is easy to find the columns lower on both sides of the column at the top of the stack.
Key points of monotone stack solution:
- The stack increases from the bottom of the stack to the top of the stack (including the special case of adjacent equal height)
- The subscript is stored in the stack, which is very important. When calculating the width of the maximum rectangle at the top of the stack, the width = the element to be put into the stack - the next element of the element at the top of the stack - 1 (the next element of the element at the top of the stack and the element to be put into the stack will pop up the maximum rectangle width of the element on the stack)
- Add two sentinels with height of 0 to the first place of the original height sequence to avoid the judgment that the stack is empty and to avoid discussing the situation that there are a few elements left in the last stack.
code:
public int largestRectangleArea_DanDiaoZhan(int[] heights){
Stack<Integer> stack = new Stack<>();
// Add sentry!! Simplify the main code, avoid the judgment that the stack is empty, and avoid discussing the situation that there are a few elements left in the last stack
int[] new_heights = new int[heights.length + 2];
for(int i=0; i<heights.length; i++){
new_heights[i+1] = heights[i];
}
heights = new_heights;
int maxArea = 0;
stack.push(0);
for(int i=1; i<heights.length; i++){
if(heights[i] >= heights[stack.peek()]){
stack.push(i);
continue;
}else {
// In order to ensure the increment of the stack, you can always bounce the stack when you encounter a small one
while (heights[i] < heights[stack.peek()]){
int height = heights[stack.pop()];
// Special case of determining equal height
while(height == heights[stack.peek()]){
stack.pop();
}
int width = i - stack.peek() - 1;
int area = width * height;
maxArea = Math.max(area, maxArea);
}
stack.push(i);
}
}
return maxArea;
}