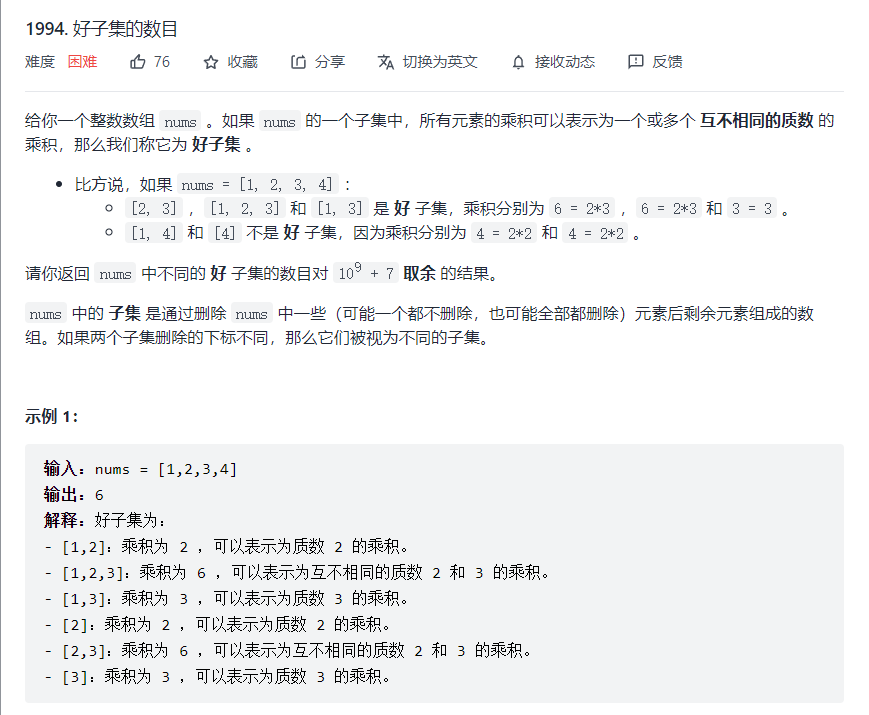
the data range of this question is relatively small, which determines that state compression dp can be used.
to split the product of all numbers in the subset into different prime factors, the subset must hold different prime factors, and each element subset cannot hold duplicate prime factors.
since the data range is 1 ~ 30, there are only 10 prime numbers in total. We can use a binary string with length of 10 to represent the prime factor held by each number in our subset.
then consider defining the state as
f
(
i
,
m
a
s
k
)
f(i, mask)
f(i,mask) represents the number of 2~i, and the quality factor distribution of the subset is
m
a
s
k
mask
The total number of subset schemes of the mask.
if the number i currently traversed does not exist in the array, it cannot be transferred;
if the number i currently traversed holds repeated prime factors, it is impossible to select the current number into the subset, and the state transition equation is
f
[
i
]
[
m
a
s
k
]
=
f
[
i
−
1
]
[
m
a
s
k
]
f[i][mask] = f[i - 1][mask]
f[i][mask]=f[i−1][mask];
if the number currently traversed does not hold duplicate prime factors, let the holding of the current number prime factor be
s
u
b
s
e
t
subset
Subset, you can select the current number into the subset, including
c
n
t
[
i
]
cnt[i]
cnt[i] current number I, then there is
c
n
t
[
i
]
cnt[i]
cnt[i] can be selected or not. The state transition equation is:
f
[
i
]
[
m
a
s
k
]
=
f
[
i
−
1
]
[
m
a
s
k
]
+
c
n
t
[
i
]
∗
f
[
i
−
1
]
[
m
a
s
k
s
u
b
s
e
t
]
,
i
f
(
(
m
a
s
k
&
s
u
b
s
e
t
)
=
=
s
u
b
s
e
t
)
f[i][mask] = f[i - 1][mask] + cnt[i] * f[i - 1][mask subset],if ((mask \& subset) == subset)
f[i][mask]=f[i−1][mask]+cnt[i]∗f[i−1][masksubset],if((mask&subset)==subset)
here, XOR is used to eliminate the same bit and keep different bits as 1. Only the quality factor distribution of i is included in the quality factor distribution currently considered, which corresponds to the binary bit,
s
u
b
s
e
t
subset
subset must be
m
a
s
k
mask
A subset of the mask.
class Solution {
public:
int prime[10] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29};
static const int N = 1e9 + 7;
int numberOfGoodSubsets(vector<int>& nums)
{
// First look at the data range 1 < = nums [i] < = 30. There are only these prime numbers in the range 1 ~ 30:
// 2 3 5 7 11 13 17 19 23 29 10 in total
// This problem requires that the product be divided into the product of one or more different quality factors
// We can use a 10 bit binary number mask to indicate whether each quality factor has been selected
// Definition f[i][mask] indicates the total number of schemes considered in the range of 2~i when the quality factor selection is mask
// The answer is to sum f[30][k] k from 1 to 1 < < 10 indicates the selection of all prime numbers
// State transition equation: if I contains multiple identical quality factors, I equation cannot be selected as f[i][mask] = f[i - 1][mask]
// If i contains multiple different quality factors, remember that their quality factor distribution is subset (a 10 bit binary number)
// If the subset is a subset of the mask, that is, Mask & subset = = subset, it can be transferred
// The state transition equation is f[i][mask] = f[i - 1][mask] + f[i - 1][mask ^ subset] * cnt[i]
// You can choose cnt[i] as an I, so you have to multiply cnt[i]
// XOR changes the same all to 0 and the different all to 1
// Initial condition f[1][0] = 2^(cnt[1]), because each 1 can be selected or not, and 2^(cnt[1]) cases are added
vector<int> cnt(31);
// count
for (auto l : nums)
{
++cnt[l];
}
int mask_max = 1 << 10;
// Considering that the array of state transition is only related to the predecessor, it is optimized with a one-dimensional array
vector<int> dp(mask_max);
// initial condition
dp[0] = 1;// First initialize to 1, where dp[0] is f[1][0]
// Whether there is 1 or not, we can assume that there is 1, which does not affect the multiplication count
// Then maintain dp[0] as 2^(cnt[1])
for (int i = 0; i < cnt[1]; ++i)
{
dp[0] = dp[0] * 2 % N;
}
for (int i = 2; i <= 30; ++i)
{
// If there is no element in the array, there is no need to select it
if (!cnt[i]) continue;
// See if it holds repeated quality factors, and count the occurrence of other quality factors
int x = i, subset = 0;
bool flag = true;
for (int j = 0; j < 10; ++j)
{
if (x % (prime[j] * prime[j]) == 0)
{
flag = false;
break;
}
if (x % prime[j] == 0)
{
subset |= (1 << j);
}
}
// If you hold the repeated prime factor, you don't consider this number
if (flag == false)
{
continue;
}
// Otherwise, carry out dynamic planning
// Because subset is a subset of mask, subset ^ mask must be smaller than mask
// Therefore, the dynamic programming optimization of one-dimensional array is to ensure the calculation to dp[mask ^ subset]
// It is also the f[i - 1][mask ^ subset] of the previous layer, so the loop starts from the mask_max - 1 go small
for (int mask = mask_max - 1; mask > 0; --mask)
{
if ((subset & mask) == subset)
{
dp[mask] =
(dp[mask] + static_cast<long long>(dp[mask ^ subset]) * cnt[i]) % N;
}
}
}
int ret = 0;
for (int mask = 1; mask < mask_max; ++mask)
{
ret = (ret + dp[mask]) % N;
}
return ret;
}
};
this topic can also be pruned. It is impossible to insert the neutron concentration of this topic 4 , 8 , 9 , 12 , 16 , 18 , 20 , 24 , 25 , 27 , 28 4,8,9,12, 16, 18, 20, 24, 25, 27, 28 4. 8, 9, 12, 16, 18, 20, 24, 25, 27, 28 because they all contain the square of prime numbers 2 ∗ 2 2*2 2 * 2 or 3 ∗ 3 3*3 3 * 3 or 5 ∗ 5 5*5 5 * 5, use a hash table to store these numbers in advance, if hash count(i) != 0 just continue.
class Solution {
public:
int prime[10] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29};
int mask_max = (1 << 10) - 1;
unordered_set<int> hash = {4, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28};
static const int N = 1e9 + 7;
int numberOfGoodSubsets(vector<int>& nums)
{
vector<int> cnt(31);
for (int num : nums){
++cnt[num];
}
vector<int> dp(mask_max + 1);
dp[0] = 1;
for (int i = 0; i < cnt[1]; ++i)
{
dp[0] = dp[0] * 2 % N;
}
for (int i = 2; i <= 30; ++i)
{
if (cnt[i] == 0 || hash.count(i) != 0) continue;
int x = i, subset = 0;
bool flag = true;
for (int j = 0; j < 10; ++j)
{
if (x % (prime[j] * prime[j]) == 0){
flag = false;
break;
}
if ((x % prime[j]) == 0)
{
subset |= (1 << j);
}
}
if (flag == false) continue;
for (int mask = mask_max; mask > 0; --mask)
{
if ((mask & subset) == subset)
{
dp[mask] =
(dp[mask] + static_cast<long long>(dp[mask ^ subset]) * cnt[i]) % N;
}
}
}
int ret = 0;
for (int mask = 1; mask <= mask_max; ++mask)
{
ret = (ret + dp[mask]) % N;
}
return ret;
}
};