Plates between candles
Here is a long table with plates and candles lined up on it. Give you a string s with subscript starting from 0. It only contains the characters' * 'and' | ', where' * 'represents a plate and' | 'represents a candle.
At the same time, give you a two-dimensional integer array queries with subscript starting from 0, where queries[i] = [lefti, righti] represents the substring s[lefti...righti] (including the characters of the left and right endpoints). For each query, you need to find the number of plates between two candles in the substring. If a plate has at least one candle on the left and right of the substring, the plate is satisfied between the two candles.
- For example, s = "|*************", query [3, 8], which represents the substring "* |*********************************************************************. The number of plates between two candles in the substring is 2, and the two plates on the right in the substring have at least one candle on their left and right.
Please return an integer array answer, where answer[i] is the answer to the ith query.
Example 1:
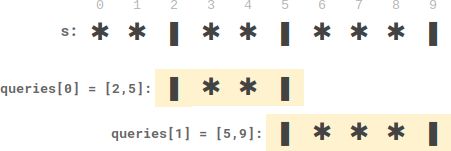
Input: s = "**|**|***|", queries = [[2,5],[5,9]] Output:[2,3] Explanation: - queries[0] There are two plates between the candles. - queries[1] There are three plates between the candles.
Example 2:
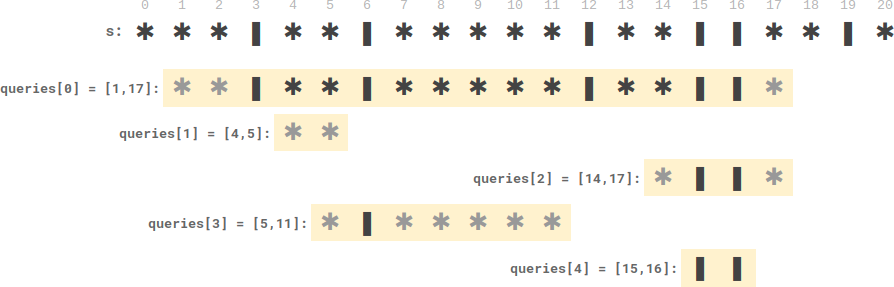
Input: s = "***|**|*****|**||**|*", queries = [[1,17],[4,5],[14,17],[5,11],[15,16]] Output:[9,0,0,0,0] Explanation: - queries[0] There are nine plates between the candles. - Another query has no plates between candles.
Tips:
- 3 <= s.length <= 105
- s contains only the characters' * 'and' | '.
- 1 <= queries.length <= 105
- queries[i].length == 2
- 0 <= lefti <= righti < s.length
solution
This problem is mainly the prefix and to save the number of plates, and then record the position of candles.
class Solution {
public:
vector<int> platesBetweenCandles(string s, vector<vector<int>>& queries) {
int n = s.length();
vector<int> preSum(n);
for (int i = 0, sum = 0; i < n; i++) {
if (s[i] == '*') {
sum++;
}
preSum[i] = sum;
}
vector<int> left(n);
for (int i = 0, l = -1; i < n; i++) {
if (s[i] == '|') {
l = i;
}
left[i] = l;
}
vector<int> right(n);
for (int i = n - 1, r = -1; i >= 0; i--) {
if (s[i] == '|') {
r = i;
}
right[i] = r;
}
vector<int> ans;
for (auto& query : queries) {
int x = right[query[0]], y = left[query[1]];
ans.push_back(x == -1 || y == -1 || x >= y ? 0 : preSum[y] - preSum[x]);
}
return ans;
}
};
Fill in the next right node pointer II of each node
Given a binary tree
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
Fill in each of its next pointers so that this pointer points to its next right node. If the next right node cannot be found, set the next pointer to NULL.
In the initial state, all next pointers are set to NULL.
Advanced:
- You can only use constant level extra space.
- Using recursion to solve the problem also meets the requirements. The stack space occupied by the recursive program in this problem is not considered as additional space complexity.
Example:
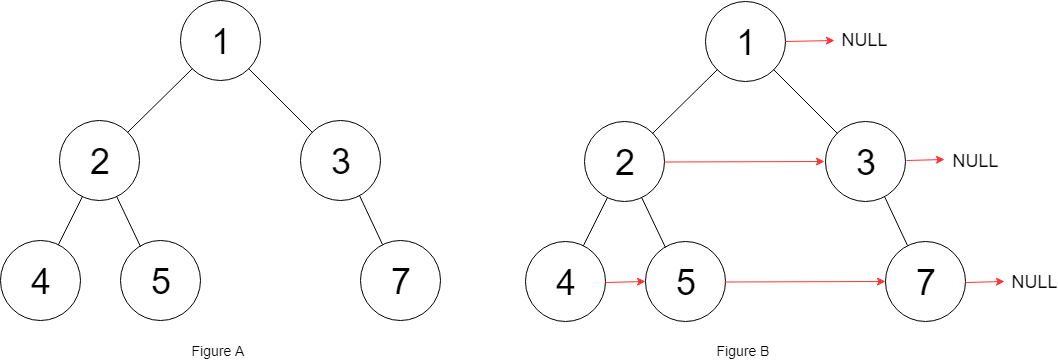
Input: root = [1,2,3,4,5,null,7] Output:[1,#,2,3,#,4,5,7,#] Explanation: the given binary tree is shown in the figure A As shown in, your function should fill each of it next Pointer to point to its next right node, as shown in the figure B As shown in. The serialized output is in sequence traversal order (by next Pointer connection),'#'indicates the end of each layer.
Tips:
- The number of nodes in the tree is less than 6000
- -100 <= node.val <= 100
solution
A question about bfs
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
if (!root) {
return nullptr;
}
queue<Node*> q;
q.push(root);
while (!q.empty()) {
int n = q.size();
Node *last = nullptr;
for (int i = 1; i <= n; ++i) {
Node *f = q.front();
q.pop();
if (f->left) {
q.push(f->left);
}
if (f->right) {
q.push(f->right);
}
if (i != 1) {
last->next = f;
}
last = f;
}
}
return root;
}
};
A subtree of another tree
Here are two binary trees, root and subRoot. Check whether the root contains subtrees with the same structure and node values as the subRoot. If it exists, return true; Otherwise, false is returned.
A subtree of a binary tree tree includes a node of the tree and all descendants of this node. A tree can also be regarded as a subtree of its own.
Example 1:
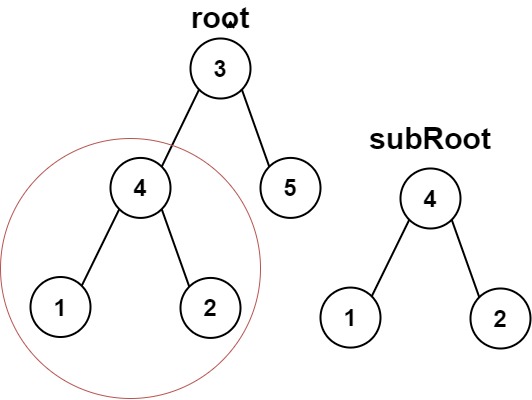
Input: root = [3,4,5,1,2], subRoot = [4,1,2] Output: true
Example 2:
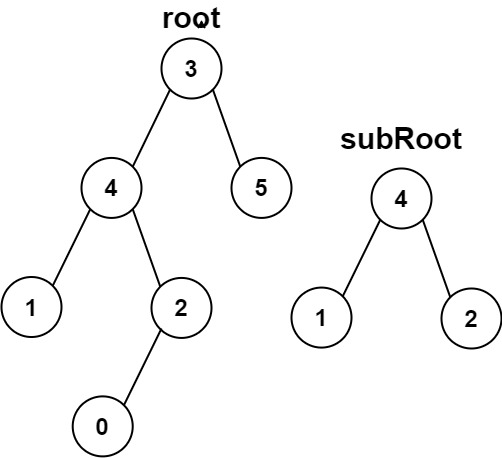
Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] Output: false
Tips:
- The number of nodes in the root tree ranges from [1, 2000]
- The number of nodes on the subRoot tree ranges from [1, 1000]
- -104 <= root.val <= 104
- -104 <= subRoot.val <= 104
solution
Fortunately, I learned the data structure, otherwise I had to g.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSametree(struct TreeNode* s, struct TreeNode* t)
{
if (s == NULL && t == NULL) return true;
return s && t
&& s->val == t->val
&& isSametree(s->left, t->left)
&& isSametree(s->right, t->right);
}
bool isSubtree(struct TreeNode* s, struct TreeNode* t) {
if (s == NULL && t == NULL) return true;
if (s == NULL && t != NULL) return false;
return isSametree(s, t)
|| isSubtree(s->left, t)
|| isSubtree(s->right, t);
}
};
L1-071 previous life files (20 points)

This kind of funny fortune telling applet is often encountered in the online world. The implementation principle is very simple. Design a few questions casually, and select a path in the judgment tree according to the player's answer to each question (as shown in the figure below). The conclusion is the node corresponding to the end of the path.
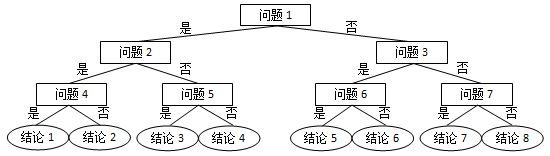
Now let's number the conclusions from left to right, starting with 1. Here, it is assumed that the answers are simple "yes" or "no", and that the answer "yes" corresponds to the left path, and the answer "no" corresponds to the right path. Given a series of answers from players, please return the number of their conclusions.
Input format:
Enter the first line and give two positive integers: N (≤ 30) is the number of questions to be answered by the player in a test; M (≤ 100) is the number of players.
Each player gives n answers in line. Here y stands for "yes" and N for "no".
Output format:
For each player, output the number of its corresponding conclusion in one line.
Input sample:
3 4 yny nyy nyn yyn
Output example:
3 5 6 2
solution
At the beginning, I thought this problem was particularly difficult, because I really gave up when I did this problem for the first time and added various cyclic judgments. When I did it today, I found that this is a problem of finding rules.
#include<bits/stdc++.h>
using namespace std;
int main() {
int n, m;
char c;
cin >> n >> m;
for(int i=0; i<m; i++) {
int cld = 1;
for(int j=1; j<=n; j++) {
cin >> c;
//If y, keep the current cld unchanged
//If it is n, calculate the value of the next y and assign it to cld
if(c == 'y')
cld += 0;
if(c == 'n')
cld += pow(2,n-j);
}
cout << cld << endl;
}
return 0;
}