Li Kou daily question 20207

Topic description

If the string does not contain any strings such as' aaa ',' bbb 'or' ccc 'as substrings, the string is a "happy string".

Here are three integers a, b and c. please return any string s that meets all the following conditions:

s is a happy string as long as possible. There are at most a letter 'a', b letter 'B', and c letter 'c' in s. s contains only
'a', 'b' and 'c'. If such a string s does not exist, return an empty string
Where 0 < = a, B, C < = 100
a + b + c > 0"".

Link: Force buckle 1405 Longest happy string

Solution: according to the meaning of this question, it is easy to think of the depth first search algorithm, namely dfs + pruning. At this time, the time complexity of the algorithm should be O (3^max(a,b,c)). Unfortunately, due to the range of parameters a, b and C, the execution time of the algorithm is slow, resulting in the final result of TLE.
The code is:

class Solution {
public:
    string ans;
    int Max;
    string x;
    int num[3];
    string longestDiverseString(int a, int b, int c) {
        map<char, int> s;
        s['a'] = 1;
        s['b'] = 1;
        s['c'] = 1;
        Max = 0;
        ans = "";
        x = "";
        num[0] = a;
        num[1] = b; num[2] = c;
        getLong(s,-1);
        return ans;
    }

    void getLong(map<char, int> s,int alpha)
    {
        int i;
        if (s['a'] == 3)
        {
            if (Max < x.length())
            {
                Max = x.length()-1;
                ans = x.substr(0,x.length()-1);
            }
            return;
        }
        if (s['b'] == 3)
        {
            if (Max < x.length())
            {
                Max = x.length() - 1;
                ans = x.substr(0, x.length() - 1);
            }
            return;
        }
        if (s['c'] == 3)
        {
            if (Max < x.length())
            {
                Max = x.length() - 1;
                ans = x.substr(0, x.length() - 1);
            }
            return;
        }
        for (i = 0; i < 3; i++)
            if (num[i] != 0)
                break;
        if (i == 3) {
            Max = x.length();
            ans = x;
            return;
        }
        for (int i = 0; i < 3; i++)
        {
            if (num[i] > 0)
            {
                num[i]--;
                if (x.length() != 0 && x[x.length() - 1] - 'a' == i) 
                    s['a' + i]++;
                else if (x.length() != 0) {
                    s['a' + i] = 1;
                }
                x += 'a' + i;
                getLong(s,i);
                x = x.substr(0, x.length() - 1);
                if (x.length() != 0 && x[x.length() - 1] - 'a' == i)
                    s['a' + i]--;
                num[i]++;
            }
        }

    }
};

The implementation results are:

Finally found that this is not a dfs, but a greedy!!!
You can look at the conditions of this topic first:

1. The consecutive number of each letter cannot exceed 3;
2. The number of letters is limited

The final result is the longest string, so it is easy to think of greedy strategy:

Letters with less numbers are used as isolated letters, and letters with more numbers are prioritized; If the current number of letters exceeds 3, skip the current letter until the current letter that can be added is found; If you can't find the letters that can be added at present, exit.

The code is:

class Solution {
public:
    class mycomp2 {
    public:
        bool operator() (pair<char, int> a, pair<char, int> b) {
            return (a.second > b.second);
        }
    };
    string longestDiverseString(int a, int b, int c) {
        string ans;
        vector<pair<char, int>> s = { {'a',a},{'b',b},{'c',c} };
        while (1) {
            bool flag = false;
            sort(s.begin(), s.begin()+s.size(), mycomp2());
            for (vector<pair<char, int>>::iterator it = s.begin(); it != s.end(); it++) {
                int m = ans.size();
                char ch = (*it).first;
                int freq = (*it).second;
                if (freq <= 0)
                    break;
                if (m >= 2 && ans[m - 2] == ch && ans[m - 1] == ch)
                    continue;
                ans.push_back(ch);
                flag = 1;
                (*it).second--;
                break;
            }
            if (!flag)
                break;
        }
        return ans;
    }    
};

The final operation result is:

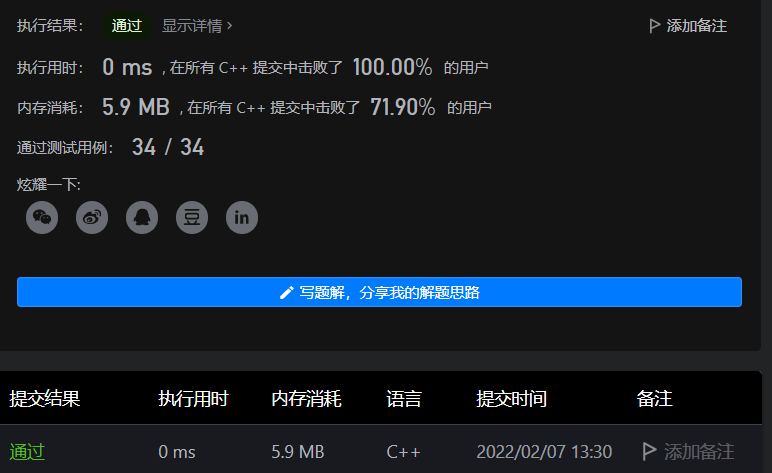
If greedy is adopted, the time complexity is greatly reduced. The main time is in sorting. If sort function is adopted, the time complexity is O((a+b+c) × ClogC).

Overview of this problem, found that the use of violence algorithm did not complete this problem well, it is easy to TLE; You still need to exercise your greed or dp logical thinking!