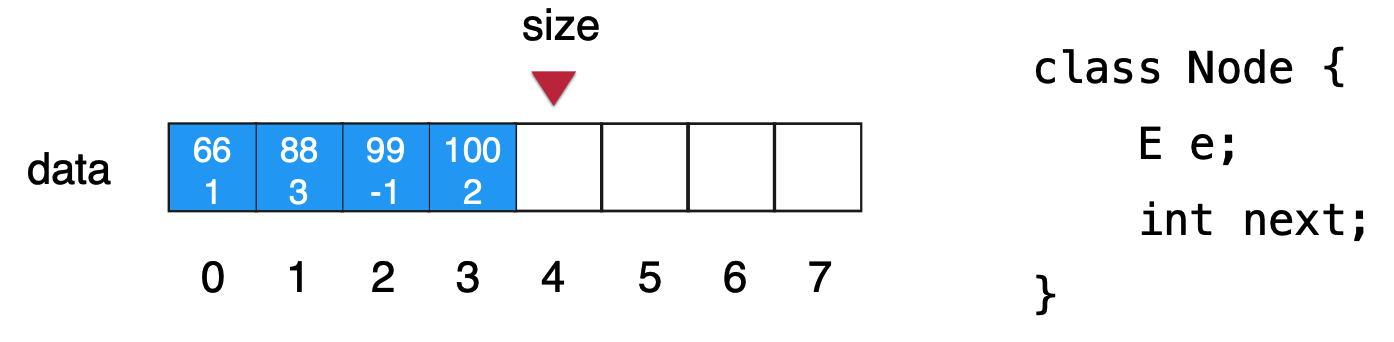
Linked list and recursion:
Last time https://www.cnblogs.com/webor2006/p/15575331.html We have made a preliminary study of recursion. At the end of the paper, it is mentioned that we must understand the macro semantics of recursion when writing the recursion algorithm, which will be much simpler. Many times, we can understand the recursion algorithm as a sub process. Here, we continue to further explore the relationship between linked list and recursion.
Natural recursion of linked list:
For the linked list, it is naturally recursive. How to understand it? For example, a linked list:

And it can actually imagine it like this:
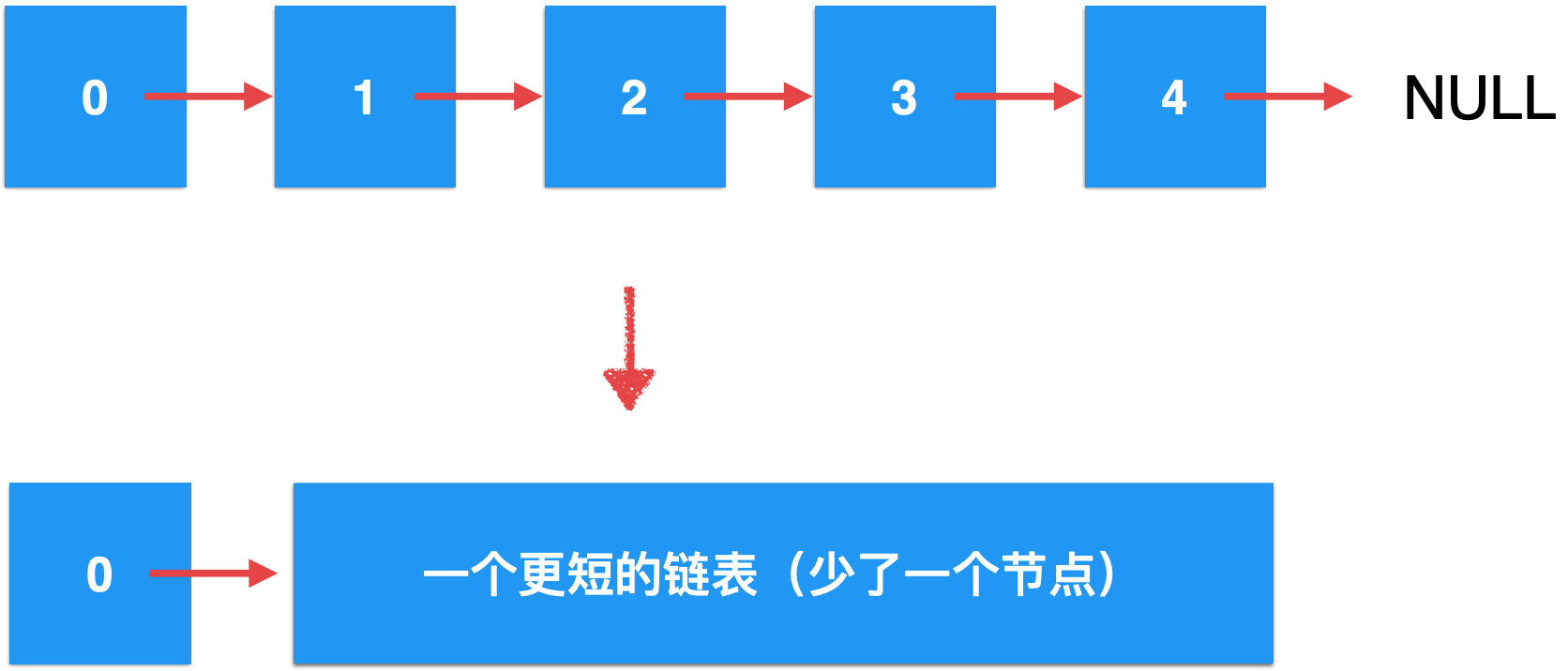
That is, a shorter linked list is hung behind the first element 0, which is the so-called "naturalness". For a linked list, we can understand it as the connection of nodes, or as a head node, and a smaller linked list is hung behind it. After thinking about this, In fact, many operations on the linked list can be completed by recursive logic, such as the following operation.
Solve the problem of deleting elements in the linked list:
Train of thought:
Take deleting the specified element in the linked list as an example. Two methods have been implemented last time:

However, neither of them is implemented by recursion. Next, we will use the idea of recursion to complete the same functions. First, let's sort out the idea [this overview is a little abstract, let's have a general understanding first], and first recall the methods defined for this problem:
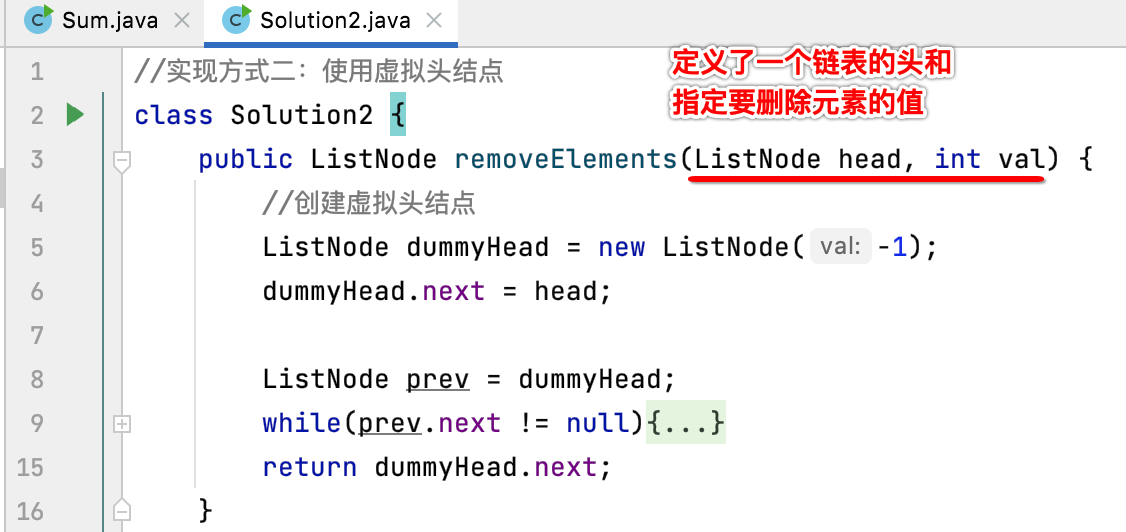
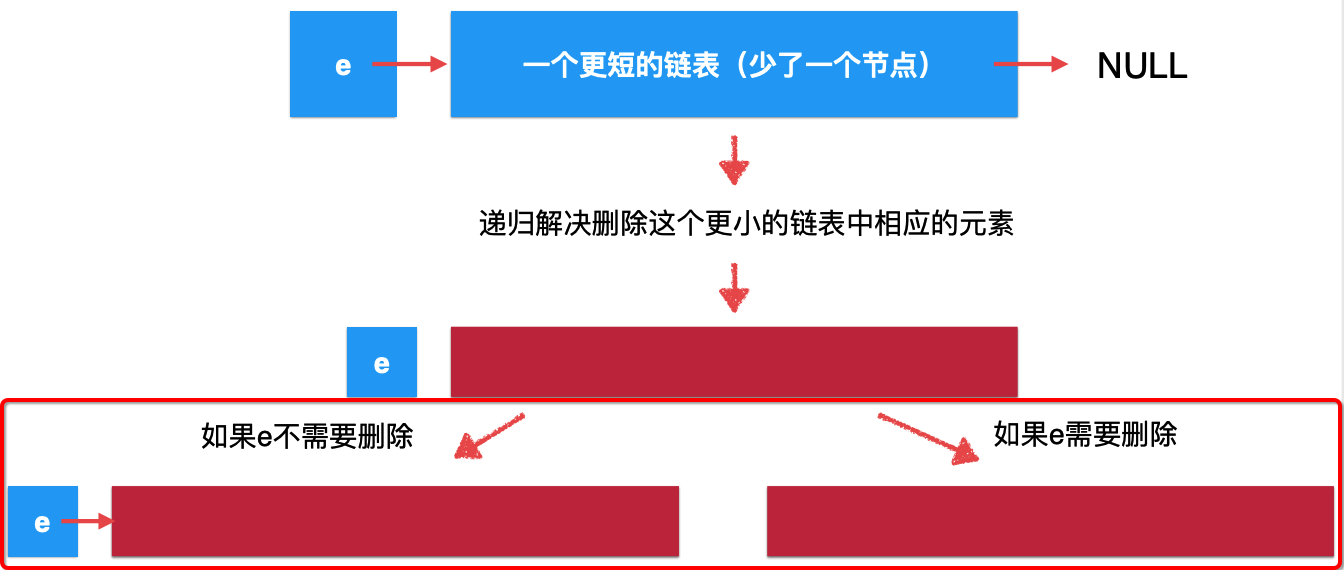
According to the natural recursion of the linked list, the original linked list can be understood as such a structure:

For this shorter linked list, through recursive function, from the macro semantic point of view, it becomes:
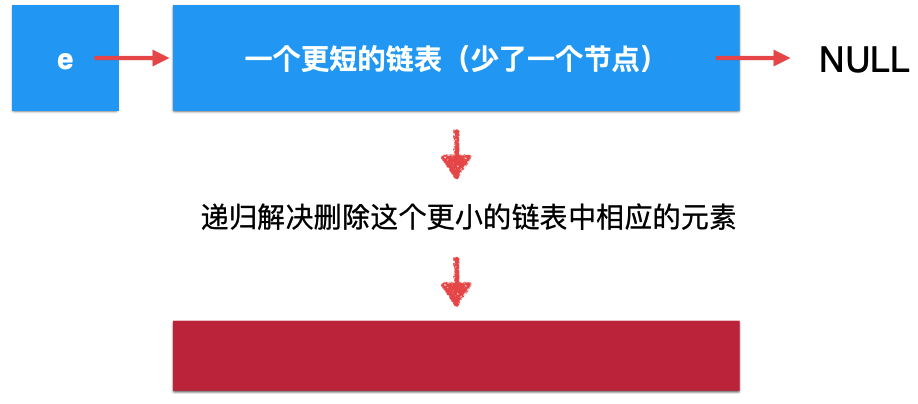
At present, it is not the solution of the original problem, because there is still one head node missing, so let's take the head node into account and it will be:
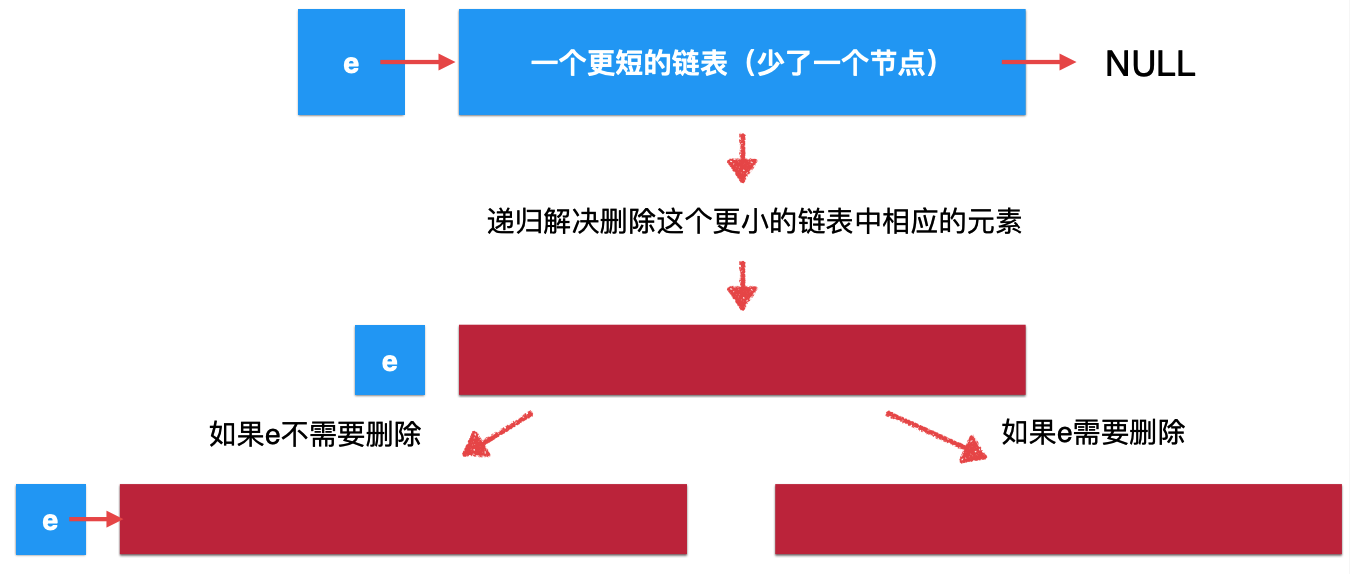
Is it more abstract? The idea of recursively deleting linked list elements can be further understood in combination with the specific code below.
realization:
1. New file:
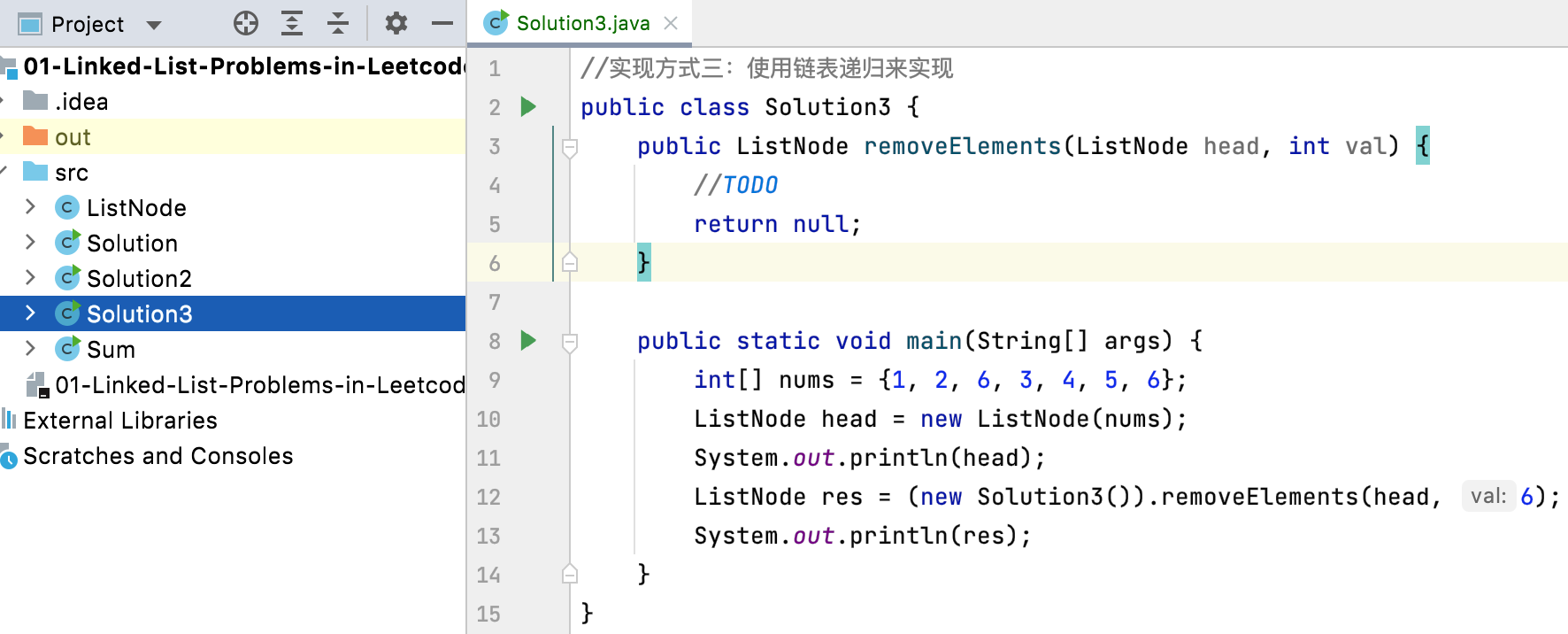
The template code is similar to that we implemented last time. Next, we will implement it with recursion. First, let's recall that there are two steps for a recursive implementation:
Therefore, the following is a recursive implementation according to this idea.
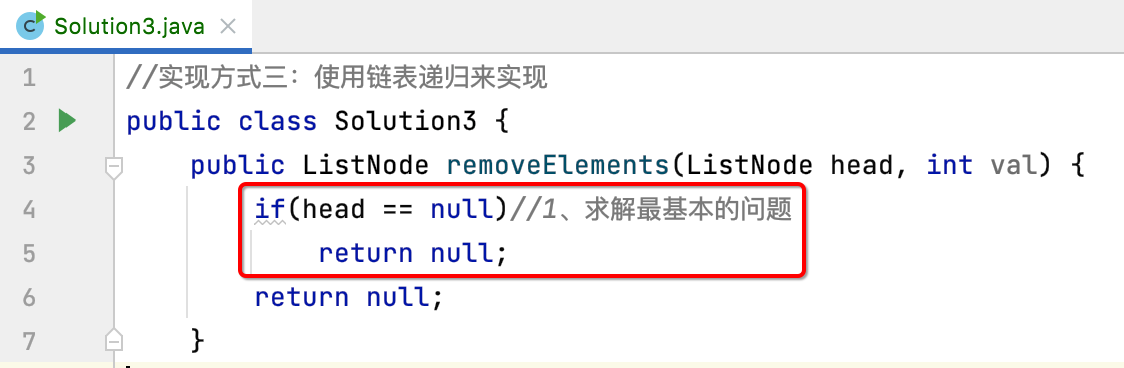
2. Solve the most basic problem:
In fact, first write the end condition of recursion. Obviously, when the smallest linked list of recursion is null, the whole recursion needs to end, so the code is as follows:
3. Turn the original problem into a smaller one:
Here is the key point of recursive implementation. Pay attention to the "macro" semantics to think about the preparation of this recursion. According to the above arrangement, first, it is necessary to call smaller linked lists to recursively delete elements: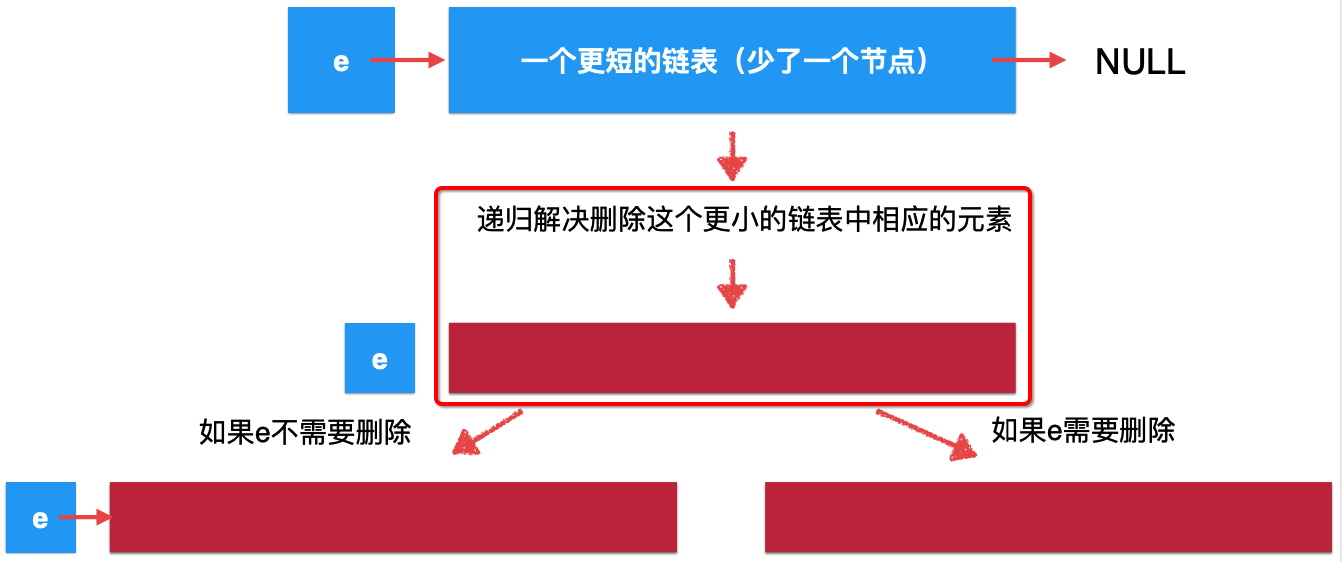
How to write it? The recursive routine is as follows:
Next, you need to deal with the header node:
This one is relatively simple, as follows:

That is to construct the original problem with the solution of a smaller problem.
4. Test:

There's something wrong with the wood.
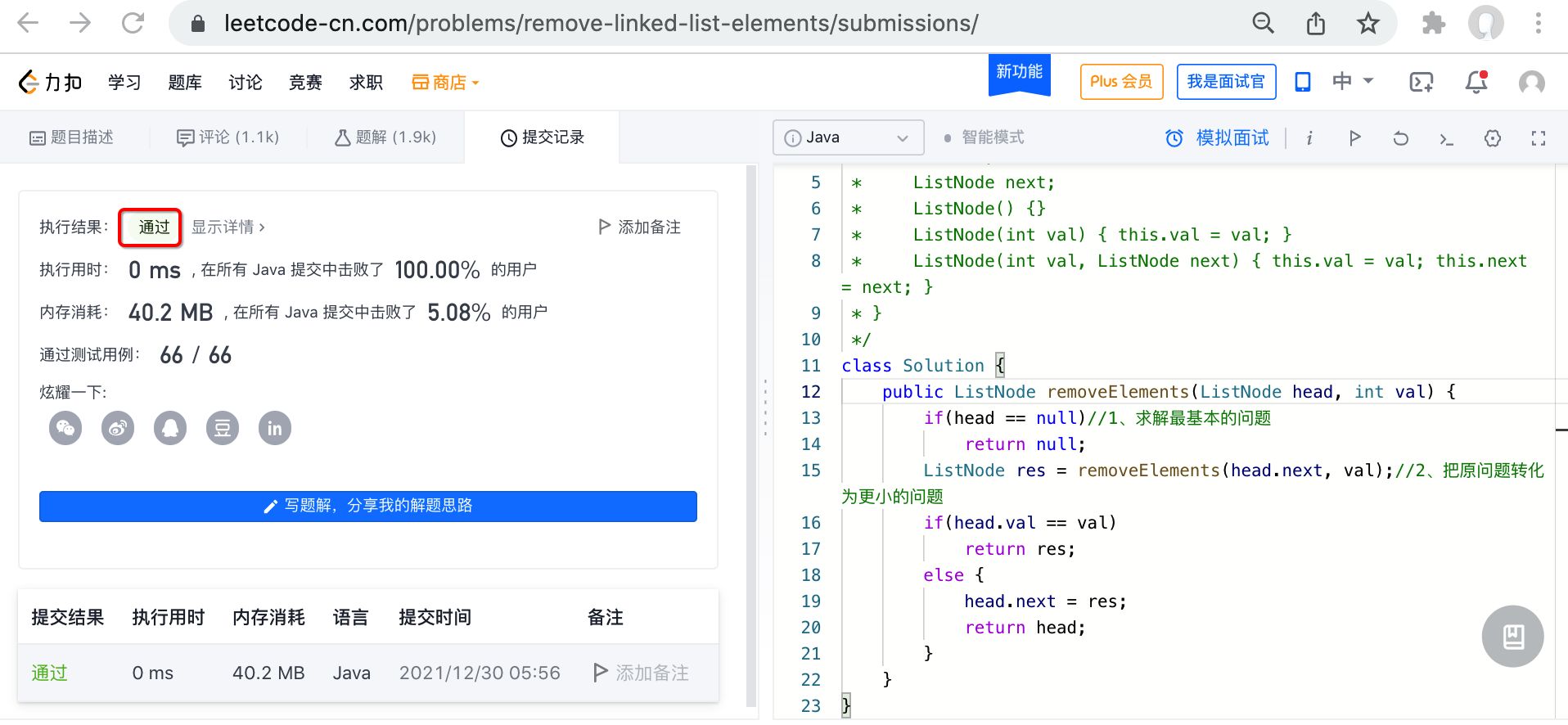
leetcode validation:
Next, copy our implementation to leetcode for verification:
Code optimization:
This logic can be simplified:
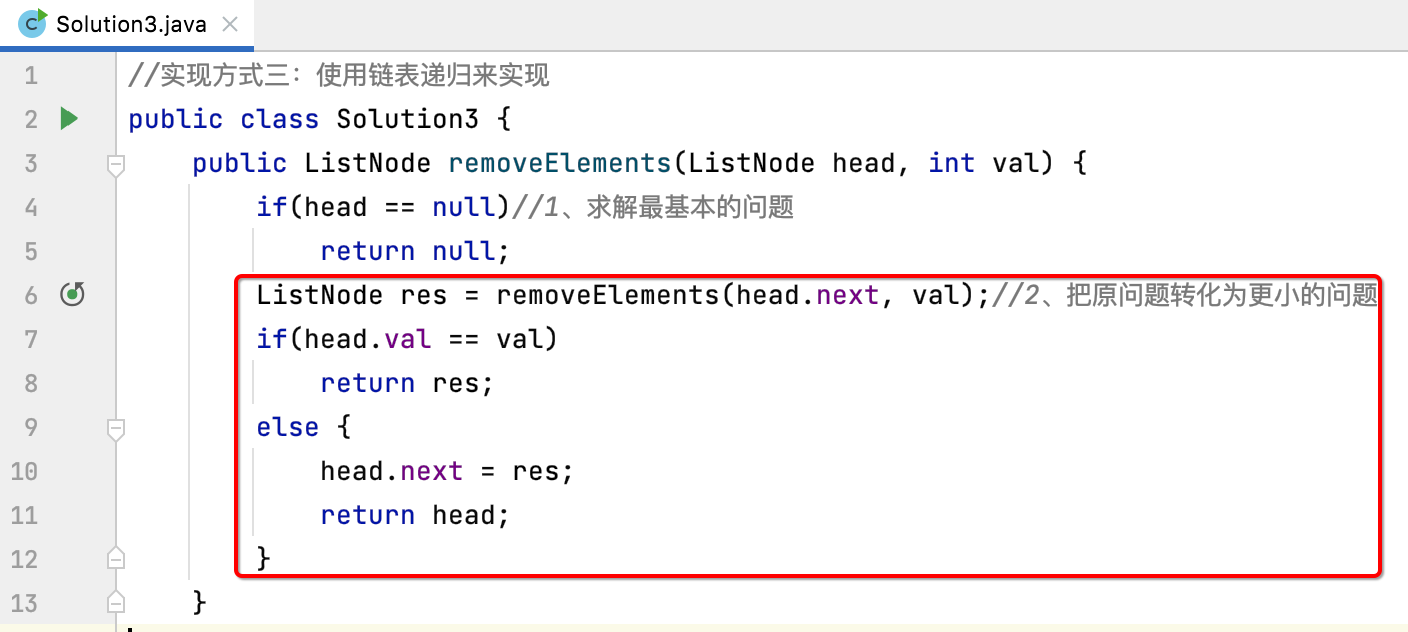
How to streamline it? As follows:
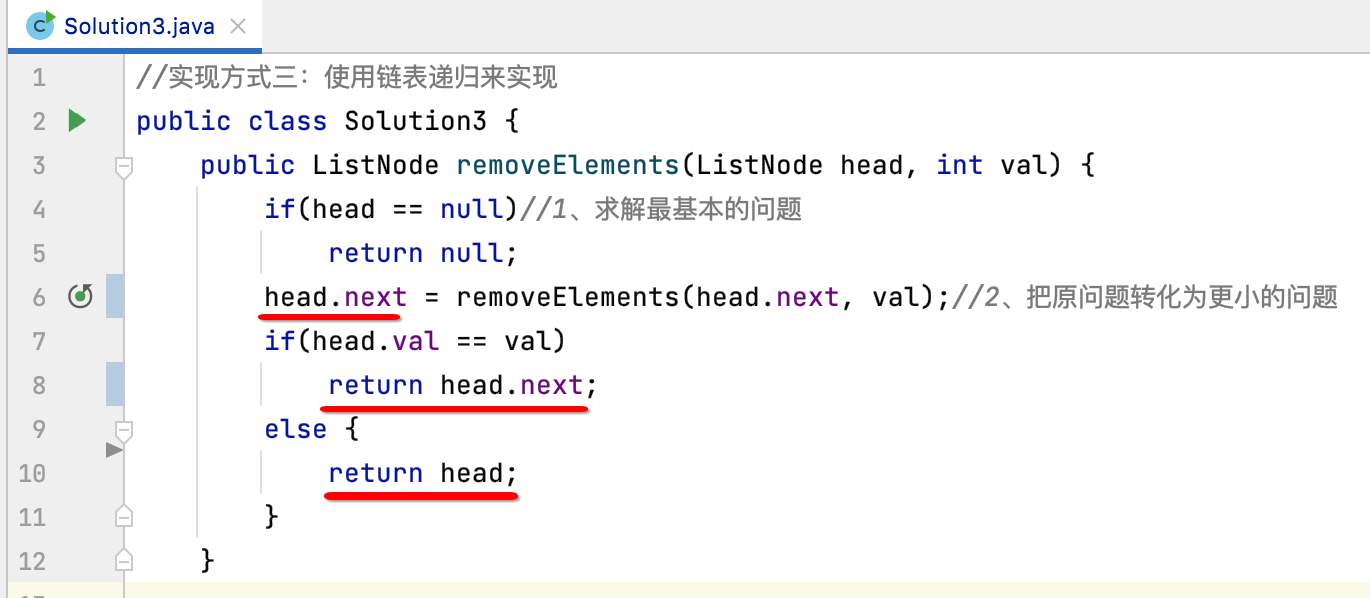
This condition can be reduced to a three item operation statement:
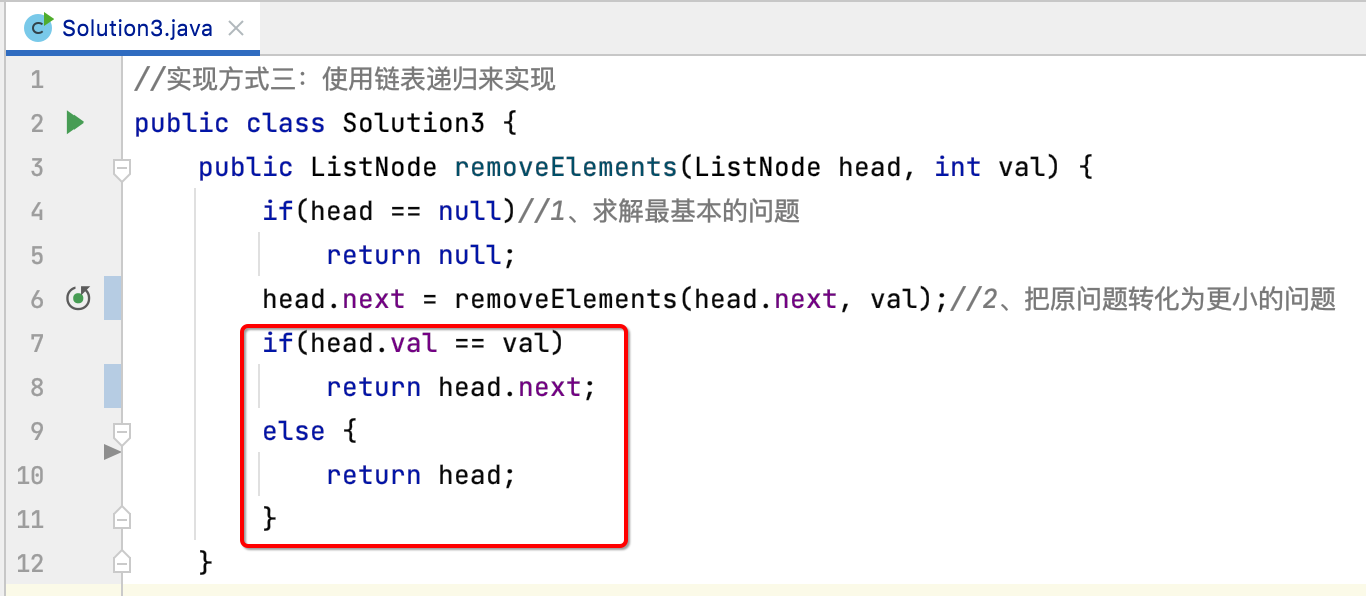
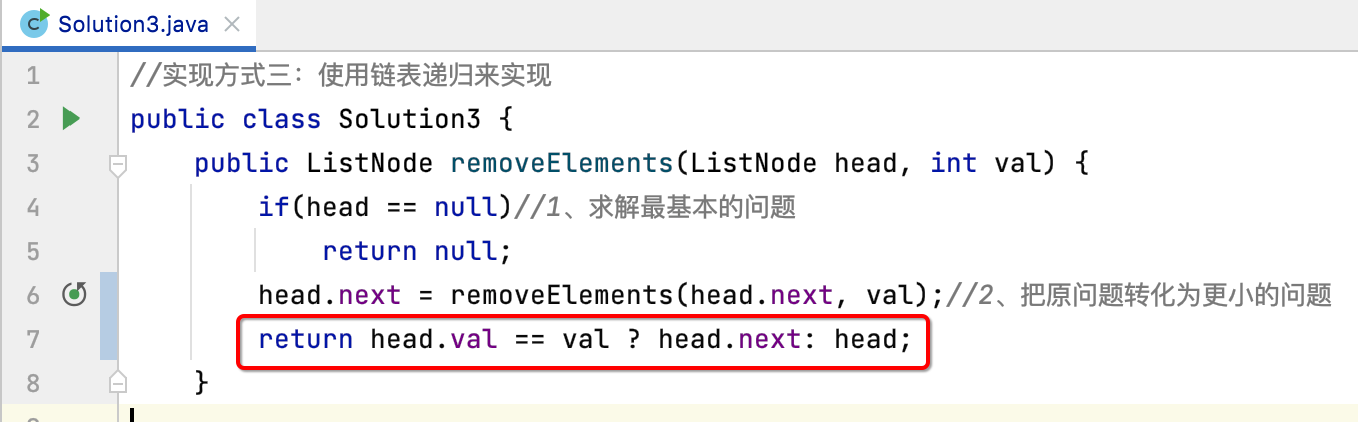
Also submit to leetcode for verification:
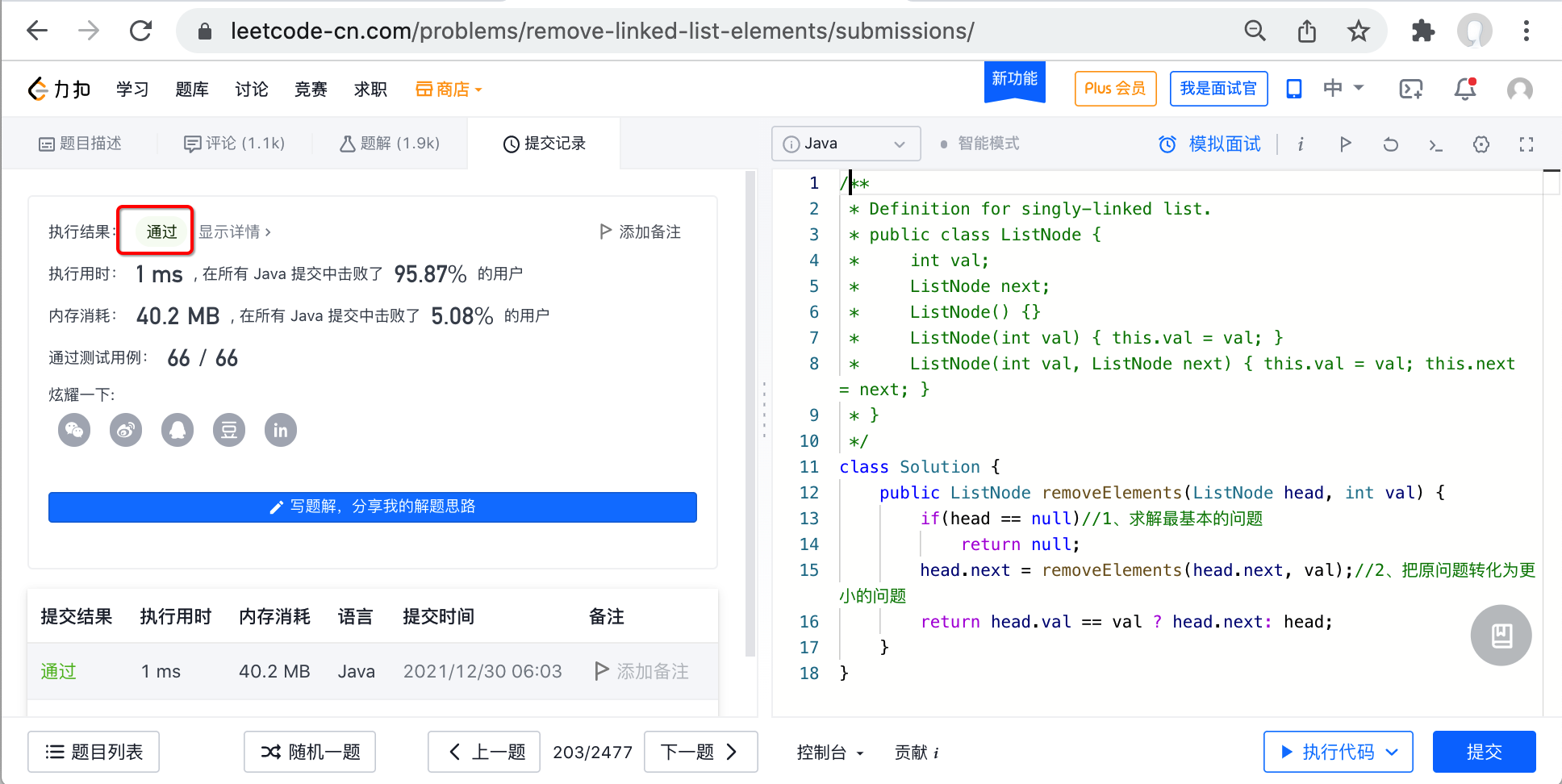
Is the code simpler than the previous non recursive method? You can compare:
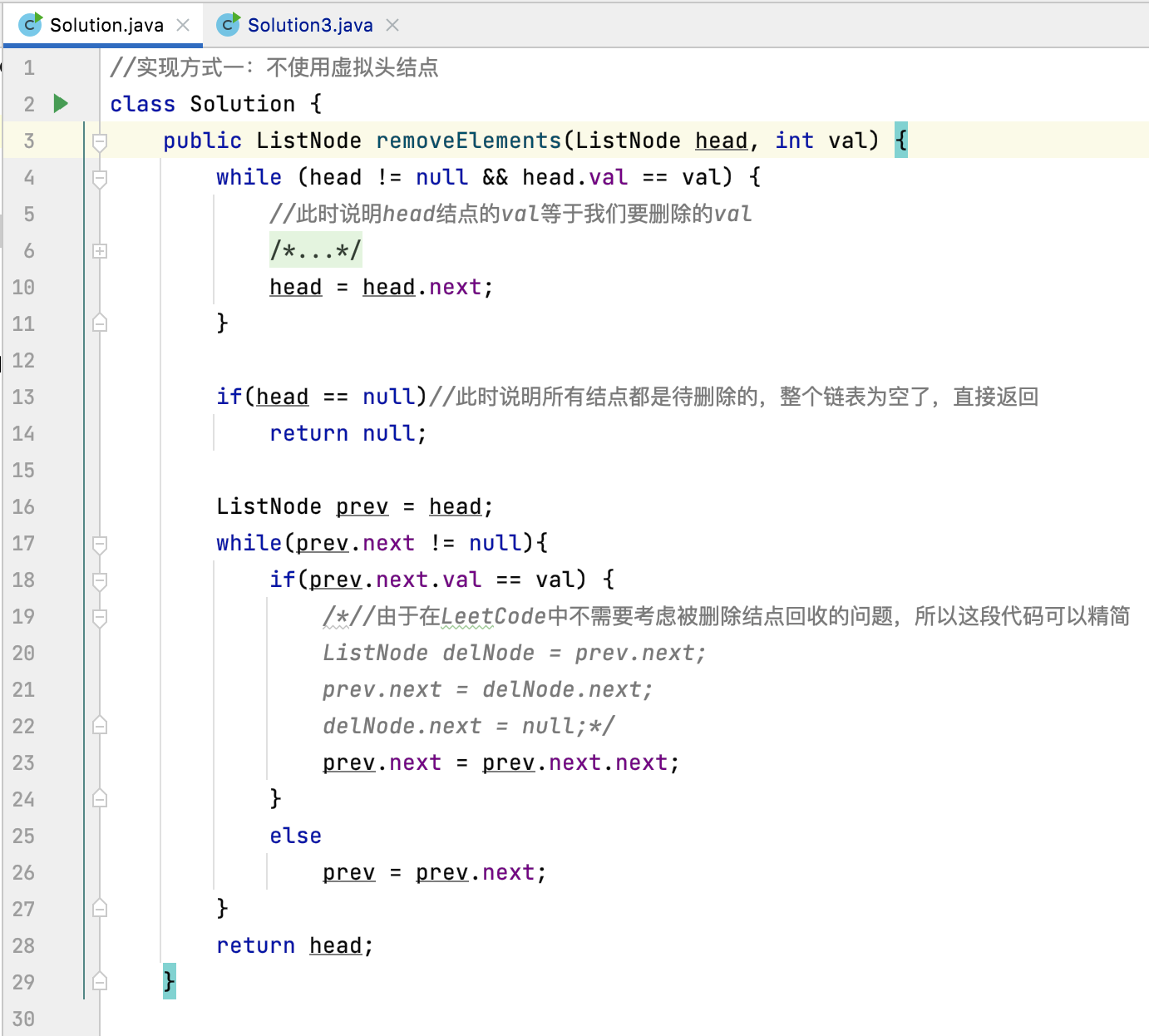
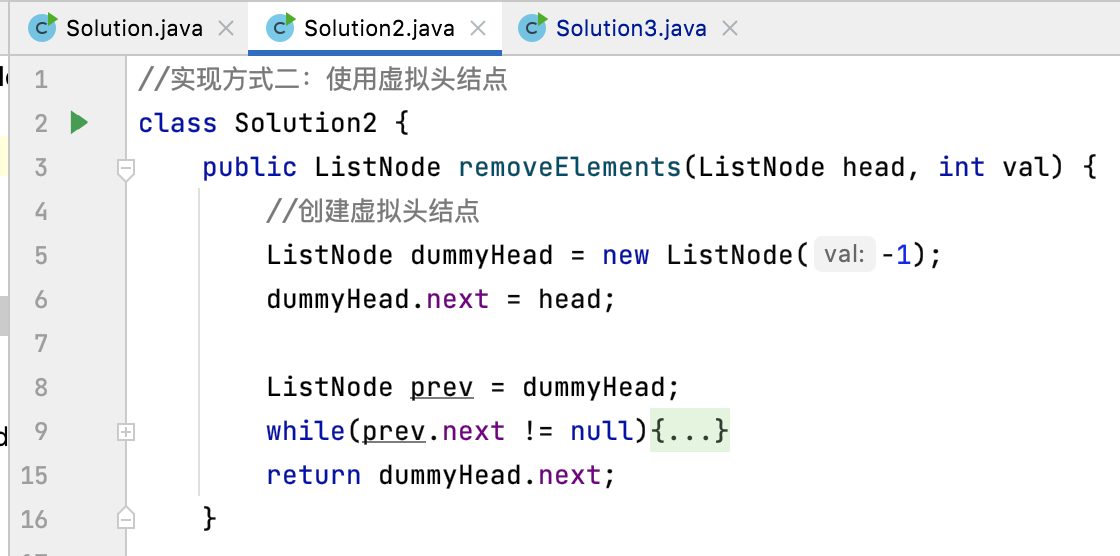
This is a normal evolution process [you can write recursively at first, but at least I can use non recursive methods]. Finally, you will find that the code implemented by recursion is relatively concise. In addition, when writing recursive logic, you input it from the macro semantics, If you have to struggle with the operation mechanism of recursion, it will be very painful. It's easy to faint around. This is an empirical way to write recursion.
Mechanism of recursive operation: Micro interpretation of recursion:
When inputting and writing recursion above, we always emphasize that we must input and write from a "macro" perspective, because it is easier to understand, but!!! Can the internal operation mechanism of recursion be completely ignored? Of course not, so next, analyze the internal operation mechanism of recursion from the perspective of "micro", so that you can understand recursion from both macro and micro perspectives.
Application of memory stack:
In essence, recursive logic is still a function call function, right? Program call is actually a system stack, which is actually before https://www.cnblogs.com/webor2006/p/14216904.html Already learned:

The process of the whole system stack is as follows:
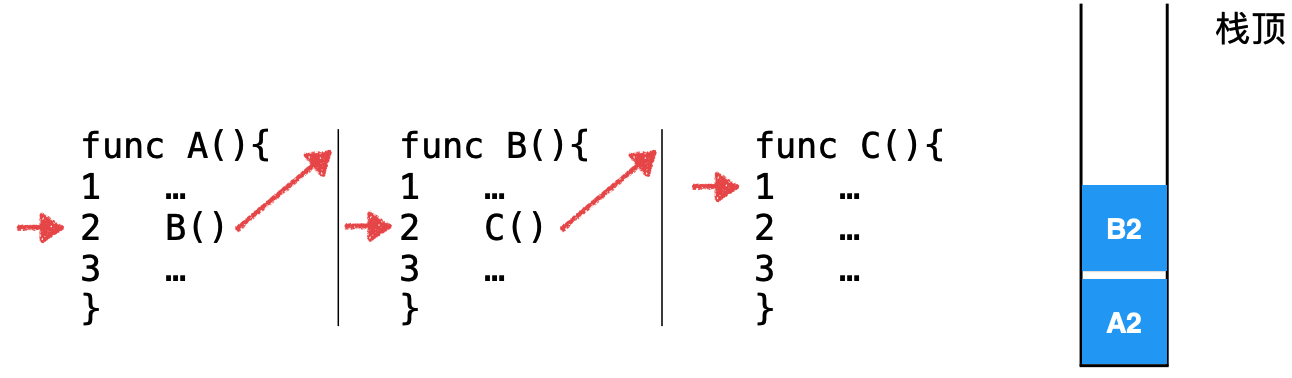
When the child function C is called, it will find the last position in the system stack where the parent function called the child function and continue to execute. The recursive call is different from it, but the function call itself.
Analysis 1: use recursion to solve the sum of array elements
We have implemented such a simple recursive program before:
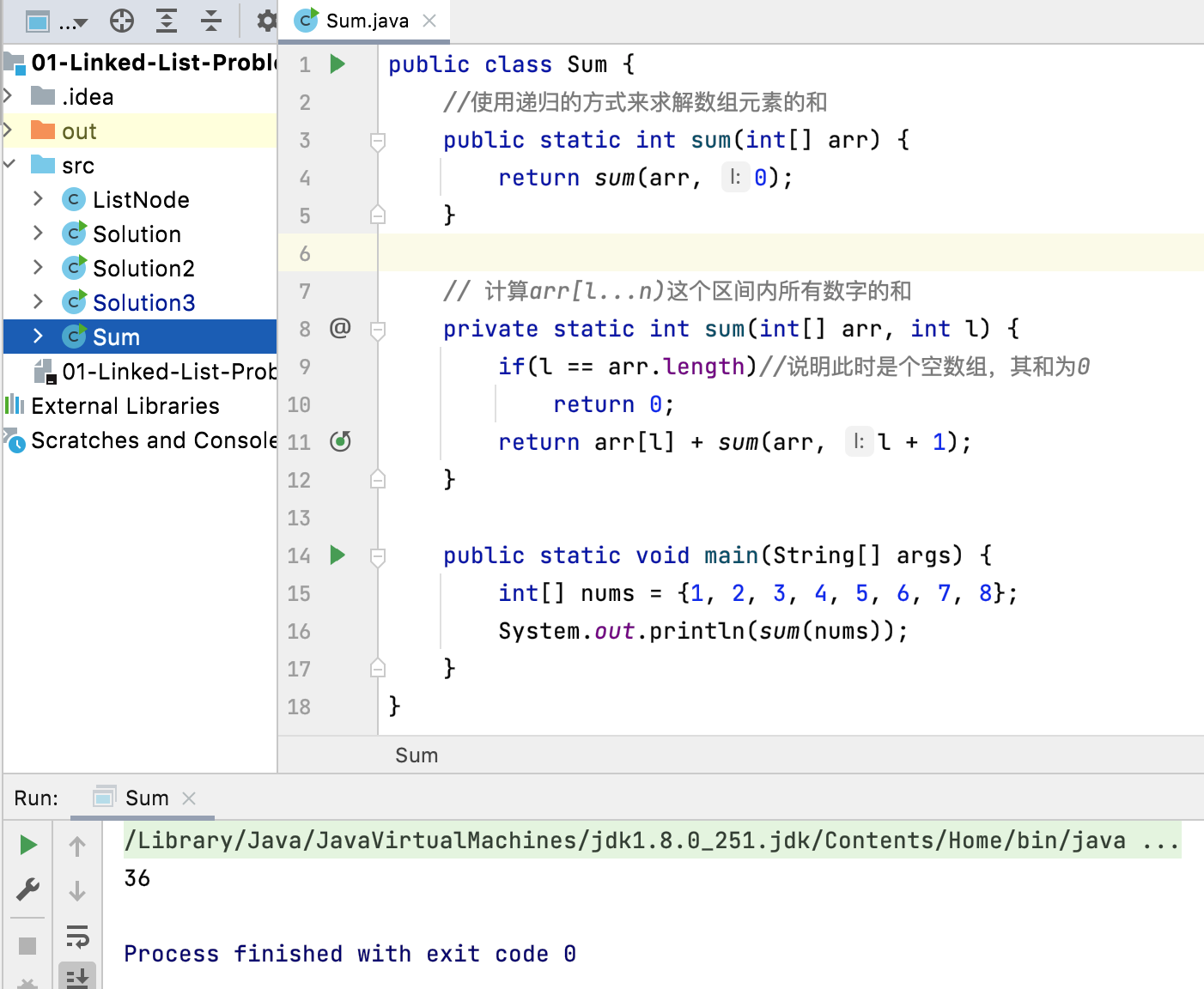
Next, let's analyze the whole internal operation process of the recursive program.
Adjustment Code:
In order to facilitate the analysis of the program, let's adjust the implementation of recursion:

That is to split the original one line into two lines:
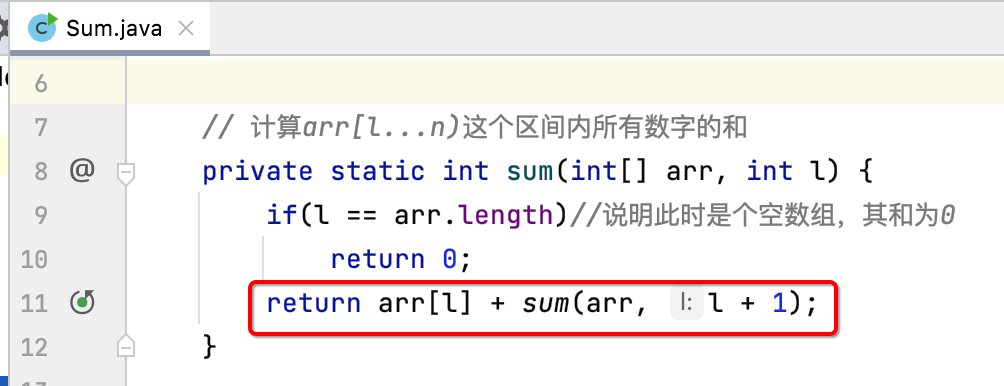
In addition, change the first condition:

Start analysis:
Here, take such a simple array as an example for analysis:
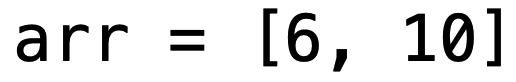
1. Call sum(arr, 0)
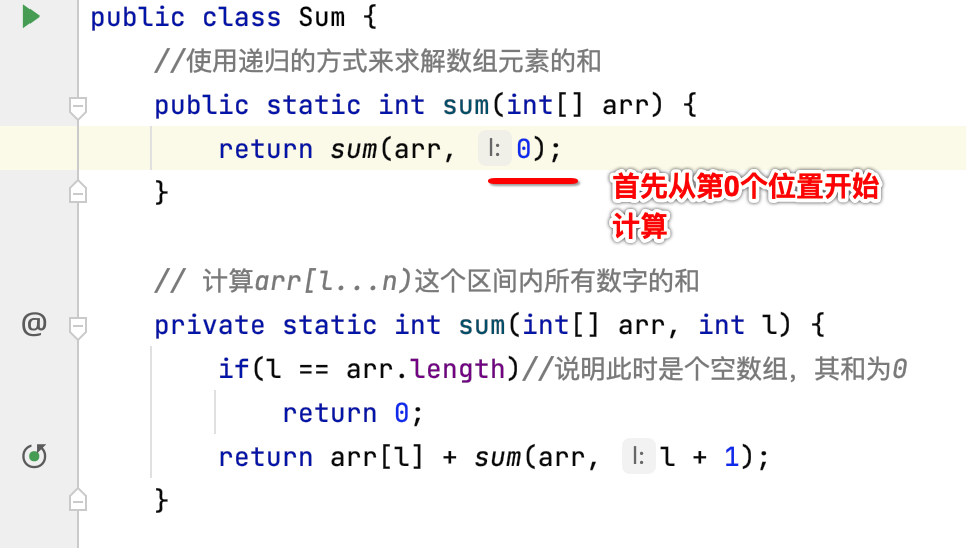
The first sentence will be executed:

Obviously, it doesn't work, right, so go ahead and execute it:

At this point, you enter a recursive call, right? For recursive calls, you actually call the following functions.
2. Call sum(arr, 1)

As like as two peas, the logic of the first function call is exactly the same, but for the sake of understanding, it is broken down and decomposed.

Obviously, the conditions are not met, right? Continue:

At this time, another recursive call occurs, which is the call process of a sub function.
3. Call sum(arr, 2)

At this time, the first condition has been established, so 0 is returned directly, so at this time:

4. sum(arr, 1) continues:

At this point, the function can return, so:

4. sum(arr, 0) continues:
Continue at this point:

Finally, the whole recursion ends, and the result is 16:

Summary:
So far, the whole internal operation mechanism of this simple recursive program has been sorted out, which actually reveals that when you are a little difficult to understand the operation mechanism of a recursive function, sorting in this way will be more clear and easy to understand.
Analysis 2: delete the elements in the linked list
The above recursive program may be too simple. Let's take this program as an example for micro level analysis:
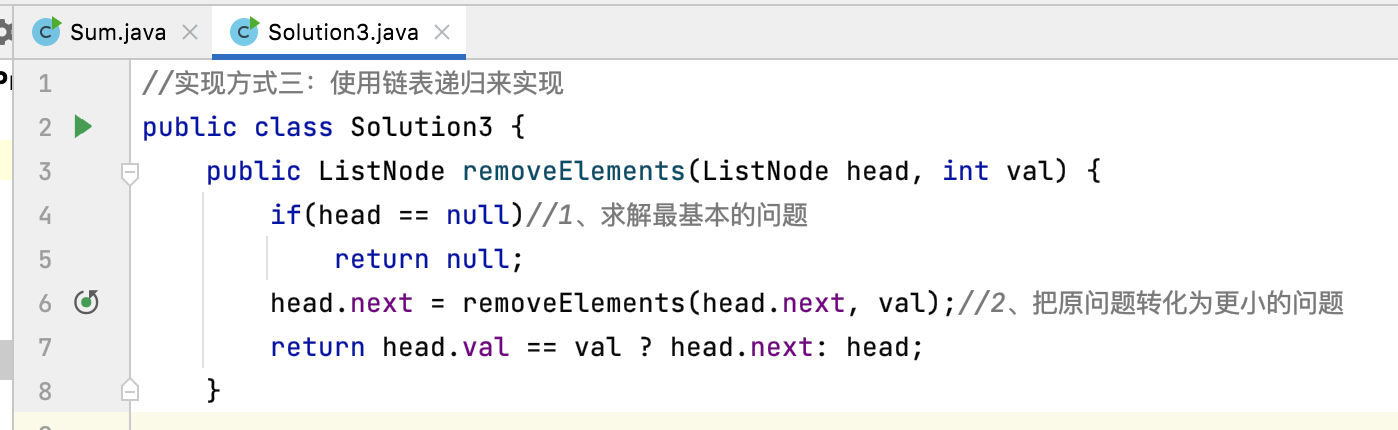
In order to facilitate analysis, first mark the code of the function inside with a serial number:

Similarly, a simple linked list data is used for simulation:
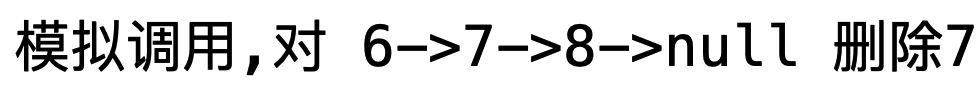
Start analysis:
1. First removeElements call:
The head linked list passed in at this time is:

Perform the first step:

Then execute the second step and start the recursive call:
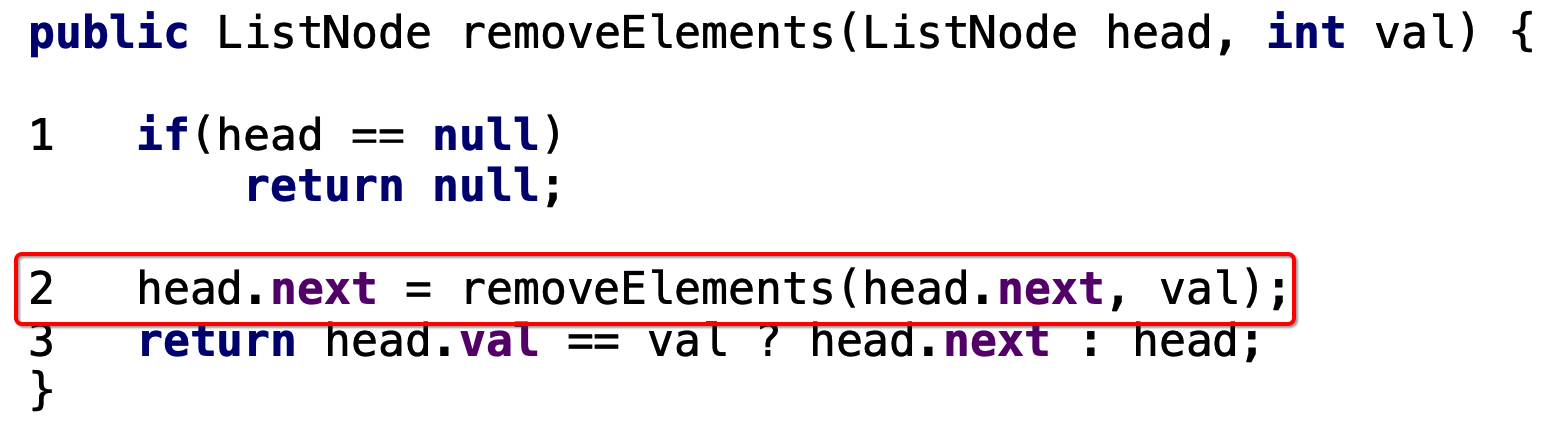
The status is:
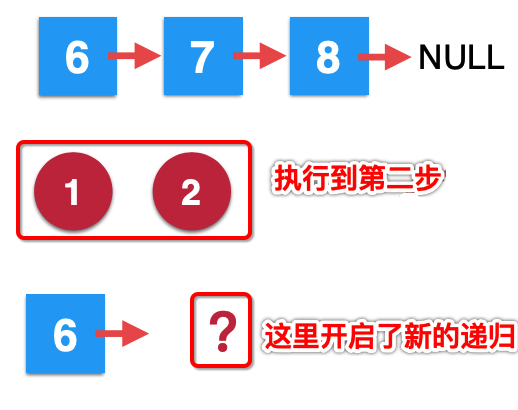
2. The second removeElements call:
Next, look at the second recursive call:
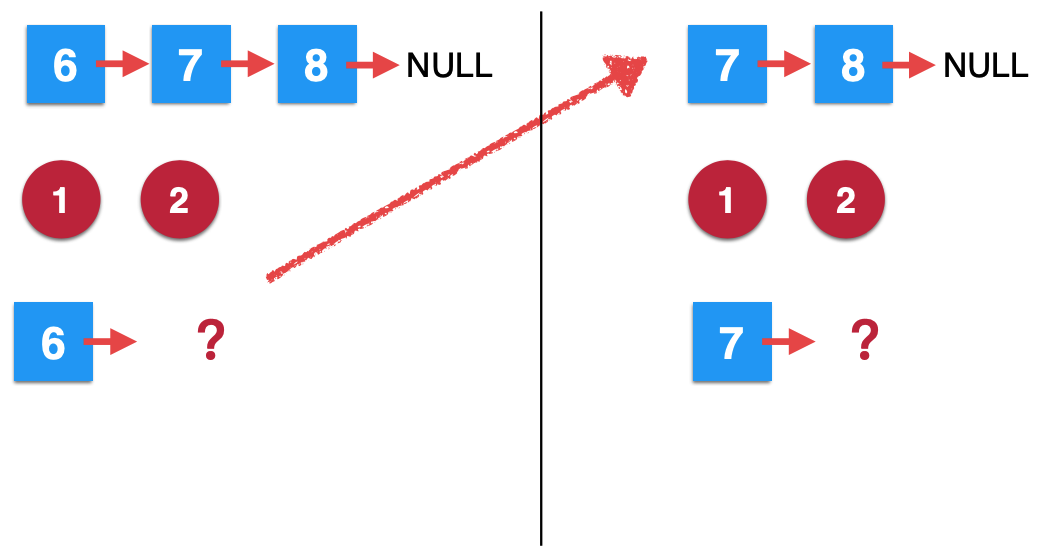
At this time, it also stops in the second step, and a new recursion is started again.
3. The third removeElements call:
Similarly, look at the third recursion:
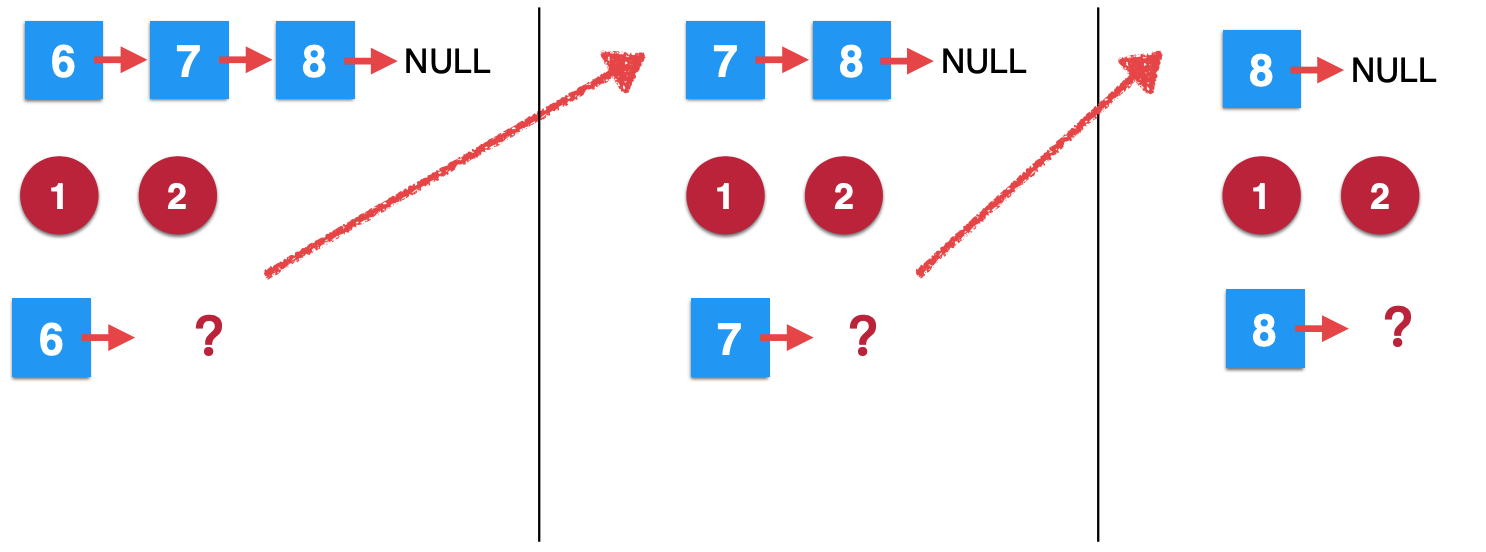
At this time, it also stops in the second step, and a new recursion is started again.
4. The fourth removeElements call:
Similarly, look at the fourth recursion:
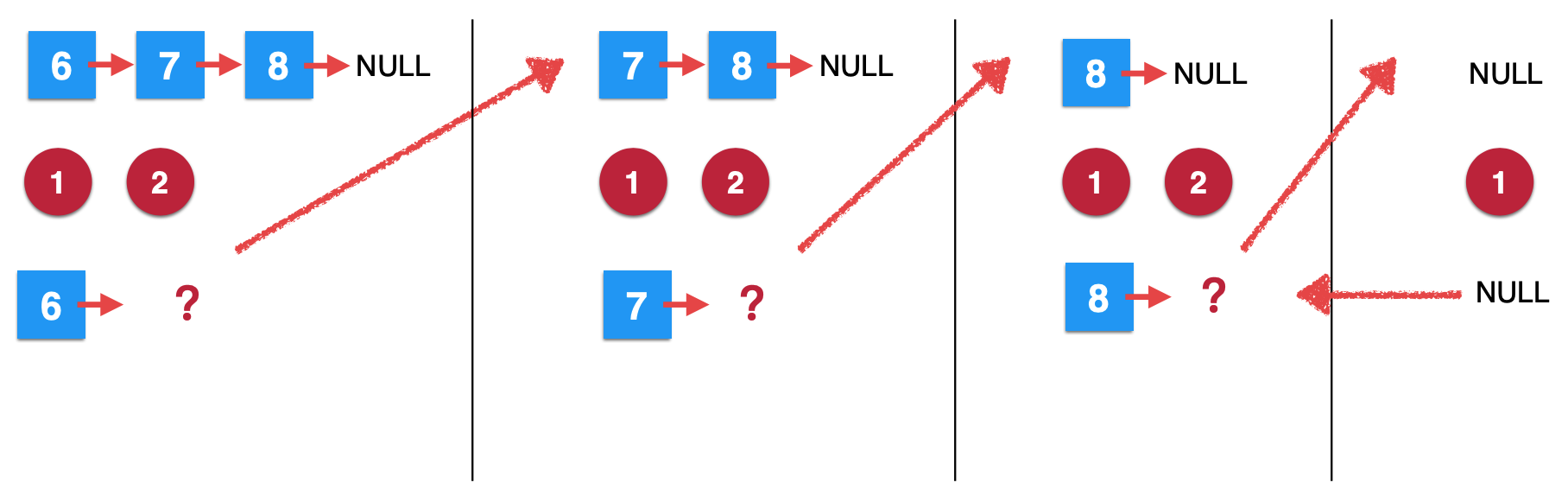
It is found that the conditions are met when the first sentence is executed, so the function call returns to the end.
5. The third removeElements call continues:
At this time, the result of this call will be displayed:

Next, you can continue to step 3. After execution, it is actually:
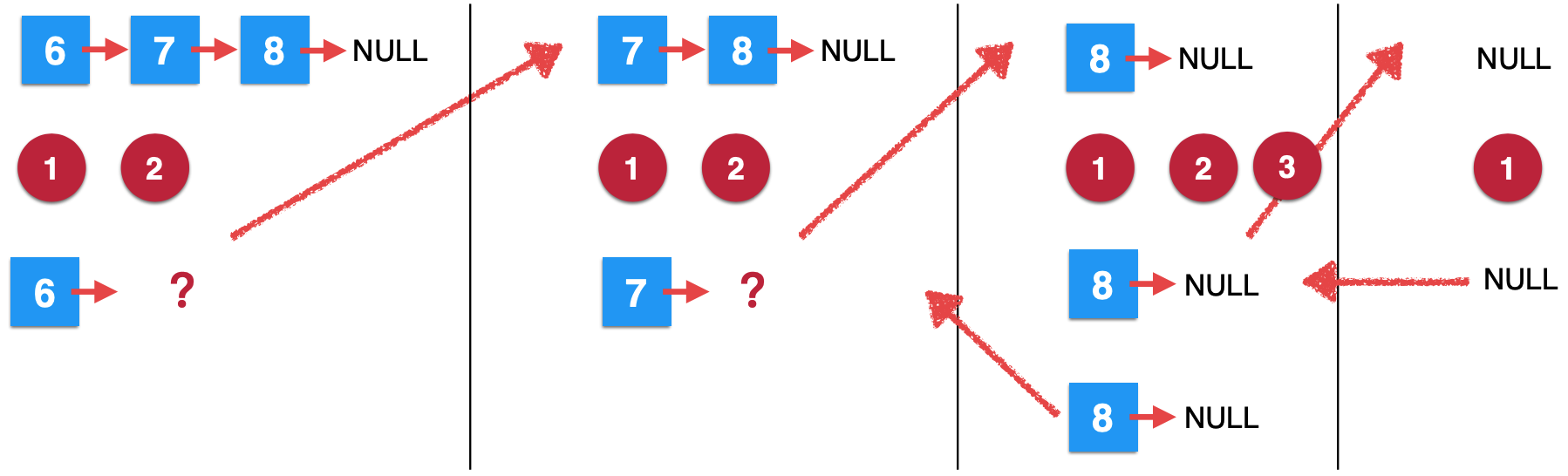
6. The second removeElements call continues:
At this time, the second recursive result comes out:
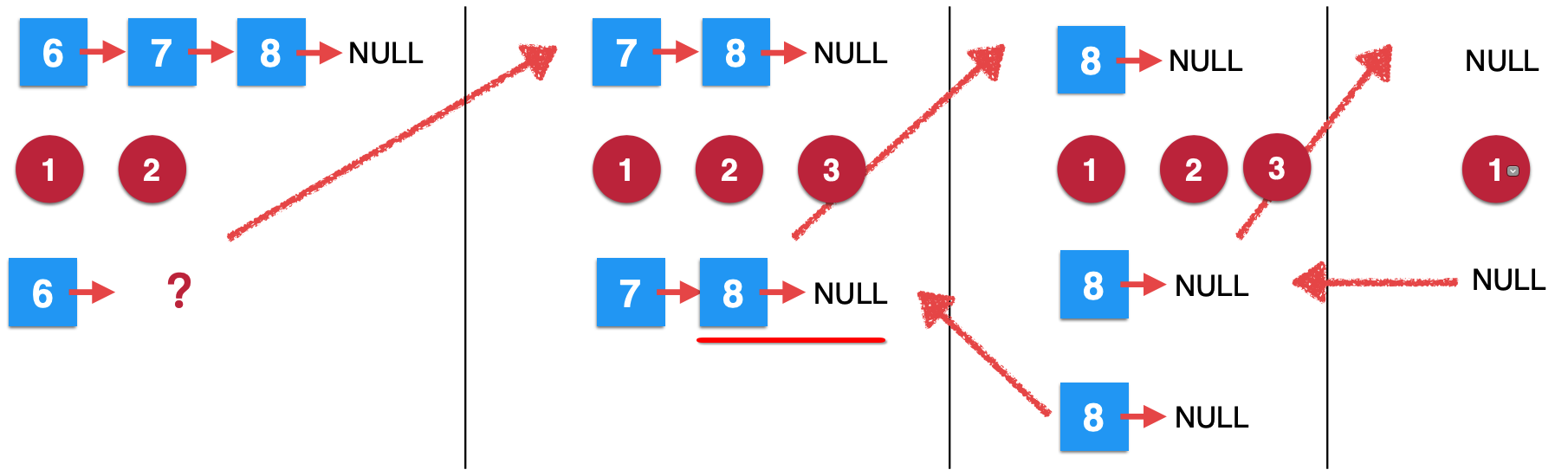
Then continue to step 3. Obviously, since the head at this time is just equal to the element 7 to be deleted, its next is returned, so it is as follows:
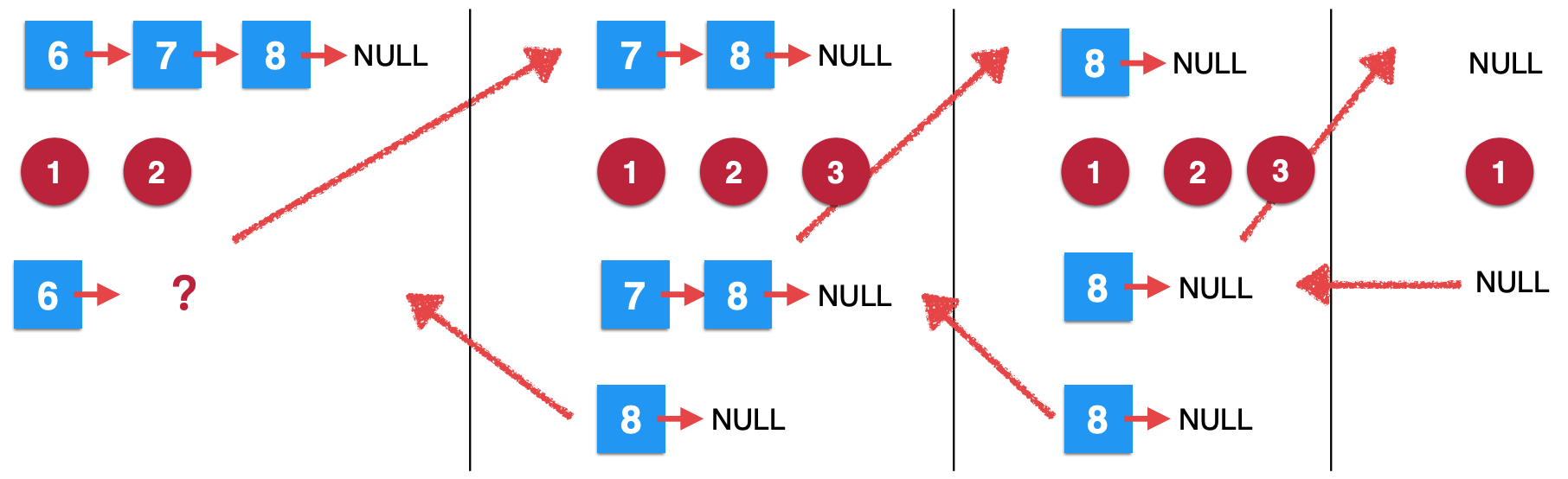
7. The first removeElements call continues:
With the same logic, the first call can continue to be executed, and finally the whole recursive algorithm can end, as follows:
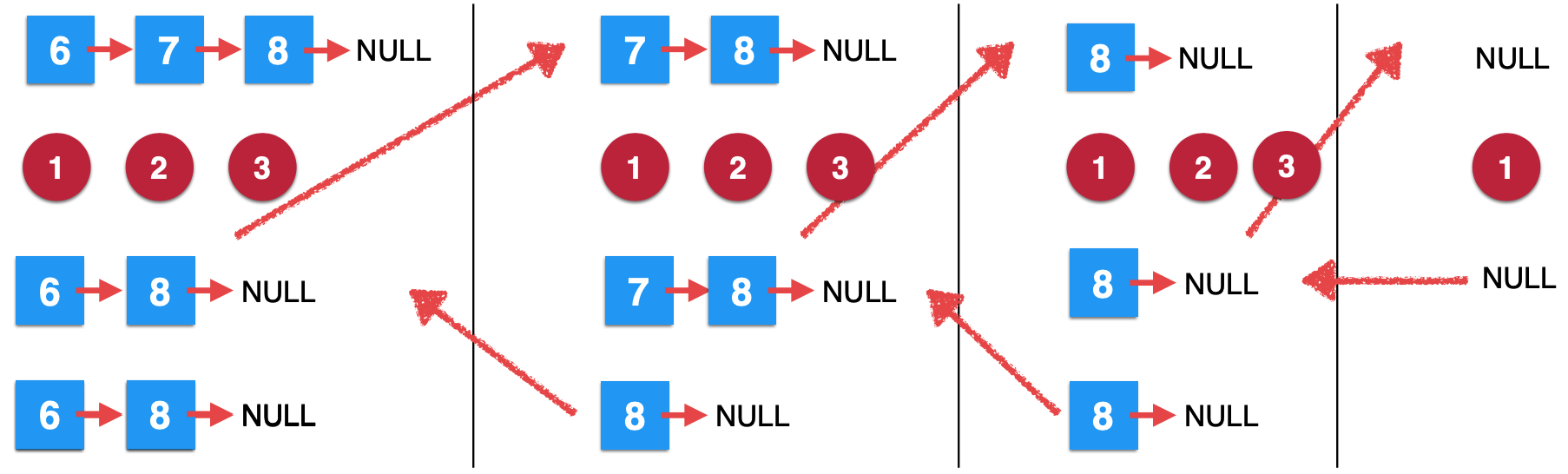
The final result is 6 - > 8 - > null.
Cost of recursive call:
Of course, we all know that recursive calls have system performance problems, mainly in the following aspects:
1. Function calls have time overhead, such as where the current function logic is executed, and so on.
2. The recursive call process will consume the system stack space. The most typical exception is StackOverFlow, right.
Since these costs exist, what is the value of recursion? In fact, the logic implementation of nonlinear data structure [tree and graph] will be simpler. In fact, it is not very obvious in linear structure. In addition, recursion is also clear in logic input and writing.
Debugging of recursive algorithm:
In the above, we understand our recursive program through the disassembly of recursive functions step by step, right? But the cost of sorting is a little high. In fact, there is another way to see the internal mechanism of the whole recursion, that is, log printing. By adding a certain log output to our recursive program, the whole recursive process is finally presented, Let's take the linked list deletion program as an example:
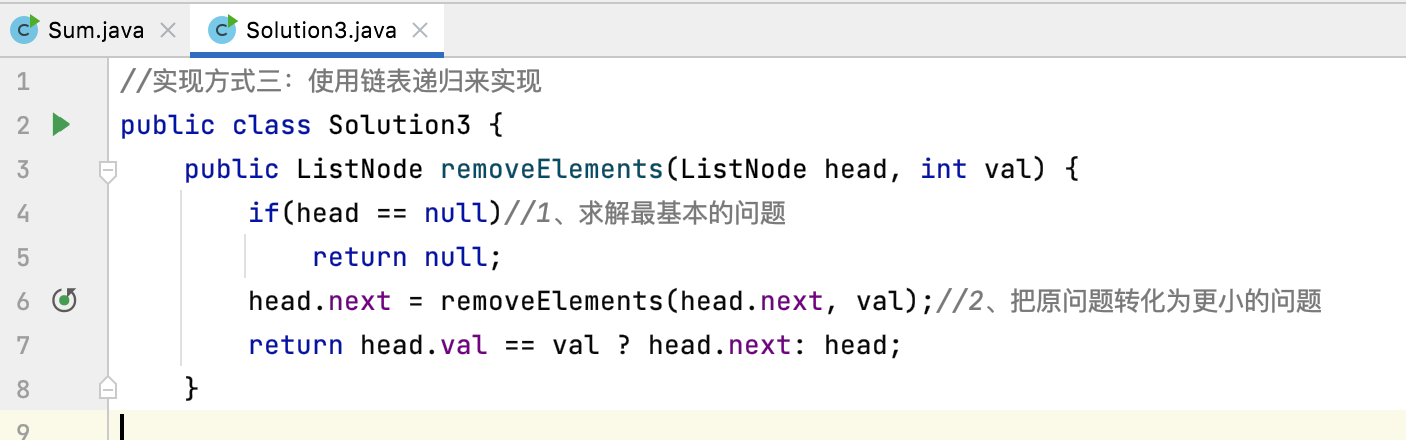
Let's revise it.
Add log:
In recursive calls, there is obviously a problem of trying. Therefore, in order to be more readable in the log output, a depth parameter is added here:
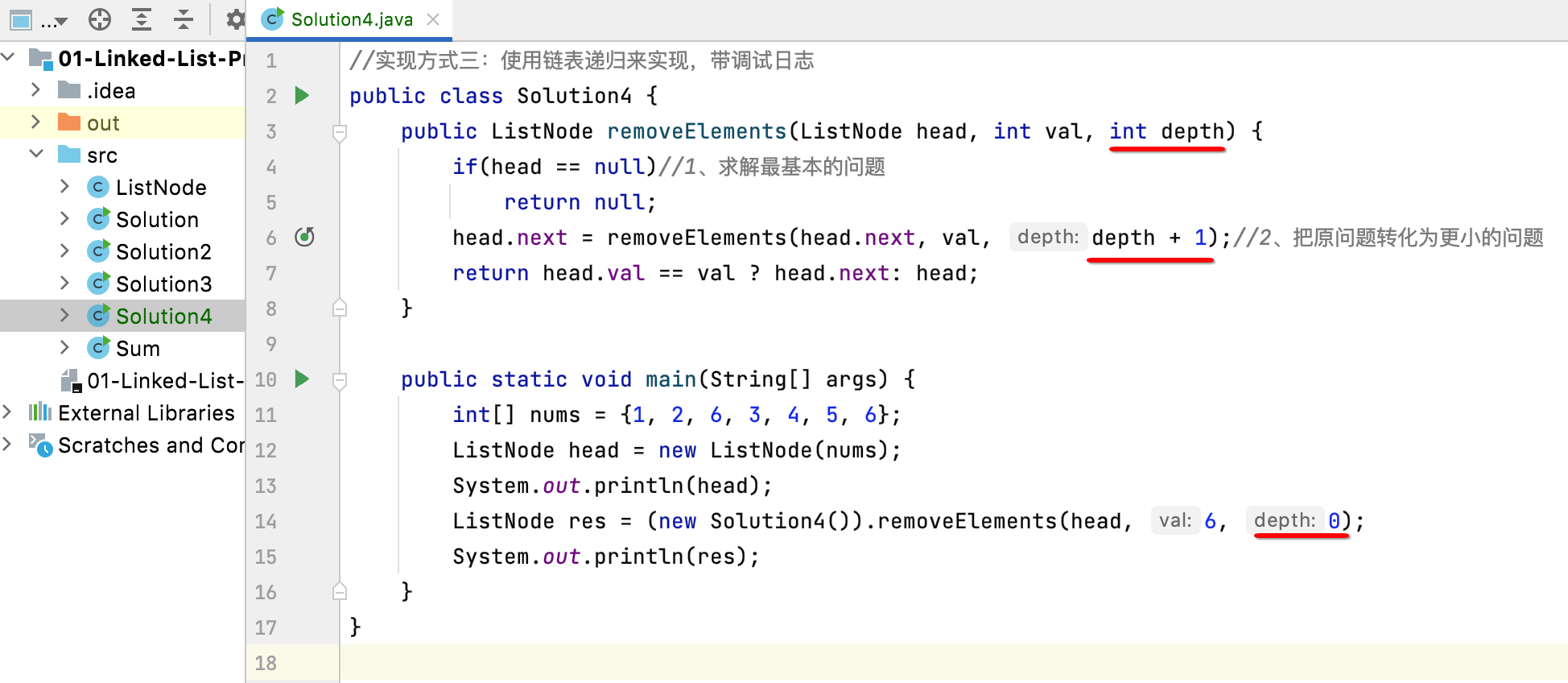
So you can print the calling depth first:
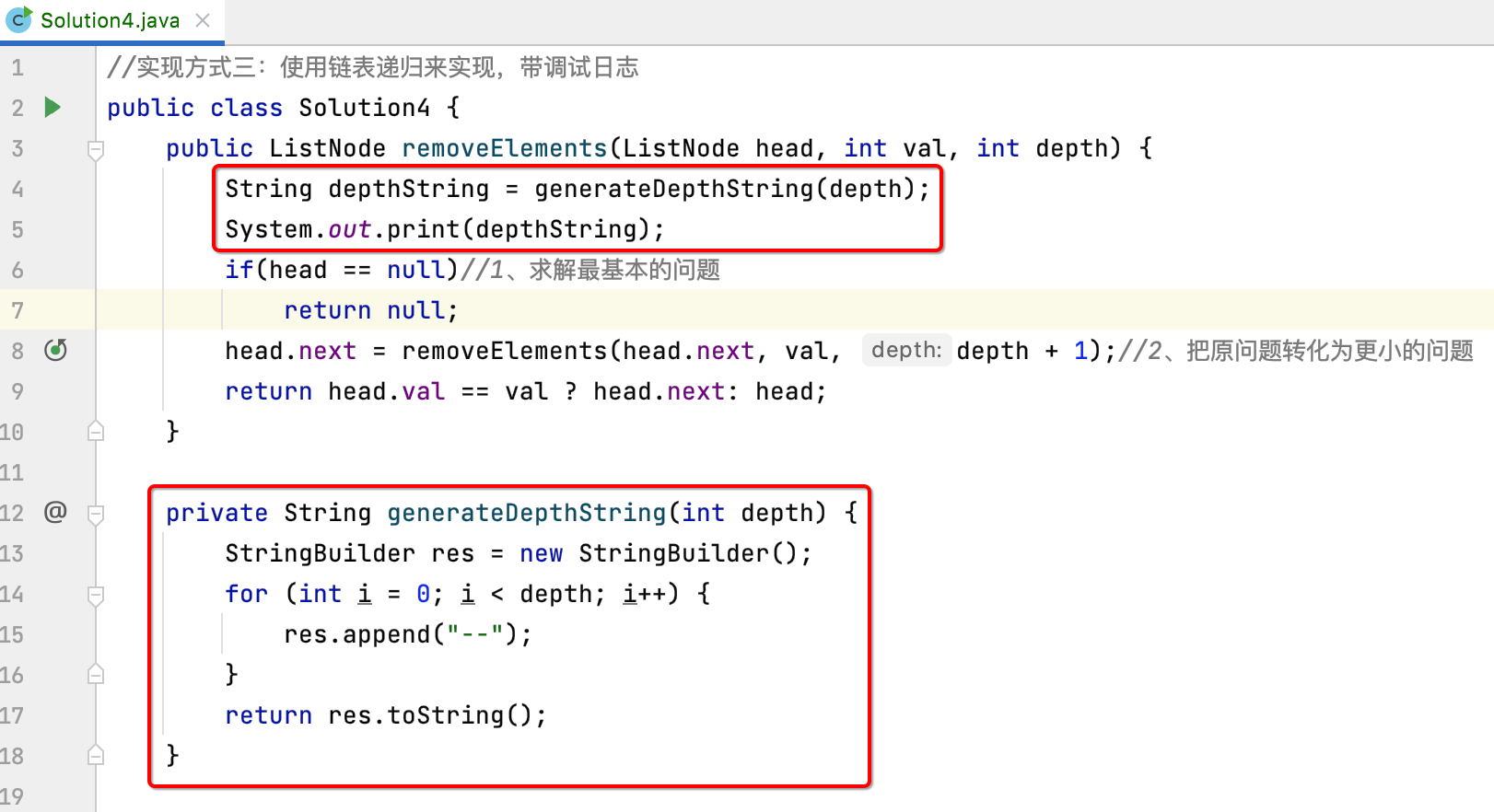
Then output the following sentence:
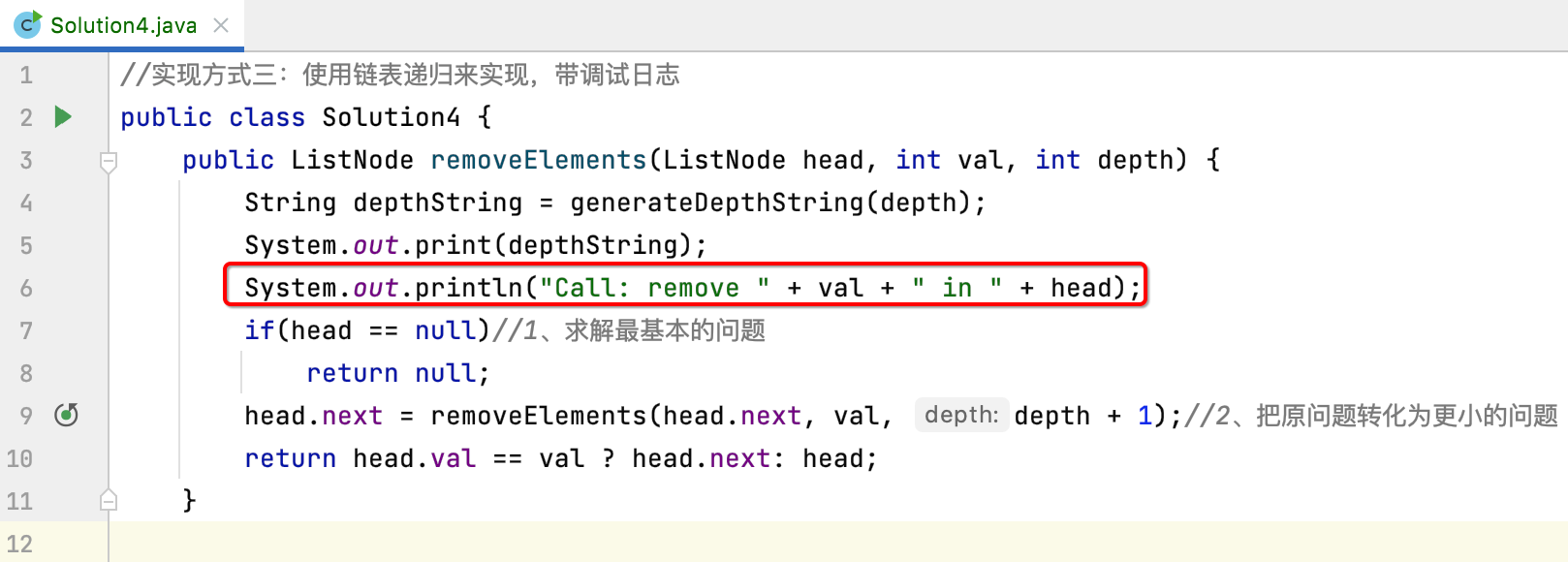
Then add some print to this condition:
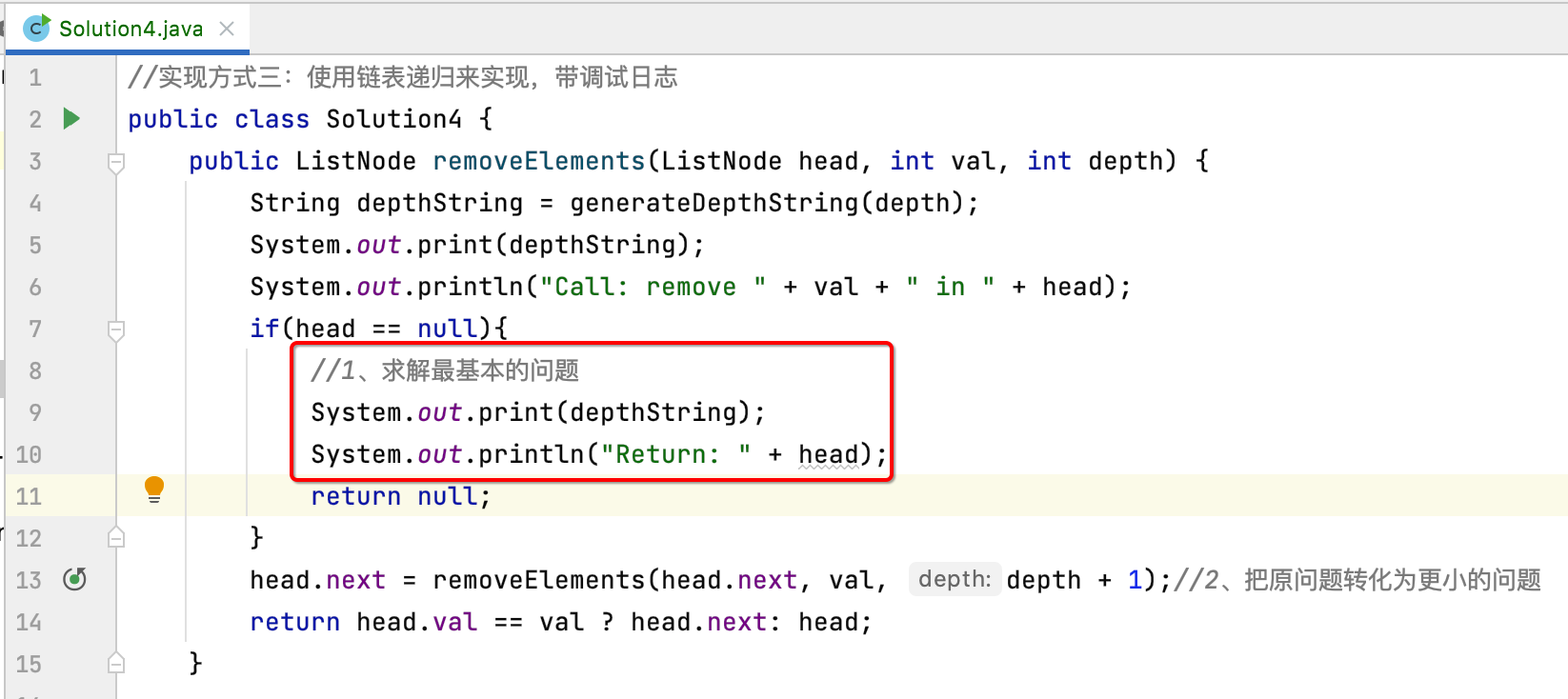
Next, you need to add logs to this Code:
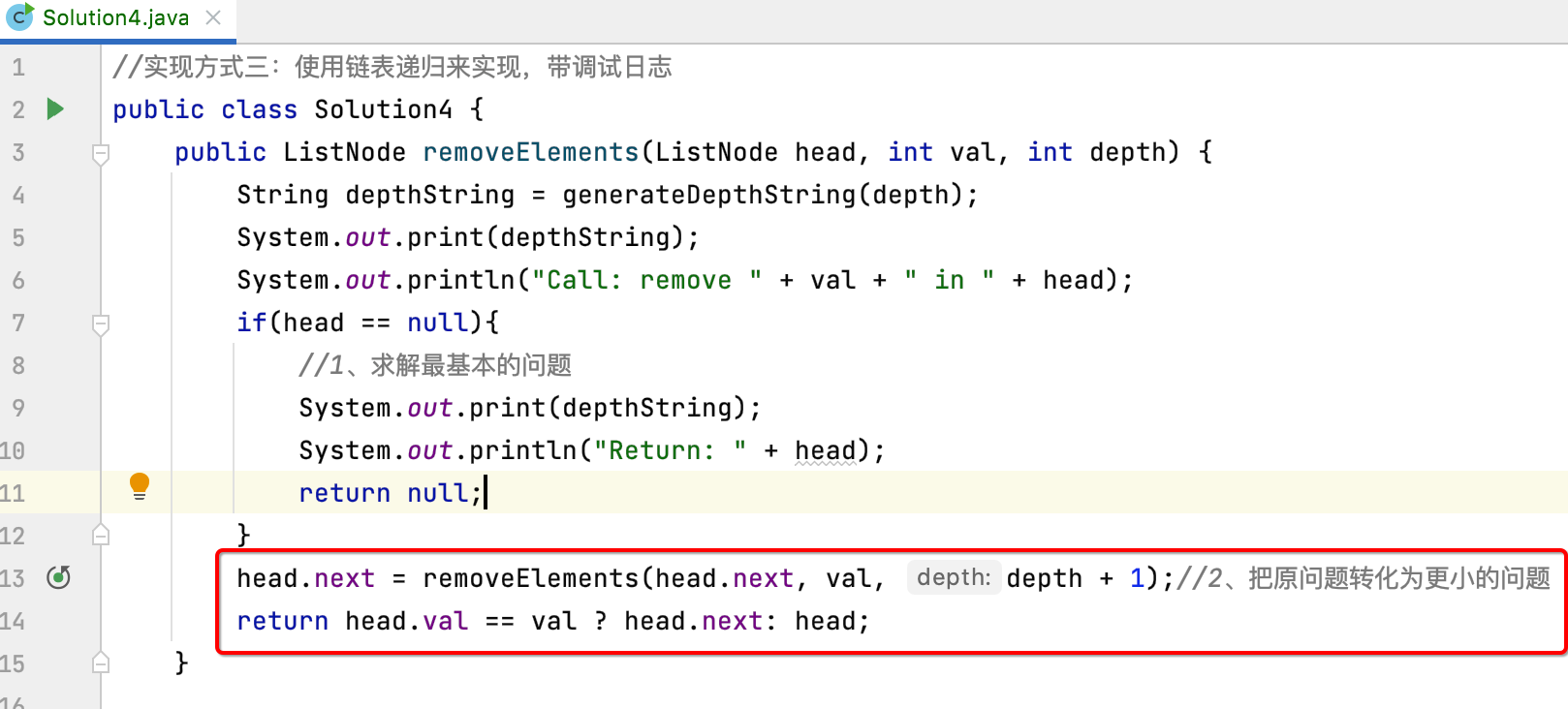
In order to print, it needs to be modified:
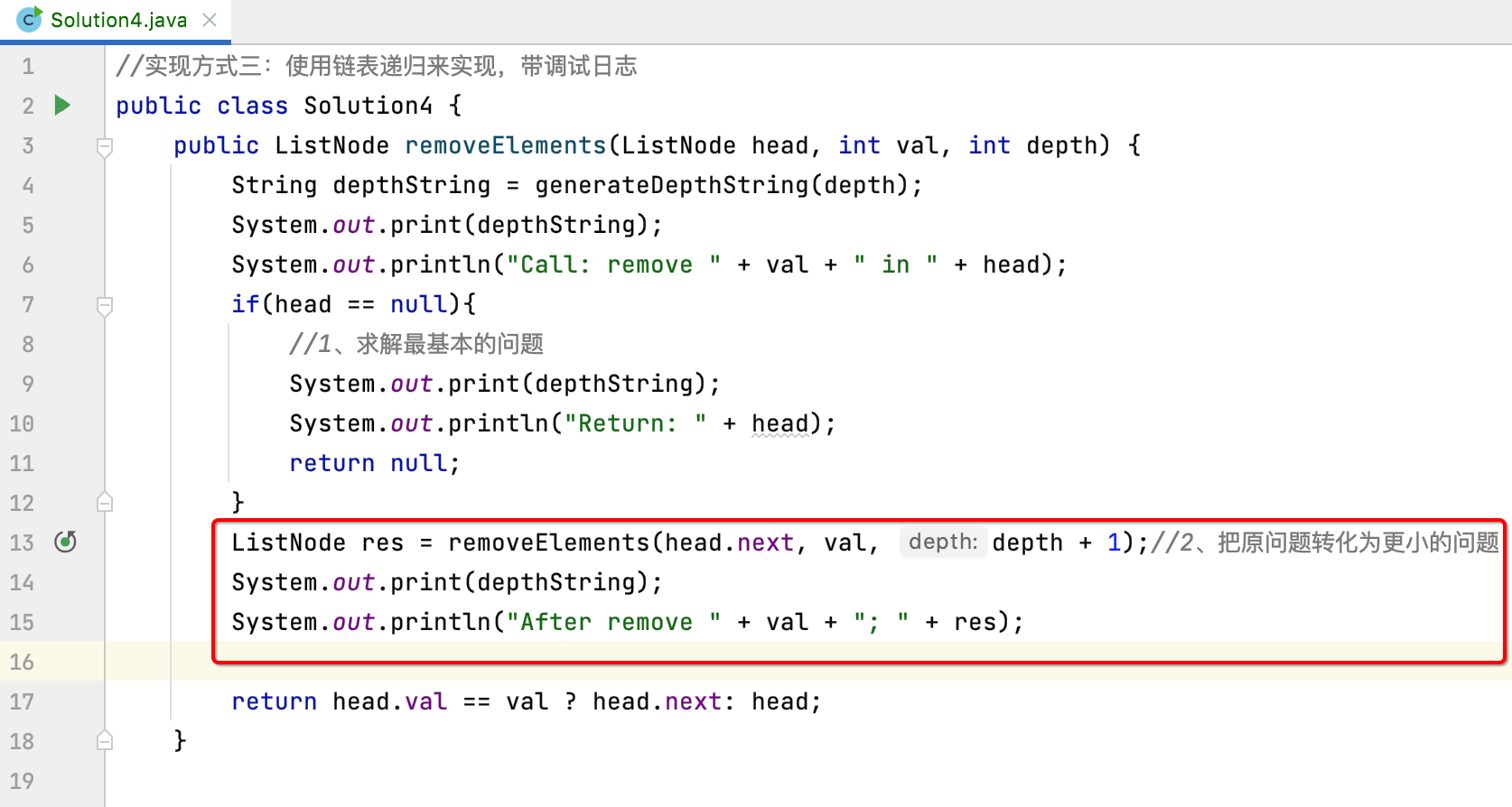
The final result return is also modified:
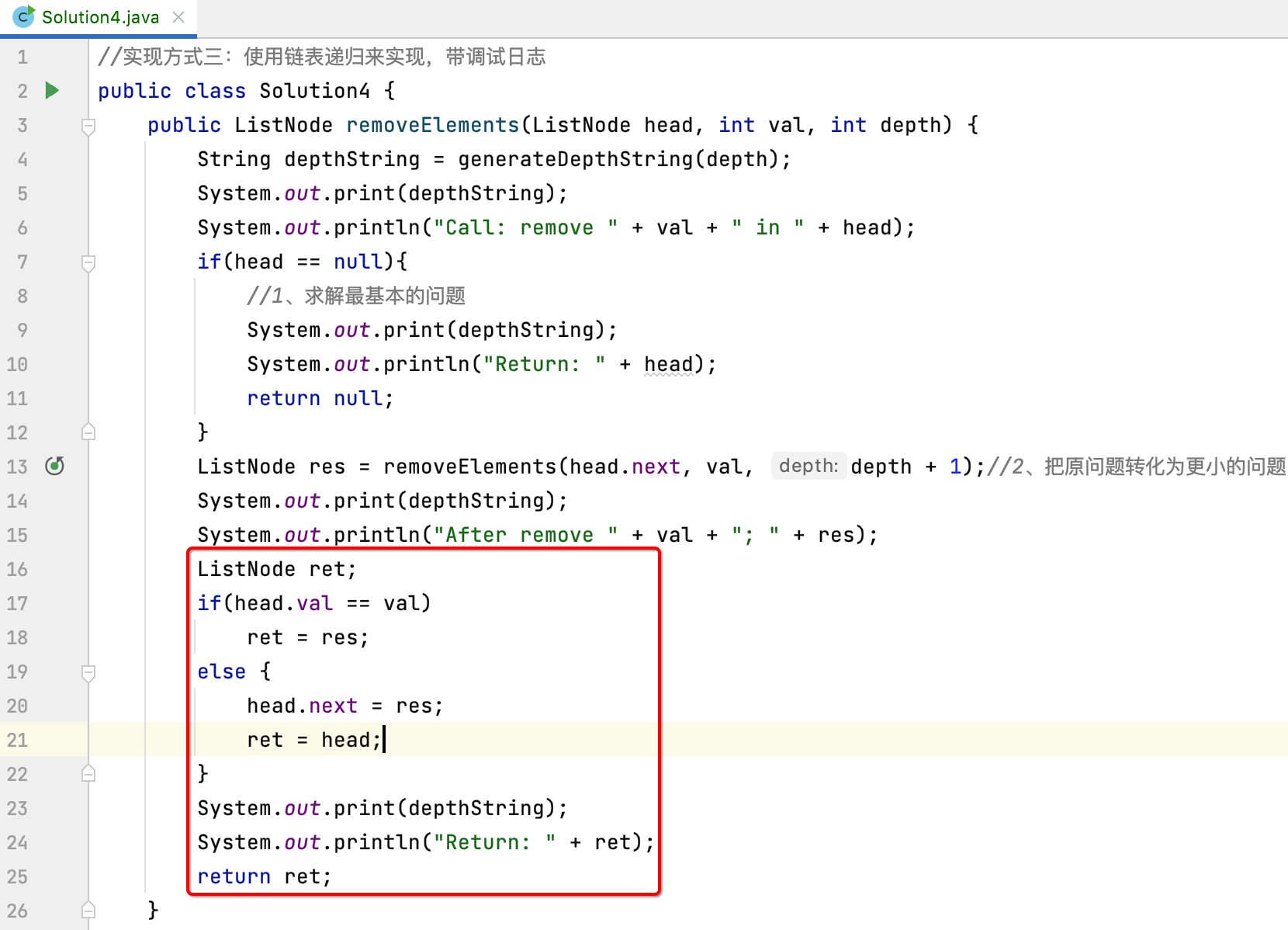
function:
Next, run to see:
/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/bin/java -Dfile.encoding=UTF-8 -classpath /Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/charsets.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/deploy.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/cldrdata.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/dnsns.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/jaccess.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/jfxrt.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/localedata.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/nashorn.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/sunec.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/sunjce_provider.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/sunpkcs11.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/zipfs.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/javaws.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/jce.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/jfr.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/jfxswt.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/jsse.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/management-agent.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/plugin.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/resources.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/rt.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/ant-javafx.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/dt.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/javafx-mx.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/jconsole.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/packager.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/sa-jdi.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/tools.jar:/Users/xiongwei/Documents/workspace/IntelliJSpace/algorithm_system_sudy/08-Recursion/01-Linked-List-Problems-in-Leetcode/out/production/01-Linked-List-Problems-in-Leetcode Solution4 1->2->6->3->4->5->6->NULL Call: remove 6 in 1->2->6->3->4->5->6->NULL --Call: remove 6 in 2->6->3->4->5->6->NULL ----Call: remove 6 in 6->3->4->5->6->NULL ------Call: remove 6 in 3->4->5->6->NULL --------Call: remove 6 in 4->5->6->NULL ----------Call: remove 6 in 5->6->NULL ------------Call: remove 6 in 6->NULL --------------Call: remove 6 in null --------------Return: null ------------After remove 6; null ------------Return: null ----------After remove 6; null ----------Return: 5->NULL --------After remove 6; 5->NULL --------Return: 4->5->NULL ------After remove 6; 4->5->NULL ------Return: 3->4->5->NULL ----After remove 6; 3->4->5->NULL ----Return: 3->4->5->NULL --After remove 6; 3->4->5->NULL --Return: 2->3->4->5->NULL After remove 6; 2->3->4->5->NULL Return: 1->2->3->4->5->NULL 1->2->3->4->5->NULL Process finished with exit code 0
It's still a little dizzy. Yes, but this output helps us see the whole recursive process, which still plays a great role in the analysis program.
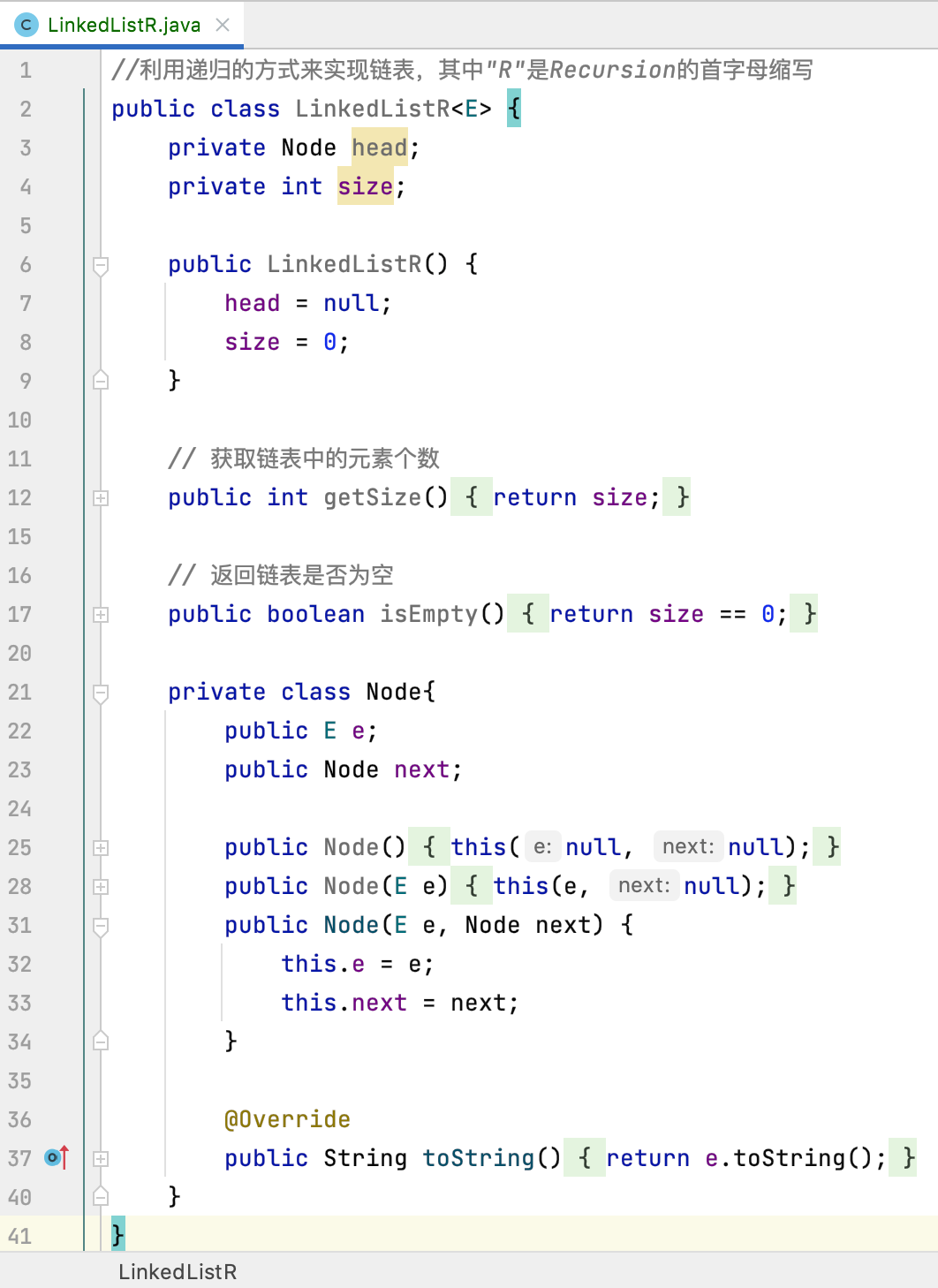
Recursive implementation of linked list:
Since the linked list has natural recursion, let's talk about it before https://www.cnblogs.com/webor2006/p/15319904.html Can all the linked lists be implemented in a recursive way? The answer is yes. The addition, deletion, modification and query of the linked list can be realized by recursion. Although it may not be done in practice, it is beneficial to do such an exercise in order to strengthen the understanding of recursion.
Let's recall that there are two ways to implement the linked list. One is without virtual head node, and the other is with virtual corresponding node:
//Version with virtual head node public class LinkedList<E> { private Node dummyHead;//Virtual head node private int size; public LinkedList() { dummyHead = new Node(); size = 0; } // Gets the number of elements in the linked list public int getSize(){ return size; } // Returns whether the linked list is empty public boolean isEmpty(){ return size == 0; } // Add a new element to the linked list header e public void addFirst(E e){ add(0, e); } // Add a new element at the end of the linked list e public void addLast(E e){ add(size, e); } // In the linked list index(0-based)Add new element to location e // It is not a common operation in the linked list. Practice with:) public void add(int index, E e){ if(index < 0 || index > size) throw new IllegalArgumentException("Add failed. Illegal index."); Node prev = dummyHead; for(int i = 0 ; i < index ; i ++) prev = prev.next; // Node node = new Node(e); // node.next = prev.next; // prev.next = node; prev.next = new Node(e, prev.next);//More elegant writing size++; } // Get the first element of the linked list public E getFirst(){ return get(0); } // Get the last element of the linked list public E getLast(){ return get(size - 1); } // Get the second page of the linked list index(0-based)Elements in multiple locations // It is not a common operation in the linked list. Practice with:) public E get(int index){ if(index < 0 || index >= size) throw new IllegalArgumentException("Get failed. Illegal index."); Node cur = dummyHead.next; for(int i = 0 ; i < index ; i ++) cur = cur.next; return cur.e; } // Modify the second page of the linked list index(0-based)The element at position is e // It is not a common operation in the linked list. Practice with:) public void set(int index, E e){ if(index < 0 || index >= size) throw new IllegalArgumentException("Set failed. Illegal index."); Node cur = dummyHead.next; for(int i = 0 ; i < index ; i ++) cur = cur.next; cur.e = e; } // Find whether there are elements in the linked list e public boolean contains(E e){ Node cur = dummyHead.next; while(cur != null){ if(cur.e.equals(e)) return true; cur = cur.next; } return false; } // Delete the first element from the linked list, Returns the deleted element public E removeFirst(){ return remove(0); } // Deletes the last element from the linked list, Returns the deleted element public E removeLast(){ return remove(size - 1); } // Delete from linked list index(0-based)Element of location, Returns the deleted element // It is not a common operation in the linked list. Practice with:) public E remove(int index){ if(index < 0 || index >= size) throw new IllegalArgumentException("Remove failed. Index is illegal."); Node prev = dummyHead; for(int i = 0 ; i < index ; i ++) prev = prev.next; Node retNode = prev.next; prev.next = retNode.next; retNode.next = null; size --; return retNode.e; } // Delete element from linked list e public void removeElement(E e){ Node prev = dummyHead; while(prev.next != null){ if(prev.next.e.equals(e)) break; prev = prev.next; } if(prev.next != null){ Node delNode = prev.next; prev.next = delNode.next; delNode.next = null; size --; } } private class Node{ public E e; public Node next; public Node() { this(null, null); } public Node(E e) { this(e, null); } public Node(E e, Node next) { this.e = e; this.next = next; } @Override public String toString() { return e.toString(); } } @Override public String toString(){ StringBuilder res = new StringBuilder(); //The first traversal method // Node cur = dummyHead.next; // while(cur != null){ // res.append(cur + "->"); // cur = cur.next; // } //The second traversal method for(Node cur = dummyHead.next ; cur != null ; cur = cur.next) res.append(cur + "->"); res.append("NULL"); return res.toString(); } }
//No version with virtual header public class LinkedList2<E> { private Node head; private int size; public LinkedList2() { head = null; size = 0; } // Gets the number of elements in the linked list public int getSize(){ return size; } // Returns whether the linked list is empty public boolean isEmpty(){ return size == 0; } // Add a new element to the linked list header e public void addFirst(E e){ // Node node = new Node(e); // node.next = head; // head = node; head = new Node(e,head);//More elegant writing size ++; } // In the linked list index(0-based)Add new element to location e // It is not a common operation in the linked list. Practice with:) public void add(int index, E e){ if(index < 0 || index > size) throw new IllegalArgumentException("Add failed. Illegal index."); if(index == 0) addFirst(e); else{ //Add elements to the middle Node prev = head; for(int i = 0 ; i < index - 1 ; i ++) prev = prev.next; // Node node = new Node(e); // node.next = prev.next; // prev.next = node; prev.next = new Node(e, prev.next);//More elegant writing size++; } } // Add a new element at the end of the linked list e public void addLast(E e){ add(size, e); } private class Node{ public E e; public Node next; public Node() { this(null, null); } public Node(E e) { this(e, null); } public Node(E e, Node next) { this.e = e; this.next = next; } @Override public String toString() { return e.toString(); } } }
1. New file:
Let's go back to the previous linked list project and create a new file:
2. Copy the unchanged Code:
2,add,addFirst,addLast:
First recall the method definitions related to adding non recursive methods:
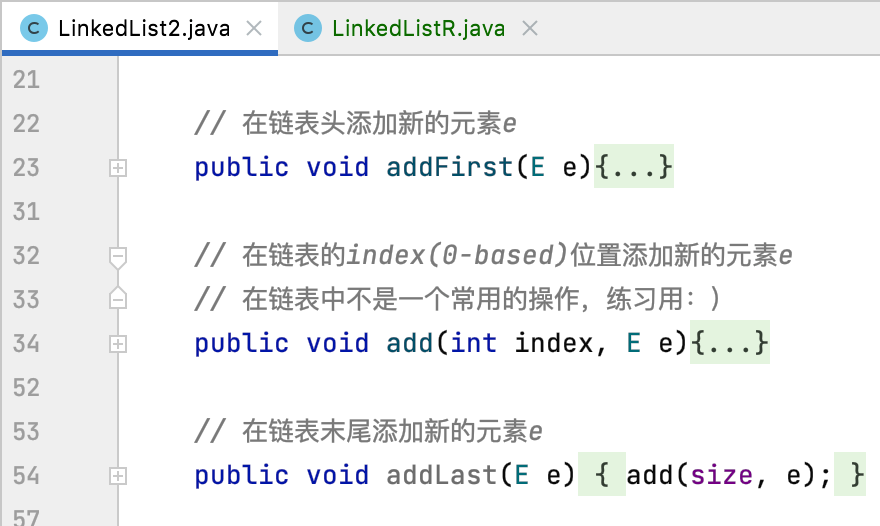
The core is the implementation of the logic of add(), because both addFirst and addLast actually call it. Let's define it first:
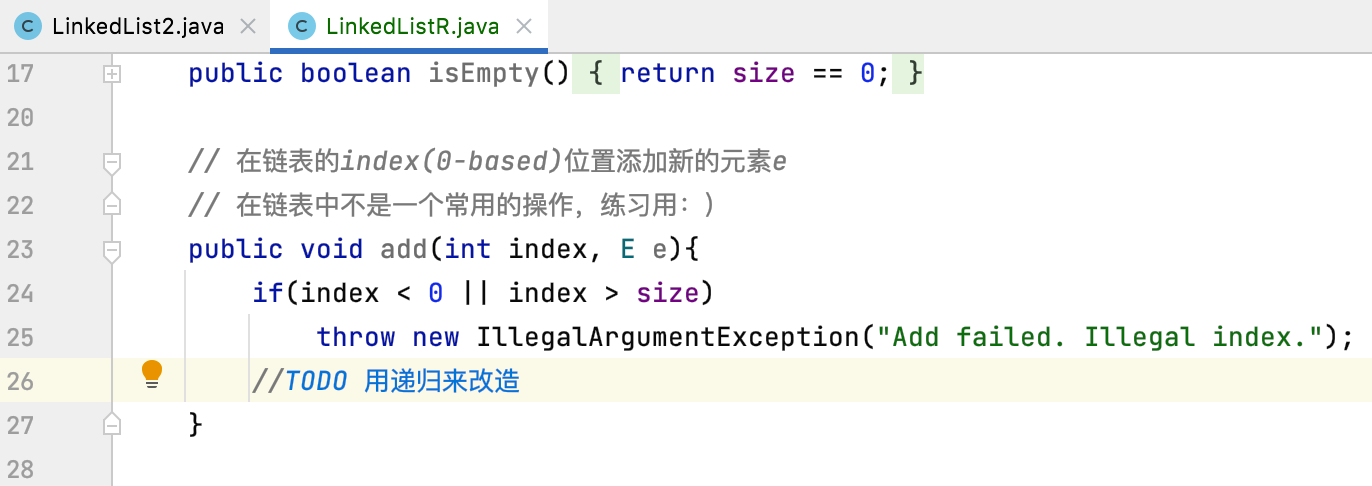
add():
How to transform it with delivery? According to the natural nature of linked list recursion:

Obviously, a separate method needs to be defined to make recursive calls, as follows:
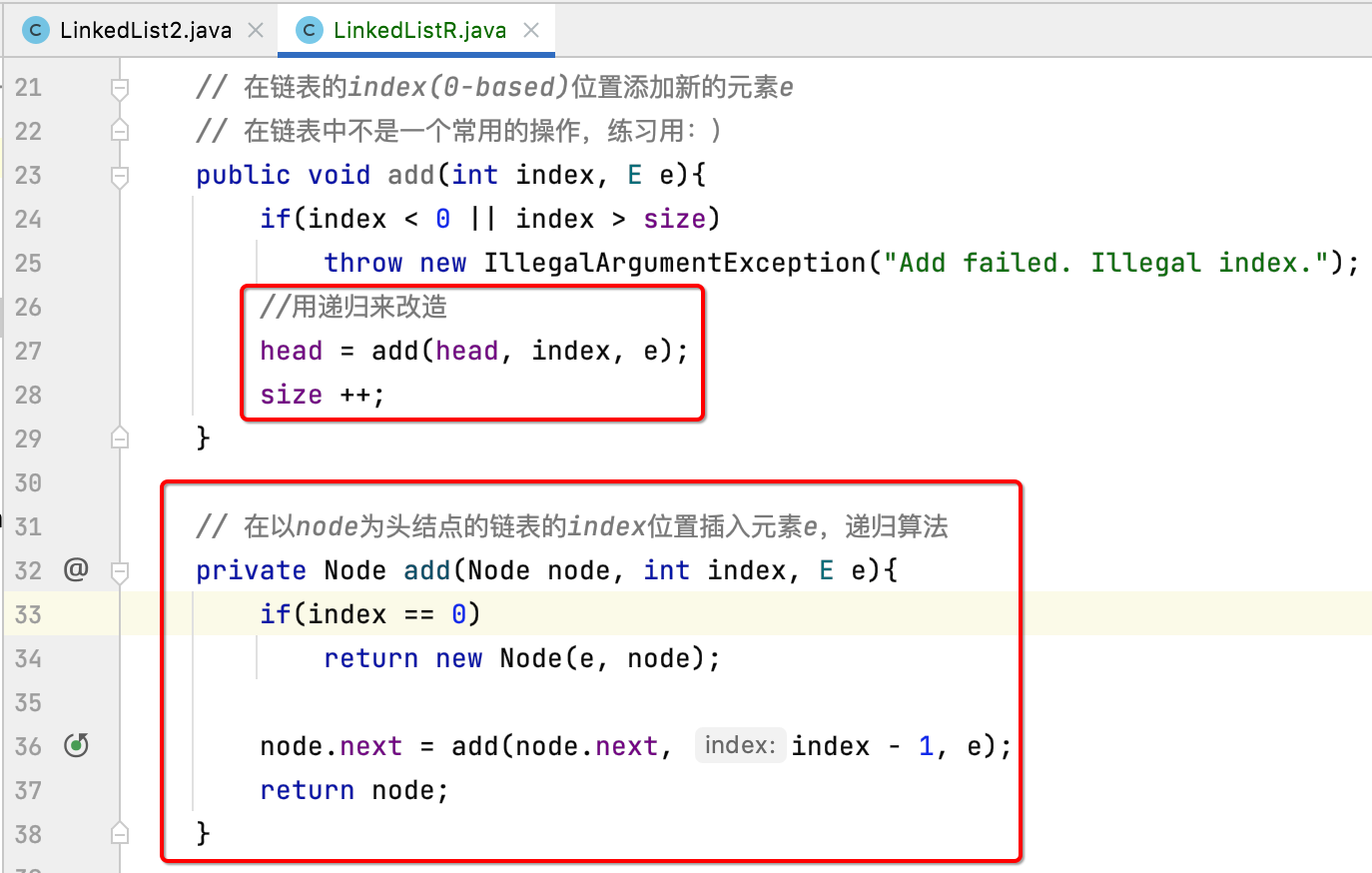
If the writing method of recursion is not clear, you can also use the debugging method mentioned above to debug and understand. There is no more explanation here. Pay attention to a small detail. We use private for the design of recursive functions, and the add() method actually called is public. The purpose of this design is that recursive functions need to use the "Node" class, For external users, they cannot perceive the existence of the "Node" class, so they declare the recursive function private.
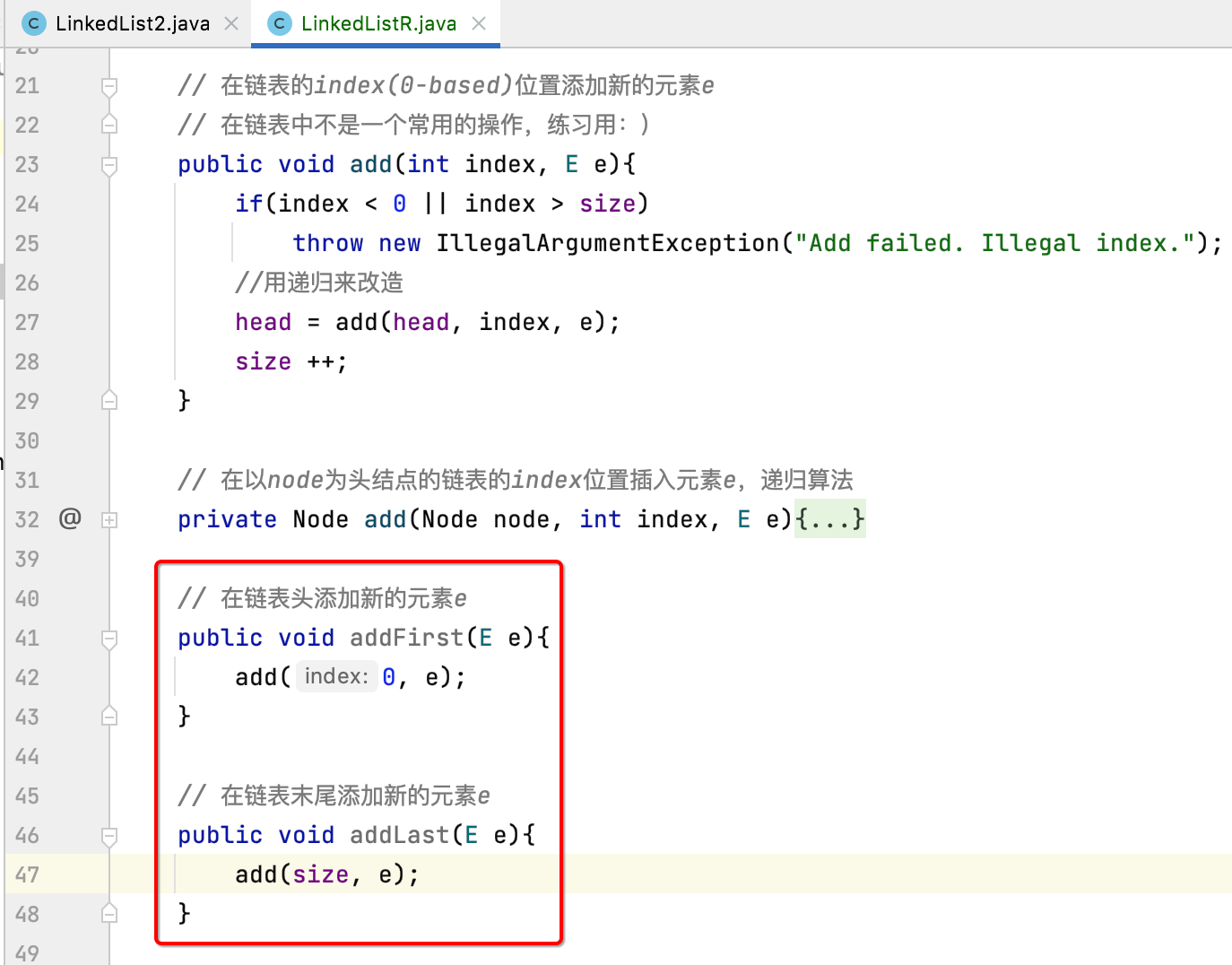
addFirst(),addLast():
The implementation of these two methods is relatively simple:
3,get,getFirst,getLast:
Similarly, let's recall the non recursive implementation of get related methods:
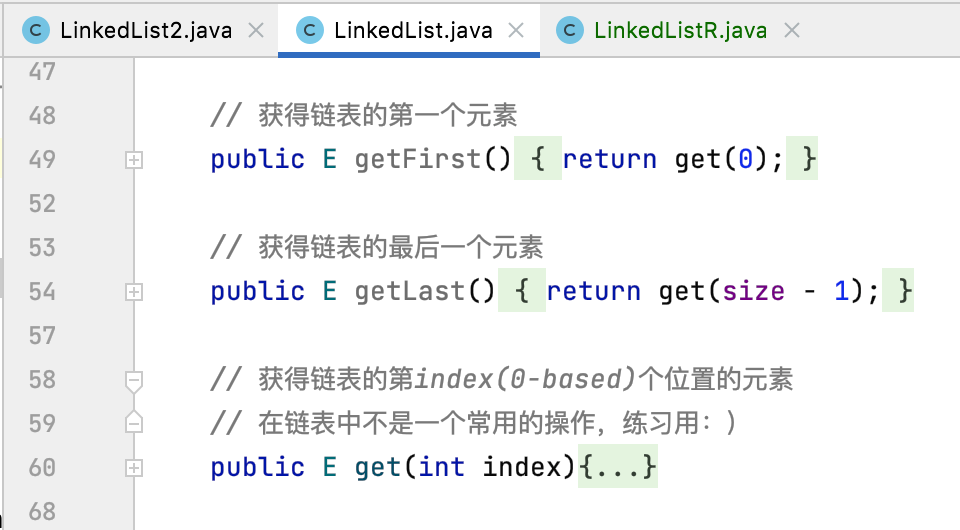
The same core is the implementation of the get() method.
get():
Since recursion is used, the recursive function must be designed, right? So the overall transformation is as follows:
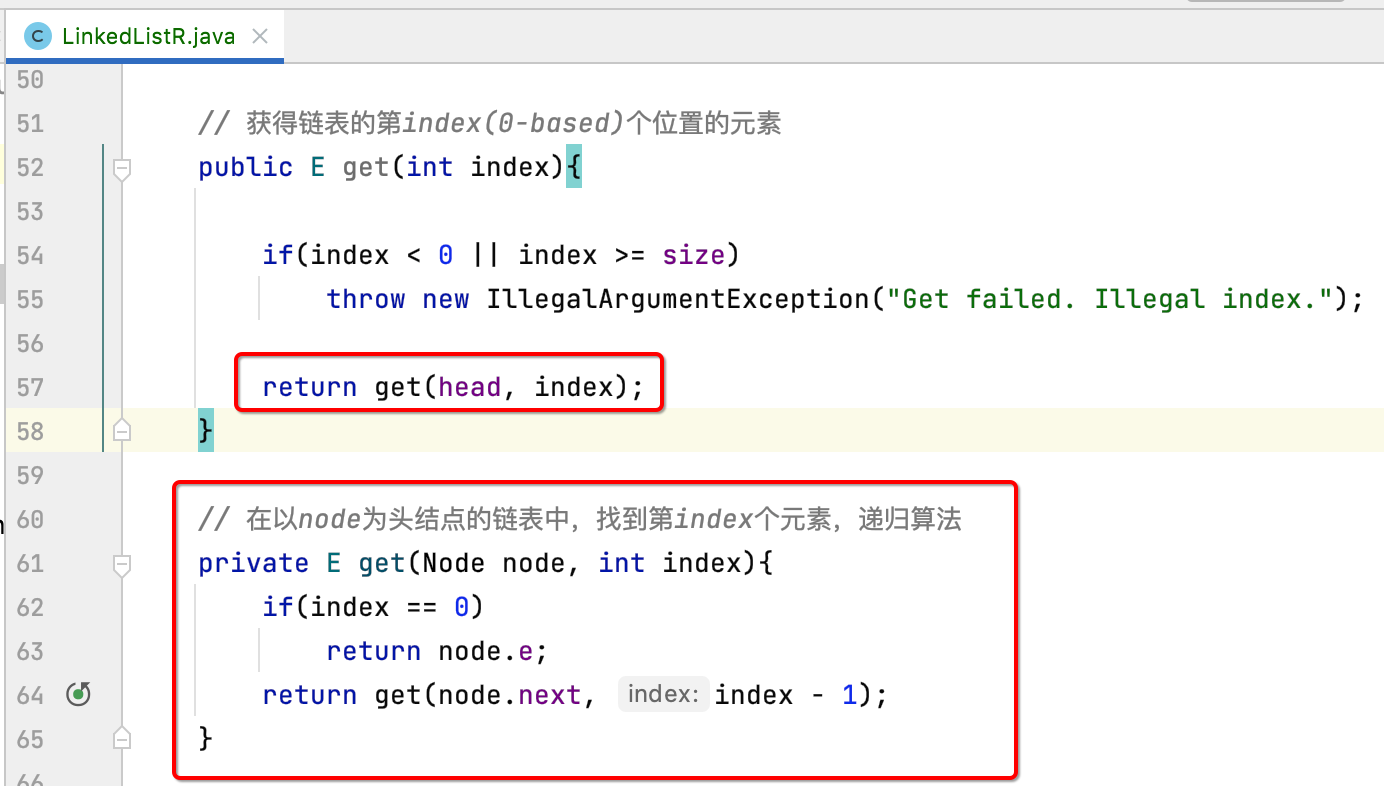
It has been found that the design of recursive functions for linked lists will have a Node parameter and an index parameter.
getFirst(),getLast():
It's simple for these two:
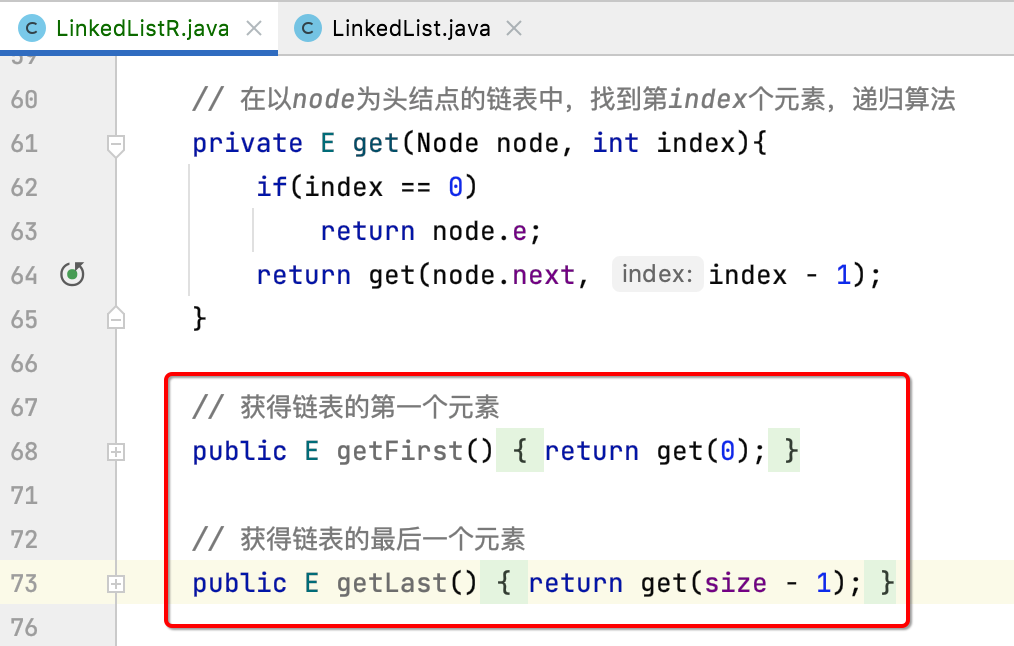
4,set:
Next, modify the element at the specified position in the linked list. The recursive transformation is as follows:
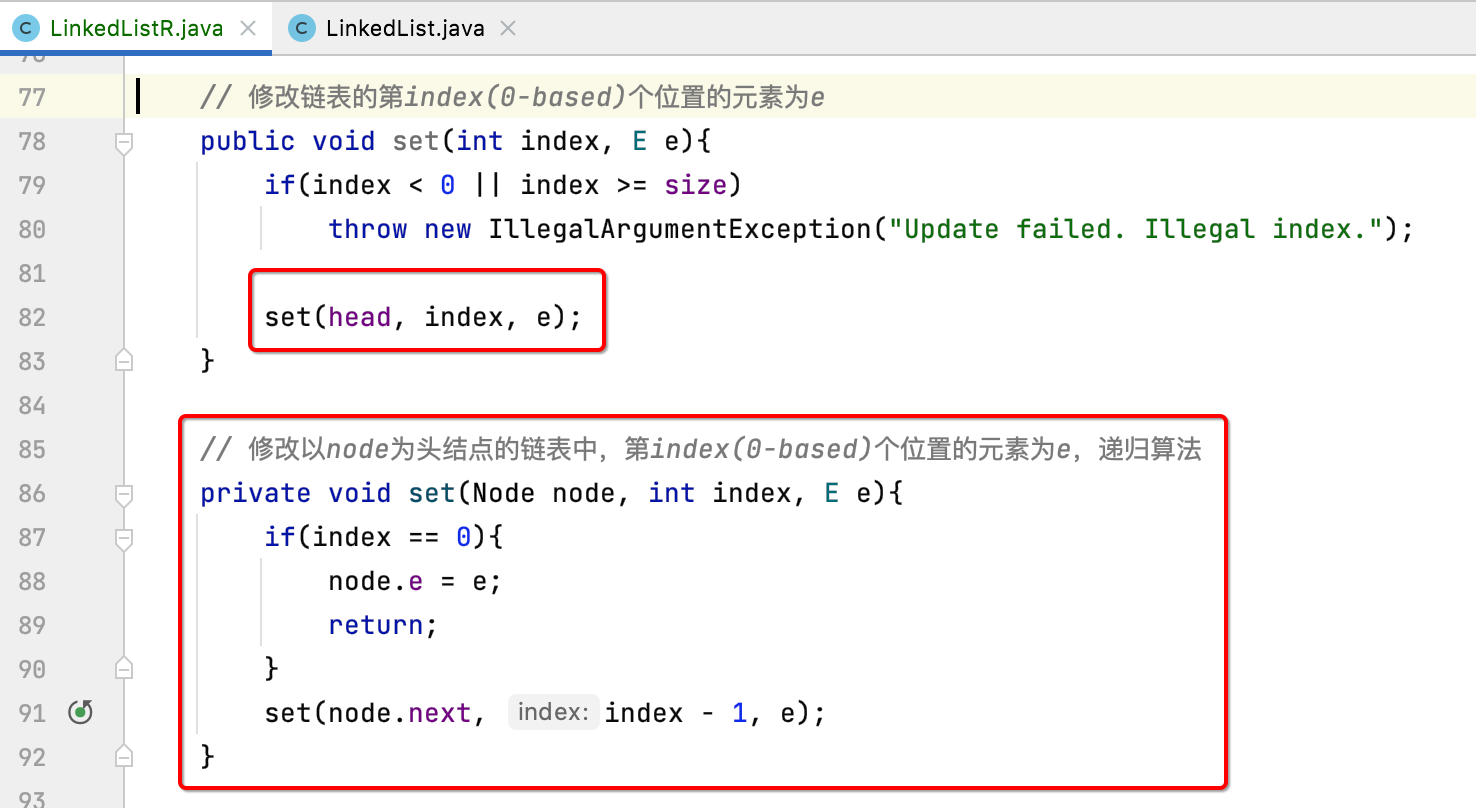
5,contains:
It also needs to be changed to recursion, as follows:
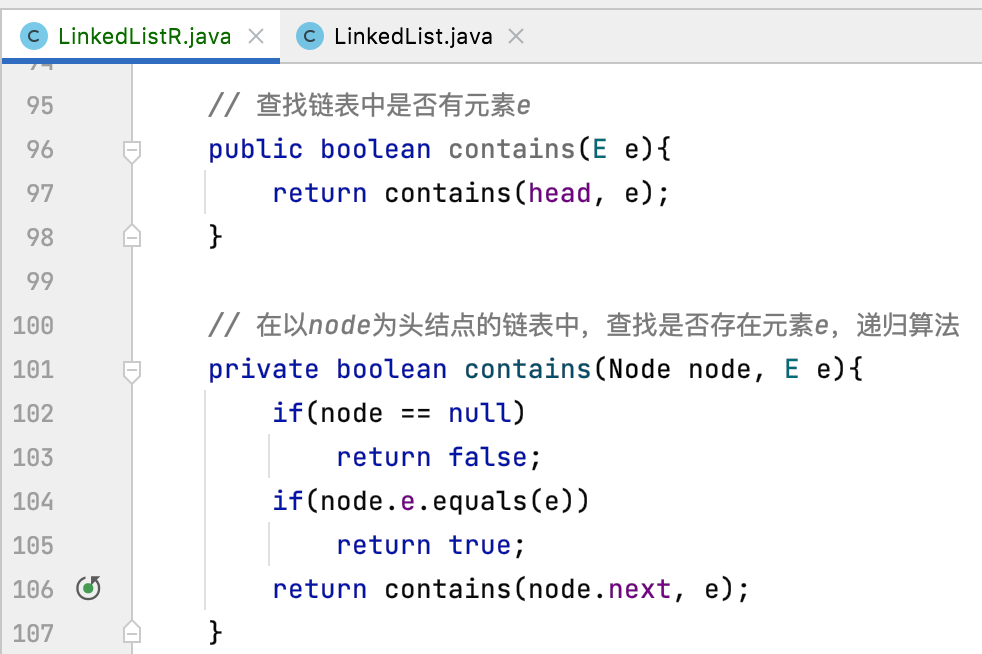
6,remove,removeFirst,removeLast:
Recall the previous definitions related to non recursive methods:
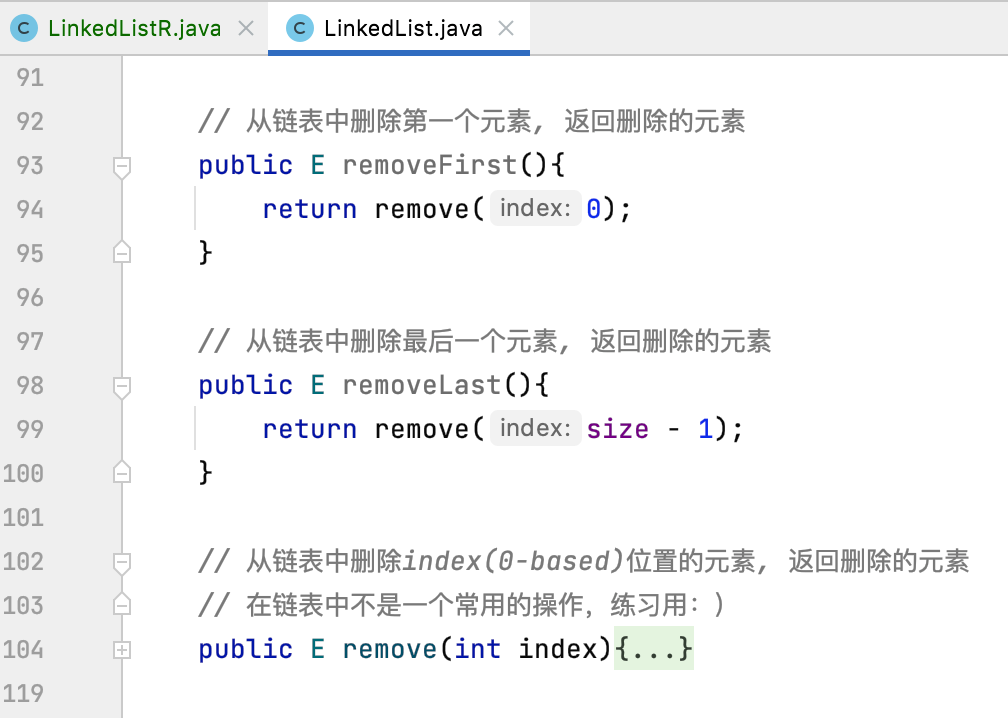
Its core is the method of remove().
remove():
Change to recursion as follows:
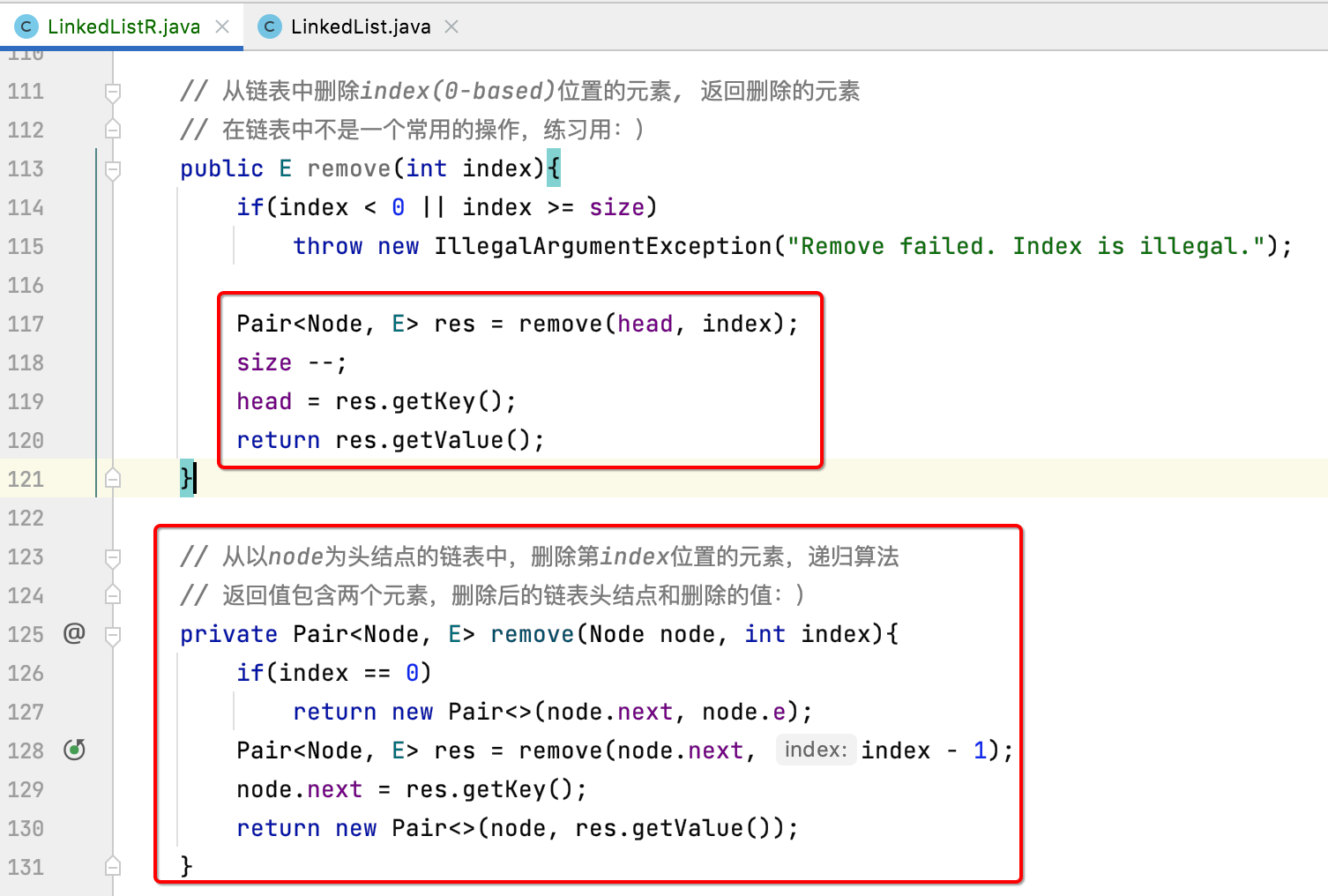
It may not be well understood about this. Similarly, you can debug and track it.
removeFirst(),removeLast():
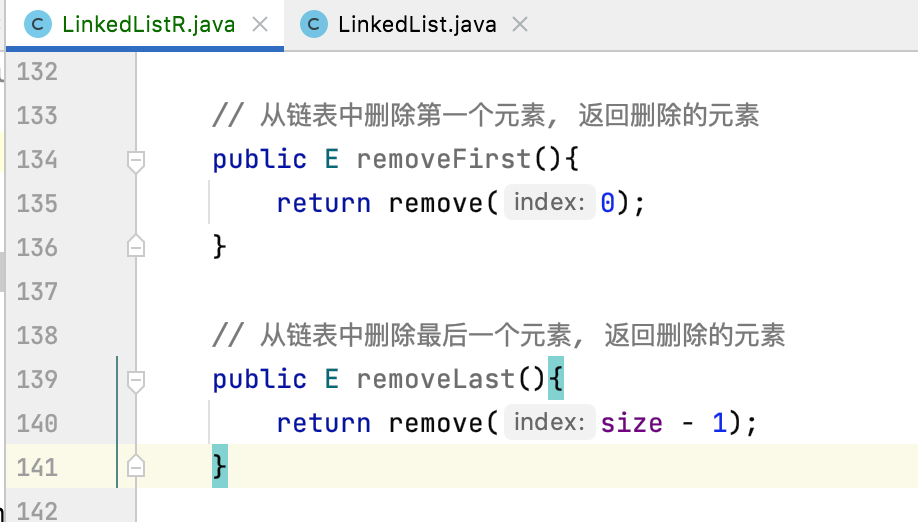
7,removeElement:
We have implemented this with recursion before, and there is no more explanation here:
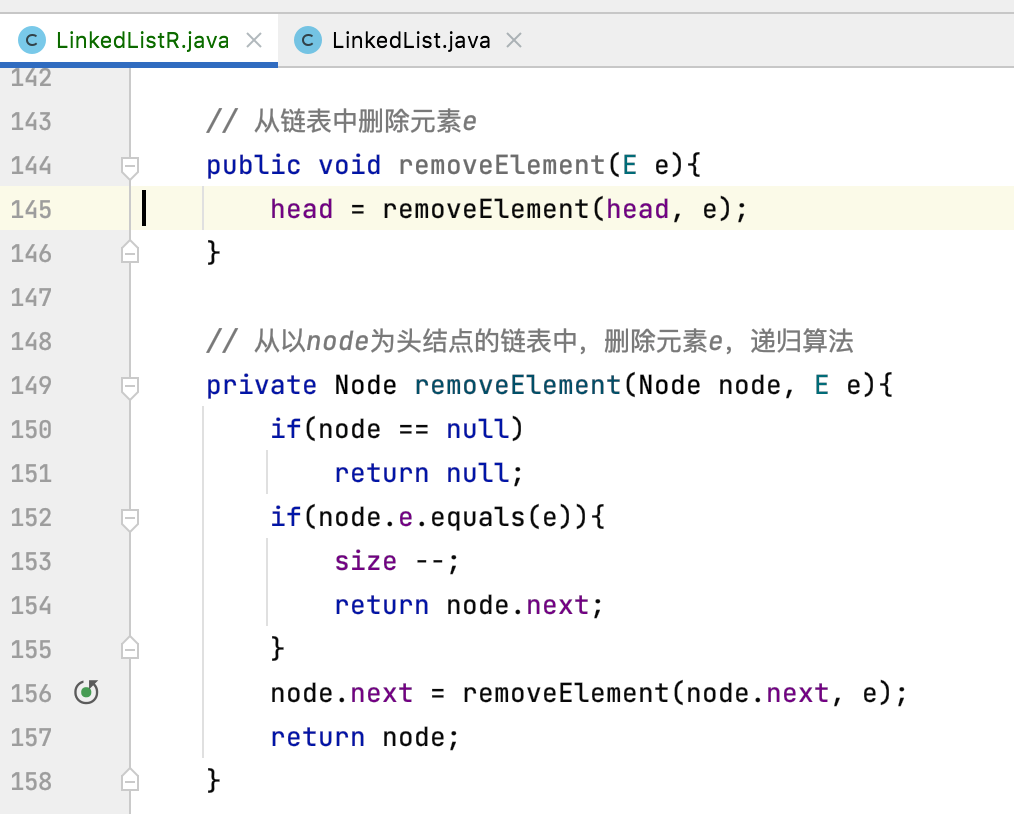
8. Test:
Finally, let's test:
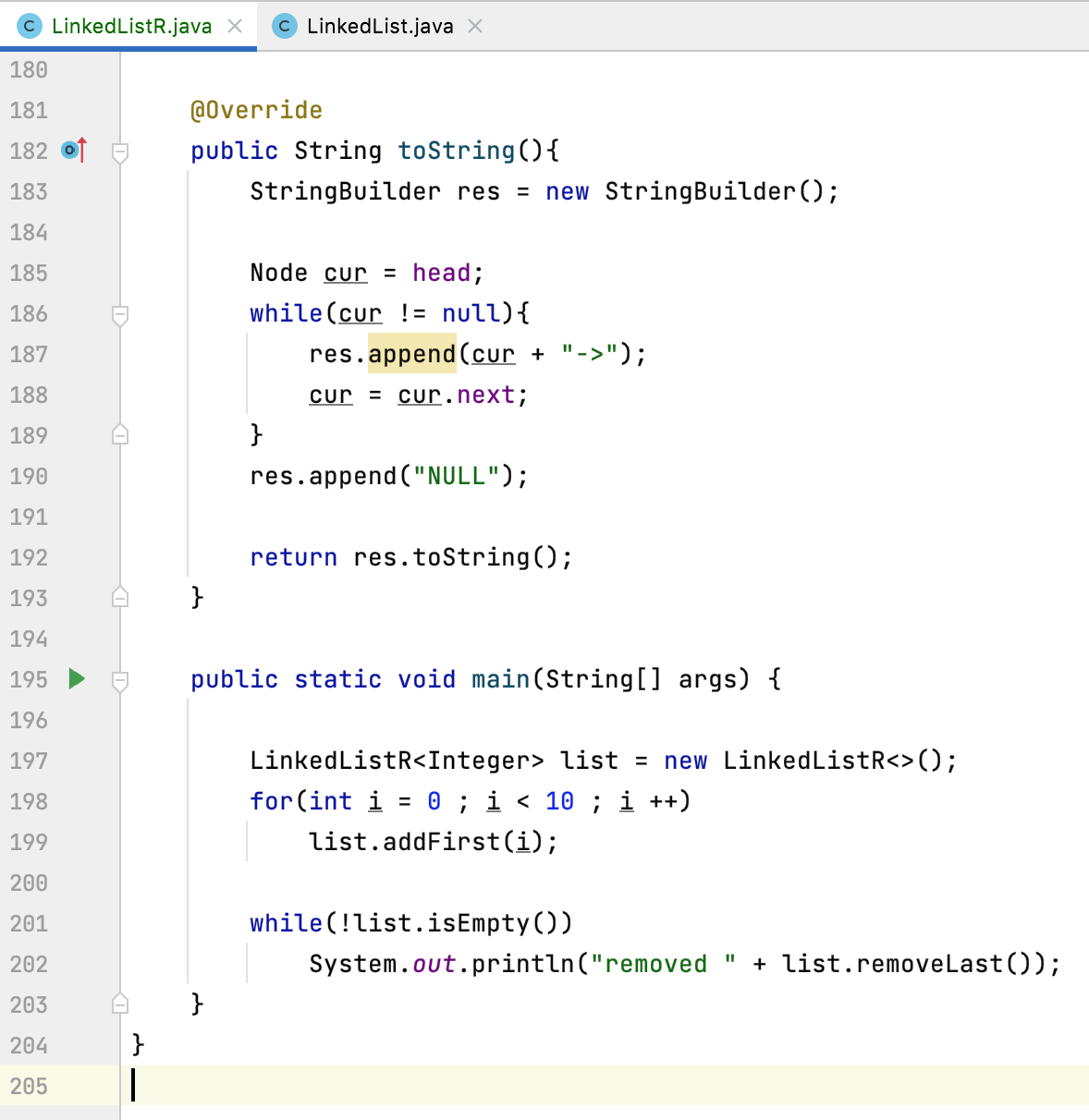
function:
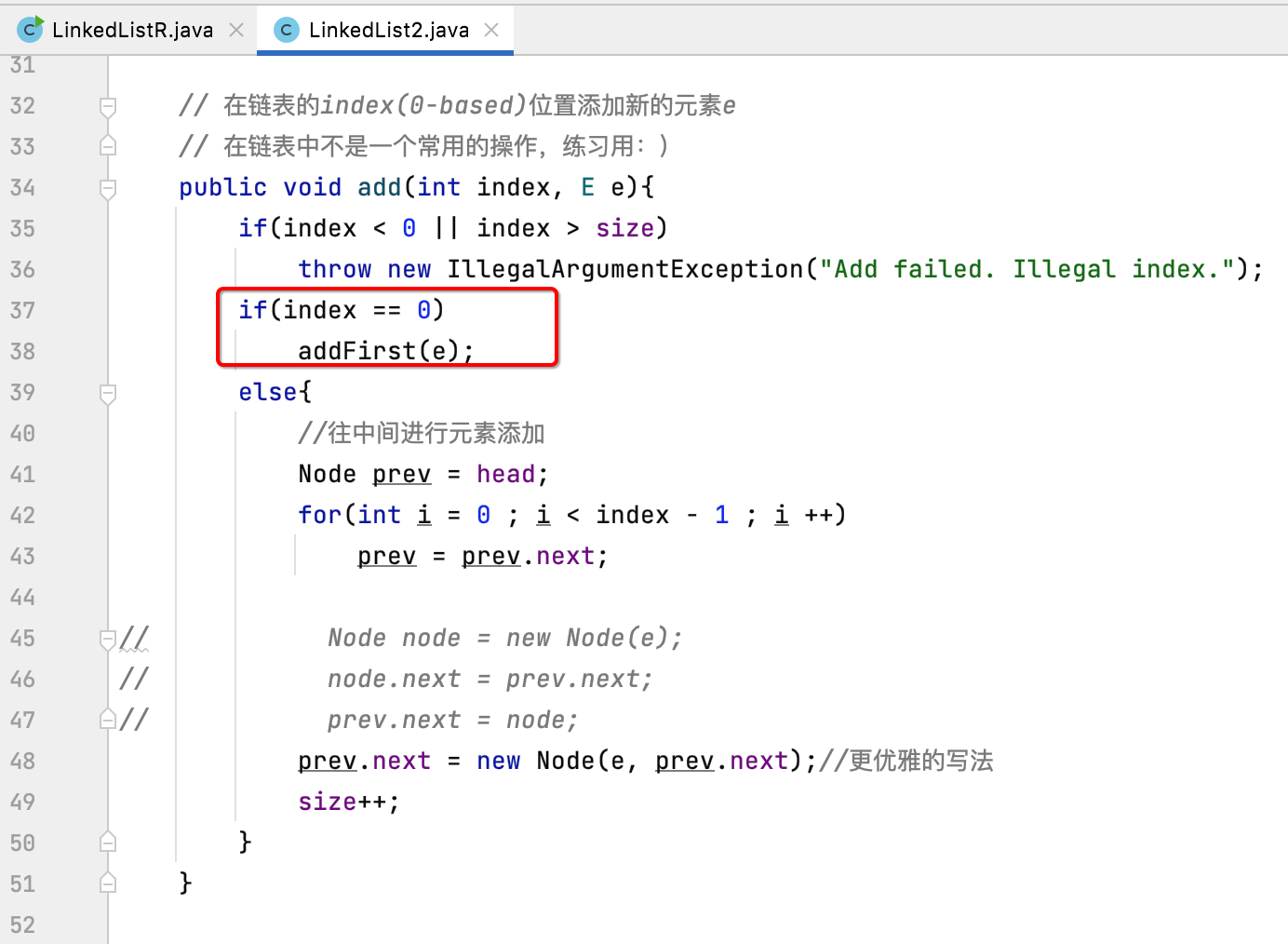
There is one detail you have found. After using recursion, you do not need to use the virtual head node at all, and it is also a unified behavior in dealing with the problem of position 0. For example, when we did not use the virtual head node to add elements before, we made some more judgments that the position is 0:
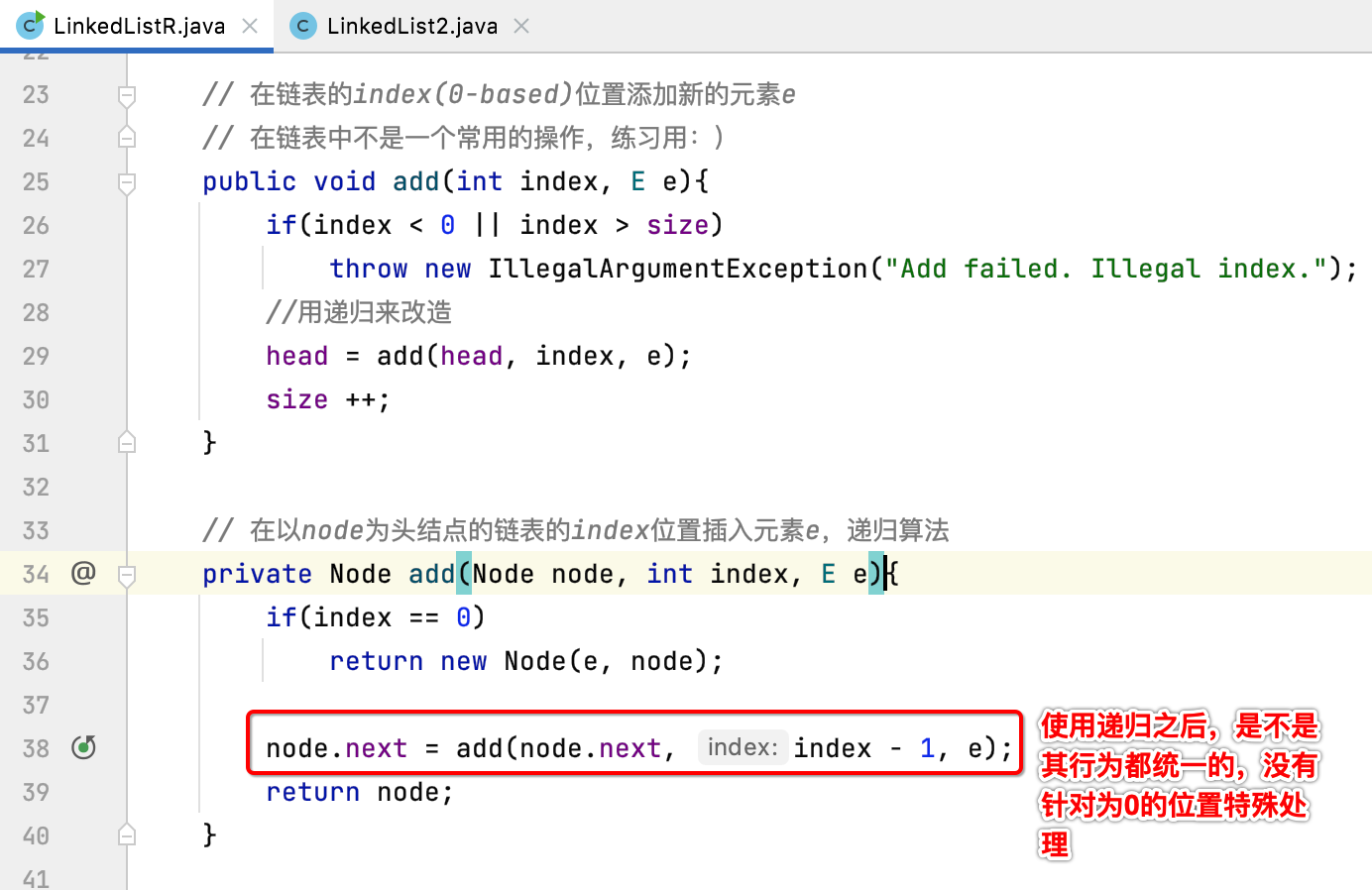
Discussion on the return value of linked list recursive algorithm:
On the recursive implementation of linked list, to be honest, it is not so easy to transform. In the actual transformation, you may encounter the following two problems more or less. Here, analyze these two problems.
Question 1: can the removeElements recursive function not return a value?
For the program we previously implemented to delete the specified elements in the linked list:

If we don't return ListNode in this recursive function, do you think we can achieve the same effect of recursively deleting elements? The answer is no, because the result of each recursion needs to be linked with the previous linked list again. Why? Because there is this sentence:

If the recursive function does not return a value, do you think it can be linked to the previous linked list?
Question 2: can the add recursive function not return a value?
Remember the code we used to implement add in linked list recursion?

For the recursive method add, can you also not return the value Node? That is to say:

Obviously, it is not allowed. There is also the problem that the recursive linked list needs to be connected with the previous linked list, right? Next, let's see why it is not possible to write this:
Do not return Node analysis:
For example, a linked list:
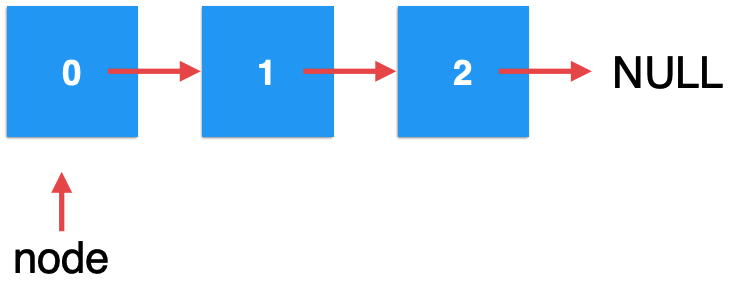
We want to insert an element e into the position of 1. We don't care about the specific value of e. at this time, we recurse from the position 0. Obviously, the node at this time is not the position we want to insert, and the recursive function will execute this:
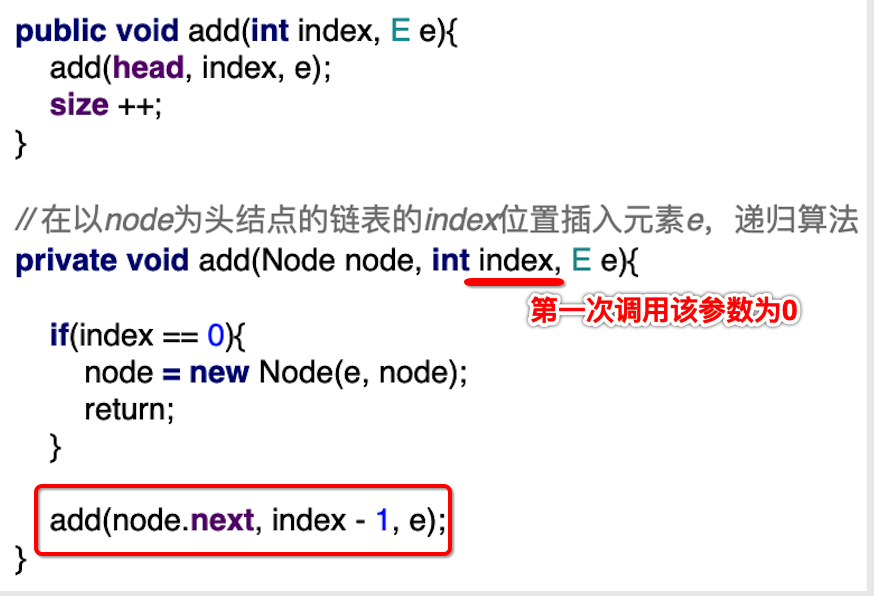
At this time, recursion is performed again, and the node at this time is at this position:
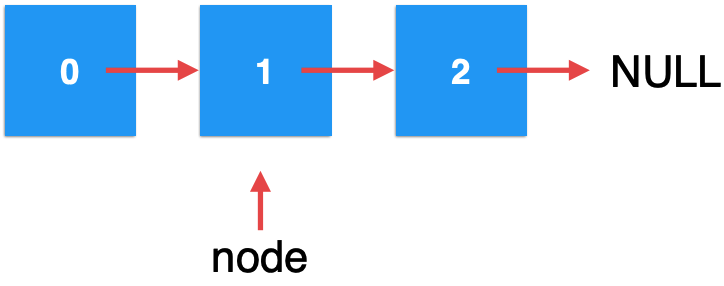
When index=0, this condition will be entered:
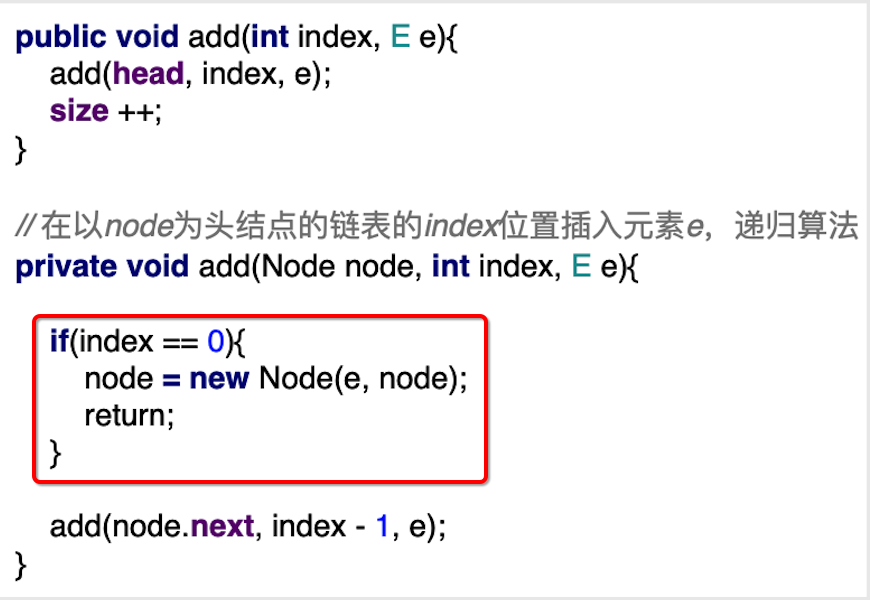
The memory changes to:
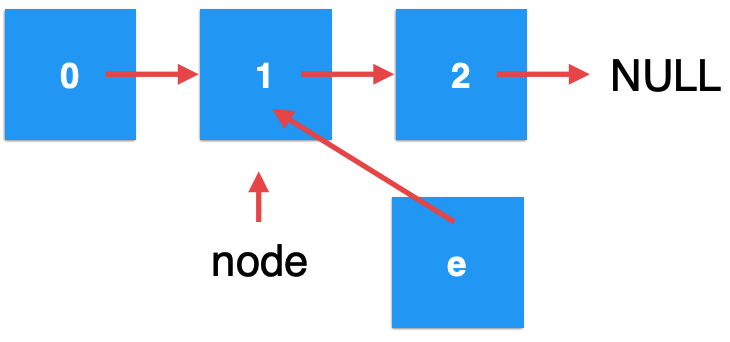
Since the node parameter is assigned, the node at this time points to:
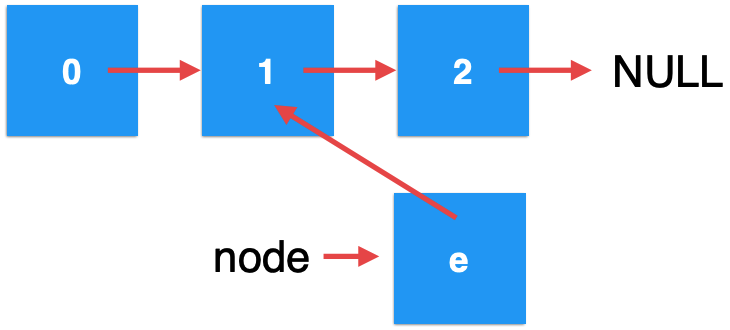
OK, then we return:

Since the node parameter is a formal parameter, that is, a temporary variable, its life cycle disappears when the function returns. Therefore, the point of node is gone. When it returns to the recursive function call of the previous layer, the form changes to:
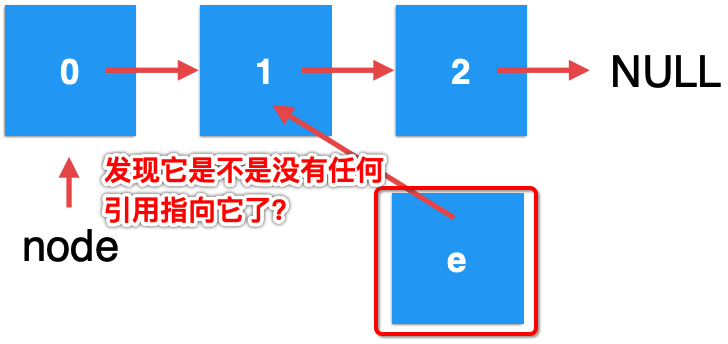
Here's the key point. Since the newly developed element e wood is referenced by any reference, it will obviously be recycled according to the JVM garbage collection mechanism, so you will finally find that after the add operation:
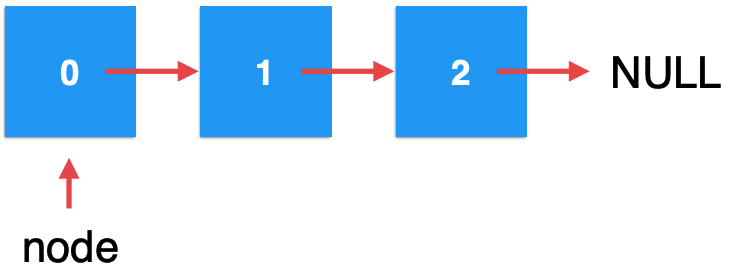
In fact, the element was not successfully added to the linked list, which is why void cannot be returned here.
Return Node analysis:
Next, compare and analyze our correct code to see why recursion is designed to return Node, and it can be normal when adding elements?
Take this linked list as an example:
The first call, index=0, so the form is:
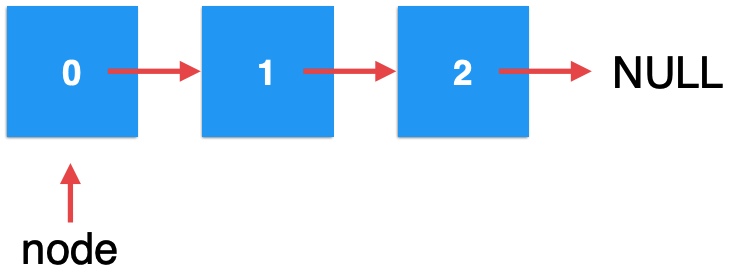
Then call the second recursion. At this time, the index=0, so:
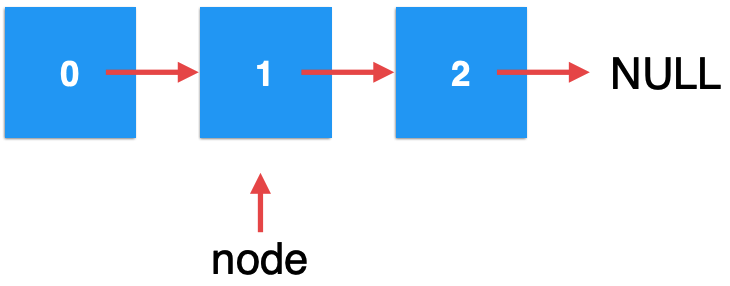
At this point, you will enter the condition of recursive method:

Therefore, the newly created element points to the current node, so it is:
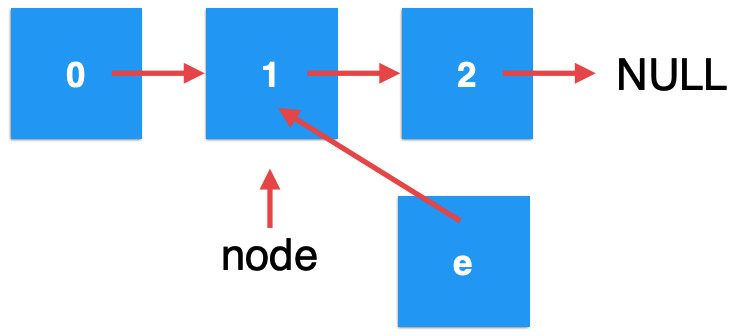
The key is to return it. At this time, it will return to the code of the last recursion:

After returning, the form becomes:
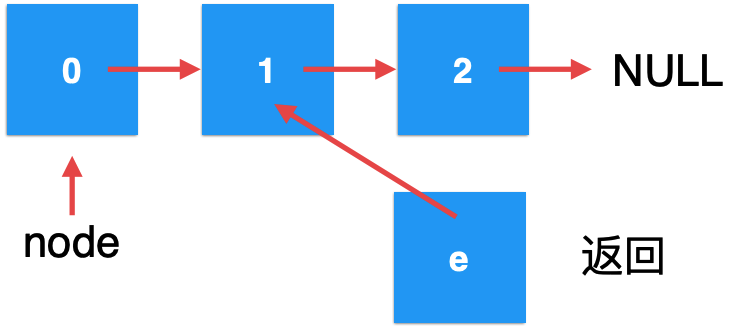
And because of node Next points to the linked list of e elements we just created. It is obvious that the form will eventually change to:
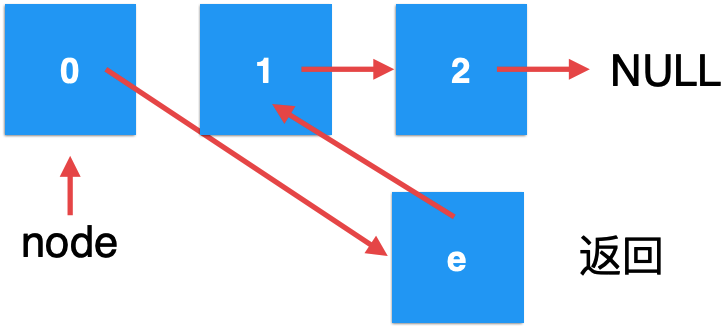
The final procedure is executed to this point:

The final linked list is:
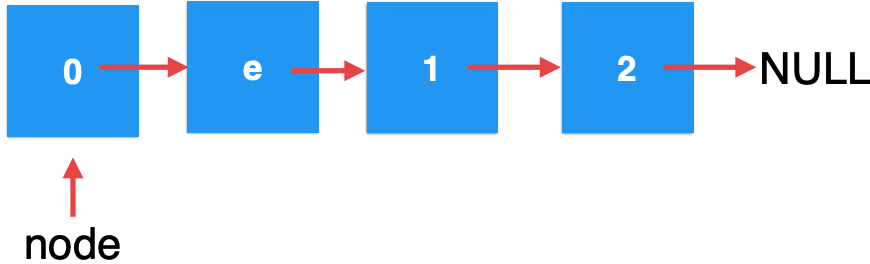
Summary:
Through such a comparison, is the understanding of linked list recursion further? The meaning of the return value must be clear.
More topics related to linked lists:
Stanford document description:

Various other forms of linked lists:
Double linked list:
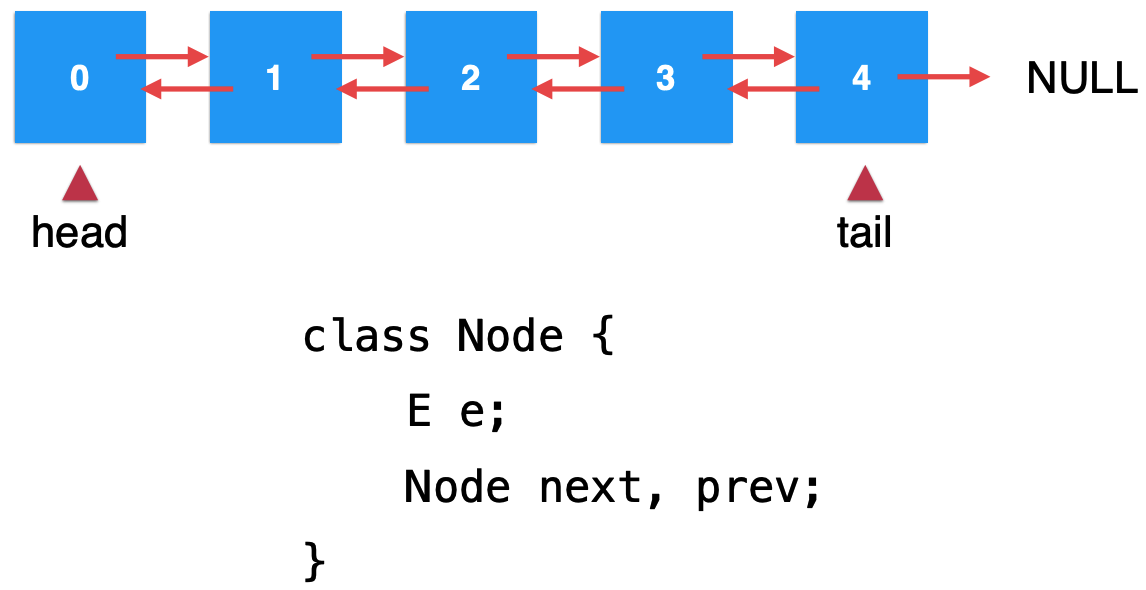
Circular linked list:
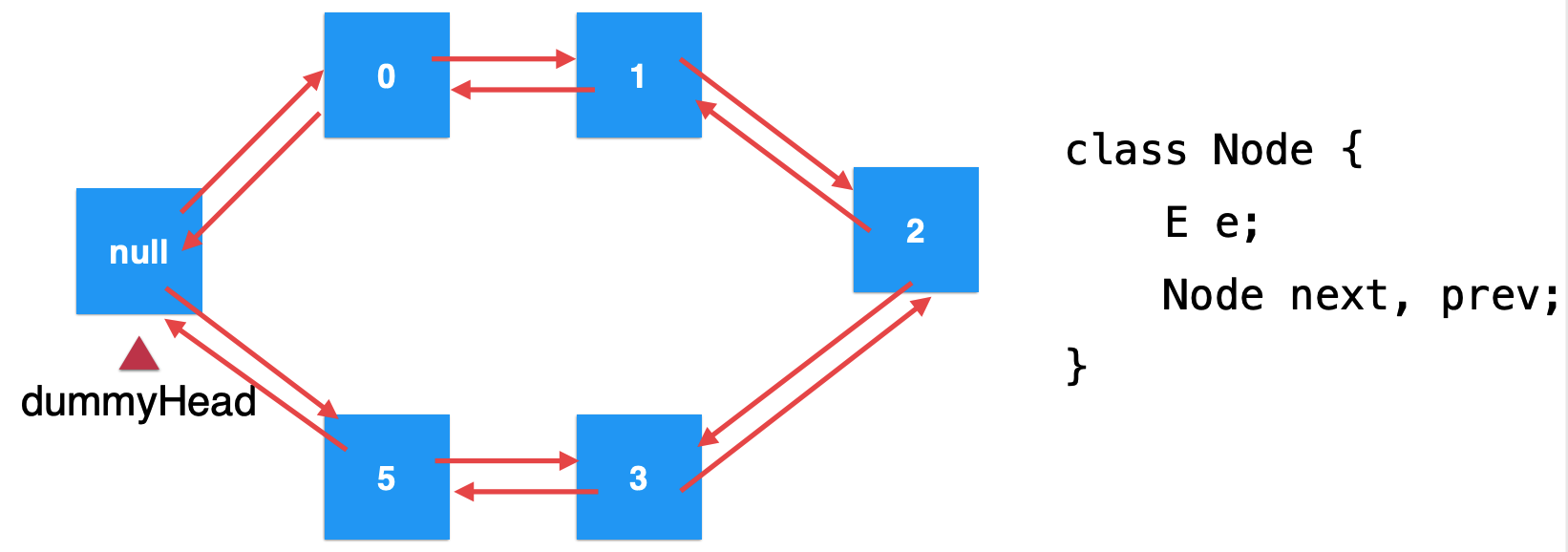
Array linked list:
If we add an index attribute when storing elements, we can build a linked list data structure, such as: