1, Representation of complex numbers

In previous articles, I once had a question, that is, how does scheme language realize polymorphism? No, the book seems to give us the answer to this question soon.

We know that the plural number can be expressed in two ways:

1. Representation of rectangular coordinate system
Real part( z 1 + z 2 z_1+z_2 z1 + z2) = real part( z 1 z_1 z1) + real part( z 2 z_2 z2​)
Imaginary part( z 1 + z 2 z_1+z_2 z1 + z2) = imaginary part( z 1 z_1 z1) + imaginary part( z 2 z_2 z2​)

2. Polar coordinate system representation
Mold( z 1 + z 2 z_1+z_2 z1 + z2) = imaginary part( z 1 z_1 z1) + imaginary part( z 2 z_2 z2​)
Argument( z 1 + z 2 z_1+z_2 z1 + z2) = amplitude( z 1 z_1 z1) + argument( z 2 z_2 z2​)

We can show two representations in one diagram:

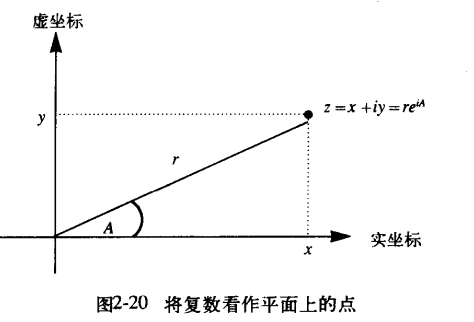
In fact, in most cases, programmers tend to use rectangular coordinate system representation rather than polar coordinate system representation, because of the rounding error between rectangular coordinate system and polar coordinate system representation. But the example of plural representation can let us understand how to design and implement the program of general operation concisely and clearly.

For the above two representations, We can use the method of programming according to the desire to write the following two procedures to construct a complex number (the desire is that if we have four selection functions: real part to obtain the real part under the representation of rectangular coordinate system, imag part to obtain the imaginary part, magnitude to obtain the module length and angle to obtain the argument under the representation of polar coordinate system):

1. Complex number in rectangular coordinate system:

(make-from-real-imag (real-part z) (imag-part z))

2. Complex number in polar coordinate system:

(make-from-mag-ang (magnitude z) (angle z))

Try to translate the above two processes into Chinese:

1. Complex number in rectangular coordinate system:

(Constructing complex numbers in Cartesian coordinates (Real part complex) (Imaginary complex))

(Construct a complex number (real complex number) (imaginary complex number) from the real part and imaginary part

2. Complex number in polar coordinate system:

(Constructing complex numbers in polar coordinates (Modular complex) (Argument complex))

(Construct complex number according to module length and argument (module length complex number) (argument complex number))

With the above constructor and selection function, we can use code to describe the four basic processes of addition, subtraction, multiplication and division based on complex numbers (addition and subtraction are described by rectangular coordinate system method, multiplication and division are described by polar coordinate system method)

(define (add-complex z1 z2)
    (make-from-real-imag (+ (real-part z1) (real-part z2))
                         (+ (imag-part z1) (imag-part z2))))
(define (sub-complex z1 z2)
    (make-from-real-imag (- (real-part z1) (real-part z2))
                         (- (imag-part z1) (imag-part z2))))
(define (mul-complex z1 z2)
    (make-from-mag-ang (* (magnitude z1) (magnitude z2))
                       (+ (angle z1) (angle z2))))
(define (div-complex z1 z2)
    (make-from-mag-ang (/ (magnitude z1) (magnitude z2))
                       (- (angle z1) (angle z2))))

Try to translate the above process into Chinese:

(Definition (plural addition plural a plural b)
    (Constructing complex numbers in rectangular coordinates(+ (Real part plural a) (real part plural b)
                         (+ (Imaginary part complex a) (imaginary part complex B))
(Definition (plural subtraction plural a plural b)
    (Constructing complex numbers in rectangular coordinates(- (Real part plural a) (real part plural b)
                         (- (Imaginary part complex a) (imaginary part complex B))
(Definition (complex multiplication complex a complex B)
    (Constructing complex numbers in polar coordinates(* (Module length complex a) (module length complex B))
                        (+ (Argument plural a) (argument plural b))
(Definition (plural division plural a plural b)
    (Constructing complex numbers in polar coordinates(/ (Module length complex a) (module length complex B))
                        (- (Argument plural a) (argument plural b))

In addition, we can also write the process function of the transformation between the two complex representation methods according to the trigonometric function formula of the transformation between the two complex representation methods:
x = r c o s A r = x 2 + y 2 y = r s i n A A = a r c t a n ( y , x ) x = rcosA \qquad r = \sqrt {x^2 + y^2} \\ \quad y = rsinA \qquad A=arctan(y,x) x=rcosAr=x2+y2 ​y=rsinAA=arctan(y,x)
while, I think if the above formula is translated into Chinese, it can be written as follows:
real Department = model long ⋅ more than string ( Breadth horn ) model long = real Department 2 + empty Department 2 empty Department = model long ⋅ just string ( Breadth horn ) Breadth horn = back just cut ( empty Department ， real Department ) Real part = module length \ cdot cosine (argument) \ qquad module length = \ sqrt {real part ^ 2 + imaginary part ^ 2} \ \ \ \ Quad imaginary part = module length \ cdot sine (argument) \ qquad argument = arctangent (imaginary part, real part) Real part = module length ⋅ cosine (argument) module length = real part 2 + imaginary part 2 Imaginary part = module length ⋅ sine (argument) argument = arctangent (imaginary part, real part)

I think the name "anyway cut" still seems to be a little less concise. I was wondering whether to directly adopt the name "inclination"? (in English, arc means arc, so objectively compare arctan with the Chinese translation of "arctangent". The former is more vivid. I hope to find a very vivid description in Chinese, but there are not too many occurrences in the meaning of "angle" in ancient China. Even in ancient China, it can be said that there is no concept of "angle" in modern mathematics In ancient times, this word did not have today's mathematical meaning. It once had the potential to develop into the concept of angle in modern mathematics. There is a saying called "Yu", in which the word "Yu" means obtuse angle and "Yu" means acute angle. The two are combined into the bending degree of broken line, but to be honest, I still can't think of any simplicity from this term, Another translation of arctan Through reading and thinking, it seems difficult for me to give a concise and vivid description in Chinese for the time being?

HMM... in fact, I think tangent angle, sine angle and cosine angle are a fairly good description method? But there is still one more word, which is not concise enough.
Of course, if you don't mind talking about it, there are such things as "finding angles from tangents", but of course it's not good, and it's too long, for a commonly used mathematical function.
Here is an article about the naming of trigonometric functions: https://zhuanlan.zhihu.com/p/56285253

The first is a process of selecting rectangular coordinates, that is, the real part and imaginary part are straightforward, but the module and argument need to be obtained according to the triangular relationship:

(define (real-part z) (car z))

(define (imag-part z) (cdr z))

(define (magnitude z)
    (sqrt (+ (square (real-part z)) (square (imag-part z)))))

(define (angle z)
    (atan (imag-part z) (real-part z)))

(define (make-from-real-imag x y) (cons x y))

(define (make-from-mag-ang r a)
    (cons (* r (cos a)) (* r (sin a))))

Try to translate the above process into Chinese:

(Definition (real part plural) (preceding plural))

(Definition (imaginary part complex number) (subsequent complex number))

(Definition (module length and complex number)
    (Prescription(+ (Square (real part complex number)) (square (imaginary part complex number))

(Definition (argument complex)
    (Arctangent (imaginary part complex number) (real part imaginary part))

(Definition (construct complex real part and imaginary part according to real part and imaginary part) (order to real part and imaginary part))

(Definition (construct complex modulus length angle according to modulus length angle)
    (Sequence pair(* Module length (cosine angle)(* Mode length (sinusoidal amplitude)

The following is a process of polar coordinate representation, that is, the module and argument are obtained directly, but the real part and imaginary part need to be obtained according to the triangular relationship:

(define (magnitude z) (car z))

(define (angle z) (cdr z))

(define (real-part z) 
    (* (magnitude z) (cos (angle z))))

(define (imag-part z)
    (* (magnitude z) (sin (angle z))))

(define (make-from-mag-ang r a)
    (cons r a))

(define (make-from-real-imag x y)
    (cons (sqrt (+ (square x) (square y)))
          (atan y x)))

Try to translate the above process into Chinese:

(Definition (module length complex number) (preceding complex number))

(Definition (argument plural) (latter plural)

(Definition (real part, complex number)
    (* (Module length (complex) (cosine (argument complex))

(Definition (imaginary part and complex number)
    (* (Module length (complex) (sine (argument complex))

(Definition (construct complex modulus length angle according to modulus length angle)
    (Sequence pair module length (argument)

(Definition (construct complex real and imaginary parts according to real and imaginary parts)
    (Sequence pair (square root)(+ (Square real part (square imaginary part))
          (Arctangent imaginary part (real part))

The above two different implementations can ensure that add complex, sub complex, Mul complex and div complex can work normally on their own.

The next step is the focus of our discussion in this section. The bottom layer above realizes two different processes with the same name, and how to coexist harmoniously in a system. I don't know what other readers think. I think the later part of the book enlightens me on the principle of polymorphic underlying implementation. In fact, it's very simple. In C + +, we can easily write functions with polymorphic characteristics, such as function(int a, int b) and function(double a, double b). When calling the two functions later, the compiler can automatically call the one to be called according to the incoming data type. In fact, the most intuitive and concise implementation scheme here (I believe there is a more efficient implementation method for the more underlying language c + +, but now you might as well think about the most intuitive one), that is, you can store the type labels int and double as one item of sequential data. When a call occurs, just compare the item in the sequence that stores the data type label, Then execute the function that should be executed according to the result of the compared data type.

ok, after this, let's look at how this labeling method is used in the book to make two different plural expressions coexist harmoniously in a system:

First of all, we need a process like the one I talked about above to add type labels to the data content and determine what the type labels of the data are:

(define (attach-tag type-tag contents)
    (cons type-tag contents))

(define (type-tag datum)
    (if (pair? datum)
        (car datum)
        (error "Bad tagged datum -- TYPE-TAG" datum)))

(define (contents datum)
    (if (pair? datum)
        (cdr datum)
        (error "Bad tagged datum -- CONTENTS" datum)))

Try to translate the above process into Chinese:

(Definition (binding label type label content)
    (Construction sequence (type label content))

(Definition (type label data content)
    (If (paired? Data content)
          ((data content in the preceding paragraph)
          (Error (wrong labeled data - type label data content))

(Definition (data content)
    (If (paired? Data content)
          (Later data content)
          (Error (wrong tagged data - content)

(Definition (data part with label)
    (If (paired? Tagged data)
          (Last item (data with label)
          (Error (wrong tagged data - data part (tagged data))

(Definition (type label with label data)
    (If (paired? Tagged data)
          (Preceding item (data with label)
          (Error (wrong tagged data - type tag (tagged data))

Then we can write out which representation to judge according to whether the bound label is "rectangular coordinate" or "polar coordinate", whether it is "complex number in rectangular coordinate system" or "complex number in polar coordinate system":

(define (rectangular? z)
    (eq? (type-tag z) 'rectangular))
(define (polar? z)
    (eq? (type-tag z) 'polar))

Try to translate the above process into Chinese:

(Definition (complex number in rectangular coordinate system)
    (For? (type label plural) 'Rectangular coordinates)
(Definition (complex number in polar coordinate system)
    (For? (type label plural) 'Polar coordinates)

With the process of Judging according to the label, we should write the process of labeling. First, based on the previous two types of processes of selecting rectangular coordinates and polar coordinates, as follows:

1. Rectangular coordinate representation

(define (real-part-rectangular z) (car z))

(define (imag-part-rectangular z) (cdr z))

(define (magnitude-rectangular z)
    (sqrt (+ (square (real-part-rectangular z)) 
             (square (imag-part-rectangular z)))))

(define (angle-rectangular z)
    (atan (imag-part z) (real-part z)))

(define (make-from-real-imag-rectangular x y) 
    (attach-tag 'rectangular (cons x y)))

(define (make-from-mag-ang-rectangular r a)
    (attach-tag 'rectangular
                (cons (* r (cos a)) (* r (sin a)))))

Try to translate the above process into Chinese:

(Definition (real part complex number of rectangular coordinate representation) (complex number of the preceding item))
(Definition (real part complex number of rectangular coordinate representation) (complex number of the preceding item))
(Definition (rectangular coordinate representation takes the real part complex number) (the preceding complex number))
(Definition (real part complex number under rectangular coordinate representation) (complex number of the preceding item))
(Definition (real part complex number under rectangular coordinate representation) (preceding complex number))
(Definition (the real part complex number under the rectangular coordinate representation) (the preceding complex number))

(Definition (finding imaginary part complex number by rectangular coordinate representation) (latter complex number))
(Definition (imaginary part complex number of rectangular coordinate representation) (latter complex number))
(Definition (rectangular coordinate representation takes imaginary part complex number) (latter complex number))
(Definition (imaginary part complex number under rectangular coordinate representation) (latter complex number))
(Definition (finding imaginary part complex number under rectangular coordinate representation) (latter complex number))
(Definition (the imaginary part complex number under the rectangular coordinate representation) (the latter complex number))

(Definition (finding module length complex number by rectangular coordinate representation) 
    (Prescription(+ (Square (taking the real part complex number under the rectangular coordinate representation))
              (Square (the imaginary part is taken as the complex number under the rectangular coordinate representation))

(Definition (finding module length complex number under rectangular coordinate representation)
    (Calculation of module length (complex number) by rectangular coordinate representation

(Definition (calculation of argument complex number by rectangular coordinate representation)
    (Arctangent (imaginary part under rectangular coordinate representation) (real part under rectangular coordinate representation))

(Definition (construct the complex real part and imaginary part represented by rectangular coordinate representation according to the real part and imaginary part)
    (Binding label 'Rectangular coordinates (real part and imaginary part of construction order)

(Definition (construct the complex modulus length angle represented by rectangular coordinate representation according to the modulus length angle)
    (Binding label 'Rectangular coordinates (construction sequence pair)(* Module length (cosine angle)(* Mode length (sinusoidal amplitude)

Then there is the modified polar representation:

(define (real-part-polar z)
    (* (magnitude-polar z) (cos (angle-polar z))))
(define (imag-part-polar z)
    (* (magnitude-polar z) (sin (angle-polar z))))
(define (magnitude-polar z) (car z))
(define (angle-polar z) (cdr z))
(define (make-from-real-imag-polar x y)
    (attach-tag 'polar
                (cons (sqrt (+ (square x) (square y)))
                      (atan y x))))
(define (make-from-mag-ang-polar r a)
    (attach-tag 'polar (cons r a)))

Try to translate the above process into Chinese:

(Definition (real part complex number under polar coordinate representation)
    (* (Module length complex under polar coordinate representation (cosine (argument complex under polar coordinate representation))
(Definition (finding imaginary part complex number under polar coordinate representation)
    (* (Module length complex under polar coordinate representation (sinusoidal (argument complex under polar coordinate representation))
(Definition (take the complex number of module length under the polar coordinate representation) (the complex number of the preceding item))
(Definition (taking the argument complex number under the polar coordinate representation) (the latter complex number))
(Definition of the amplitude of the complex module
    (Binding label 'Polar coordinates (sequence versus module length and argument)
(Definition (construct the complex real part and imaginary part represented by polar coordinate representation according to the real part and imaginary part)
    (Binding label 'Rectangular coordinates 
             (Construction sequence (square root)(+ (Square real part (square imaginary part))
                      (Arctangent imaginary part (real part))

With these two modified processes, we can add selection branches to the original real part, imag part, magnet and angle functions, and select the selection function under the corresponding representation to run according to the representation adopted by the incoming complex number:

(define (real-part z)
    (cond ((rectangular? z)
           (real-part-rectangular (contents z)))
          ((polar? z)
           (real-part-polar (contents z)))
          (else (error "Unknown type -- REAL_PART" z))))
(define (imag-part z)
    (cond ((rectangular? z)
           (imag-part-rectangular (contents z)))
          ((polar? z)
           (imag-part-polar (contents z)))
          (else (error "Unknown type -- IMAG_PART" z))))
(define (magnitude z)
    (cond ((rectangular? z)
           (magnitude-rectangular (contents z)))
          ((polar? z)
           (magnitude-polar (contents z)))
          (else (error "Unknown type -- MAGNITUDE" z))))
(define (angle z)
    (cond ((rectangular? z)
           (angle-rectangular (contents z)))
          ((polar? z)
           (angle-polar (contents z)))
          (else (error "Unknown type -- ANGLE" z))))

I have to say that Chinese programming has no advantages over the above contents, but let's write it:

(Definition (real part, complex number)
    (The case conforms to (? - complex number in rectangular coordinate representation)
               (Realistic part under rectangular coordinate representation (data part complex number))
             ((Polar representation? Plural)
               (Realistic part under polar coordinate representation (data part (complex))
             (Otherwise (error "unknown type - real part" complex number))
(Definition (imaginary part and complex number)
    (The situation conforms to ((it is the "complex number" represented by rectangular coordinate representation)
               (Finding imaginary part (data part complex number)) under rectangular coordinate representation
             ((Polar representation? Plural)
               (Finding imaginary part (data part complex number)) under polar coordinate representation
             (Otherwise (error "unknown type - imaginary part" complex number))
(Definition (module length and complex number)
    (The situation is consistent with ((it is a complex number expressed in rectangular coordinate representation)
               (Calculation of module length by rectangular coordinate representation (complex number of data part))
             ((Is it expressed in polar coordinates? Plural)
               (Calculation of module length under polar coordinate representation (complex number of data part))
             (Otherwise (error "unknown type - modulo length" complex)))
(Definition (argument complex)
    (Qingkang coincidence ((it is a complex number expressed in rectangular coordinate representation)
               (Calculation of argument under rectangular coordinate representation (complex number of data part))
             ((Is it expressed in polar coordinates? Plural)
               (Calculation of argument under polar coordinate representation (complex number of data part))
             (Other cases (error "unknown type - argument" plural))

Finally, you need to complete the construction process of the complex number. Now, you can choose the rectangular coordinate representation when you have the real part and imaginary part, and the polar coordinate representation when you have the module length and argument:

(define (make-from-real-imag x y)
    (make-from-real-imag-rectangular x y))
(define (make-from-mag-ang r a)
    (make-from-mag-ang-polar r a))

Try to translate the above process into Chinese:

(Definition (construct the real part and imaginary part of the complex number under the rectangular coordinate representation)
    (According to the real part and imaginary part, the complex real part (imaginary part) under the rectangular coordinate representation is constructed
(Definition (constructing complex real and imaginary parts from real and imaginary parts)
    (According to the real part and imaginary part, the complex real part (imaginary part) under the rectangular coordinate representation is constructed
(Definition (construction of complex modulus length and argument under polar coordinate representation)
    (The complex module length (argument) in polar coordinate representation is constructed according to the real part and imaginary part
(Definition (construct complex modulus length angle from modulus length angle)
    (According to the module length and angle, the complex module length and angle under the polar coordinate representation)

If the above modified process is applied, the previous processes such as complex addition, complex subtraction, complex multiplication and complex division can be used without changing the implementation. For example, add complex is still:

(define (add-complex z1 z2)
    (make-from-real-imag (+ (real-part z1) (real-part z2))
                         (+ (imag-part z1) (imag-part z2))))

Translated into Chinese:

(Definition (plural addition plural a plural b)
    (Constructing complex numbers in rectangular coordinates(+ (Real part plural a) (real part plural b)
                         (+ (Imaginary part complex a) (imaginary part complex B))

In fact, the above integration ideas can be intuitively represented by the picture in the book:

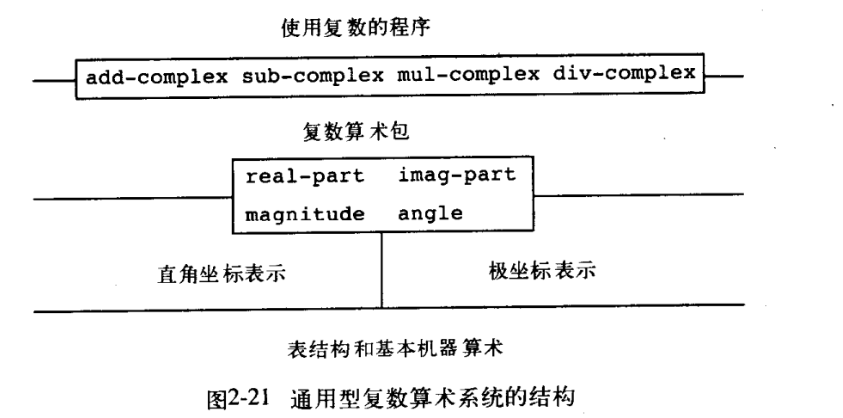
However, there is an obvious problem in the process of transformation, that is, it's too verbose! Whether it's "magnitude rectangular" in English or the kind of "finding module length under rectangular coordinate representation" I wrote, and it's not just a nagging problem. When connecting the two representations into one system, it's necessary to rename each process of the two representations (to ensure that there is no duplicate name), That is, in English, for example, the original "angle" is changed to "angle rectangular" and "angle polar", and the Chinese version I wrote, in order to pursue the fluency of a natural language, even the long names of "calculating the angle in rectangular coordinate system" and "calculating the angle in polar coordinate system" have been dried out. Maybe it's OK that the system has only two layers and two branches. This guy, if the system has three layers and four layers, three types of branches and four types of branches, it's still named like this. Why don't people collapse?

(another problem is that in the above process, there is such a sentence (data part plural) or true literal translation, which is called (content plural). This sentence is really strange to read, although we know that this is because if there is labeled data, such a sentence is required to obtain the real data part that is not a label, But that doesn't change the fact that it's strange to read. Is it possible to improve this question? I don't have an answer yet.)

In fact, I think to understand how to solve the first problem I raised above, we can also talk about what polymorphism is like in C + +, such as:

void option(int a){}
//and
void option(double b){}
//You then declare:
int a;
//and
double b;
//When calling, you write
option(a);
//and
option(b);
//The compiler will automatically call the called function.

You find a very smooth point here is that when you declare int a; After that, write a, and the compiler will know that this a is of int type. As a programmer, it is not necessary and should not show how to add int label to a in this visible program, and when the user (of course, the user here refers to ourselves) declares a, The process of how to obtain the type tag of a (it is still very unprofessional to assume that C + + obtains the type of a variable, similar to obtaining what is an item in a sequence stored in a variable). Of course, there should be such a process logically, but such a process should exist at another level.

Back to the book, let's take a look at the examples in the book, which are how to inject variable related type labels into variables at another level, and how to implement when using a variable or process (of course, in scheme language, there is a feature that variables and processes are the same), You can finish the process corresponding to the type label of this variable or process in advance. (I feel like I wrote a "long and difficult sentence in Chinese"? It's dry. Let's change it a little more like human words later)

In fact, it is the latter two processes, put and get. Put can inject type tags into variables; Get can get the type label of the variable. The formats of the two are as follows:

(put <op> <type> <item>)

(get <op> <type>)

After some consideration, I decided to temporarily name put "injection". From the perspective of code, it injects the process to be executed and a type label into a variable you declare (again, the variable in scheme is equivalent to the process).

And get, perhaps the most direct translation is "get", which is embedded in the pseudo code above, which means "get the corresponding operation under a certain type of label".

Well, try to translate the above two processes into Chinese:

(injection <operation> <Type label> <variable>)

(obtain <operation> <Type label>)

ok, after these two processes, let's take a look at how labels can be written now:

1. Rectangular coordinate representation

(define (install-recatngular-package)

;;internal procedures
(define (real-part z) (car z))
(define (imag-part z) (cdr z))
(define (make-from-real-imag x y) (cons x y))
(define (magnitude z)
    (sqrt (+ (square (real-part z))
             (square (imag-part z))))))
(define (angle z)
    (atan (imag-part z) (real-part z)))
(define (make-from-mag-ang r a)
    (cons (* r (cos a)) (* r (sin a))))

;;interface to the rest of the system
(define (tag x) (attach-tag 'rectangular x))
(put 'real-part '(rectangular) real-part)
(put 'imag-part '(rectangular) imag-part)
(put 'magnitude '(rectangular) magnitude)
(put 'angle '(rectangular) angle)
(put 'make-from-real-imag 'rectangular
     (lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'rectangular
     (lambda (r a) (tag (make-from-mag-ang r a))))
'done)

Try to translate the above process into Chinese:

(Definition (complex rectangular representation related process set)
；；Internal process
(Definition (real part plural) (preceding plural))
(Definition (imaginary part complex number) (subsequent complex number))
(Definition (construct complex real part and imaginary part from real part and imaginary part) (construction order to real part and imaginary part))
(Definition (module length and complex number)
    (Prescription(+ (Square (real part, complex part)
              (Square (imaginary part, complex number))
(Definition (argument complex)
    (Arctangent (imaginary part complex number) (real part complex number))
(Definition (construct complex modulus length angle from modulus length angle)
    (Structural sequence pair(* Module length (cosine angle)(* Mode length (sinusoidal amplitude)

；；Add a "Cartesian coordinate system" label to all internal processes to form an interface to the outside of the system
(Definition (tag element) (binding tag) 'Rectangular coordinate system (element)
(injection 'real part  '(Rectangular coordinate system (real part)
(injection 'imaginary part  '(Cartesian coordinate system (imaginary part)
(injection 'Die length  '(Rectangular coordinate system (mold length)
(injection 'Argument  '(Rectangular coordinate system (argument)
(injection 'Constructing complex numbers from real and imaginary parts 'Rectangular coordinate system
     (For (real part and imaginary part) (label (construct complex real part and imaginary part from real part and imaginary part)))
(injection 'Constructing complex number from module length and argument 'Rectangular coordinate system
     (It is specified that for (module length and angle) (label (construct complex module length and angle from module length and angle)))
'(done)

Excellent coding, the code is enough to explain itself. If I want to explain what the above code is doing again, I can almost say so, "First, the definition of the complex constructor and selection function under the rectangular coordinate representation. This piece of code appeared above, and then add the corresponding operation and type labels to these functions. In this way, when a constructor or selection function is used outside, the 'rectangular coordinate' label and the operation to be performed are in the 'function name' ’(I don't know if you can understand my statement. It's like an int shaped A. when you use a, 'Int' seems to be in it). " Such an explanation seems to be really explained with heart, but in my case, it's like I just read the code once. The above code is neatly divided into two parts. I think if you want to understand it, you can scan it faster than watching me explain such a big sentence.

2. Polar coordinate representation

(define (install-polar-package)
;;internal procedures
(define (magnitude z) (car z))
(define (angle z) (cdr z))
(define (real-part z) 
    (* (magnitude z) (cos (angle z))))
(define (imag-part z)
    (* (magnitude z) (sin (angle z))))
(define (make-from-mag-ang r a)
    (cons r a))
(define (make-from-real-imag x y)
    (cons (sqrt (+ (square x) (square y)))
          (atan y x)))
          
;;interface to the rest of the system
(define (tag x) (attach-tag 'polar x))
(put 'real-part '(polar) real-part)
(put 'imag-part '(polar) imag-part)
(put 'magnitude '(polar) magnitude)
(put 'angle '(polar) angle)
(put 'make-from-real-imag 'polar
     (lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'polar
     (lambda (r a) (tag (make-from-mag-ang r a))))
'done)

(Definition (complex polar representation related process set)
；；Internal process
(Definition (module length complex number) (preceding complex number))
(Definition (argument plural) (latter plural)
(Definition (real part, complex number)
    (* (Module length (complex) (cosine (argument complex))
(Definition (imaginary part and complex number)
    (* (Module length (complex) (sine (argument complex))
(Definition (construct complex modulus length angle from modulus length angle)
    (Structural order versus module length (argument)
(Definition (constructing complex real and imaginary parts from real and imaginary parts)
    (Structural sequence pair (square root)(+ (Square real part (square imaginary part))
             (Arctangent imaginary part (real part))

；；Label all internal processes with "polar coordinate system" to form an interface to the outside of the system
(injection 'real part  '(Polar coordinate system (real part)
(injection 'imaginary part  '(Polar coordinate system (imaginary part)
(injection 'Die length  '(Polar coordinate system (mold length)
(injection 'Argument  '(Polar coordinate system (argument)
(injection 'Constructing complex numbers from real and imaginary parts 'Polar coordinate system
    (Specifies the binding label for (real part and imaginary part) 'Polar coordinate system (complex real part and imaginary part are constructed from real part and imaginary part)
(injection 'Constructing complex number from module length and argument 'Polar coordinate system
    (Specifies the binding label for (real part and imaginary part) 'Polar coordinate system (complex modulus length angle is constructed from modulus length angle))
'(done)

In this way, we can reliably follow the relevant process of writing two complex representation methods when programming according to desire at the beginning, put the labels of "rectangular coordinates" and "polar coordinates" in another place below, and use the unified "injection", that is, the method of putting these things into. In this way, you don't have to worry about the problem of duplicate names. You don't have to lengthen the thief who changed the original good process name as the system gets bigger. It's great to write code.

Now that we know how to add labels, we should learn how to take labels and perform the corresponding operation process. In the book, a function called apply generic is used to do this:

(define (apply-generic op . args)
    (let ((type-tags (map type-tag args)))
      (let ((proc (get op type-tags)))
        (if proc
            (apply proc (map contents args))
            (error
              "No method for these types -- APPLY-GENERIC"
              (list op type-tags))))))

Try to translate the above process into Chinese:

(Definition (general application operation) · Parameters); There may be more than one parameter here. This sentence should read "perform a certain operation on all parameters"
    ((type label set (each type label parameter)); It can be read as "type label of each parameter"
      (Command ((the operation to be performed (get the operation type label set)); Here, you can read "get operation under type tag set"
        (If the operation to be performed 
             (The operation performed by the application (each data part parameter)); This sentence can be read as "apply the operation to the data part of each parameter"
             (error
                "There is no corresponding operation under the required type label - general application "
                (Sequence operation (all type labels))

Using apply generic, various general-purpose selection functions can be defined as follows:

(define (real-part z) (apply-generic 'real-part z))
(define (imag-part z) (apply-generic 'imag-part z))
(define (magnitude z) (apply-generic 'magnitude z))
(define (angle z) (apply-generic 'angle z))

Try to translate the above process into Chinese:

(Definition (real part and complex number) (general application) 'Real part (complex)
(Definition (imaginary part and complex number) (general application) 'Imaginary part (complex)
(Definition (module length and complex number) (general application) 'Module length (complex)
(Definition (argument complex) (general application) 'Argument (complex)

In fact, I'm not satisfied with the Chinese version now. I'm not satisfied with it now

Now, our constructor can be written like this, and finally it can be written like this:

(Definition (construct the real part and imaginary part of the complex number in the rectangular coordinate system)
    ((obtain 'Constructing complex numbers from real and imaginary parts 'Cartesian coordinate system (real part and imaginary part)
；This line here is to first obtain the "complex number constructed from real part and imaginary part" under the "rectangular coordinate system", and then execute this acquisition process for the two parameters of "real part" and "imaginary part"
(Definition (construction of complex modulus length and argument in polar coordinate system)
    ((obtain 'Constructing complex number from module length and argument 'Polar coordinate system) module length (argument)
；Similarly, get it first"Polar coordinate system"After obtaining the "complex number constructed from module length and angle", you will find that the bracket in front can be removed, and the obtained process name can be used to execute the following two parameters of "module length" and "angle".

Don't write the English version first when you are excited. English version:

(define (make-from-real-imag x y)
    ((get 'make-from-real-imag 'rectangular) x y))
(define (make-from-mag-ang r a)
    ((get 'make-from-mag-ang 'polar) r a))

Exercise 2.73 in the previous "literal translation of scheme language into Chinese (17)", a program describing the execution of symbolic derivation is written:

(define (deriv exp var)
    (cond ((number? exp) 0)
          ((variable? exp) (if (same-variable? exp var) 1 0))
          ((sum? exp)
           (make-sum (deriv (addend exp) var)
                     (deriv (augend exp) var)))
          ((product? exp)
           (make-sum
             (make-product (multiplier exp)
                           (deriv (multiplicand exp) var))
             (make-product (deriv (multiplier exp) var)
                           (multiplicand exp))))
<More rules can be added here>
          (else (error "unknown expression type -- DERIV" exp))))

Try to translate the above process into Chinese:

(Definition (derivative expression variable)
    (The situation conforms to ((is numeric? Expression) 0)
               ((Is it a variable? Expression) (if (is the same variable? Expression variable) 1 0))
             ((Is it harmony? (expression)
               (Construction sum formula (derivative (addend expression) variable)
                        (Derivative (addend expression) (variable)
             ((Is it multiplication? (expression)
               (Construction and formula 
                 (Construct multiplier (multiplicand expression)
                          (Derivative (multiplier expression) (variable)
                 (Construct a multiplier (derivative (multiplicand expression) variable)
                          (Multiplier expression)
              <More rules can be added here>
             (Other cases (wrong "unknown expression type - derivative" expression))

Then we notice that the derivation process can be understood as a process of retrieving the corresponding process according to the expression symbols. With this idea, we can write the following code:

(define (deriv exp var)
    (cond ((number? exp) 0)
          ((variable? exp) (if (same-variable? exp var) 1 0))
          (else ((get 'deriv (operator exp)) (operands exp) var))))
(define (operator exp) (car exp))
(define (operands exp) (cdr exp))

Try to translate the above process into Chinese:

(Definition (derivative expression variable)
    (The situation conforms to ((is numeric? Expression) 0)
             ((Is itself a variable? Expression) (if (is the same variable? Expression variable) 1 0))
             (Other information (obtained) 'Derivative (operation sign expression) (operand expression) (variable))
(Definition (operation symbol expression) (previous expression))
(Definition (operand expression) (subsequent expression))

a) Please explain what the above does. Why can't we put the near predicate number? And same variable? Also included in data-oriented dispatch?
b) Please write the derivation process for sum and product and install them into the table so that the above program can use the auxiliary code required.
c) Please select some derivation rules you want to include, such as deriving powers (exercise 2.56), and install them into this data-oriented system.
d) In this simple algebraic operator, the type of expression is the algebraic operator from which they are constructed. Suppose we want to index in the opposite way so that the lines of code that complete the dispatch in the deriv are as follows:
((get (operator exp) 'deriv) (operands exp) var)
What corresponding changes need to be made in the derivation system?

Solution:
a) The above new process is a program that selects the corresponding derivation process according to the expression operator, because for number? And same variable? The expression to be judged has no operation symbols, so we can't write them in this way.
b) In fact, I don't know the original meaning of this question. Should I come up with the writing method of "installing into the form" by myself? I checked on the Internet. Others said that to complete this problem, we should first move a program on page 186 in the book that seems to build and insert statements into the table to realize the definition of put and get first. I decided to do the same first.

define-put-get.ss:

;Page 186 is right put and get Definition of
(define (make-table)
  (let ((local-table (list '*table*)))
    (define (lookup key-1 key-2)
      (let ((subtable (assoc key-1 (cdr local-table))))
        (if subtable
            (let ((record (assoc key-2 (cdr subtable))))
              (if record
                  (cdr record)
                  false))
            false)))
    (define (insert! key-1 key-2 value)
      (let ((subtable (assoc key-1 (cdr local-table))))
        (if subtable
            (let ((record (assoc key-2 (cdr subtable))))
              (if record
                  (set-cdr! record value)
                  (set-cdr! subtable
                            (cons (cons key-2 value)
                                  (cdr subtable)))))
            (set-cdr! local-table
                      (cons (list key-1
                                  (cons key-2 value))
                            (cdr local-table)))))
      'ok)
    (define (dispatch m)
      (cond ((eq? m 'lookup-proc) lookup)
            ((eq? m 'insert-proc!) insert!)
            (else (error "Unknown operation -- TABLE" m))))
    dispatch))

(define operation-table (make-table))
(define get (operation-table 'lookup-proc))
(define put (operation-table 'insert-proc!))

basic-judgment.ss:

(define (variable? x) (symbol? x))

(define (same-variable? x v) (eq? x v))

(define (=number? x num)
  (and (number? x) (= x num)))

73-deriv.ss:

(load "base-judgment.ss")
(define (deriv exp var)
    (cond ((number? exp) 0)
          ((variable? exp) (if (same-variable? exp var) 1 0))
          (else ((get 'deriv (operator exp)) (operands exp) var))))
(define (operator exp) (car exp))
(define (operands exp) (cdr exp))

install-sum-package.ss

(define (install-sum-package)
  (define (make-sum a1 a2)
    (cond ((=number? a1 0) a2)
          ((=number? a2 0) a1)
          ((and (number? a1) (number? a2)) (+ a1 a2))
          (else (list '+ a1 a2))))
  (define (addend operands) (car operands))
  (define (augend operands) (cadr operands))
  (define (deriv-sum operands var)
    (make-sum (deriv (addend operands) var)
              (deriv (augend operands) var)))

  (put 'make '+ make-sum)
  (put 'deriv '+ deriv-sum)
  (display "Install sum package done\n"))

(define (make-sum a1 a2)
  ((get 'make '+) a1 a2))

install-product-package.ss

(define (install-product-package)
  (define (make-product m1 m2)
    (cond ((or (=number? m1 0) (=number? m2 0)) 0)
          ((=number? m1 1) m2)
          ((=number? m2 1) m1)
          (else (list '* m1 m2))))
  (define (multiplier operands) (car operands))
  (define (multiplicand operands) (cadr operands))
  (define (deriv-product operands var)
    (make-sum
     (make-product (multiplier operands)
                   (deriv (multiplicand operands) var))
     (make-product (deriv (multiplier operands) var)
                   (multiplicand operands))))

  (put 'make '* make-product)
  (put 'deriv '* deriv-product)
  (display "Install product package done\n"))

(define (make-product m1 m2)
  ((get 'make '*) m1 m2))

test.ss:

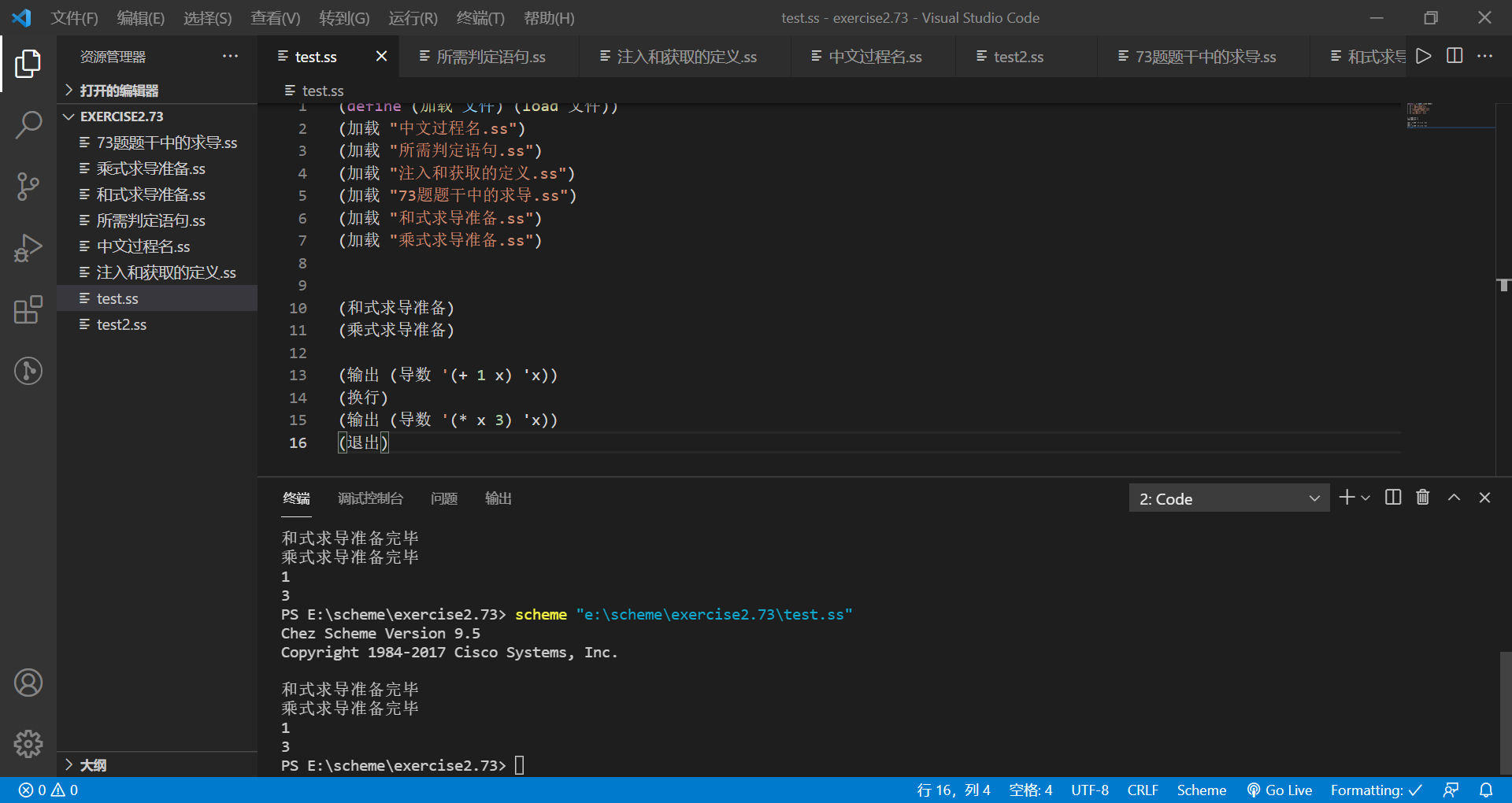
(load "install-sum-package.ss")
(load "install-product-package.ss")
(load "73-deriv.ss")
(load "define-put-get.ss")

(install-sum-package)
(install-product-package)

(display (deriv '(+ x 3) 'x))
(newline)
(display (deriv '(* x 3) 'x))
(exit)

Then there is the version named in Chinese:

Chinese process name ss:

(define (It's a digital element) (number? element))
(define (Is a numeric element) (number? element))
(define (If it is a digital element) (number? element))
(define (If it is a digital element) (number? element))
(define (Is it a number) (number? element))
(define (Is it a number) (number? element))

;(define (Conditions a and B) (and Condition a condition B))
;(define (Condition a or condition B) (or Condition a condition B))
;The actual measurement of "and" or "cannot be done hastily, and some strange phenomena will appear bug，In the future, write it after you really understand the principle of and or operation of infinite numbers


(define (Antecedent sequence pair) (car Sequence pair))
(define (Preceding sequence pair) (car Sequence pair))
(define (Subsequent sequence pair) (cdr Sequence pair))
(define (Subsequent sequence pairs) (cdr Sequence pair))

(define (First term sequence) (car sequence))
(define (Second term sequence) (cadr sequence))
(define (Third term sequence) (caddr sequence))
(define (Fourth term sequence) (cadddr sequence))

(define (Output content) (display content))

(define (Line feed) (newline))

(define (sign out) (exit))

Definition of injection and acquisition ss (because I haven't learned it yet, I won't change it first):

;Page 186 is right put and get Definition of
(define (make-table)
  (let ((local-table (list '*table*)))
    (define (lookup key-1 key-2)
      (let ((subtable (assoc key-1 (cdr local-table))))
        (if subtable
            (let ((record (assoc key-2 (cdr subtable))))
              (if record
                  (cdr record)
                  false))
            false)))
    (define (insert! key-1 key-2 value)
      (let ((subtable (assoc key-1 (cdr local-table))))
        (if subtable
            (let ((record (assoc key-2 (cdr subtable))))
              (if record
                  (set-cdr! record value)
                  (set-cdr! subtable
                            (cons (cons key-2 value)
                                  (cdr subtable)))))
            (set-cdr! local-table
                      (cons (list key-1
                                  (cons key-2 value))
                            (cdr local-table)))))
      'ok)
    (define (dispatch m)
      (cond ((eq? m 'lookup-proc) lookup)
            ((eq? m 'insert-proc!) insert!)
            (else (error "Unknown operation -- TABLE" m))))
    dispatch))

(define operation-table (make-table))

(define get (operation-table 'lookup-proc))
(define obtain (operation-table 'lookup-proc))

(define put (operation-table 'insert-proc!))
(define injection (operation-table 'insert-proc!))

Required decision statement ss:

(define (Load file) (load file))
(load "Chinese process name.ss")

(define (variable? x) (symbol? x))
(define (Is a variable element) (variable? element))
(define (Variable element) (variable? element))
(define (If it is a variable element) (variable? element))
(define (If variable element) (variable? element))
(define (Is it a variable) (variable? element))
(define (Is it a variable) (variable? element))

(define (same-variable? x v) (eq? x v))
(define (Is the same variable) (same-variable? A and B))
(define (For the same variable) (same-variable? A and B))
(define (If it is the same variable) (same-variable? A and B))
(define (If it is the same variable) (same-variable? A and B))
(define (Is it the same variable) (same-variable? A and B))
(define (For the same variable) (same-variable? A and B))


(define (=number? x num)
  (and (number? x) (= x num)))
(define (Equal to the given value)
    (and (Is a numeric element) (= Given value of element)))
(define (Equal to the given value) 
    (and (Is a numeric element) (= Given value of element)))
(define (If equal to the given value) 
    (and (Is a numeric element) (= Given value of element)))
(define (If equal to the given value) 
    (and (Is a numeric element) (= Given value of element)))

Derivation in the stem of question 73 ss:

(define (Load file) (load file))
(load "Chinese process name.ss")
(load "Required decision statement.ss")

(define (Derivative expression argument)
  (cond ((If it is a numeric expression) 0)
        ((If it is a variable expression) (if (Is an argument to the same variable expression) 1 0))
        (else ((obtain 'Derivation (Operator expression)) (Operand expression)
                                           independent variable))))

(define (Operator expression) (Preceding item expression))
(define (Operation symbol expression) (Operator expression))

(define (Operand expression) (Subsequent item expression))

Preparation for derivation of sum ss:

(define (Load file) (load file))
(load "Chinese process name.ss")

(define (Sum derivative preparation)
  (define (Construction sum addend addend)
    (cond ((If equal to the given value, the addend is 0) Addend)
          ((If equal to the given value plus 0) augend)
          ((And (If it's a number addend) (If it's a number plus)) (+ Addend))
          (else (list '+ Addend))))
  (define (Addend operand) (First operand))
  (define (Addend operand) (Second operand))
  (define (Sum derivative operand argument)
    (Construction and formula (derivatives (Addend operand) independent variable)
             (derivatives (Addend operand) independent variable)))
    
  (injection 'structure '+ Construction and formula)
  (injection 'Derivation '+ Sum derivative)
  (output "The sum derivative is ready\n"))

(define (Construction sum addend addend)
  ((obtain 'structure '+) Addend))

Preparation for multiplicative derivation ss:

(define (Load file) (load file))
(load "Chinese process name.ss")

(define (Multiplicative derivation preparation)
  (define (Construct multiplicative multiplicand multiplier)
    (cond ((or (If equal to the given value, the multiplier is 0) (If equal to the given value multiplier 0)) 0)     ;I don't know why, if "or" is used here in Chinese, there will be an error?!
          ((If equal to the given value, the multiplier is 1) multiplier)
          ((If equal to the given value multiplier 1) Multiplicand)
          (else (list '* Multiplicand multiplier))))
  (define (Multiplicand operand) (First operand))
  (define (Multiplier operand) (Second operand))
  (define (Multiplicative derivation operand argument)
    (Construction and formula
     (Constructive multiplication (Multiplicand operand)
              (derivatives (Multiplier operand) independent variable))
     (Constructive multiplication (derivatives (Multiplicand operand) independent variable)
              (Multiplier operation))))

  (injection 'structure '* Constructive multiplication)
  (injection 'Derivation '* Multiplicative derivation)
  (output "The multiplicative derivative is ready\n"))

(define (Construct multiplicative multiplicand multiplier)
  ((obtain 'structure '*) Multiplicand multiplier))

test.ss:

(define (Load file) (load file))
(load "Chinese process name.ss")
(load "Required decision statement.ss")
(load "Definition of injection and acquisition.ss")
(load "73 Derivation in problem stem.ss")
(load "Sum derivative preparation.ss")
(load "Multiplicative derivation preparation.ss")

(Sum derivative preparation)
(Multiplicative derivation preparation)

(output (derivatives '(+ 1 x) 'x))
(Line feed)
(output (derivatives '(* x 3) 'x))
(sign out)

c) Try putting the power in:
English named version:
install-exponentiation-package.ss:

(define (** base exponent)
  (if (= exponent 0)
      1
      (* base (** base (- exponent 1)))))

(define (install-exponentiation-package)
  (define (make-exponentiation b e)
    (cond ((=number? e 0) 1)
          ((=number? e 1) b)
          ((and (number? b) (number? e)) (** b e))
          (else (list '** b e))))
  (define (base operands) (car operands))
  (define (exponent operands) (cadr operands))
  (define (deriv-exponentiation operands var)
    (make-product
     (make-product
      (exponent operands)
      (make-exponentiation (base operands) (- (exponent operands) 1)))
     (deriv (base operands) var)))

  (put 'make '** make-exponentiation)
  (put 'deriv '** deriv-exponentiation)
  (display "Install exponentiation package done\n"))

(define (make-exponentiation b e)
  ((get 'make '**) b e))

Chinese named version:

Exponential derivation preparation ss:

(define (Load file) (load file))
(load "Chinese process name.ss")

;Use“**"Represents a power sign
(define (** Base index)
  (if (= Index 0)
      1
      (* base number (** base number (- Index 1)))))

(define (Exponential derivation preparation)
  (define (Construct exponential base index)
    (cond ((If equal to the given value, the exponent is 0) 1)
          ((If equal to the given value index 1) base number)
          ((and (If it is a base number) (If it's a digital index)) (** Base index))
          (else (list '** Base index))))
  (define (Base operand) (First operand))
  (define (Exponential operand) (Second operand))
  (define (Exponential derivation operand argument)
    (Constructive multiplication
     (Constructive multiplication
      (Exponential operand)
      (Construction index (Base operand) (- (Exponential operand) 1)))
     (derivatives (Base operand) independent variable)))

  (injection 'structure '** Construction index)
  (injection 'Derivation '** Exponential derivation)
  (output "Exponential derivation ready\n"))

(define (Construct exponential base index)
  ((obtain 'structure '**) Base index))

test.ss:

(define (Load file) (load file))
(load "Chinese process name.ss")
(load "Required decision statement.ss")
(load "Definition of injection and acquisition.ss")
(load "73 Derivation in problem stem.ss")
(load "Sum derivative preparation.ss")
(load "Multiplicative derivation preparation.ss")
(load "Exponential derivation preparation.ss")

(Sum derivative preparation)
(Multiplicative derivation preparation)
(Exponential derivation preparation)

(output (derivatives '(+ 1 x) 'x))
(Line feed)
(output (derivatives '(* x 3) 'x))
(Line feed)
(output (derivatives '(** x 3) 'x))
(Line feed)
(output (derivatives '(** (* x 3) 3) 'x))
(sign out)

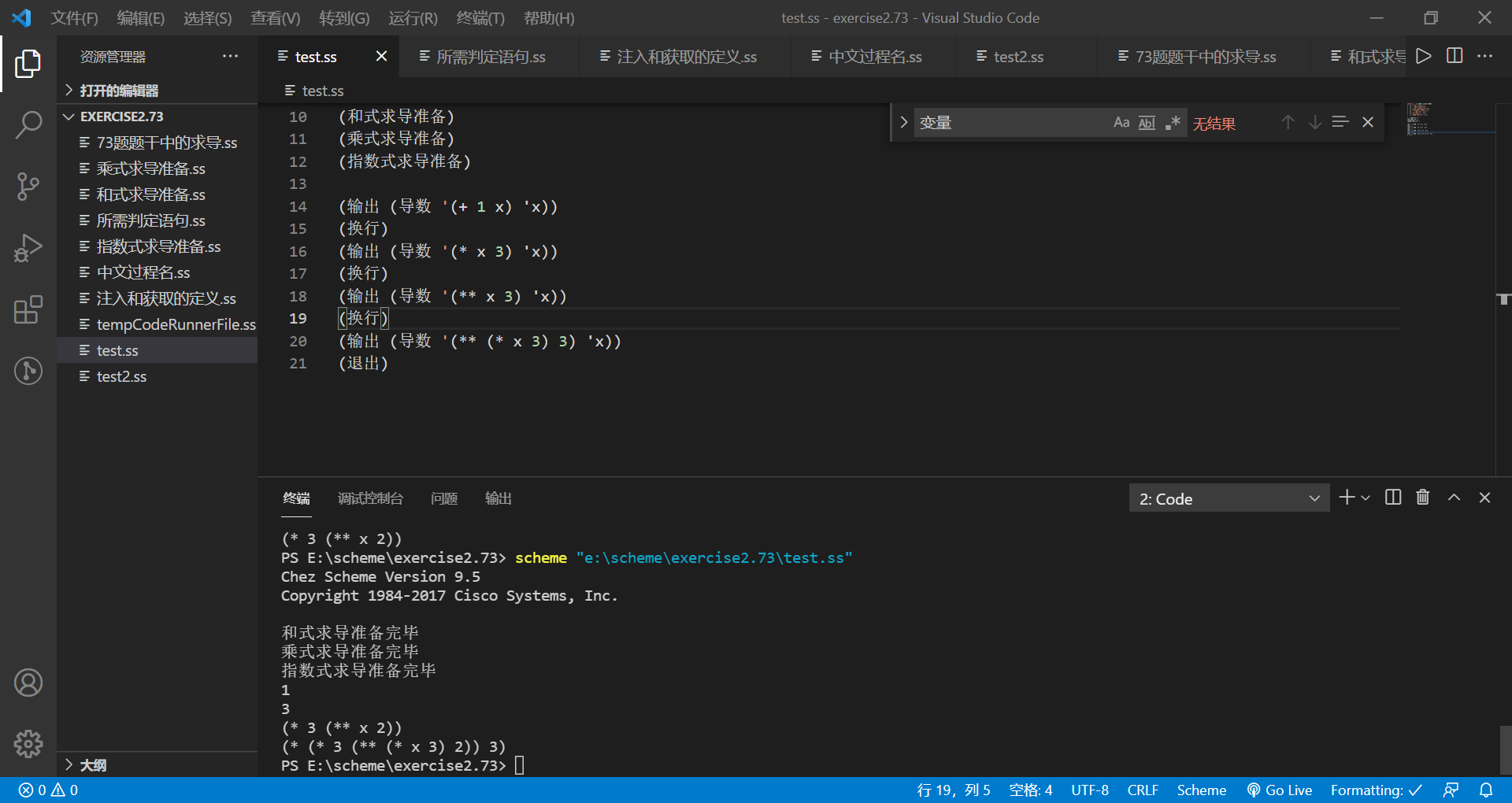
d) For this question, just change the order of the first two parameters in put.

reference:
[1] [US] Julie Sussman Construction and interpretation of computer programs [M] Translated and annotated by Qiu Zongyan Beijing: China Machine Press, 1996
[2] Learn SICP Chapter 2
[3] SICP problem set, exercise 2.73