preface
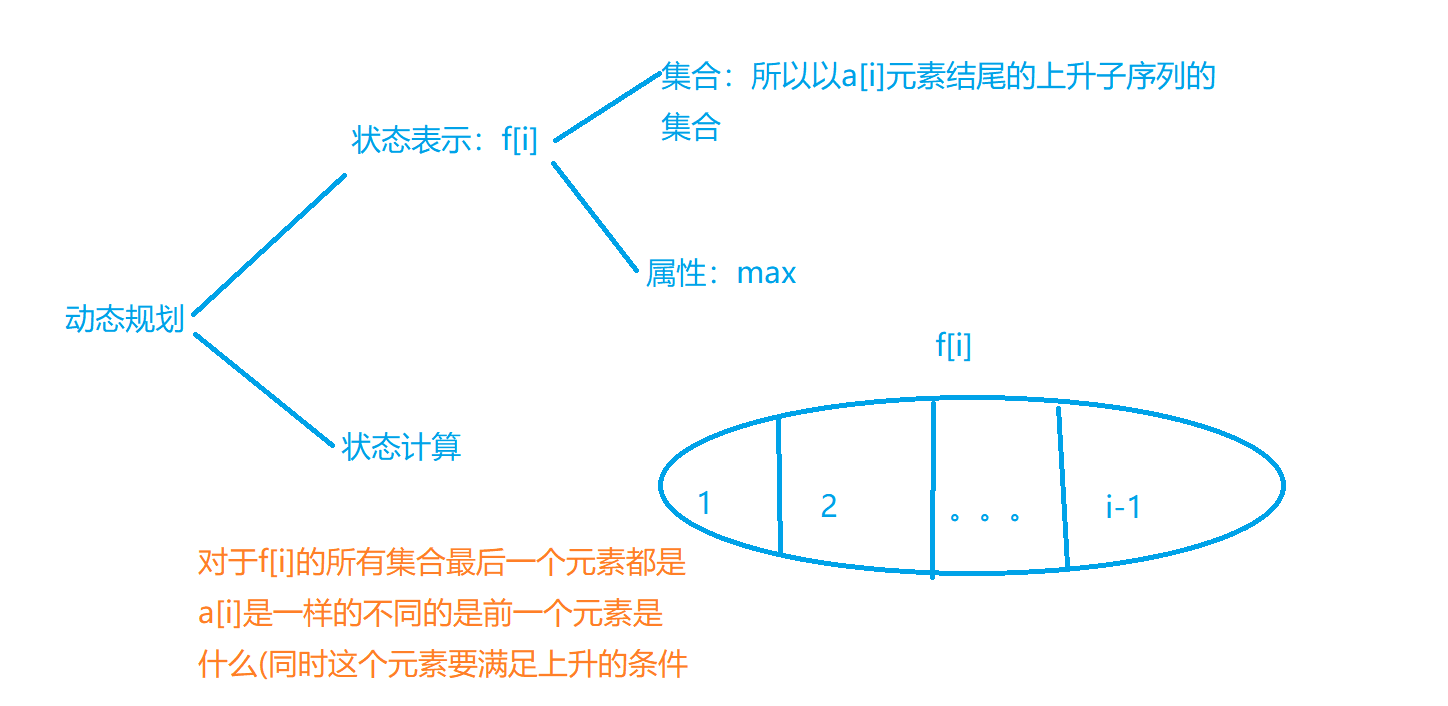
Let's first analyze the original LIS problem with Yan dp analysis
Strange thief Kidd's glider wing
We can start at any point, and there are two directions: left and right. We have to make the most of the buildings we pass
Solution idea: let's take a look at the board problem of the longest body sequence when we start from any point and only go to the right. For the case of going to the left, we only need the longest ascending sub sequence in the opposite direction, and then take a maximum value between the two.
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110 ;
int n ;
int h[N] , f[N];
int main(){
int T;
cin>>T;
while(T--){
cin>>n;
for(int i = 1 ; i <= n ; ++i)cin>>h[i];
int res = 0;
memset(f , 0 , sizeof f);
for(int i = 2 ; i <= n ; ++i)
{
for(int j = 1 ; j < i ; ++j)
if(h[j] < h[i])
f[i] = max(f[i] ,f[j] + 1);
res = max(res , f[i]);
}
memset(f , 0 , sizeof f);
reverse(h+1,h+1+n);
for(int i = 2 ; i <= n ; ++i)
{
for(int j = 1 ; j < i ; ++j)
if(h[j] < h[i])
f[i] = max(f[i] ,f[j] + 1);
res = max(res , f[i]);
}
cout<<res + 1<<endl;
}
return 0;
}
Mountaineering
Analysis Title:

Problem solving ideas:
For this topic, we can also browse scenic spots when we are descending, so we can define another dp formula:
d
[
i
]
d[i]
d[i] represents the longest descending subsequence starting with I. Because for a point I, I can go up or down. comprehensive
f
[
i
]
f[i]
f[i] represents the longest ascending subsequence ending with I, and the result is the maximum of two plus one
code:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010 ;
int n ;
int h[N] ,f[N] ,d[N];
int main(){
cin>>n;
for(int i = 1 ; i <= n ; ++i)cin>>h[i];
for(int i = 2 ; i <= n ; ++i)
for(int j = 1 ; j < i ; ++j)
if(h[i] > h[j])f[i] = max(f[i] ,f[j] + 1);
for(int i = n - 1 ; i >= 1 ; --i)
for(int j = n ; j > i ; --j)
if(h[i] > h[j])d[i] = max(d[i] ,d[j] + 1);
int res = 0;
for(int i = 1 ; i <= n ; ++i)res = max(res ,f[i] + d[i]);
cout<<res+1<<endl;
return 0;
}
Chorus formation
Main idea of the title:
After selecting K people, we make the remaining n-k people, who are satisfied that their height increases from left to right and then decreases. Select k individuals, and K should be as small as possible
Problem solving ideas:
If K is as small as possible, we can change to n-k as large as possible, and the height of these people meets the conditions of drawing
Is this the same as the above topic, so we can directly apply the above and change it when outputting
code:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010 ;
int n ;
int h[N] ,f[N] ,d[N];
int main(){
cin>>n;
for(int i = 1 ; i <= n ; ++i)cin>>h[i];
for(int i = 2 ; i <= n ; ++i)
for(int j = 1 ; j < i ; ++j)
if(h[i] > h[j])f[i] = max(f[i] ,f[j] + 1);
for(int i = n - 1 ; i >= 1 ; --i)
for(int j = n ; j > i ; --j)
if(h[i] > h[j])d[i] = max(d[i] ,d[j] + 1);
int res = 0;
for(int i = 1 ; i <= n ; ++i)res = max(res ,f[i] + d[i]);
cout<<n - res - 1<<endl;
return 0;
}
Sister city
Problem solving ideas:
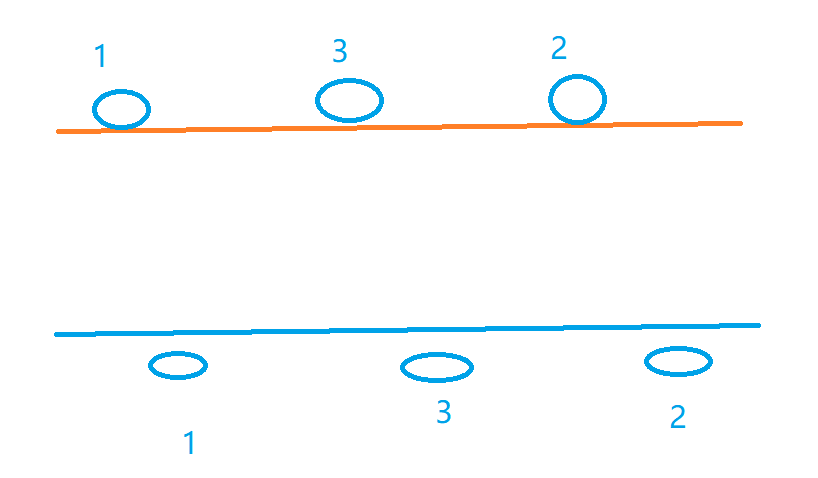
First of all, we understand the premise that the route does not intersect is that the coordinates of the cities on the right in the South and North are larger than those on the left. Therefore, I still apply the template, which is only two-dimensional, so the judgment of the size is different, and then I found that I was wrong. After thinking for a while, recall the second question. The longest upper body sequence is a sub sequence on the original sequence, and the number is required to be incremented. However, if we read it in the original order, we should not be a sub sequence. So we need to sort the original sequence first and then.
As shown in the following figure, if the original reading order is like this, then we should use 2 directly, but it is actually 3
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 5010;
int n ;
struct City{
int x, y;
bool operator < (const City & w)const{
if(x == w.x)return y < w.y;
else return x < w.x;
}
}c[N];
int f[N];
bool check(City a , City b){
if(b.x > a.x && b.y > a.y )return true;
return false;
}
int main(){
cin>>n;
for(int i = 1 ; i <= n ; ++i){
int x , y ;
cin>>x>>y;
c[i] = {x,y};
}
sort(c+1,c+1+n);
for(int i = 2 ; i <= n ; ++i)
for(int j = 1 ; j < i ; ++j)
if(check(c[j],c[i]))f[i] = max(f[i],f[j] + 1);
int res = 0;
for(int i = 2 ; i <= n ; ++i) res = max(res ,f[i] + 1);
cout<<res<<endl;
return 0;
}
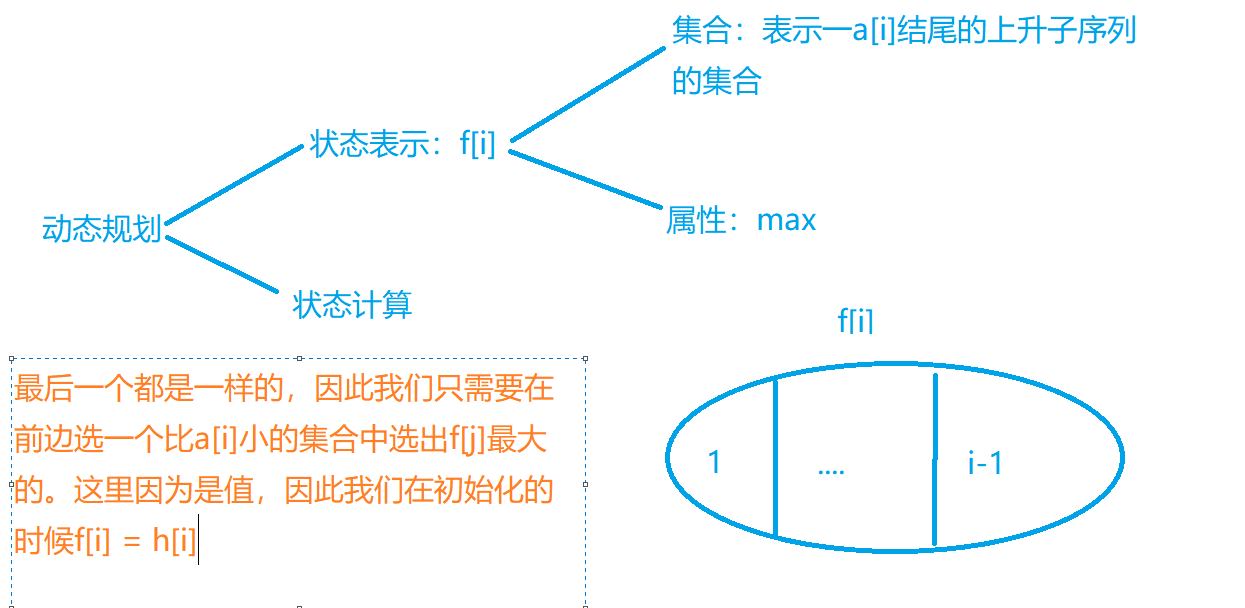
Maximum ascending subsequence sum
Problem solving ideas:
code:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n ;
int h[N] ,f[N];
int main(){
cin>>n;
for(int i = 1 ; i <= n ; ++i)cin>>h[i] ,f[i] = h[i] ;
for(int i = 2 ; i <= n ; ++i)
for(int j = 1 ; j < i ; ++j)
if(h[j] < h[i])f[i] = max(f[i] ,f[j] + h[i]);
int res = 0;
for(int i = 1; i <= n ; ++i) res = max(res ,f[i]);
cout<<res<<endl;
return 0;
}
Interceptor missile (dp + greed)
The difficulty of this problem is the second question. We use greed to solve it

This greedy thinking as like as two peas in the sequence of optimal ascending subsequence is the same.
Optimization of longest ascending subsequence
We will find that the elements in the g array that stores the last element of each sequence are monotonically increasing, so we can use dichotomy to find it when looking for it.
Because of the small amount of data here, you don't need two points
code:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n ;
int h[N] ,f[N] ,g[N];
int main(){
while(cin>>h[++n]){f[n] = 1;}
n--;
for(int i = 2 ; i <= n ; ++i)
for(int j = 1 ; j < i ; ++j)
if(h[j] >= h[i])f[i] = max(f[i] ,f[j] + 1);
int res = 0 , cnt = 0 ;
for(int i = 1 ; i <= n ; ++i) {
int k = 0;
while(k < cnt && g[k] < h[i])k++;
g[k] = h[i];
if(k >= cnt)cnt++;
res = max(res ,f[i]);
}
cout<<res<<endl<<cnt<<endl;
return 0;
}