1. Longest common subsequence (discontinuous)

It refers to the subsequence formed by randomly removing some characters from a given sequence. (random means that some can be removed discontinuously or none can be removed)

For example, for the following two sequences
a: abcbdb
b: acbbabdbb
Their longest common subsequence: acbdb, length 5.

It is solved by dynamic programming, and f [I, J] is defined as( a 0 , a 1 , . . . a i − 1 a_0,a_1,...a_{i-1} a0​,a1​,... ai − 1) and( b 0 , b 1 , . . . b j − 1 b_0,b_1,...b_{j-1} b0​,b1​,... The longest common subsequence length of bj − 1).

Therefore, according to the definition, the search process is divided into the following three cases:

1. When i=0 or j=0, f [I, J] = 0, corresponding to the boundary condition.
2. When a [I-1] = B [J-1], further solve a sub problem and continue to find( a 0 , a 1 , . . . a i − 2 a_0,a_1,...a_{i-2} a0​,a1​,... ai − 2) and( b 0 , b 1 , . . . b j − 2 b_0,b_1,...b_{j-2} b0​,b1​,... The longest common subsequence length of bj − 2). State transition equation f [I, J] = f [I-1, J-1] + 1.
3. When a [I-1] ≠ B [J-1], it is divided into two subproblems, which need to be found out separately( a 0 , a 1 , . . . a i − 1 a_0,a_1,...a_{i-1} a0​,a1​,... ai − 1) and( b 0 , b 1 , . . . b j − 2 b_0,b_1,...b_{j-2} b0​,b1​,... bj − 2) and( a 0 , a 1 , . . . a i − 2 a_0,a_1,...a_{i-2} a0​,a1​,... ai − 2) and( b 0 , b 1 , . . . b j − 1 b_0,b_1,...b_{j-1} b0​,b1​,... bj − 1), and take the maximum of the two. Corresponding state transition equation f [I, J] = max (f [I, J-1], f [I-1, J]).

public class LCS {
	char[] a; 						// Storage sequence a
	char[] b; 						// Storage sequence b
	int[][] dp;

	public LCS(String str1, String str2) {
		a = str1.toCharArray();
		b = str2.toCharArray();
		dp = new int[a.length + 1][b.length + 1];
	}

	// Get maximum length
	public int getLenth() {
		for (int i = 1; i <= a.length; i++) {
			for (int j = 1; j <= b.length; j++) {
				if (a[i - 1] == b[j - 1]) {
					dp[i][j] = dp[i - 1][j - 1] + 1;
				} else {
					dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
				}
			}
		}
		return dp[a.length][b.length];
	}

	// Finding subsequences according to dp array is actually the process of reverse restoring the length above
	public StringBuilder getSubSequence() {
		int i = a.length;
		int j = b.length;
		int len = dp[i][j];

		StringBuilder subs = new StringBuilder("");
		while (len > 0) {
			if (dp[i][j] == dp[i - 1][j]) {
				i--;
			} else if (dp[i][j] == dp[i][j - 1]) {
				j--;
			} else {
				// If the above two conditions are not satisfied, there must be dp[i][j]=dp[i-1][j-1]+1, corresponding to a[i-1]=b[j-1]
				subs.append(a[i - 1]);
				i--;
				j--;
				len--;
			}
		}
		return subs.reverse();
	}

	public static void main(String[] args) {
		String str1 = "abcbdb";
		String str2 = "acbbabdbb";
		LCS ls = new LCS(str1, str2);
		System.out.println("Length:" + ls.getLenth());
		System.out.println("Longest common subsequence:" + ls.getSubSequence());
	}
}

dp array in solving process

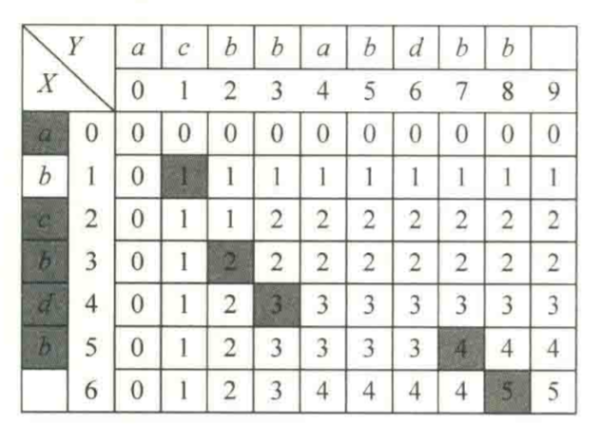
Because two layers of for loops are created and a two-dimensional array is created in the process of solving, the time and space complexity of solving two sequences with lengths of M and N are O ( m n ) Ο(mn) O(mn).

2. Longest common subsequence (continuous)

The longest common continuous subsequence of the above two sequences is:
a: abcbdb
b: acbbabdbb

This time, f [I, J] is defined as( a 0 , a 1 , . . . a i − 1 a_0,a_1,...a_{i-1} a0​,a1​,... ai − 1) and( b 0 , b 1 , . . . b j − 1 b_0,b_1,...b_{j-1} b0​,b1​,... The longest common continuous subsequence length of bj − 1), and the last character of the subsequence is a i − 1 or b i − 1 a_{i-1} or b_{i-1} ai − 1 or bi − 1, that is, this continuous subsequence is the second half of the two sequences at the same time.

This can be divided into the following three cases:

1. Boundary case f [I, J] = 0, when i=0 or j=0.
2. A [I-1] = B [J-1], continue to look forward. There is f [I, J] = f [I-1, J-1] + 1.
3. A [I-1] ≠ B [J-1], according to the definition, this continuous subsequence must end with a [I-1] or B [J-1]. Such subsequence does not exist, so there is f [I, J] = 0.

public class LCS {
	char[] a; 						// Storage sequence a
	char[] b; 						// Storage sequence b
	int[][] dp;
	int len; 						// Save maximum length
	int index; 						// Save the starting subscript of the common subsequence

	public LCS(String str1, String str2) {
		a = str1.toCharArray();
		b = str2.toCharArray();
		dp = new int[a.length + 1][b.length + 1];
	}

	public int getLenth() {
		for (int i = 1; i <= a.length; i++) {
			for (int j = 1; j <= b.length; j++) {
				if (a[i - 1] == b[j - 1]) {
					dp[i][j] = dp[i - 1][j - 1] + 1;
				}

				if (dp[i][j] > len) {
					len = dp[i][j];
					index = i - len;
				}
			}
		}
		return len;
	}

	public StringBuilder getSubSequence() {
		StringBuilder subs = new StringBuilder("");
		for (int i = 0; i < len; i++) {
			subs.append(a[index + i]);
		}
		return subs;
	}

	public static void main(String[] args) {
		String str1 = "abcbdb";
		String str2 = "acbbabdbb";
		LCS ls = new LCS(str1, str2);
		System.out.println("Length:" + ls.getLenth());
		System.out.println("Longest continuous common subsequence:" + ls.getSubSequence());
	}
}

dp array during solution:

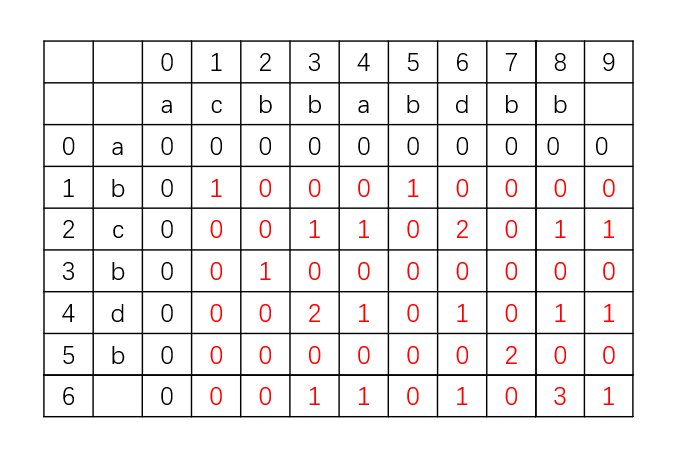
Space and time complexity are the same O ( m n ) Ο(mn) O(mn).