The three methods can be used for reference, but the code part is written by yourself. Although the final running results are correct, it is inevitable that there will be some thoughtless places in this process. If you find some errors in the code, you are welcome to correct. At the same time, new ideas can also be put forward!

The sequential structure is used to store the string, and the longest common substring of string s and string t is obtained.

Method 1

• Algorithm idea: with the help of two-dimensional array, the array subscript of the last character of the longest common substring in s string and t string can be obtained. At this time, the longest common substring can be intercepted from s or t.

SqString MaxComStr(SqString s, SqString t)
{
	SqString str;
	int arr[MaxSize][MaxSize];
	int i, j, k, maxi[2], maxlen = 0;
	for (i = 0; i < s.length; i++)
		for (j = 0; j < t.length; j++)
		{
			if (s.data[i] == t.data[j])
			{
				if (i == 0 || j == 0) arr[i][j] = 1;
				else
				{
					arr[i][j] = arr[i - 1][j - 1] + 1;
					if (arr[i][j] > maxlen)
					{
						maxlen = arr[i][j];
						maxi[0] = i;
						maxi[1] = j;
					}
					printf("\ni=%d j=%d arr=%d", i, j, arr[i][j]);
				}
			}
			else arr[i][j] = 0;
		}
			else arr[i][j] = 0;
		}
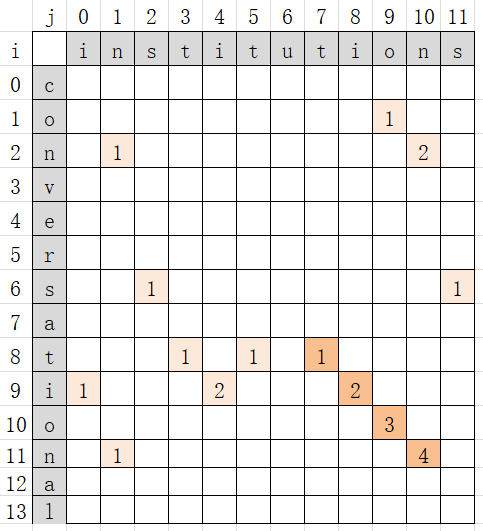
	printf("\n The line number of the maximum value in the two-dimensional array is:%d Column number is:%d\n", maxi[0], maxi[1]);
	//Output 2D array
	for (i = 0; i < s.length; i++)
	{
		for (j = 0; j < t.length; j++)
			printf("%2d", arr[i][j]);
		printf("\n");
	}
	//Select one of two common substring codes (line number interception / column number interception)
	/*for (k = maxlen - 1, i = maxi[0]; k >= 0; k--, i--) //Intercept from s string with line number
	{
		str.data[k] = s.data[i];
		str.length = maxlen;
	}*/
	for (k = maxlen - 1, i = maxi[1]; k >= 0; k--, i--) //Intercept from t string with column number
	{
		str.data[k] = t.data[i];
		str.length = maxlen;
	}
	//Output str
	printf("\n The longest common substring is:");
	DispStr(str);
	printf("\n");
	return str;
}

analysis

• Analysis: LCS (Longest Common Subsequence) algorithm

1. Construct n × M, where N and m are the lengths of s string and t string respectively.
2. Double loop nesting. If a character in the s string is equal to a character in the t string, there are two cases:
   ① At this time, if the equal characters are in the first row or column of the two-dimensional array, set arr[i][j] to 1;
   ② If ① is not satisfied, the value of this position is the value of its upper left diagonal + 1. That is, arr[i][j]=arr[i-1][j-1]+1.
3. The maximum value in the two-dimensional array is the length of the longest common substring, and its row and column subscript values are saved.
4. If the common substring is intercepted from s, the line number is used. Line number - the length of the longest common substring is the starting subscript value of the longest common substring in s string; If the common substring is intercepted from t, the column number, column number - the length of the longest common substring, is used to obtain the starting subscript value of the longest common substring in t string.
   

Operation results

• Time complexity: O(nm) (mainly used to assign values to two-dimensional arrays)
• Spatial complexity: O(nm) (a two-dimensional array is created)
  Where n and m are the lengths of s string and t string respectively.

Method 2

• Algorithm idea: brute force algorithm, also known as simple matching algorithm, is used to scan s string and t string.

SqString MaxComStr(SqString s, SqString t)
{
	SqString str;
	int i, j, count = 0, maxlen = 0, start;
	for (i = 0; i < s.length; i++)
	{
		for (j = 0; j < t.length; j++)
		{
			int start1 = i;
			int start2 = j;
			while ((start1 <= s.length - 1) && (start2 <= t.length - 1) && (s.data[start1] == t.data[start2]))
			{
				start1++;
				start2++;
				count++;
			}
			if (count > maxlen)
			{
				maxlen = count;
				start = i;
			}
			count = 0;
		}
	}
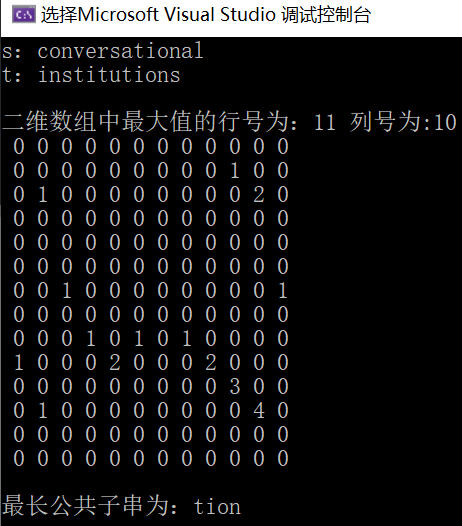
	printf("\n The starting subscript of the longest common substring is:%d Substring length:%d", start, maxlen);
	for (i = 0, j = start; i < maxlen; i++, j++)
		str.data[i] = s.data[j];
	str.length = maxlen;
	printf("\n The longest common substring is:");
	DispStr(str);
	return str;
}

analysis

1. The data[0] (character 'c') of string s is compared with each element of string t one by one. There is no same character in the first round.
   

1. The data[1] (character 'o') of string s is compared with each element of string t one by one

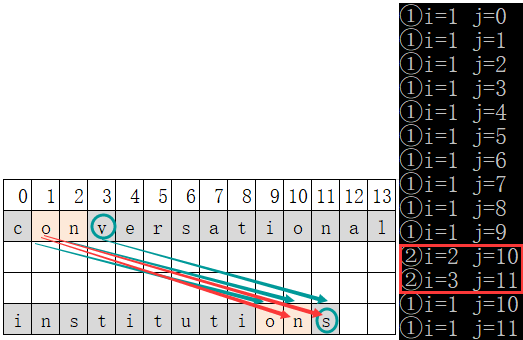
• ① It is found that the data[1] of S is equal to the character of data[9] in T. at this time, compare the string s and the next character of string t (that is, compare the data[2] (character 'n') of s with the data[10] (character 'n') of T).
• ② It is found that the two characters are still equal at this time, and then compare the next character of the two strings (i.e. data[3] (character 'v') of S and data[11] (character's') of T). At this time, it is found that the two characters are not equal. At this time, both string s and string t will not move back. Two characters in this round are equal, count=2.
• ③ Since s.data[1] and t.data[9] in ① have been compared, when comparing s.data[1] (character 'o') with t.data[10] (character 'n'), the two characters are different. When comparing s.data[1] (character 'o') with t.data[11] (character's'), the two characters are still different. At this time, the t string has reached the end and this round is over.
  

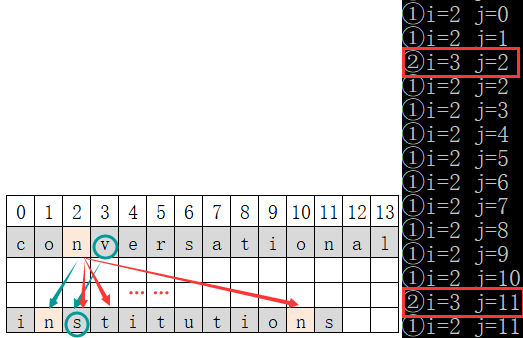
1. The data[2] (character 'n') of string s is compared with each element of string t one by one

• ① It is found that the data[2] of S is equal to the character of data[1] in T. at this time, compare the string s and the next character of string t (that is, compare the data[3] (character 'v') of s with the data[2] (character's') of T). At this time, it is found that the two characters are not equal, and neither string s nor string t will move back.
• ② Since s.data[2] and t.data[1] in ① have been compared, compare s.data[2] (character 'n') with t.data[2] (character's'), the two characters are different, and compare s.data[2] (character 'n') with t.data[11] (character't '), the two characters are still different. Continue this operation.
• ③ It is found that the data[2] of S is equal to the character of data[10] in T. at this time, compare the string s and the next character of string t (that is, compare the data[3] (character 'v') of s with the data[11] (character's') of T). At this time, it is found that the two characters are not equal, and neither string s nor string t will move back.
• ④ Since s.data[2] and t.data[10] in ③ have been compared, let s.data[2] (character 'n') compare with t.data[11] (character's'). The two characters are different. At this time, the t string has reached the end and this round is over.
  

Operation results

• Time complexity: O (nm) (time complexity of BF algorithm)
• Space complexity: O(1) (no new space is opened except str [])
  Where n and m are the lengths of s string and t string respectively.

Method 3

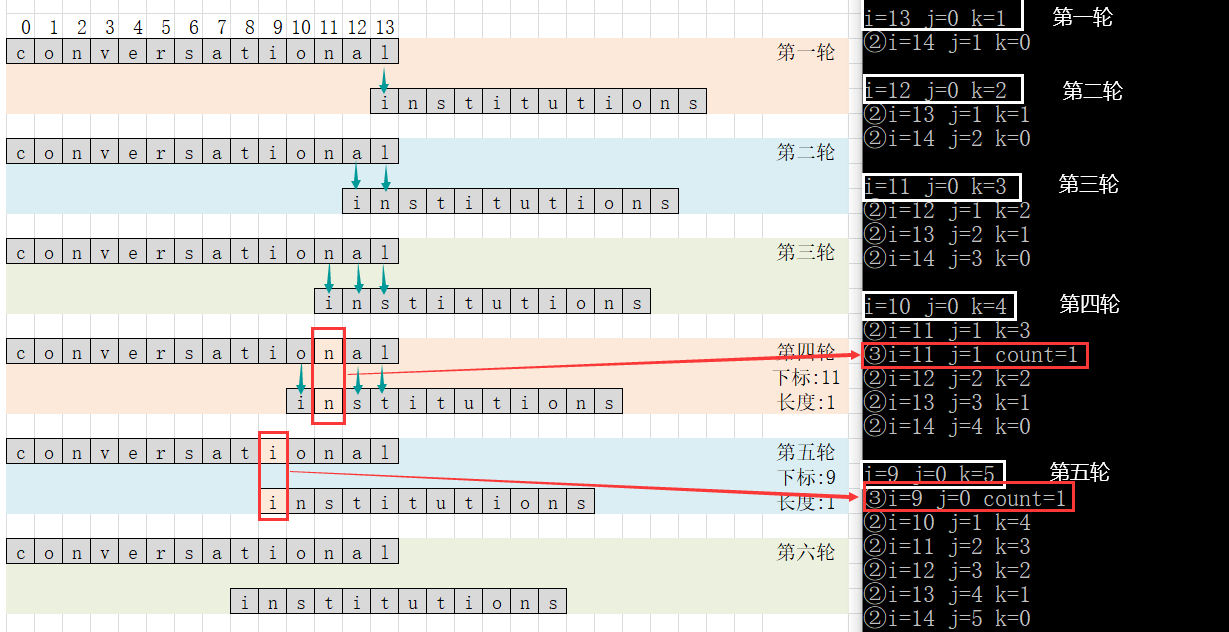
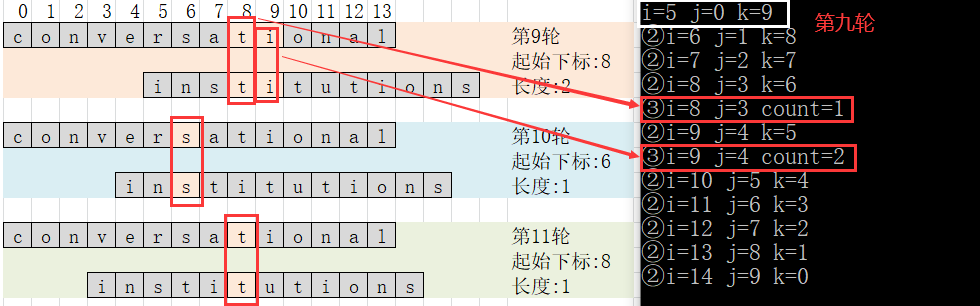
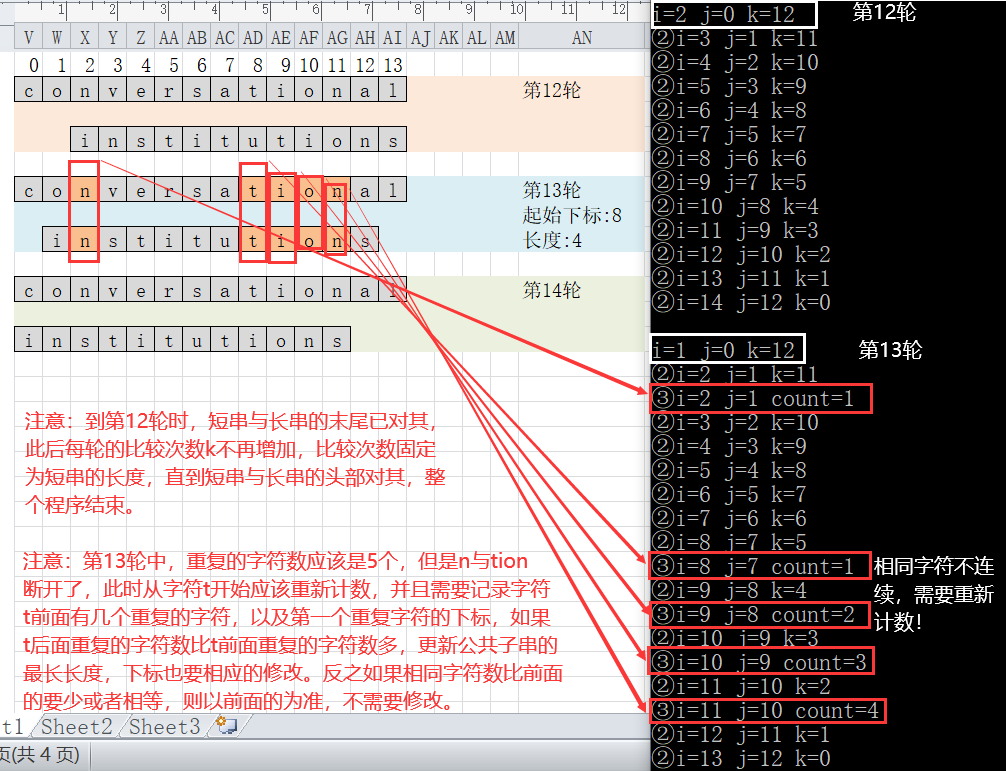
• Algorithm idea: align the head of the short string with the tail of the long string, gradually move the short string, and compare the length of the longest common substring in the overlapping string until the head of the short string is aligned with the head of the long string.

SqString MaxComStr(SqString s, SqString t)
{
	SqString str;
	int i = 0, j, k, n = 1, m = s.length;
	int count = 0, index[2] = {0,0}, num = 0;
	while (n<=s.length) //The number of cycles is determined by the long string
	{
		i = --m; //The starting subscript of the long string at the beginning of each comparison
		j = 0; //At the beginning of each comparison, the starting subscript of the short string is 0
		if (i > s.length - t.length) k = s.length - i; //If the short string tail and the long string tail are not matched, the number of comparisons required in each trip will increase in turn
		else k=t.length; //Once the short string tail and the long string tail are matched, the comparison times of each subsequent trip are determined by the short string
		while (k > 0) //k is the number of comparisons required in each trip
		{
			if (s.data[i] == t.data[j]) count++; //If the two characters corresponding vertically are equal, the length of the common substring is + 1
			i++; j++; //Compare the two characters corresponding to each vertical in turn
			if (s.data[i-1]==t.data[j-1]&&s.data[i] != t.data[j]) //If the two characters in the previous vertical direction are equal, but the two characters in the next vertical direction are not equal, that is, the characters are not continuously equal
			{
				if (count > num) //Record the longest continuous common character
				{
					num = count; //Record the length of the longest common substring before disconnection
					index[0] = i - count;  //The starting subscript of the longest common substring in the long string
					index[1] = index[0] - m; //The starting subscript of the longest common substring in the short string
				}
				count = 0; //Each time it is found that the characters are discontinuous and equal, it is necessary to count again, and then compare the length before and after disconnection to take the maximum value
			}
			k--; //For each comparison, the number of remaining comparisons is reduced
		}
		n++; //The total number of trips compared minus 1
	}
	for (i = 0, j = index[0]; i < num; i++, j++)
		str.data[i] = s.data[j];
	str.length = num;
	printf("\n The starting subscript of the longest common substring in the long string is:%d\n The starting subscript in the short string is:%d\n The length of the longest common string is:%d", index[0], index[1], num);
	printf("\n The longest common substring is:");
	DispStr(str);
	return str;
}

analysis

• The algorithm only needs to compare the corresponding positions vertically, and the diagonal positions do not need to be compared.
• As shown in the figure, s.data[12]==t.data[0] s.data[13]==t.data[1]？
• And s.data[12]==t.data[1]? Will be compared in the next round; And s.data[13]==t.data[0]? The comparison has been completed in the last round.
  
• It can be seen from the figure that a total of 14 rounds need to be compared (14 is the length of the longer string). In the worst case, the first round needs to be compared once, the second round needs to be compared twice... The twelfth round needs to be compared 12 times (at this time, the two string tails are aligned). At this time, there are two rounds to 14, and the number of comparisons of the remaining two rounds is 12 (i.e. the length of the shorter string).

Implementation steps:

1. Define a variable n (used to indicate the total number of rounds to be compared). The number of rounds to be compared is determined by the length of the long string. For each round of comparison, let n + +.
2. Define a variable m (used to represent the starting subscript of the long string to start the comparison in each round). The initial value of M is the length of the long string. In each round, reduce m by 1 before starting the comparison.
3. Define two variables i (indicating the starting subscript of the long string in each comparison) and J (indicating the starting subscript of the short string in each comparison). As can be seen from the figure, j is the comparison range of 0~m-1 every time, and i can be expressed as – m.
4. Define variable K (used to indicate the number of comparisons required in each round of cycle), start of each round of comparison, k=m, each comparison in each round, K –.
5. Define the variable count (used to count the number of repeated characters in each round)
6. Define the variables num (the length of the longest common substring) and index (the starting subscript of the longest common substring)
   
   
   

Operation results

• Time complexity: 1 + 2 + . . . + n + ( n − m ) m 1+2+...+n+(n-m)m 1+2+...+n+(n−m)m
• Space complexity: O(1)
  Where n and m are the lengths of s string and t string respectively.