Abuse you thousands of times, but also to wait for her like the first love of the red and black tree, whether she is both happy and afraid. Don't worry. I hope you will be touched by this article.
Red black tree is also a binary search tree, but it has some more characteristics than ordinary binary search tree. Each node has red or black marks. Because it's a binary search tree, it has all the features of a binary search tree. Red black tree is a kind of self balanced binary search tree, which will not degenerate into chain like data when extreme data conditions are inserted (positive order or flashback), and can more efficiently complete the search, insertion and deletion operations in O(log(n)) time.
Get ready
Before reading this article, I suggest reading my last article Interpretation and implementation of binary search tree It can help you understand the red black tree better.
Characteristic
- Node is red or black
- Root must be black
- Leaf node (Convention is null) must be black
- The number of black nodes in each path from any node to leaf node is equal
- Two consecutive nodes are not allowed to be red, that is, the parent node and the child node cannot both be red
lookup
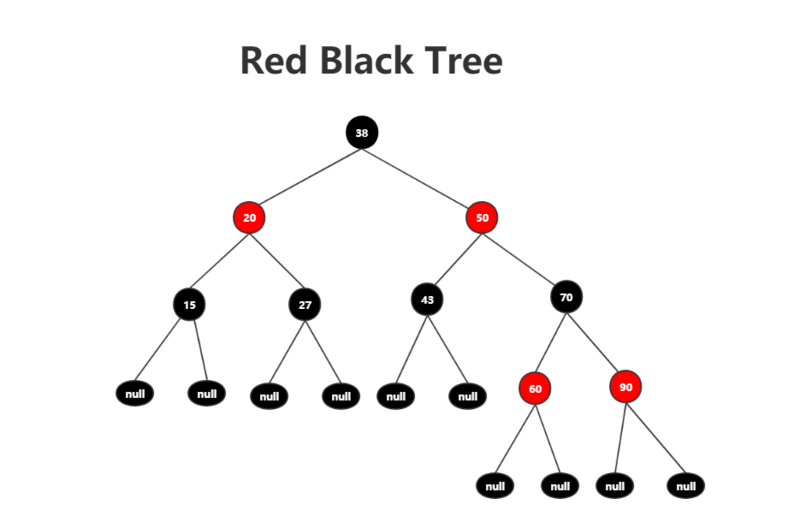
The search method of the red black tree is the same as the principle described in the previous article. We will not retell it here. Take the node [38,20,50,15,27,43,70,60,90] as an example to return a red black tree.
Ordinary operation
The insertion and deletion of red black tree can be divided into many situations, which are relatively complex. After inserting or deleting new nodes, the tree must satisfy the binary search tree of the above five characteristics, so the tree should be adjusted by different means. But ordinary operations are the same as ordinary binary search tree operations.
For example, in normal insertion, because each node can only be red or black, we define the default color of the newly added non root node as red. The reason why the new node is defined as red is to meet property 4 (the number of black nodes in each path from any node to the leaf node is equal), otherwise, another black node will break the rule.
Now insert node 10 into the tree.

It can be seen from the figure that the parent node 15 is a black node, inserting the red node 10 will not increase the number of black nodes, and other rules will not be affected. Therefore, when the parent node of the inserted node is a black node, directly inserting the tree will not destroy the rules of the original red black tree.
Code implementation in this case:
Node object
package com.ytao.rbt; /** * Created by YANGTAO on 2019/11/9 0009. */ public class Node { public static String RED = "red"; public static String BLACK = "black"; public Integer value; public String color; public Node left; public Node right; public Node(Integer value, String color, Node left, Node right) { this.value = value; this.color = color; this.left = left; this.right = right; } public Node(int value, String color) { this.value = value; this.color = color; } }
Implementation operation
public void commonInsert(Node node, Integer newVal){ if (node == null) node = new Node(newVal, Node.BLACK); while (true){ if (newVal < node.value){ if (node.left == null){ // If the left tree is a leaf node and the parent node is black, you can directly insert a new red node if (node.color == Node.BLACK){ node.left = new Node(newVal, Node.RED); break; } } node = node.left; }else if (newVal > node.value){ if (node.right == null){ if (node.color == Node.BLACK){ node.right = new Node(newVal, Node.RED); break; } } node = node.right; } } }
See whether this code is familiar or not. Yes, this is the color limit of the insertion operation in the previous article.
The same is true for deletion, which is not detailed here.
Discoloration
In order to better analyze the cause of discoloration, we extract 50 nodes from the tree as root nodes, as shown in the figure:

Add node 55 to the tree, and the tree is shown as follows:

At this time, 55 and 60 are red nodes, which do not conform to the characteristics of red black tree (it is not allowed that two consecutive nodes are red). At this time, we need to adjust and use the color change.
When we change the parent node 60 to black, we encounter the feature that does not conform to the red black tree (the number of black nodes in each path from any node to the leaf node is equal), because we increase the black node 60, and there is one more black node.
At this time, node 70 must be black, because the color of the original parent node 60 is red. The node 70 is changed to red, which satisfies the left subtree of node 70. However, the right subtree is affected by the change of node 70 to red, and there are fewer black nodes. Just when node 90 is red, it can be changed to black, which meets the right subtree requirements of node 70.
This special case is relatively simple to deal with, only through the discoloration can deal with.

The red black tree implementation of this conditional structure:
public void changeColor(Node node, int newVal){ if (node.left == null || node.right == null) return; // By judging whether the parent node and uncle node of the node to be inserted meet the conditions we need if (node.left.color == Node.RED && node.right.color == Node.RED){ // Determine whether to update to the left tree or the right tree Node base = compare(newVal, node.value) > 0 ? node.right : node.left; // Compare with the parent node of the node to be inserted if (newVal < base.value && base.left == null){ base.left = new Node(newVal, Node.RED); }else if (newVal > base.value && base.right == null){ base.right = new Node(newVal, Node.RED); } } node.color = Node.RED; // Get the uncle node of the inserted node by inverting and change the color to black Node uncleNode = compare(newVal, node.value) > 0 ? node.left : node.right; uncleNode.color = Node.BLACK; } public int compare(int o1, int o2){ if (o1 == o2) return 0; return o1 > o2 ? 1 : -1; }
rotate
When we can't solve the problem that we need to satisfy the feature simply by changing color, we should consider using the rotation of red black tree.
Rotation is often used in insertion and deletion. In order to meet our five characteristics, a new red black tree can be generated by rotation, which can be divided into left rotation and right rotation.
Left rotation
Turning left rotation to counter clockwise rotation is similar to pulling the parent node to the left (you can remember the direction of left and right rotation in this way). The transformation is shown in the figure below:

Right rotation
The right rotation is opposite to the left rotation, and the others are the same. The transformation is as shown in the figure:

It can be seen from the figure that after rotation, the parent-child relationship is reversed, and the child of the child node is given to the parent node.
If it is left rotation, the parent node will become the left child node of the rotation node, and the left child node of the child node will become the right child node of the parent node.
If it is a right rotation, the parent node will become the right child of the rotation node, and the right child of the child node will become the left child of the parent node.
It sounds rather awkward. Remember a rule. It's smaller on the left and larger on the right. It's better to understand it by combining the two rotations above.
The rotation is realized by code as follows:
/** * * @param node The parent of two rotation nodes * @param value The value of the child node of two rotation nodes, because when integrating rotation, the node can traverse and find out the value as the mark node to be rotated */ public void rotate(Node node, int value){ Node nodeChild = compare(value, node.value) > 0 ? node.right : node.left; if (nodeChild != null && value == nodeChild.value){ Node parent = node; // If the rotation child node is smaller than the rotation parent node, it performs right rotation, otherwise it is left rotation if (value < node.value){ rightRotate(parent); }else if (value > node.value){ leftRotate(parent); } } } /** * Left rotation * @param node Rotation parent */ public void leftRotate(Node node){ Node rightNode = node.right; // Left child of rotation node to right child of parent node node.right = rightNode.left; // Parent as left child of child rightNode.left = node; } /** * Right rotation * @param node */ public void rightRotate(Node node){ Node leftNode = node.left; // Right child of rotation node to left child of parent node node.left = leftNode.right; // Parent as right child of child leftNode.right = node; }
Case application of rotating color change
Insert node 55 in red and black with node 38 above. After applying the color change described above, the structure of the red black tree is as shown in the figure:

At this time, the red black tree feature is not satisfied (two consecutive nodes are not allowed to be red). At this time, we need to rotate node 50 and node 38 to the left, as shown in the following figure:

The root node 50 does not conform to the red black tree feature (the root node must be black), so first change the root node to black.

Now we get the red black tree, which violates the property that the number of black nodes in each path from any node to the leaf node is equal. The left tree has one more black node than the right tree. At this time, the color of 38, 20, 15, 27 will be changed.

Here through the color change rotation completed the above lesson tree operation red black tree adjustment.
Due to the large size of the code, not all the possible situations are taken into account. I believe that understanding of the red black tree is not too big a problem for coding implementation.
summary
The operation of red black tree is based on the characteristics of the red and black tree added to the ordinary two fork search tree, whether it is insert or delete operation, that is, the rotated color changing tree structure on the common red and black tree, so when we understand the red and black tree, we mainly grasp the rotation and discoloration, and use the color changing to meet the characteristics of the red black tree. This is also the essence of the red black tree. If you know its principle and design idea, it is a good design to solve problems in practice. Of course, the actual operation process of red black tree is variable and complex. To master it completely or to spend some time to study it.
Personal blog: https://ytao.top
My public address ytao