https://blog.csdn.net/y1196645376/article/details/94348873

1. Characteristics of table

1. In Lua, table is a very important type. Many data structures can be realized by using some features of table, such as map, array, queue, stack, etc.
2. From the perspective of users, table can be used as both array and map. For designers, it is necessary to ensure the efficient search, insertion and traversal of table.
3. Of course, the designer of table also proposed the concept of metatable, which can be used by users to implement inheritance, operator overloading and other designs. However, metatable is not discussed in this article for the time being.

2. Definition of table

typedef union TKey {
  struct {
    TValuefields;
    int next;  /* Used to mark the next node in the linked list */
  } nk;
  TValue tvk;
} TKey;

typedef struct Node {
  TValue i_val;
  TKey i_key;
} Node;


typedef struct Table {
  CommonHeader;
  lu_byte flags;  /* 1<<p means tagmethod(p) is not present */
  lu_byte lsizenode;  /* log2 of size of 'node' array */
  unsigned int sizearray;  /* size of 'array' array */
  TValue *array;  /* array part */
  Node *node;
  Node *lastfree;  /* any free position is before this position */
  struct Table *metatable;
  GCObject *gclist;
} Table;

• flags: the tag of meta method, which is used to query whether the table contains meta methods of a certain category
• Lsizenode: (1 < < lsizenode) indicates the size of the hash part of the table
• Sizearray: the size of the array part of the table
• Array: the first node of the array of table
• Node: the first node of the hash table of the table
• lastfree: indicates the cursor of the idle node of the hash table of the table
• metatable: meta table
• gclist: table gc related parameters
   

In order to improve the efficiency of table insertion and search, the combination of array array and hashtable (hash table) is adopted in the design of table.

Therefore, table will put some shaping keys as subscripts in the array, and the rest shaping keys and other types of keys in the hash table.

3.hash table structure

In the implementation of table, hash table accounts for most of the proportion. The following is the structure diagram of hash table in table:

hash table has two common methods in conflict resolution:

• Open addressing: when a conflict occurs, a probe (also known as probe) technique is used to form a probe (test) sequence in the hash table. Search cell by cell along this sequence until a given keyword is found, or an open address is encountered (that is, the address cell is empty) (to insert, the new node to be inserted can be saved in the address cell when the open address is detected). If an open address is detected during search, it indicates that there are no keywords to be checked in the table, that is, the search fails.
• Chain address method: also known as zipper method, all nodes whose keywords are synonyms are linked in the same single chain list. If the length of the selected hash table is m, the hash table can be defined as a pointer array T[0... m-1] composed of M header pointers. All nodes with hash address I are inserted into the single linked list with T[i] as the head pointer. The initial value of each component in t shall be a null pointer. In the zipper method, the filling factor α Can be greater than 1, but generally take α ≤1.

The advantages and disadvantages of the above two methods can be found by simple comparison:

  open addressing method saves more memory than chain addressing method, but it has higher complexity in insertion and search.

However, the implementation of hash table in table combines some features of the above two methods:

• Find and insert equivalent chain address method complexity.
• The memory overhead is approximately equivalent to the open addressing method.

The reason is that although the hash table in the table uses the form of chain address method to deal with conflicts, the additional nodes in the linked list are the nodes in the hash table, and there is no need to open up additional linked list nodes; The following is an introduction to TKey structure:

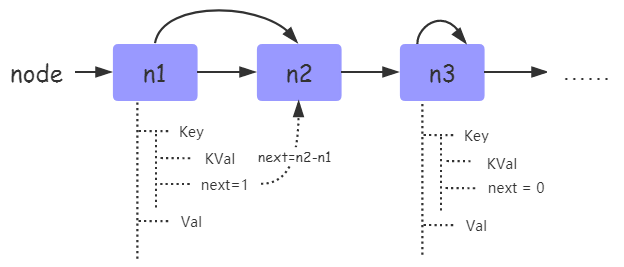
So how to use the spare nodes of the hash table as the nodes of the linked list? The implementation of this algorithm benefits from the function of lastfree pointer, which will be described in detail later

4. Creation of table

Via luah in lua_ New to create a new table:

Table *luaH_new (lua_State *L) {
  GCObject *o = luaC_newobj(L, LUA_TTABLE, sizeof(Table));
  Table *t = gco2t(o);
  t->metatable = NULL;
  t->flags = cast_byte(~0);
  t->array = NULL;
  t->sizearray = 0;
  setnodevector(L, t, 0);
  return t;
}

At this time, the array part and hash part of the table are empty.

5.luaH_get analysis

Use this function in table to find the value corresponding to key from the table; You can see that it will be processed differently through different types of keys.

const TValue *luaH_get (Table *t, const TValue *key) {
  switch (ttype(key)) {
    case LUA_TSHRSTR: return luaH_getshortstr(t, tsvalue(key));
    case LUA_TNUMINT: return luaH_getint(t, ivalue(key));
    case LUA_TNIL: return luaO_nilobject;
    case LUA_TNUMFLT: {
      lua_Integer k;
      if (luaV_tointeger(key, &k, 0)) /* index is int? */
        return luaH_getint(t, k);  /* use specialized version */
      /* else... */
    }  /* FALLTHROUGH */
    default:
      return getgeneric(t, key);
  }
}

• If the key is nil, nil is returned directly.
• If the key is an integer class, luah is called_ GetInt, because the integer key may be taken in the array.
• If the key is a floating-point number, first judge whether the key can be converted to an integer. If so, call luaH_getint, otherwise call getgeneric.
• If the key is a short string type, luah is called_ Getshortstr. (in fact, this case is a little incomprehensible. Short strings can also be handled by getgeneric)
• Other types of key s are processed using getgeneric.
   

The following focuses on the analysis of luah_ The processes of getInt and getgeneric functions.

luaH_getint

const TValue *luaH_getint (Table *t, lua_Integer key) {
  /* (1 <= key && key <= t->sizearray) */
  if (l_castS2U(key) - 1 < t->sizearray)
    return &t->array[key - 1];
  else {
    Node *n = hashint(t, key);
    for (;;) {  /* check whether 'key' is somewhere in the chain */
      if (ttisinteger(gkey(n)) && ivalue(gkey(n)) == key)
        return gval(n);  /* that's it */
      else {
        int nx = gnext(n);
        if (nx == 0) break;
        n += nx;
      }
    }
    return luaO_nilobject;
  }
}

As mentioned earlier, table is composed of array and hashtable, so for the shaped key, you need to find it in the array range first:

• If the size of the key is within the size range of the array, you can directly find the value in the array and return it.
• Otherwise, get the hashlot corresponding to the hash value of int, and then find the value corresponding to the key on the slot link and return it. (the search is the same as the chain address method)
• If not found, nil is returned.

getgeneric

static const TValue *getgeneric (Table *t, const TValue *key) {
  Node *n = mainposition(t, key);
  for (;;) {  /* check whether 'key' is somewhere in the chain */
    if (luaV_rawequalobj(gkey(n), key))
      return gval(n);  /* that's it */
    else {
      int nx = gnext(n);
      if (nx == 0)
        return luaO_nilobject;  /* not found */
      n += nx;
    }
  }
}

In fact, the getgeneric process is the traditional chain address search process, but it is worth noting that the mainposition function distinguishes lua's hash methods for various types:

static Node *mainposition (const Table *t, const TValue *key) {
  switch (ttype(key)) {
    case LUA_TNUMINT:
      return hashint(t, ivalue(key));
    case LUA_TNUMFLT:
      return hashmod(t, l_hashfloat(fltvalue(key)));
    case LUA_TSHRSTR:
      return hashstr(t, tsvalue(key));
    case LUA_TLNGSTR:
      return hashpow2(t, luaS_hashlongstr(tsvalue(key)));
    case LUA_TBOOLEAN:
      return hashboolean(t, bvalue(key));
    case LUA_TLIGHTUSERDATA:
      return hashpointer(t, pvalue(key));
    case LUA_TLCF:
      return hashpointer(t, fvalue(key));
    default:
      lua_assert(!ttisdeadkey(key));
      return hashpointer(t, gcvalue(key));
  }
}

Mainposition is the hash value% the size of the hash table.
It is worth noting that for the hash processing of strings, lua distinguishes between long strings and short strings (after 5.3, strings are distinguished according to their length)

• For short strings, lua is stored in stringtable, so there is only one entity for short strings. You can directly use the hash value of string in stringtable.
• For long strings, there may be multiple instances in lua, so you need to pass luaS_hash to calculate its hash value.

6.luaH_set analysis

TValue *luaH_set (lua_State *L, Table *t, const TValue *key) {
  const TValue *p = luaH_get(t, key);
  if (p != luaO_nilobject)
    return cast(TValue *, p);
  else return luaH_newkey(L, t, key);
}

luaH_set is not a set in the traditional sense, that is, directly pass in the key and value and then set, but the incoming key will return the TValue corresponding to the key, and then set the TValue through setobj2t. So the set function is very simple:

• Call luah first_ Get finds whether the key already exists in the table. If yes, it returns directly.
• Otherwise, luah is called_ Newkey creates a key and returns the corresponding TValue. (note that the key must not be in the array at this time)

So luah_ The analysis of set is transformed into luah_ Analysis of newkey:

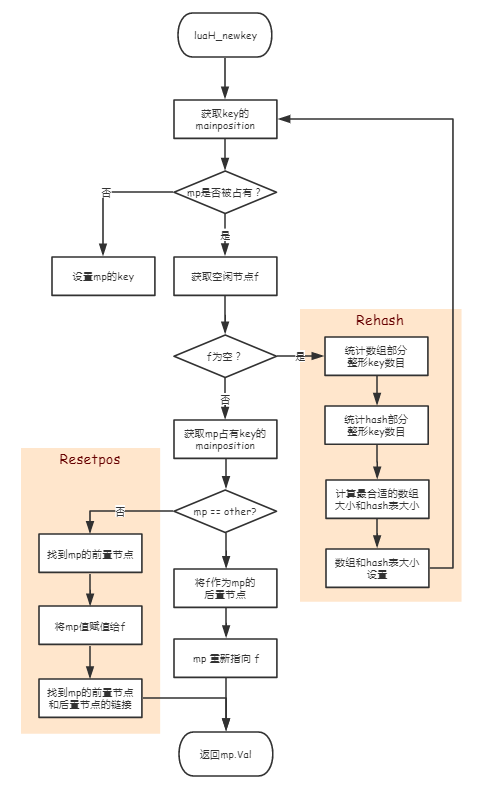
Looking at the flow chart is a little complicated. The following is a practical example (excluding Rehash):

//Assume that the default size of tb's hash table is 8 elements
local tb = {}
tb[3] = 'a'
tb[11] = 'b'
tb[19] = 'c'
tb[6] = 'd'
tb[14] = 'e'

1. After executing local tb = {}, the hash table status in tb is as follows:

The spare node pointer lastfree points to the last node.

Note: the default hash table size of table creation is 0. Here, for convenience of description, assume that the initial size is 8, so you don't have to worry about the rehash part

2. After tb [3] ='a 'is executed, the hash table status in tb is as follows:

Because the mainposition of 3 is 3, it is placed in the n3 position.

Note: the manposition of the key is equal to hash(k)%table_size, so mainposition(3)=3%8

3. After tb [11] ='b 'is executed, the hash table status in tb is as follows:

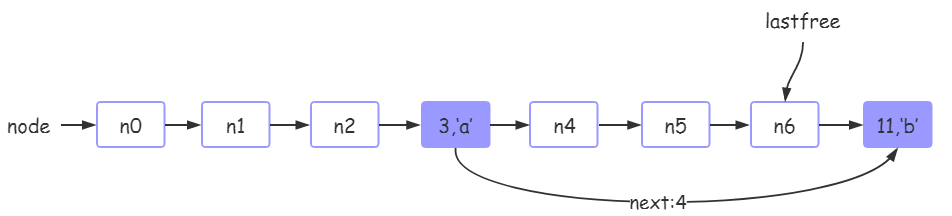Because the mainposition of 11 is also 3, but the position 3 has been occupied, at this time, use lastfree to obtain an empty node n7, store the current key in the position n7, and insert the n7 node after the mainposition node n3 using the header insertion method, so the next = n7 - n3 = 4 here.

4. After tb [19] ='c 'is executed, the hash table status in tb is as follows:

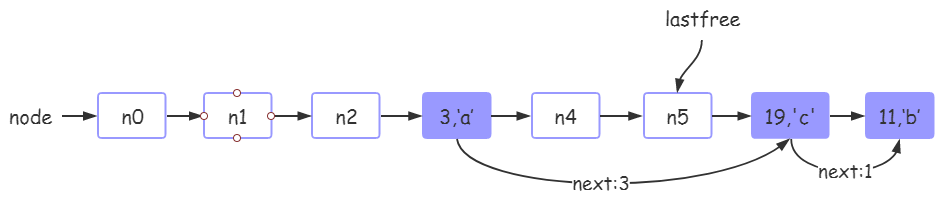
The reason is similar to the above, but note that 19 is inserted between the mainposition node n3 and the next node n7 of mp, so the next value of n3 needs to be maintained again.

5. After tb [6] ='d 'is executed, the hash table status in tb is as follows:

In this step, there are some different processes. First, calculate the mainposition of 6 as 6, and then find that n6 has been occupied by key:19. However, at this time, we cannot directly use lastfree to store key:6, because 19 and 6 are not on the same linked list, that is, key:19 robbed the position of key:6:

mainpositon(19)=19

mainpositon(6)=6

In this case, we need to give up the position of key:19, apply for an empty node n5 through lastfree, and then change the position of 19 to n5 (pay attention to maintaining the next node). Then put key:6 on the n6 node.

This part of the operation is the Resetpos part of the flowchart

6. After tb [14] ='e 'is executed, the hash table status in tb is as follows:

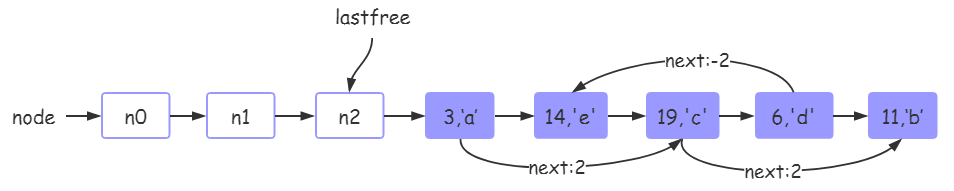
This is similar to step 3.

Let's analyze Rehash:

Rehash does not necessarily represent the expansion of the hash table, but re allocate the size of the array and the size of the hash table more appropriately according to the number and type of key s in the table. The capacity may be expanded, unchanged or reduced.

If the status of array and hash tables in the table is as follows: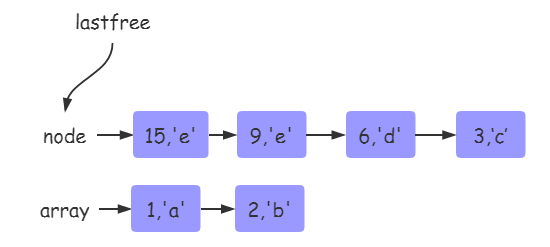

At this time, insert another key:10. Because lastfree can no longer obtain empty nodes, rehash is triggered.

• First, calculate the number of all integers whose val is not nil in the array part through numusarray, and num []. For nums[i] = j, its meaning means that the key is between 2^i-1 and 2^i, and the number of integer keys has j.
• Then, calculate all the integer numbers of hash part Val not nil through numusehash, and num [].
• The size of the array is determined by the number of shaping keys. Here, there is a rule to determine the size of the array, which is to meet the power size of 2, and the number of shaping keys num > arraySize / 2. It is also necessary to ensure that the number of shaping keys is higher than arraySize / 2.
• Finally, the size of the hash table is determined according to the size of the array and the total number of key s. (ps: the size of the hash table can only be a power of 2. If not, it will be aligned upward)
   

According to the above rules, it can be calculated that the size of the array part is 4 and the size of the hash table is 7 - 3 = 4. (7 refers to the total number of keys, and 3 refers to the number of keys that can be put into the array)

Whether the rehash of array or the rehash of hash table is to open up new memory first, and then reinsert the original elements.

The status after inserting key:10 is:

 

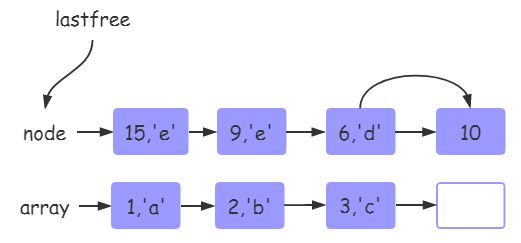
It is worth noting that the deletion of table element is realized through table[key] = nil. However, through the above analysis of luah_ We can know from the introduction of set that we only set the val corresponding to the key to nil, and do not really delete the key from the table. It may be overwritten or cleared only when a new key or rehash is inserted.
 

8.luaH_getn analysis

The length of a table in lua is usually obtained by using # operators, but here is not the length of the array part of the table, but the continuous length of the table integer key index sequence. In other words, if we treat talk as an array, the length of the array is returned when we use it. For example:

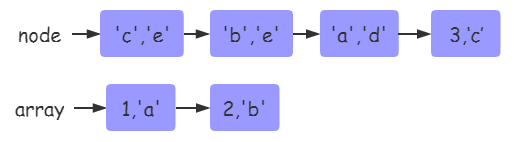
In the table shown in the figure above, there are six keys: 1, 2, 3, 'a', 'b', 'c'. Although there are only two keys in the array, the length of the table is 3, because the continuous length of the integer key is 1, 2, 3.  

It is worth noting that if an interrupt occurs in the middle of the integer key sequence, the length taken out is "uncertain"

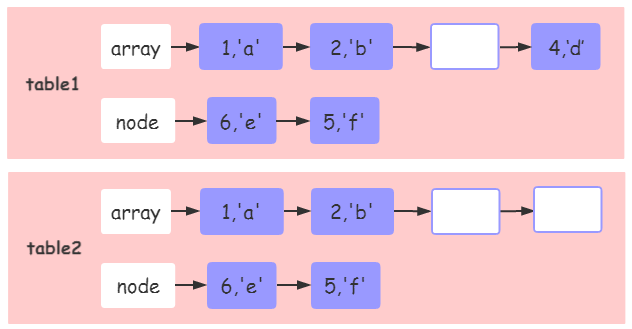
In the above two figures table1 and table2, the array part and hash part of table are integer key s. Although the index sequence is interrupted at 3 places, the length values of table1 and table2 are 6 and 2 respectively. In principle, the length of two tables should be 2, but why is there a strange "wrong value" of 6?

The root cause is caused by the algorithm of taking the length of table, and luaH_getn is a function used to find the length value of table. Let's look at the source code of this function:

int luaH_getn (Table *t) {
  unsigned int j = t->sizearray;
  if (j > 0 && ttisnil(&t->array[j - 1])) {
    /* there is a boundary in the array part: (binary) search for it */
    unsigned int i = 0;
    while (j - i > 1) {
      unsigned int m = (i+j)/2;
      if (ttisnil(&t->array[m - 1])) j = m;
      else i = m;
    }
    return i;
  }
  /* else must find a boundary in hash part */
  else if (isdummy(t))  /* hash part is empty? */
    return j;  /* that is easy... */
  else return unbound_search(t, j);
}
static int unbound_search (Table *t, unsigned int j) {
  unsigned int i = j;  /* i is zero or a present index */
  j++;
  /* find 'i' and 'j' such that i is present and j is not */
  while (!ttisnil(luaH_getint(t, j))) {
    i = j;
    if (j > cast(unsigned int, MAX_INT)/2) {  /* overflow? */
      /* table was built with bad purposes: resort to linear search */
      i = 1;
      while (!ttisnil(luaH_getint(t, i))) i++;
      return i - 1;
    }
    j *= 2;
  }
  /* now do a binary search between them */
  while (j - i > 1) {
    unsigned int m = (i+j)/2;
    if (ttisnil(luaH_getint(t, m))) j = m;
    else i = m;
  }
  return i;
}

lua is taking the length value of table. In fact, lua is looking for an integer key. It meets the following requirements

• table[key] != nil
• table[key+1] == nil

Once such a key is found, the key will be recognized as the length of the table.

In order to improve the search efficiency, lua source code does not perform traversal search, but through binary search. (time complexity reduced from O(n) to O(logn))
The specific algorithm flow is as follows:

• If the last element of the table array part is nil, a binary search will be performed in the array part
• If the last element of the table array part is not nil, a binary search will be performed in the hash part

It can be seen that the difference between the above two examples is that table[4] as the last element of the array part causes the two tables to find key s in the array part and hash part respectively.

9. Implement a LuaTable in C #

Refer to lua5 The source code of 3 LuaTable implements a LuaTable in c#
Address: https://github.com/YzlCoder/LuaTable