1, Title Description

2, Problem solving ideas
Originally, the simple Kruskal algorithm timed out. After watching the method of the great gods, I learned the chain forward star and multiplication LCA for the first time. The following chain forward star and multiplication LCA are introduced in detail below
3, Chain forward star
Chained forward star is a method to speed up dense graph search. It is an optimization based on adjacency list. Its storage structure is as follows:
struct node
{
int to;
int next;
}edge[maxv];
To represents the end point of the edge, and next represents the index of the previous edge in the edge that is the same as the starting point of the edge. Therefore, the next problem to be solved is how to find the position of the previous one in the edge. You can add an additional array head[i] to record the position of the nearest edge starting from I in the edge. Head is initialized to 0. Therefore, the functions of mapping are as follows:
struct node
{
int to;
int next;
}edge[maxv];
int head[maxn];
int cnt=1;//Indicates the subscript of the edge array, or the number of edges that have been stored
void add(int from,int t)
{
edge[cnt].to=t;
edge[cnt].next=head[from];
head[from]=cnt++;
}
We assume that the order of the input edges is < 1,2 > < 1,3 > < 2,3 >:
① When < 1,2 > is entered, edge [1] to=2,edge[1].next=head[1]=0,head[1]=1;
② When < 1,3 > is entered, edge [2] to=3,edge[2].next=head[1]=1,head[1]=2;
③ When < 2,3 > is entered, edge [3] to=3,edge[3].next=head[2]=0,head[2]=3.
The traversal process of chained forward star is illustrated by dfs. The code is as follows:
void dfs(int start)
{
vis[start]=true;
for(int i=head[start];i!=0;i=edge[i].next)
{ //When i==0, it means that there are no accessible edges starting from start
if(!vis[edge[i].to])
dfs(edge[i].to);
}
}
3, Multiplication LCA
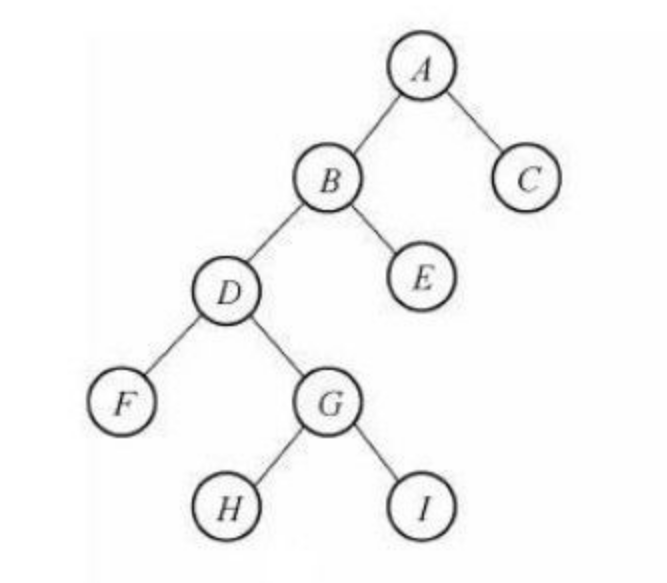
LCA is the nearest common ancestor. For example, the nearest common ancestor of F and E in the figure is B. If we want to find the nearest common ancestor of point H and point E, a simple idea is to jump up point H step by step. When we jump to the same depth as point E, compare whether the point we jump to is point E. unfortunately, we jump to point D. At this time, we should divide the soldiers into two ways, jump up from point D and point e at the same time, and compare whether each jump jumps to the same point. If it is the same point, then this point is the LCA of both, otherwise we need to continue to jump up. But it's too slow to jump up step by step. Is there any way to speed up? Binary optimization! Binary optimization is really a good thing. The multiple knapsack problem learned last time can also use binary optimization.
Now we add a two-dimensional array dp[i][j], which represents the node where the ith node jumps up 2j. The principle of binary optimization is that any positive integer can be expressed as the sum of several 2k (k=0,1,2,...). After analysis, we can easily get the following equation: dp[i][j] = DP [dp[i][j-1] [J-1]. Therefore, our initialization function can be expressed as
//fa represents the parent node of each point
int fa[100],DP[100][20];
void init()
{
//n is the number of nodes. Initialize DP array first
for(int i=1;i<=n;i++)
dp[i][0]=fa[i];
//The whole DP array is obtained by dynamic programming
for(int j=1;i<20;j++) //Generally, there will be no more than 2 ^ 20 layers of trees in the title, right? Temporarily set to 20
for(int i=1;i<=n;i++)
DP[i][j]=DP[DP[i][j-1]][j-1];
}
The code for looking for LCA is as follows
//Query function
int LCA(int a,int b)
{
//Ensure that the depth of a is greater than that of b for later operation.
if(deep[a]<deep[b])
swap(a,b);
//Let a keep jumping up until it is at the same depth as b
//If you cannot ensure that the depth of a is greater than b, you cannot determine whether it is a or b that jumps up in this step
for(int i=19;i>=0;i--)
{
//Jumping up is the process of depth reduction
if(deep[a]-1<<i>=deep[b])
a=dp[a][i];
}
//If they are at the same depth and just meet, this point is LCA
if(a==b)
return a;
//a and b jump up at the same time, traverse the step size from large to small, jump up when it is appropriate, and reduce the step size if it is not appropriate
for(int i=19;i>=0;i--)
{
//If the two don't meet, jump up
if(dp[a][i]!=dp[b][i])
{
a=dp[a][i];
b=dp[b][i];
}
}
//Finally, a and b jump to the next layer of LCA, which is the parent node of a and b
return dp[a][0];
}
4, AC code
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#define MAXN 10005
#define INF 999999999
using namespace std;
struct Edge1 {
int x, y, dis;
}edge1[50005]; //The picture given by the title
struct Edge2 {
int to, next, w;
}edge2[100005]; //Graph of maximum spanning tree
int cnt, n, m, head[MAXN], deep[MAXN], f[MAXN], fa[MAXN][21], w[MAXN][21];
bool vis[MAXN] = { false };
void addedge(int from, int to, int w)
{ //Forward star map
edge2[++cnt].next = head[from]; //Index of the previous edge stored at the same starting point
edge2[cnt].to = to; //Deposit destination
edge2[cnt].w = w;
head[from] = cnt;
return;
}
bool CMP(Edge1 x, Edge1 y)
{
return y.dis < x.dis; //Sort edge weights from large to small
}
int find(int x) {
if (f[x] != x) f[x] = find(f[x]);
return f[x];
}
void kruskal()
{
sort(edge1 + 1, edge1 + m + 1, CMP);
for (int i = 1; i <= n; i++)
f[i] = i; //Parallel query set initialization
for (int i = 1; i <= m; i++)
if (find(edge1[i].x) != find(edge1[i].y)) {
f[find(edge1[i].x)] = find(edge1[i].y);
addedge(edge1[i].x, edge1[i].y, edge1[i].dis);
addedge(edge1[i].y, edge1[i].x, edge1[i].dis); //Undirected graph, two-way edge
}
return;
}
void dfs(int node)
{
vis[node] = true;
for (int i = head[node]; i; i = edge2[i].next) { //Forward star traversal
int to = edge2[i].to;
if (vis[to]) continue;
deep[to] = deep[node] + 1; //Calculation depth
fa[to][0] = node; //Save parent node
w[to][0] = edge2[i].w; //Weight stored to parent node
dfs(to);
}
return;
}
int lca(int x, int y)
{
if (find(x) != find(y)) return -1; //Disconnected, output - 1
int ans = INF;
if (deep[x] > deep[y]) swap(x, y); //Ensure that the y node is deeper
for (int i = 20; i >= 0; i--)
if (deep[fa[y][i]] >= deep[x]) {
ans = min(ans, w[y][i]); //Update maximum load (minimum edge weight)
y = fa[y][i]; //y is the jumping position
}
if (x == y) return ans; //If the positions are already equal, return the answer directly
//Looking for common ancestors
for (int i = 20; i >= 0; i--)
if (fa[x][i] != fa[y][i]) {
ans = min(ans, min(w[x][i], w[y][i])); //Update maximum load (minimum edge weight)
x = fa[x][i];
y = fa[y][i]; //Modify x,y position
}
ans = min(ans, min(w[x][0], w[y][0]));
//Update X and y to the maximum load of the common ancestor at this time, fa[x][0], fa[y][0] is the common ancestor
return ans;
}
int main()
{
int x, y, z, q;
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", &x, &y, &z);
edge1[i].x = x;
edge1[i].y = y;
edge1[i].dis = z;
} //Save the picture given by the title
kruskal();
for (int i = 1; i <= n; i++) //It is not necessarily a connected graph, so each point needs to be collected
if (!vis[i]) { //dfs collects information
deep[i] = 1;
dfs(i);
fa[i][0] = i;
w[i][0] = INF;
}
//LCA initialization
for (int i = 1; i <= 20; i++)
for (int j = 1; j <= n; j++) {
fa[j][i] = fa[fa[j][i - 1]][i - 1];
w[j][i] = min(w[j][i - 1], w[fa[j][i - 1]][i - 1]);
}
scanf("%d", &q);
for (int i = 1; i <= q; i++) {
scanf("%d%d", &x, &y);
printf("%d\n", lca(x, y)); //Answer questions
}
return 0;
}