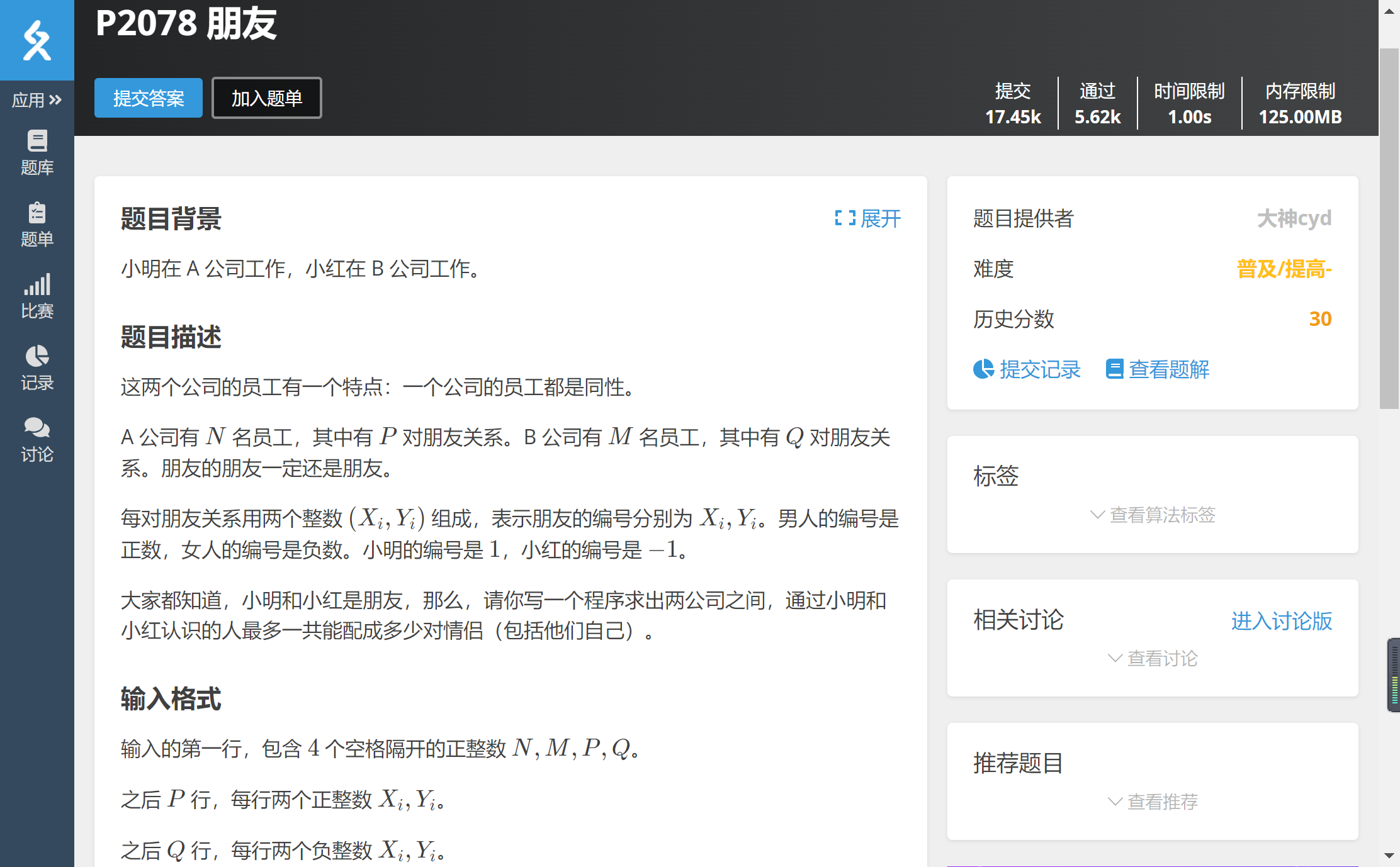
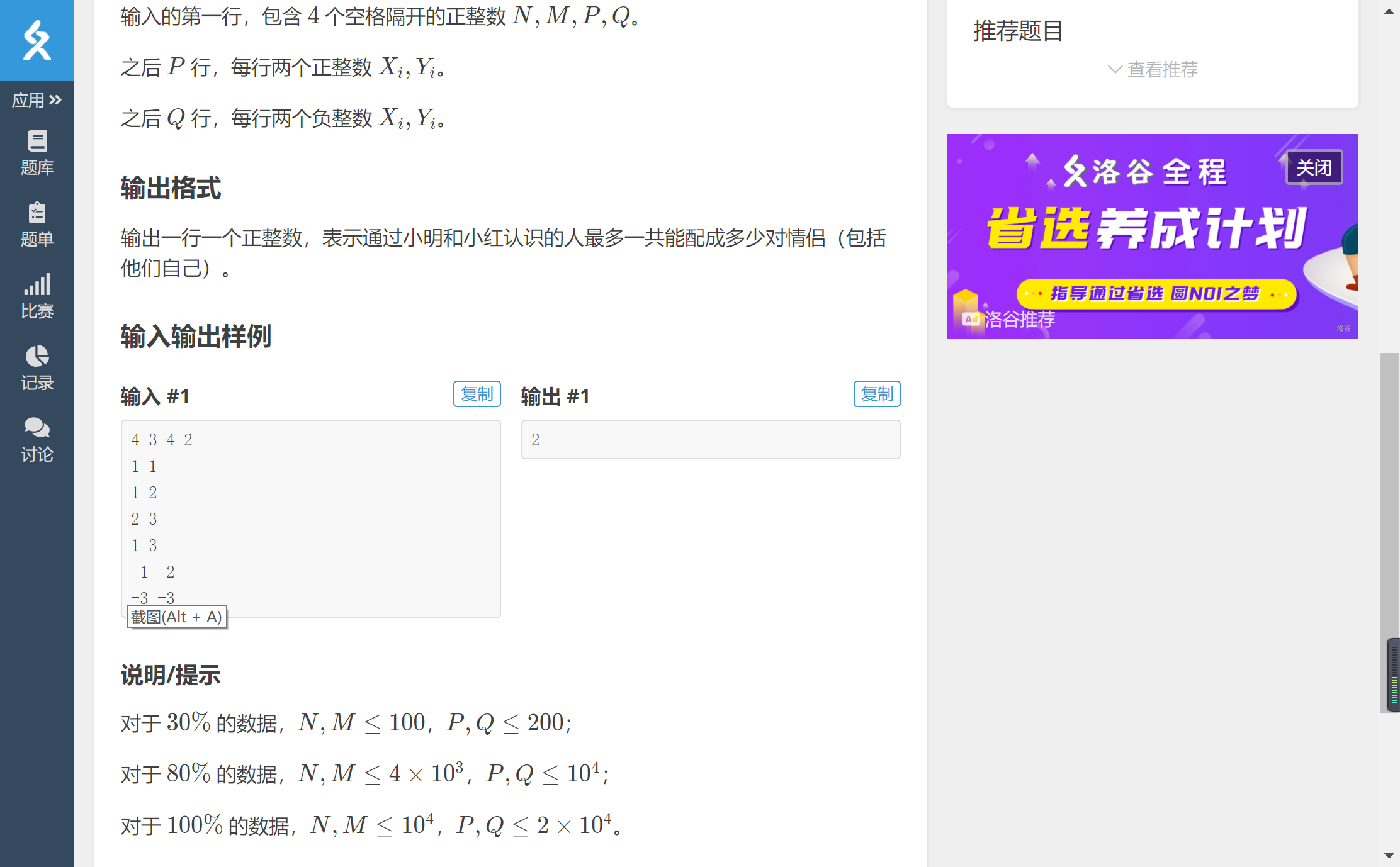
The idea is to divide into two parallel search sets, then calculate the number of men and women, and then directly compare them and choose the smaller one
The code is a little troublesome. It seems that it hasn't been handed in, although the result is right
In fact, a problem has been found in the first time, because the less than sign is accidentally marked as greater than sign during comparison, and then the man with more friends is output, but the result is actually 5. It is indeed wrong to hand it in. After the second time, the code continues to try the man. It is right, 3, but it is still unexpected 30
Think about it as if you want to consider the minus sign. After all, the array has no a[-1], but has been changed to
combine_2(abs(x2),abs(y2));
With the absolute value added, it's still wrong to hand it in. It's a little annoying
I really can't think of anything wrong. A few minutes later, I drew a boring picture. Oh, Huo, I suddenly found that men and women in other people are not necessarily friends, because Xiaoming and Xiaohong are friends, but if one party forms n pairs of friends, but that bunch of people are not friends with Xiaoming, it doesn't work to count with cnt. In the end, there is only one pair, So after counting, make sure that there are Xiaoming and Xiaohong in the two Tuos, otherwise there will be only one pair. Once again, I had third times, but I only had three test points, and it was no problem to test many different situations.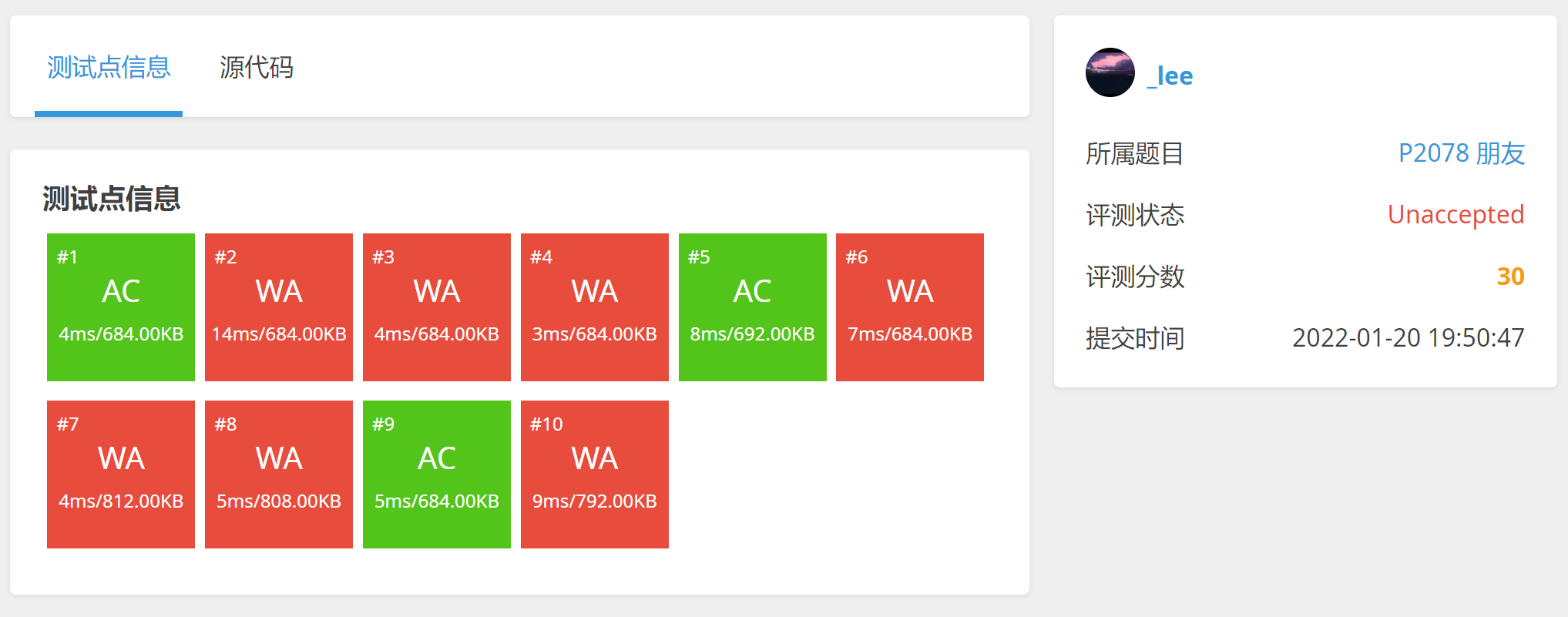
It took a long time to come back from the bath.. I also realized that if the relationship is connected, it is equivalent to the combination of sets. cnt counts + 1, but it is not enough to only check that 1 or - 1 is not in it. If there are several large sets, but they are not merged, but cnt has + 1 every time small sets are merged into large sets, so if only one or several large sets are merged with 1, it will not work, In that way, cnt counts the number of people in all large sets (including large sets without 1). Then you still have to go back to the root node to write code.
Think again:
1. It is still divided into two parallel query sets, and the relationship is connected first;
2. Starting from the two root nodes, traverse to find how many nodes there are respectively;
3. Compare the number of nodes and output smaller ones.
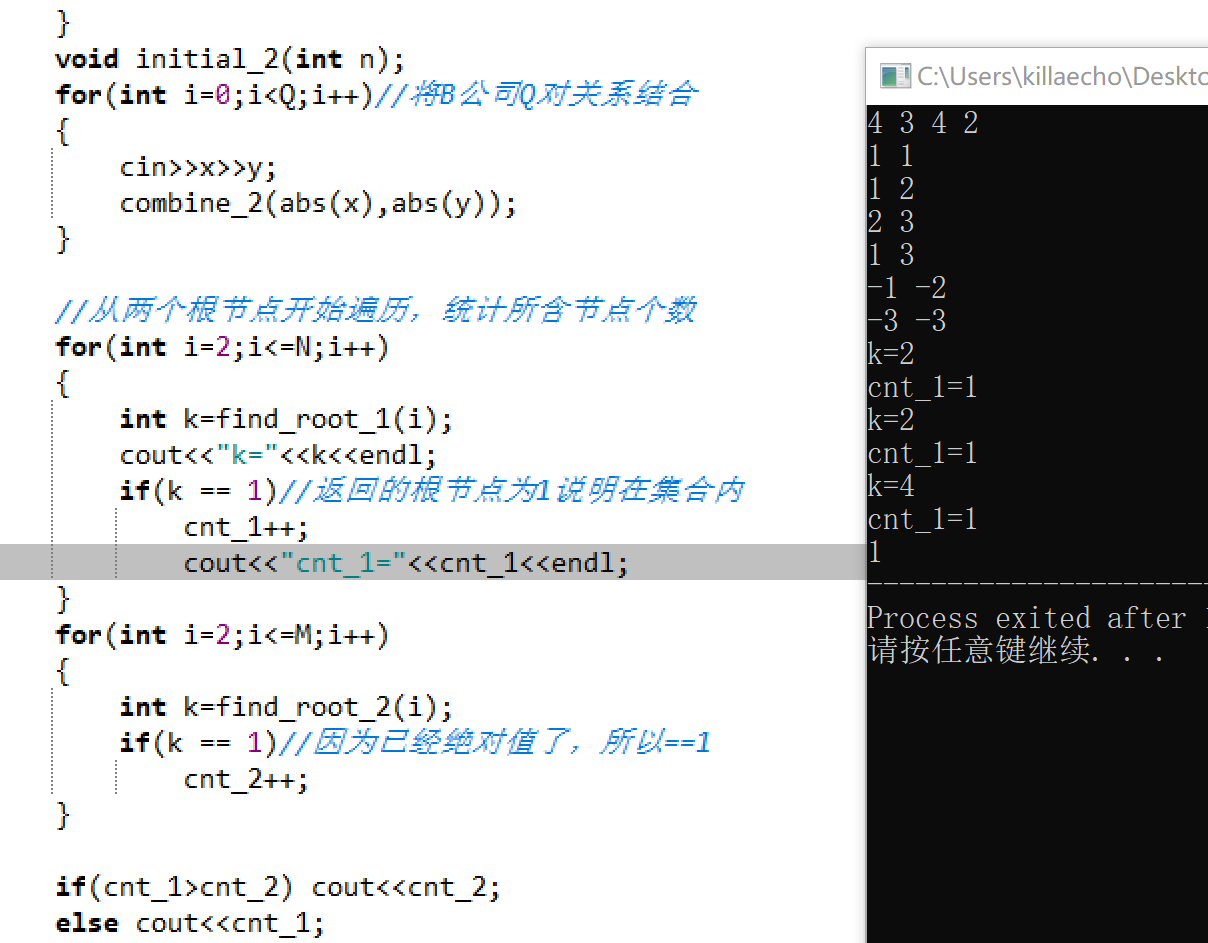
Here, because they are not connected in an ideal way, their root node is not necessarily 1
Then you still have to find out if there is 1 in the set where the element is located
Then rewrite the find function
The following is a section of code for counting the number. The rest of the code is very simple. Just copy it according to the template of query set
//Start traversing from two root nodes and count the number of nodes
//No, the root node is not necessarily 1. Find the root node of 1 and count the number of root nodes with the same number as the root node of 1
root=find(1,0);
for(int i=2;i<=N;i++)
{
int k=find(i,0);
if(k == root) cnt_1++;
}
root=find(1,1);//Because the absolute value function has been used, we start from 1 instead of - 1
for(int i=2;i<=M;i++)
{
int k=find(i,1);
if(k == root) cnt_2++;
}
if(cnt_1>cnt_2) cout<<cnt_2;
else cout<<cnt_1;
//The above is the content of the main function
//Here is the find function
int find(int x,int k)
{
int x_root=x;
while(parent[x_root][k]!=0)
{
x_root=parent[x_root][k];
}
return x_root;//Recursive root finding
}I didn't know what to think at the beginning. I changed it for more than four hours. People were stupid.
Write again next time when you think about it clearly. Don't make another compilation error. If you don't hand it in, delete, modify and change it again. When you come back after taking a bath, you have a clear idea. Write again. Although there are still some small problems, it's just a little change. Before I did it without thinking clearly, I was confused. If I missed this and that, I ignored many conditions and special circumstances and did not consider them comprehensively.
Ideas for future questions:
1. Figure out what method to use and what algorithms to use
2. From a strategically advantageous position and modular thinking, this is still used well. There are a lot of functions, and everything is not crowded into the main function
3. Pay attention to where, which details or the operating conditions of which topic. If the details are unclear, draw a picture! Drawing is really useful
4. Consider special circumstances
First time: unexpected 30
#include<iostream>
using namespace std;
#define MAX_TREE_SIZE 20010
int parent_1[MAX_TREE_SIZE]={0};
int deep_1[MAX_TREE_SIZE]={0};
int parent_2[MAX_TREE_SIZE]={0};
int deep_2[MAX_TREE_SIZE]={0};
int cnt_1=1,cnt_2=1;//At first, there were Xiao Ming and Xiao Hong
void initial(int n)
{
for(int i=0;i<n;i++)
{
parent_1[i]=0;
deep_1[i]=0;
parent_2[i]=0;
deep_2[i]=0;
}
}
int find_root_1(int x)
{
int x_root=x;
while(parent_1[x_root]!=0)
{
x_root=parent_1[x_root];
}
return x_root;
}
void combine_1(int x,int y)
{
int x_root=find_root_1(x);
int y_root=find_root_1(y);
if(x_root!=y_root)
{
if(deep_1[x_root]>deep_1[y_root])
{
parent_1[y_root]=x_root;
}
else if(deep_1[x_root]<deep_1[y_root])
{
parent_1[x_root]=y_root;
}
else
{
parent_1[x_root]=y_root;
deep_1[y_root]++;
}
}
cnt_1++;
}
int find_root_2(int x)
{
int x_root=x;
while(parent_2[x_root]!=0)
{
x_root=parent_2[x_root];
}
return x_root;
}
void combine_2(int x,int y)
{
int x_root=find_root_2(x);
int y_root=find_root_2(y);
if(x_root!=y_root)
{
if(deep_2[x_root]>deep_2[y_root])
{
parent_2[y_root]=x_root;
}
else if(deep_2[x_root]<deep_2[y_root])
{
parent_2[x_root]=y_root;
}
else
{
parent_2[x_root]=y_root;
deep_2[y_root]++;
}
cnt_2++;
}
}
int main()
{
int N,M,P,Q;//Company A has N employees, including P pairs of friends. Company B has M employees, including Q pairs of friends
cin>>N>>M>>P>>Q;
int x1,y1;
for(int i=0;i<P;i++)
{
cin>>x1>>y1;
combine_1(x1,y1);
}
int x2,y2;
for(int i=0;i<Q;i++)
{
cin>>x2>>y2;
combine_2(x2,y2);
}
if(cnt_1>cnt_2)
{
cout<<cnt_2;
}
else
{
cout<<cnt_1;
}
}Second time: unexpected 30
#include<iostream>
using namespace std;
#define MAX_TREE_SIZE 20010
int parent_1[MAX_TREE_SIZE]={0};
int deep_1[MAX_TREE_SIZE]={0};
int parent_2[MAX_TREE_SIZE]={0};
int deep_2[MAX_TREE_SIZE]={0};
int cnt_1=1,cnt_2=1;//At first, there were Xiao Ming and Xiao Hong
void initial(int n)
{
for(int i=0;i<n;i++)
{
parent_1[i]=0;
deep_1[i]=0;
parent_2[i]=0;
deep_2[i]=0;
}
}
int find_root_1(int x)
{
int x_root=x;
while(parent_1[x_root]!=0)
{
x_root=parent_1[x_root];
}
return x_root;
}
void check_1(int x,int y)
{
int x_root=find_root_1(x);
int y_root=find_root_1(y);
if(x_root!=y_root) cnt_1++;
}
void combine_1(int x,int y)
{
check_1(x,y);
//If you make friends, you can't directly + 1. Because a friend's friend is also a friend, you should first check whether they are in the same set
int x_root=find_root_1(x);
int y_root=find_root_1(y);
if(x_root!=y_root)
{
if(deep_1[x_root]>deep_1[y_root])
{
parent_1[y_root]=x_root;
}
else if(deep_1[x_root]<deep_1[y_root])
{
parent_1[x_root]=y_root;
}
else
{
parent_1[x_root]=y_root;
deep_1[y_root]++;
}
}
}
int find_root_2(int x)
{
int x_root=x;
while(parent_2[x_root]!=0)
{
x_root=parent_2[x_root];
}
return x_root;
}
void check_2(int x,int y)
{
int x_root=find_root_2(x);
int y_root=find_root_2(y);
if(x_root!=y_root) cnt_2++;
}
void combine_2(int x,int y)
{
check_2(x,y);
int x_root=find_root_2(x);
int y_root=find_root_2(y);
if(x_root!=y_root)
{
if(deep_2[x_root]>deep_2[y_root])
{
parent_2[y_root]=x_root;
}
else if(deep_2[x_root]<deep_2[y_root])
{
parent_2[x_root]=y_root;
}
else
{
parent_2[x_root]=y_root;
deep_2[y_root]++;
}
}
}
int main()
{
int N,M,P,Q;//Company A has N employees, including P pairs of friends. Company B has M employees, including Q pairs of friends
cin>>N>>M>>P>>Q;
int x1,y1;
for(int i=0;i<P;i++)
{
cin>>x1>>y1;
combine_1(x1,y1);
}
int x2,y2;
for(int i=0;i<Q;i++)
{
cin>>x2>>y2;
combine_2(x2,y2);
}
if(cnt_1>cnt_2)
{
cout<<cnt_2;
}
else
{
cout<<cnt_1;
}third time:
#include<iostream>
#include<cmath>
using namespace std;
#define MAX_TREE_SIZE 20010
int parent_1[MAX_TREE_SIZE]={0};
int deep_1[MAX_TREE_SIZE]={0};
int parent_2[MAX_TREE_SIZE]={0};
int deep_2[MAX_TREE_SIZE]={0};
int cnt_1=1,cnt_2=1;//At first, there were Xiao Ming and Xiao Hong
int checkkk=1;//Make sure Xiaoming and Xiaohong are in the collection
int x1_root,x2_root;//Root node of male female joint search set
void initial(int n)
{
for(int i=0;i<n;i++)
{
parent_1[i]=0;
deep_1[i]=0;
parent_2[i]=0;
deep_2[i]=0;
}
}
int find_root_1(int x)
{
int x_root=x;
while(parent_1[x_root]!=0)
{
x_root=parent_1[x_root];
}
return x_root;
}
void check_1(int x,int y)
{
int x_root=find_root_1(x);
int y_root=find_root_1(y);
if(x_root!=y_root) cnt_1++;
}
void combine_1(int x,int y)
{
check_1(x,y);
//If you make friends, you can't directly + 1. Because a friend's friend is also a friend, you should first check whether they are in the same set
int x_root=find_root_1(x);
int y_root=find_root_1(y);
if(x_root!=y_root)
{
if(deep_1[x_root]>deep_1[y_root])
{
parent_1[y_root]=x_root;
}
else if(deep_1[x_root]<deep_1[y_root])
{
parent_1[x_root]=y_root;
}
else
{
parent_1[x_root]=y_root;
deep_1[y_root]++;
}
}
x1_root=x_root;
}
int find_root_2(int x)
{
int x_root=x;
while(parent_2[x_root]!=0)
{
x_root=parent_2[x_root];
}
return x_root;
}
void check_2(int x,int y)
{
int x_root=find_root_2(x);
int y_root=find_root_2(y);
if(x_root!=y_root) cnt_2++;
}
void combine_2(int x,int y)
{
check_2(x,y);
int x_root=find_root_2(x);
int y_root=find_root_2(y);
if(x_root!=y_root)
{
if(deep_2[x_root]>deep_2[y_root])
{
parent_2[y_root]=x_root;
}
else if(deep_2[x_root]<deep_2[y_root])
{
parent_2[x_root]=y_root;
}
else
{
parent_2[x_root]=y_root;
deep_2[y_root]++;
}
}
x2_root=x_root;
}
void check(int xiaoming,int x1_root,int xiaohong,int x2_root)
{
int x_root,y_root;
x_root=find_root_1(xiaoming);
y_root=find_root_1(x1_root);
if(x_root!=y_root)
checkkk=0;
x_root=find_root_1(xiaohong);
y_root=find_root_1(x2_root);
if(x_root!=y_root)
checkkk=0;
}
int main()
{
int N,M,P,Q;
//Company A has N employees, including P pairs of friends
//Company B has M employees, including Q pairs of friends
cin>>N>>M>>P>>Q;
int x,y;
for(int i=0;i<P;i++)//Combine A company with P relationship
{
cin>>x>>y;
combine_1(x,y);
}
for(int i=0;i<Q;i++)//Combine company B with Q-pair relationship
{
cin>>x>>y;
combine_2(abs(x),abs(y));
}
check(1,x1_root,abs(-1),x2_root);//Check whether Xiaoming and Xiaohong are in the two groups. Xiaoming and Xiaohong act as a bridge
if(checkkk==1)
{
if(cnt_1>cnt_2)
{
cout<<cnt_2;
}
else
{
cout<<cnt_1;
}
}
else
{
cout<<"1";
}
}
AC Code:
#include<iostream>
#include<cmath>
using namespace std;
#define MAX_TREE_SIZE 20010
int parent[MAX_TREE_SIZE][2]={0};
int deep[MAX_TREE_SIZE]={0};
//Sort out the two parallel search sets first
int find_root_1(int x);
void combine_1(int x,int y);
int find_root_2(int x);
void combine_2(int x,int y);
int find(int x,int k);
int cnt_1=1,cnt_2=1,root;//Xiao Ming and Xiao Hong are known to have at least one pair
int main()
{
int N,M,P,Q;
//Company A has N employees, including P pairs of friends
//Company B has M employees, including Q pairs of friends
cin>>N>>M>>P>>Q;
int x,y;
void initial_1(int n);
for(int i=0;i<P;i++)//Combine A company with P relationship
{
cin>>x>>y;
combine_1(x,y);
}
void initial_2(int n);
for(int i=0;i<Q;i++)//Combine company B with Q-pair relationship
{
cin>>x>>y;
combine_2(abs(x),abs(y));
}
//Start traversing from two root nodes and count the number of nodes
//No, the root node is not necessarily 1. Find the root node of 1 and count the number of root nodes with the same number as the root node of 1
root=find(1,0);
for(int i=2;i<=N;i++)
{
int k=find(i,0);
if(k == root) cnt_1++;
}
root=find(1,1);//Because the absolute value function has been used, we start from 1 instead of - 1
for(int i=2;i<=M;i++)
{
int k=find(i,1);
if(k == root) cnt_2++;
}
if(cnt_1>cnt_2) cout<<cnt_2;
else cout<<cnt_1;
}
int find(int x,int k)
{
int x_root=x;
while(parent[x_root][k]!=0)
{
x_root=parent[x_root][k];
}
return x_root;//Recursive root finding
}
void initial_1(int n)
{
for(int i=0;i<n;i++)
{
parent[i][0]=0;
deep[i]=0;
}
}
int find_root_1(int x)
{
int x_root=x;
while(parent[x_root][0]!=0)
{
x_root=parent[x_root][0];
}
return x_root;
}
void combine_1(int x,int y)
{
int x_root=find_root_1(x);
int y_root=find_root_1(y);
if(x_root!=y_root)
{
if(deep[x_root]>deep[y_root])
{
parent[y_root][0]=x_root;
}
else if(deep[x_root]<deep[y_root])
{
parent[x_root][0]=y_root;
}
else
{
parent[x_root][0]=y_root;
deep[y_root]++;
}
}
}
void initial_2(int n)
{
for(int i=0;i<n;i++)
{
parent[i][1]=0;
deep[i]=0;
}
}
int find_root_2(int x)
{
int x_root=x;
while(parent[x_root][1]!=0)
{
x_root=parent[x_root][1];
}
return x_root;
}
void combine_2(int x,int y)
{
int x_root=find_root_2(x);
int y_root=find_root_2(y);
if(x_root!=y_root)
{
if(deep[x_root]>deep[y_root])
{
parent[y_root][1]=x_root;
}
else if(deep[x_root]<deep[y_root])
{
parent[x_root][1]=y_root;
}
else
{
parent[x_root][1]=y_root;
deep[y_root]++;
}
}
}