1. Concept understanding
1.1 mathematical basis
Very boring, do not want to see can not see.
1.1.1 Bayesian probability
1.1.1.1 conditional probability
Naive Bayesian classification algorithm is a classification method based on Bayesian theorem and the assumption of independence of feature conditions. Therefore, if you want to understand the algorithm principle behind naive Bayesian classification algorithm, you have to use some knowledge of probability theory, the first is conditional probability. Next, let's start our journey of conditional probability.
1.1.1.2 what is conditional probability
Probability refers to the possibility of an event A, expressed as P(A). The conditional probability refers to the possibility of another event B under the condition that one event A has occurred, expressed as P(B|A), for example:
There is a 25% chance of rain today, that is, P (rain) = 0.25;
Today, 75% of the probability is sunny, that is, P (sunny) = 0.75;
If it rains, I have a 75% chance to wear a coat, that is, P (wear a coat | rain) = 0.75;
If it rains, I have a 25% chance to wear a T-shirt, that is, P (wear a T-shirt | rain) = 0.25;
As can be seen from the above example, the conditional probability describes the possibility of the event on the left after the event on the right has occurred, rather than the possibility of two events happening at the same time!
1.1.1.3 how to calculate conditional probability
Suppose A and B are two events, and P (A) > 0, P(B|A)=P(AB)/P(A) is the conditional probability of event B under the condition that event A occurs. (where P(AB) represents the probability of simultaneous occurrence of event A and event B)
For example, there is a table that counts the quantity of qualified products and defective products in the products produced by factory a and factory B. The data are as follows:
| Factory a | Factory B | total | |
|---|---|---|---|
| Qualified products | 475 | 644 | 1119 |
| Defective products | 25 | 56 | 81 |
| total | 500 | 700 | 1200 |
Now we want to calculate the probability that the known products are produced by factory a. At this time, we are actually calculating the conditional probability. The calculation is very simple.
Suppose event A means that the product is produced by factory A and event B means that the product is defective. According to the data in the table, P(AB)=25/1200, P(A)=500/1200. Then P(B|A)=P(AB)/P(A)=25/500.
1.1.1.4 multiplication theorem
Multiplying both sides of the formula of conditional probability by P(A) at the same time becomes the multiplication theorem, that is, P(AB)=P(B|A)*P(A). So how to use the multiplication theorem? for instance:
At present, there are 100 products in a batch and 10 defective products. Take one product each time without putting it back. Now I want to calculate the probability that the first time is defective and the second time is genuine.
From the point of view of the question, this question asks the probability that the first time is a defective product and the second time is a genuine product. So we can use multiplication theorem to solve this problem.
Suppose event A is defective for the first time and event B is genuine for the second time. Then P(AB)=P(A)P(B|A)=(10/100)(90/99)=0.091.
1.1.1.5 some calculation problems
1. P(AB) represents the probability that event A and event B occur at the same time, and P(A|B) represents the probability that event A occurs under the condition that event B has occurred.
A. Right
B. Wrong
2. From 1, 2,..., 15, Xiaoming and Xiaohong take a number respectively. Now it is known that Xiaoming takes a multiple of 5. What is the probability that Xiaoming takes a number greater than Xiaohong?
A,7/14
B,8/14
C,9/14
D,10/14
1.1.2 full probability formula
Bayesian formula is the core mathematical theory of naive Bayesian classification algorithm. Before understanding Bayesian formula, we need to understand the relevant knowledge of full probability formula.
1.1.2.1 cited examples
There are three direct routes from Xiaoming's home to the company, as shown in the figure below:
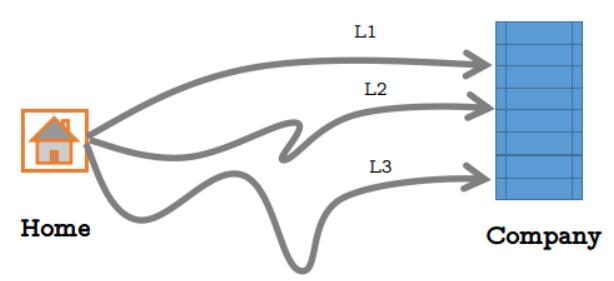
However, the possibility of daily congestion on each road is different. Due to the different distance of the road, the probability of selecting each road is as follows:
L1: 0.5 ;L2: 0.3 ;L3: 0.2.
The probability of no traffic jam when going to the company from the above three roads every day is as follows:
L1 no traffic jam: 0.2; L2 no traffic jam: 0.4; L3 no traffic jam: 0.7.
If there is no traffic jam, he will not be late. Now Xiao Ming wants to calculate the probability that he will not be late for work. What should he do?
In fact, it is very simple. Suppose event C is that Xiao Ming is not late, event A1 is that Xiao Ming chooses L1 and there is no traffic jam, event A2 is that Xiao Ming chooses L2 and there is no traffic jam, and event A3 is that Xiao Ming chooses L3 and there is no traffic jam. So obviously P ©= P(A1)+P(A2)+P(A3).
So the question is, how do P(A1), P(A2) and P(A3) count? In fact, as long as you can calculate P(A1), you can calculate everything else. We can also assume that event D1 is Xiaoming's choice of route L1 and event E1 is no traffic jam. Then P(A1)=P(D1)*P(E1). But from the table, we only know that P(D1)=0.5. What should we do?
Recall the multiplication theorem introduced in the previous level. It is not difficult to think of P(A1)=P(D1)P(E1|D1). It can be seen from the table that P(E1|D1)=0.2. So P(A1)=0.50.2=0.1.
Then we can quickly calculate that P(A2)=0.30.4=0.12, P(A3)=0.20.7=0.14. So p ©= 0.1+0.12+0.14=0.36.
1.1.2.2 full probability formula
When there are many ways to achieve a certain goal, if you want to know the probability of achieving the goal through all ways, you need to use the full probability formula (this is the case in the above example!). The full probability formula is defined as follows:
If events B1, B2,..., Bn are incompatible with each other, and their probability sum is 1. Then for any event, C satisfies:

In the cited example, the probability of which path Xiaoming chooses to go to the company is mutually incompatible (only one path can be selected to go to the company), and the sum is 1. Therefore, the probability that Xiao Ming will not be late can be calculated by the full probability formula, and the calculation process in the cited example is the full probability formula.
1.1.3 Bayesian formula
When we know the probability of various causes causing the event and want to calculate the probability of the event, we can use the full probability formula. However, if we want to calculate the probability of various causes of the event, we need to use Bayesian formula.
The Bayesian formula is defined as follows, where A represents the event that has occurred, and Bi is the ith cause of event A:
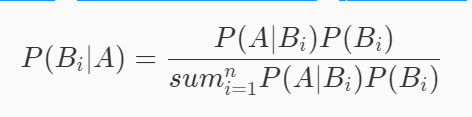
Bayesian formula looks complex, but it is actually very simple. The numerator part is the multiplication theorem and the denominator part is the full probability formula (the denominator is equal to P(A)).
If we make a simple mathematical transformation of the Bayesian formula (multiply both sides by the denominator and divide both sides by P(Bi)). The following formula can be obtained:
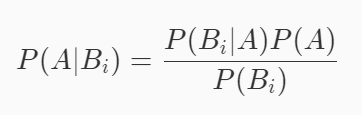
This formula is the core mathematical formula of naive Bayesian classification algorithm.
1.1.3.1 multiple choice questions
1. The results of previous data analysis show that when the machine is well adjusted, the qualified rate of the product is 98%, and when the machine has some fault, the qualified rate of the product is 55%. When the machine starts every morning, the probability of good adjustment of the machine is 95%. Calculate the probability that the machine will adjust well when the first product is qualified in the morning?
A,0.94
B,0.95
C,0.96
D,0.97
2. There are 8 products in a batch, including 6 genuine products and 2 defective products. Now take the product from it twice without putting it back, one at a time, and find the probability of obtaining genuine products for the second time.
A,1/4
B,1/2
C,3/4
D,1
2. Example analysis
2.1 good melons and bad melons are watermelons
In the hot summer, you may need to buy a big watermelon to relieve the heat, but although your experience in picking watermelon is very old, there will still be times when you pick the wrong one. Nevertheless, you may prefer to believe in your experience. Suppose there is a clear grain in front of you and the sound is thick after patting the watermelon. According to your experience, the probability that the watermelon is a good melon is 80%, and the probability that it is not a good melon is 20%. Then at this time, you will subconsciously think that this watermelon is a good melon, because the probability that it is a good melon is greater than the probability that it is not a good melon.
2.1.1 prediction process of naive Bayesian classification algorithm
The prediction idea of naive Bayesian classification algorithm is the same as the idea of picking watermelon in the cited example. It will calculate the probability that the data to be predicted are all categories according to previous experience, and then select the category with the highest probability as the classification result.
The data of a watermelon is shown in the following table:
| colour | voice | texture | Is it a good melon |
|---|---|---|---|
| green | Crisp | clear | ? |
If we want to use the idea of naive Bayesian classification algorithm to infer whether the watermelon is a good melon according to the three characteristics of color, sound and texture in the data, we need to calculate the probability that the watermelon is a good melon and the probability that it is not a good melon.
Assuming that event A1 is a good melon, event B is green, event C is crisp and event D is clear, the probability that this watermelon is a good melon is P(A1|BCD). According to the formula mentioned at the end of the previous level:
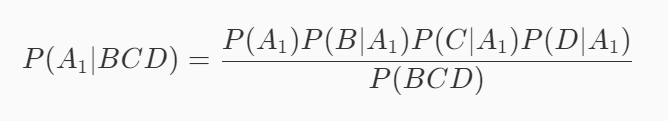
Similarly, assuming that event A2 is not a good melon, event B is green, event C is crisp and event D is clear, the probability that this watermelon is not a good melon is P(A2|BCD). According to the formula mentioned at the end of the previous level:
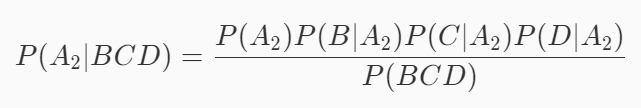
The idea of naive Bayesian classification algorithm is to take the category with the greatest probability as the prediction result. Therefore, if the following formula is satisfied, it is considered that this watermelon is a good melon, otherwise it is not a good melon:
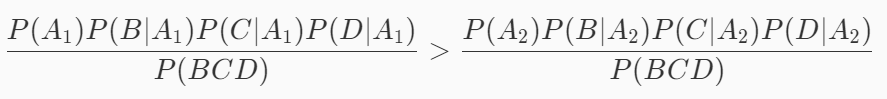
It can be seen from the above formula that the number of P(BCD) has no effect on judging which category has a high probability, so the formula can be simplified into the following form:
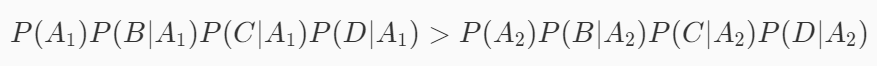
Therefore, in prediction, we need to know how much P(A1), P(A2), P(B|A_1), P(C|A_1) and P(D|A_1) are equal. These probabilities can be calculated in the training stage.
2.1.2 training process of naive Bayesian classification algorithm
The training process is very simple, mainly calculating various conditional probabilities. Suppose there is a set of watermelon data, as shown in the following table:
| number | colour | voice | texture | Is it a good melon |
|---|---|---|---|---|
| 1 | green | Crisp | clear | yes |
| 2 | yellow | Thick | vague | no |
| 3 | green | Thick | vague | yes |
| 4 | green | Crisp | clear | yes |
| 5 | yellow | Thick | vague | yes |
| 6 | green | Crisp | clear | no |
As can be seen from the data in the table:
P (good melon) = 4 / 6,
P (color green | good melon) = 3 / 4,
P (color yellow | good melon) = 1 / 4,
P (crisp sound | good melon) = 1 / 2,
P (thick voice is a good melon) = 1 / 2,
P (clear texture | good melon) = 1 / 2,
P (texture blur | good melon) = 1 / 2,
P (not a good melon) = 2 / 6,
P (color green | not good melon) = 1 / 2,
P (color yellow | good melon) = 1 / 2,
P (crisp sound | not good melon) = 1 / 2,
P (thick voice is not a good melon) = 1 / 2,
P (clear texture | not good melon) = 1 / 2,
P (texture blur | not good) = 1 / 2.
When the above probability is obtained, the task of the training stage has been completed. We might as well go back and predict whether this watermelon is a good one.
| colour | voice | texture | Is it a good melon |
|---|---|---|---|
| green | Crisp | clear | ? |
Suppose event A1 is good melon, event B is green, event C is crisp and event D is clear. Then there are:
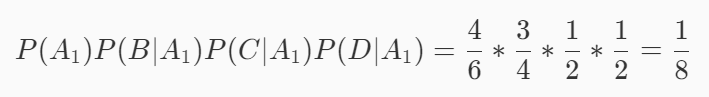
Suppose event A2 is not good, event B is green, event C is crisp, and event D is clear. Then there are:
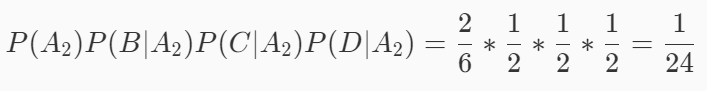
Because 1 / 8 > 1 / 24, this watermelon is a good melon.
2.2 both good and bad watermelons should be smooth
Laplace smoothing
Assuming that there is such a batch of watermelon data, you should be able to quickly know how to train the model according to the knowledge mentioned in the previous level.
| number | colour | voice | texture | Is it a good melon |
|---|---|---|---|---|
| 1 | green | Crisp | clear | yes |
| 2 | yellow | Thick | clear | no |
| 3 | green | Thick | vague | yes |
| 4 | green | Crisp | clear | yes |
| 5 | yellow | Thick | vague | yes |
| 6 | green | Crisp | clear | no |
However, it should be noted that among the data that are not good melons, no texture is fuzzy, that is, P (fuzzy | no) = 0. Obviously, if no processing is done, when predicting, as long as the texture value in the prediction data is fuzzy, the probability that the model predicts that it is not a good melon must be 0 (the probability is continuous multiplication, and as long as one item is 0, the result is 0). This is obviously unreasonable, so we need to smooth, and the most commonly used method is Laplace smoothing.
Laplace smoothing refers to the assumption that n represents the total number of categories in the training data set, and Ni represents the total number of values in column i of the training data set. In the training process, when calculating the probability of category, the numerator is added with 1, the denominator is added with N, and when calculating the conditional probability, the numerator is added with 1 and the denominator is added with Ni.
Next, use the above watermelon data to simulate it. You can know from the table
N=2,N1=2,N2=2,N3=2.
P (good melon) = (4 + 1) / (6 + 2),
P (color green | good melon) = (3 + 1) / (4 + 2),
P (color yellow | good melon) = (1 + 1) / (4 + 2),
P (crisp sound | good melon) = (1 + 1) / (2 + 2),
P (thick voice | good melon) = (1 + 1) / (2 + 2),
P (clear texture | good melon) = (1 + 1) / (2 + 2),
P (texture blur | good melon) = (1 + 1) / (2 + 2),
P (not a good melon) = (2 + 1) / (6 + 2),
P (color green | not good melon) = (1 + 1) / (2 + 2),
P (color yellow | good melon) = (1 + 1) / (2 + 2),
P (crisp sound | not a good melon) = (1 + 1) / (2 + 2),
P (thick voice | not a good melon) = (1 + 1) / (2 + 2),
P (clear texture | not a good melon) = (1 + 1) / (2 + 2),
P (texture blur | not good) = (0 + 1) / (2 + 2).
It can be seen that after Laplace smoothing, P (fuzzy | no) is smoothed to 1 / 4, making the model more reasonable.
2.3 topic classification of news text
You need to master how to use the MultinomialNB class and text vectorization provided by sklearn.
2.3.1 data introduction
The 20 newsgroups data set is used in this study. The 20 newsgroups data set is one of the international standard data sets for text classification, text mining and information retrieval. The data set collected 18846 newsgroup documents, which were evenly divided into 20 newsgroup collections with different topics (such as computer hardware, the Middle East, etc.).
Some data are as follows:
From: Mamatha Devineni Ratnam <mr47+@andrew.cmu.edu> Subject: Pens fans reactions Organization: Post Office, Carnegie Mellon, Pittsburgh, PA Lines: 12 NNTP-Posting-Host: po4.andrew.cmu.edu I am sure some bashers of Pens fans are pretty confused about the lack of any kind of posts about the recent Pens massacre of the Devils. Actually, I am bit puzzled too and a bit relieved. However, I am going to put an end to non-PIttsburghers relief with a bit of praise for the Pens. Man, they are killing those Devils worse than I thought. Jagr just showed you why he is much better than his regular season stats. He is also a lot fo fun to watch in the playoffs. Bowman should let JAgr have a lot of fun in the next couple of games since the Pens are going to beat the pulp out of Jersey anyway. I was very disappointed not to see the Islanders lose the final regular season game. PENS RULE!!!
The topic tag corresponding to the news text has been represented by 20 numbers 0-19.
2.3.2 text Vectorization
Since each piece of data in the dataset is a very long string, we need to vectorize the data. For example, I have a apple! I have a pen! You may need to convert the string into a vector, such as [10, 7, 0, 1, 2, 6, 22, 100, 8, 0, 1, 0].
sklearn provides the CountVectorizer class to realize the word frequency vectorization function. To vectorize the data, the code is as follows:
from sklearn.feature_ext\fraction.text import CountVectorizer #Instantiate vectorized objects vec = CountVectorizer() #Vectorize the news in the training set X_train = vec.fit_transform(X_train) #Vectorize the news in the test set X_test = vec.transform(X_test)
However, there is a problem in converting text into vectors only by counting word frequency: long articles will appear more times than short articles, and in fact, both articles may talk about the same topic.
To solve this problem, we can use TF IDF to build text vectors. The TF IDF interface has been provided in sklearn. The example code is as follows:
from sklearn.feature_ext\fraction.text import TfidfTransformer #Instantiate TF IDF object tfidf = TfidfTransformer() #The word frequency vector in the training set is transformed with TF IDF X_train = tfidf.fit_transform(X_train_count_vectorizer) #The word frequency vector in the test set is converted with TF IDF X_test = vec.transform(X_test_count_vectorizer)
2.3.3 MultinomialNB
MultinomialNB is the implementation of naive Bayesian algorithm for multinomial distributed data in sklearn, and it is a classical naive Bayesian algorithm for text classification. It is recommended to use MultinomialNB to realize the text classification function in this level.
alpha is a common parameter when MultinomialNB is instantiated.
- alpha: smoothing factor.
- When equal to 1, Laplace smoothing is done;
- When it is less than 1, Lidstone smoothing is used;
- When equal to 0, no smoothing is done.
The fit function in MultinomialNB class realizes the function of training model of naive Bayesian classification algorithm, and the predict function realizes the function of model prediction.
The parameters of fit function are as follows:
- 10: Darry with the size of [number of samples, number of features] stores training samples
- Y: The value is integer and the size is [number of samples] ndarray, which stores the classification label of training samples
The predict function has a vector input:
- 10: The ndarry with the size of [number of samples, number of features] stores prediction samples
The usage code of MultinomialNB is as follows:
clf = MultinomialNB() clf.fit(X_train, Y_train) result = clf.predict(X_test)
3. Code example
3.1 good melons and bad melons are watermelons
3.1.1 programming requirements
According to the prompt, the fit and predict functions are completed to realize the training and prediction of the model respectively. (PS: in the fit function, you need to save the probability required for prediction into two variables: self.label_prob and self.condition_prob)
The fit function parameters are explained as follows:
- feature: training set data, type: ndarray;
- Label: training set label, type: ndarray;
- Return: no return.
The parameters of the predict function are explained as follows:
- Feature: ndarray composed of all features of the test dataset. (PS: there are multiple pieces of data in the feature);
- Return: the result predicted by the model. (PS: you need to return a list or ndarry of any length according to the number of pieces of data in the feature.).
3.1.2 test description
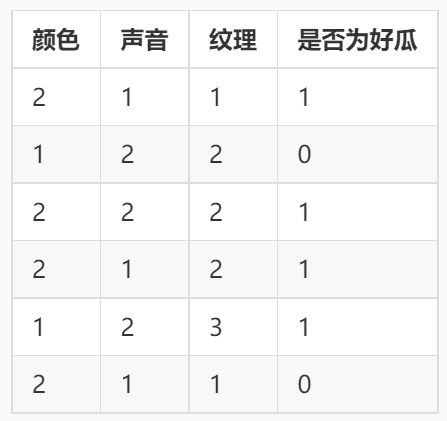
Some training data are as follows
(PS: the data is stored in the way of ndarray, excluding the header. The color column is 1 for green and 2 for yellow; the sound column is 1 for crisp and 2 for thick. The texture column is 1 for clear, 2 for fuzzy and 3 for general):
3.1.3 actual code
import numpy as np
class NaiveBayesClassifier(object):
def __init__(self):
'''
self.label_prob Represents the probability that each category appears in the data
For example,{0:0.333, 1:0.667}Indicates that the probability of occurrence of category 0 in the data is 0.333,The probability of category 1 is 0.667
'''
self.label_prob = {}
'''
self.condition_prob Represents the probability of occurrence of each feature under the conditions determined by each category
For example, the characteristics of the training dataset are [[2, 1, 1],
[1, 2, 2],
[2, 2, 2],
[2, 1, 2],
[1, 2, 3]]
Label is[1, 0, 1, 0, 1]
Then when the tag is 0, the probability that the value of column 0 is 1 is 0.5,The probability of a value of 2 is 0.5;
When the tag is 0, the probability that the value of column 1 is 1 is 0.5,The probability of a value of 2 is 0.5;
When the tag is 0, the probability that the value in column 2 is 1 is 0, the probability that the value is 2 is 1, and the probability that the value is 3 is 0;
When the tag is 1, the probability that the value of column 0 is 1 is 0.333,The probability of a value of 2 is 0.666;
When the tag is 1, the probability that the value of column 1 is 1 is 0.333,The probability of a value of 2 is 0.666;
When the tag is 1, the probability that the value of column 2 is 1 is 0.333,The probability of a value of 2 is 0.333,The probability of a value of 3 is 0.333;
therefore self.label_prob The values are as follows:
{
0:{
0:{
1:0.5
2:0.5
}
1:{
1:0.5
2:0.5
}
2:{
1:0
2:1
3:0
}
}
1:
{
0:{
1:0.333
2:0.666
}
1:{
1:0.333
2:0.666
}
2:{
1:0.333
2:0.333
3:0.333
}
}
}
'''
self.condition_prob = {}
def fit(self, feature, label):
'''
To train the model, various probabilities need to be saved in self.label_prob and self.condition_prob in
:param feature: The training dataset consists of all features ndarray
:param label:The training dataset consists of all tags ndarray
:return: No return
'''
#********* Begin *********#
row_num = len(feature)
col_num = len(feature[0])
for c in label:# Number of occurrences per category
if c in self.label_prob:
self.label_prob[c] += 1
else:
self.label_prob[c] = 1
for key in self.label_prob.keys():
# Calculate the probability of each category in the dataset
self.label_prob[key] /= row_num
# Build self.condition_ The key in prob initializes each brace
self.condition_prob[key] = {}# The second brace of the dictionary set above, category 01
for i in range(col_num):
self.condition_prob[key][i] = {}# Third brace
for k in np.unique(feature[:, i], axis=0):# axis=0, see 5. [1]
self.condition_prob[key][i][k] = 0# Conditional probabilities of different characteristics in the third brace
# Record the feature, which element is in each group of the feature, and put it into the corresponding condition_ Where is the prob and record the number
for i in range(len(feature)):
for j in range(len(feature[i])):
if feature[i][j] in self.condition_prob[label[i]]:
self.condition_prob[label[i]][j][feature[i][j]] += 1
else:
self.condition_prob[label[i]][j][feature[i][j]] = 1
# Divide by the total number to get each probability
for label_key in self.condition_prob.keys():
for k in self.condition_prob[label_key].keys():
total = 0
for v in self.condition_prob[label_key][k].values():
total += v
for kk in self.condition_prob[label_key][k].keys():
#Calculate the probability of each feature under the conditions determined by each category
self.condition_prob[label_key][k][kk] /= total
#********* End *********#
def predict(self, feature):
'''
Predict the data and return the prediction results
:param feature:The test data set consists of all features ndarray
:return:
'''
# ********* Begin *********#
result = []
#Each test data is predicted
for i, f in enumerate(feature):# See 5. [4] to traverse each data array
#Probability of possible categories
prob = np.zeros(len(self.label_prob.keys()))
ii = 0
for label, label_prob in self.label_prob.items():
#Calculation probability
prob[ii] = label_prob
for j in range(len(feature[0])):
prob[ii] *= self.condition_prob[label][j][f[j]]
ii += 1
#Take the category with the highest probability as the result
result.append(list(self.label_prob.keys())[np.argmax(prob)])# See 5. [5]
return np.array(result)
#********* End *********#
Second
import numpy as np
class NaiveBayesClassifier(object):
def __init__(self):
self.label_prob = {}
self.condition_prob = {}
def fit(self, feature, label):
#********* Begin *********#
feature0_index=np.where(label==0)
feature1_index=np.where(label==1)
feature0=feature[feature0_index]
feature1=feature[feature1_index]
self.label_prob[0]=len(feature0)/len(feature)
self.label_prob[1]=len(feature1)/len(feature)
sum0={}
for f0 in feature0:
for i in range(len(f0)):
if i in sum0:
sum0[i][f0[i]] = sum0[i].get(f0[i], 0) + 1 / len(feature0)
else:
sum0[i] = {}
sum0[i][f0[i]] = sum0[i].get(f0[i], 0) + 1 / len(feature0)
sum1={}
for f1 in feature1:
for i in range(len(f1)):
if i in sum1:
sum1[i][f1[i]] = sum1[i].get(f1[i], 0) + 1 / len(feature1)
else:
sum1[i] = {}
sum1[i][f1[i]] = sum1[i].get(f1[i], 0) + 1 / len(feature1)
self.condition_prob[0]=sum0;
self.condition_prob[1]=sum1;
#********* End *********#
def predict(self, feature):
# ********* Begin *********#
result=[]
for f in feature:
result1=self.label_prob[1]
result0=self.label_prob[0]
for i in range(len(f)):
result0*=self.condition_prob[0][i].get(f[i],0)
result1*=self.condition_prob[1][i].get(f[i],0)
if result0>result1:
result.append(0)
else:
result.append(1)
return np.array(result)
#********* End *********#
3.2 both good and bad watermelons should be smooth
The programming requirements and test instructions are the same as those in 3.1 and will not be repeated
3.2.1 code example
First kind
import numpy as np
class NaiveBayesClassifier(object):
def __init__(self):
self.label_prob = {}
self.condition_prob = {}
def fit(self, feature, label):
#********* Begin *********#
row_num = len(feature)
col_num = len(feature[0])
unique_label_count = len(set(label)) # See 5. [7]
for c in label:
if c in self.label_prob:
self.label_prob[c] += 1
else:
self.label_prob[c] = 1
for key in self.label_prob.keys():
# Calculate the probability of each category in the data set, Laplace smoothing
self.label_prob[key] += 1
self.label_prob[key] /= (unique_label_count+row_num) # Category count plus because it is Laplacian smoothing
# Build self.condition_ key in prob
self.condition_prob[key] = {}
for i in range(col_num):
self.condition_prob[key][i] = {}
for k in np.unique(feature[:, i], axis=0):
self.condition_prob[key][i][k] = 1
for i in range(len(feature)):
for j in range(len(feature[i])):
if feature[i][j] in self.condition_prob[label[i]]:
self.condition_prob[label[i]][j][feature[i][j]] += 1
for label_key in self.condition_prob.keys():
for k in self.condition_prob[label_key].keys():
#Laplace smoothing, different from the previous total=0, first assign him the number of categories of this category
total = len(self.condition_prob[label_key].keys())
for v in self.condition_prob[label_key][k].values():
total += v
for kk in self.condition_prob[label_key][k].keys():
# Calculate the probability of each feature under the conditions determined by each category
self.condition_prob[label_key][k][kk] /= total
#********* End *********#
def predict(self, feature):
result = []
# Each test data is predicted
for i, f in enumerate(feature):
# Probability of possible categories
prob = np.zeros(len(self.label_prob.keys()))
ii = 0
for label, label_prob in self.label_prob.items():
# Calculation probability
prob[ii] = label_prob
for j in range(len(feature[0])):
prob[ii] *= self.condition_prob[label][j][f[j]]
ii += 1
# Take the category with the highest probability as the result
result.append(list(self.label_prob.keys())[np.argmax(prob)])
return np.array(result)
Second
import numpy as np
class NaiveBayesClassifier(object):
def __init__(self):
self.label_prob = {}
self.condition_prob = {}
def fit(self, feature, label):
#********* Begin *********#
row_num = len(feature)
col_num = len(feature[0])
unique_label_count = len(set(label))
for c in label:
if c in self.label_prob:
self.label_prob[c] += 1
else:
self.label_prob[c] = 1
for key in self.label_prob.keys():
# Calculate the probability of each category in the data set, Laplace smoothing
self.label_prob[key] += 1
self.label_prob[key] /= (unique_label_count+row_num)
# Build self.condition_ key in prob
self.condition_prob[key] = {}
for i in range(col_num):
self.condition_prob[key][i] = {}
for k in np.unique(feature[:, i], axis=0):
self.condition_prob[key][i][k] = 1
for i in range(len(feature)):
for j in range(len(feature[i])):
if feature[i][j] in self.condition_prob[label[i]]:
self.condition_prob[label[i]][j][feature[i][j]] += 1
for label_key in self.condition_prob.keys():
for k in self.condition_prob[label_key].keys():
#Laplace smoothing
total = len(self.condition_prob[label_key].keys())
for v in self.condition_prob[label_key][k].values():
total += v
for kk in self.condition_prob[label_key][k].keys():
# Calculate the probability of each feature under the conditions determined by each category
self.condition_prob[label_key][k][kk] /= total
#********* End *********#
def predict(self, feature):
result = []
# Each test data is predicted
for i, f in enumerate(feature):
# Probability of possible categories
prob = np.zeros(len(self.label_prob.keys()))
ii = 0
for label, label_prob in self.label_prob.items():
# Calculation probability
prob[ii] = label_prob
for j in range(len(feature[0])):
prob[ii] *= self.condition_prob[label][j][f[j]]
ii += 1
# Take the category with the highest probability as the result
result.append(list(self.label_prob.keys())[np.argmax(prob)])
return np.array(result)
3.3 topic classification of news text
3.3.1 programming requirements
Fill in news_ The predict (train_sample, train_label, test_sample) function completes the task of news text topic classification, where:
- train_sample: original training sample, type: ndarray;
- train_label: training label, type: ndarray;
- test_sample: the original test sample with the type of ndarray.
3.3.2 test description
Just return the prediction results. Your code will be detected internally. If the prediction accuracy is higher than 0.8, it will be regarded as passing the test.
3.3.3 code example
from sklearn.feature_extraction.text import CountVectorizer # From sklearn.feature_ Import text feature vectorization module in extraction.text
from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import TfidfTransformer
def news_predict(train_sample, train_label, test_sample):
'''
Train the model and make prediction, and return the prediction results
:param train_sample:The news text in the original training set is of type ndarray
:param train_label:The topic tag corresponding to the news text in the training set. The type is ndarray
:test_sample:The news text in the original test set is of type ndarray
'''
# ********* Begin *********#
vec = CountVectorizer()
train_sample = vec.fit_transform(train_sample)
test_sample = vec.transform(test_sample)
tfidf = TfidfTransformer()
train_sample = tfidf.fit_transform(train_sample)
test_sample = tfidf.transform(test_sample)
mnb = MultinomialNB(alpha=0.01) # Initialize naive Bayes with default configuration
mnb.fit(train_sample, train_label) # The training data are used to estimate the model parameters
predict = mnb.predict(test_sample) # Predict parameters
return predict
# ********* End *********#
Second
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import TfidfTransformer
def news_predict(train_sample, train_label, test_sample):
vec = CountVectorizer()
X_train = vec.fit_transform(train_sample)
X_test = vec.transform(test_sample)
tfidf=TfidfTransformer()
X_train = tfidf.fit_transform(X_train)
X_test=tfidf.transform(X_test)
clf = MultinomialNB(alpha = 0.01)
clf.fit(X_train, train_label)
result = clf.predict(X_test)
return result
4. Application examples
4.1 spam filtering
Bayesian classifier is often used to filter spam. At this time, the feature of training data is the mail content itself, and there are only two categories of category labels, that is, spam or not spam.
The meaning of naive Bayesian hypothesis is that each word in the email content is conditionally independent when it is known whether the email is spam or not. Obviously, this assumption is actually not tenable, because when writing e-mail, we don't choose words from the thesaurus independently to form sentences, but organize words according to the relevance of the context.
Although naive Bayes hypothesis is against reality, it still has good results in practice with naive Bayes method.
5. Python learning
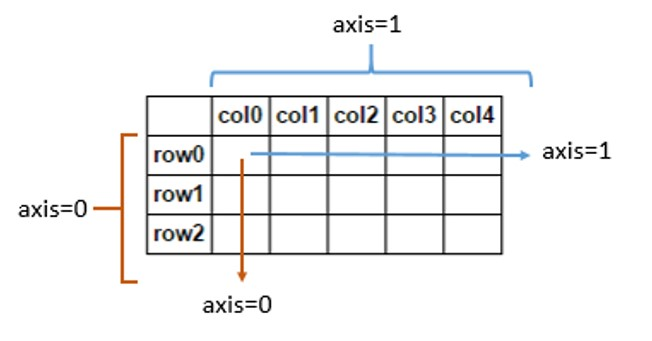
[1] axis=0 means down, and axis=1 means across
- A value of 0 means that the method is executed down the label \ index value of each column or row
- A value of 1 indicates that the corresponding method is executed along the label direction of each row or column
The following figure represents the meaning when axis is 0 and 1 in DataFrame:
[2] The numpy.unique function removes duplicate elements from the array.
[3] list indices must be integers or slices, not tuple solution:
Use the array in numpy to convert it into tuple: dataSet=np.array(dataSet)
Or convert the dataSet into a matrix: mat(dataSet)
[4] The enumerate () function is used to combine a traversable data object (such as list, tuple or string) into an index sequence, and list the data and data subscripts at the same time. It is generally used in the for loop
[5] The argmax function returns the index of the largest element along a given axis.
[6] numpy.zeros creates an array of the specified size, and the array elements are filled with 0:
[7] set()
>>>a = [1,2,3,4,5,6]
>>>print(len(set(a)))
6
>>>print(set(a))
{1, 2, 3, 4, 5, 6}