Machine learning algorithm series - Pocket Algorithm

Posted by wild_dog on Wed, 05 Jan 2022 10:08:52 +0100

Background knowledge required for reading this article: perceptron learning algorithm and yidui programming knowledge

1, Introduction

in the previous section, we learned the machine learning algorithm series (I) - perceptron learning algorithm (PLA), which can perfectly divide the data set into two types, but one prerequisite is that the data set is assumed to be linearly separable.

in the actual data collection process, there may be wrong data in the data set due to various reasons (for example, the mail word collected in the anti spam example is wrong or manual classification error, and the mail that is not spam is mistaken for spam). At this time, the data set may not be linearly separable, There is no way for perceptron learning algorithm to stop, so people have designed an algorithm based on perceptron learning algorithm, Pocket Algorithm, which can deal with linear indivisibility

Two, model introduction

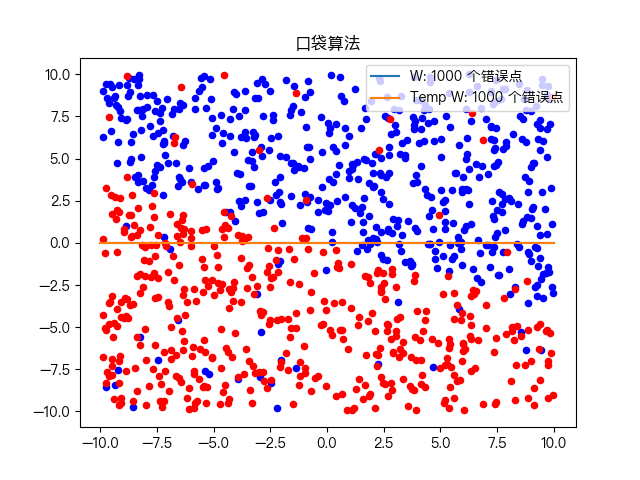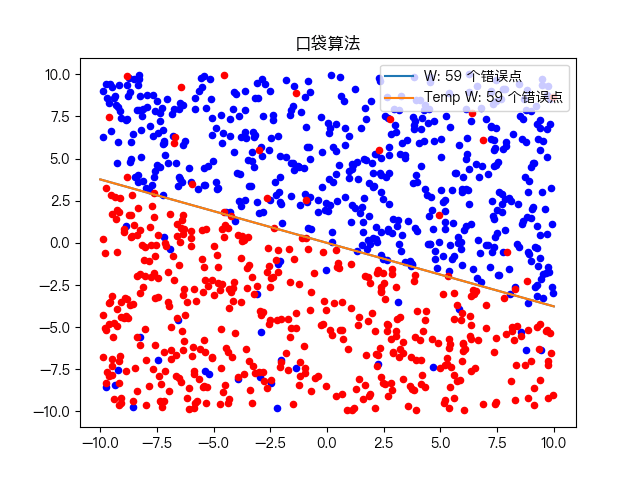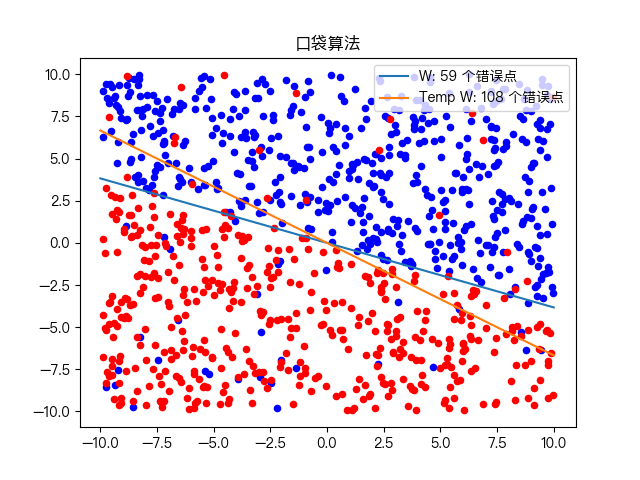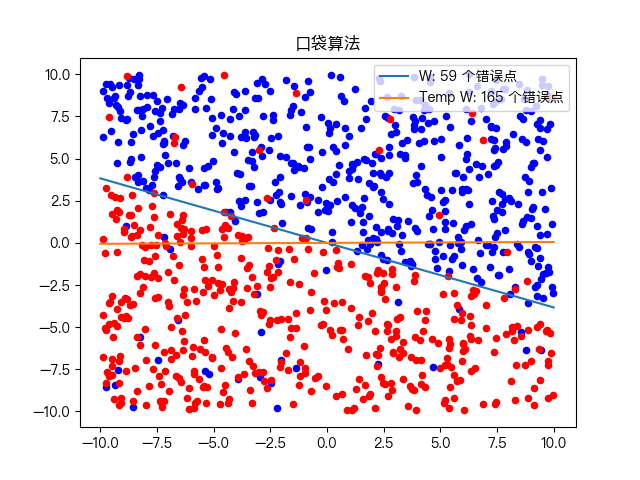
Pocket Algorithm is a binary classification algorithm, which divides a data set into two types through linear combination. As shown in the figure below

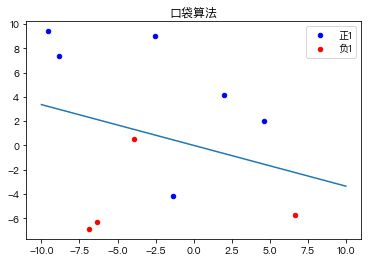
the algorithm is an improvement based on the perceptron learning algorithm. Its core idea is consistent with that of the perceptron learning algorithm and is error driven. If the current result is better than the result in the pocket, replace the result in the pocket with the current result, keep the best result in the pocket, and finally find a relatively good answer, Therefore, it is named pocket algorithm.

3, Algorithm steps

Initialize the vector w, for example, W is initialized to a zero vector

Cycle t = 0, 1, 2

a random error data is found, that is, h(x) does not match the target value y

$$ \operatorname{sign}\left(w_{t}^{T} x_{n(t)}\right) \neq y_{n(t)} $$
try to correct the vector w. if the error point of the updated w is less than that before the update, update w, otherwise enter the next cycle.

$$ w_{t+1} \leftarrow w_{t}+y_{n(t)} x_{n(t)} $$
Exit the cycle until the set maximum number of cycles is reached, and the resulting w is the solution of a set of equations

as can be seen from the above steps, since we don't know when the cycle should stop, we need to manually define a maximum number of cycles as the exit condition, so the running time of pocket algorithm will be slower than perceptron learning algorithm. The error points are randomly selected in the loop, and the final output result is not a stable result in each run.

4, Code implementation

Implement pocket algorithm using Python:

import numpy as np

def errorIndexes(w, X, y):
    """
    Gets the set of subscripts for the error point
    args:
        w - weight coefficient 
        X - Training data set
        y - Target tag value
    return:
        errorIndexes - Subscript set of error points
    """
    errorIndexes = []
    # Traversal training data set
    for index in range(len(X)):
        x = X[index]
        # Determine whether it is inconsistent with the target value
        if x.dot(w) * y[index] <= 0:
            errorIndexes.append(index)
    return errorIndexes

def pocket(X, y, iteration, maxIterNoChange = 10):
    """
    Pocket algorithm implementation
    args:
        X - Training data set
        y - Target tag value
        iteration - Maximum number of iterations
        maxIterNoChange - Number of iterations that did not improve before stopping early
    return:
        w - weight coefficient 
    """
    np.random.seed(42)
    # Initialize weight coefficient
    w = np.zeros(X.shape[1])
    # Gets the set of subscripts for the error point
    errors = errorIndexes(w, X, y)
    iterNoChange = 0
    # loop
    for i in range(iteration):
        iterNoChange = iterNoChange + 1
        # Random acquisition of error point subscript
        errorIndex = np.random.randint(0, len(errors))
        # Calculate temporary weight coefficient
        tmpw = w + y[errors[errorIndex]] * X[errorIndex]
        # Gets the subscript set of error points under the temporary weight coefficient
        tmpErrors = errorIndexes(tmpw, X, y)
        # If the number of error points is less, the weight coefficient is updated
        if len(errors) >= len(tmpErrors):
            iterNoChange = 0
            # Modified weight coefficient
            w = tmpw
            errors = tmpErrors
        # Early stop
        if iterNoChange >= maxIterNoChange:
            break
    return w

5, Animation demonstration

Simple training dataset classification:

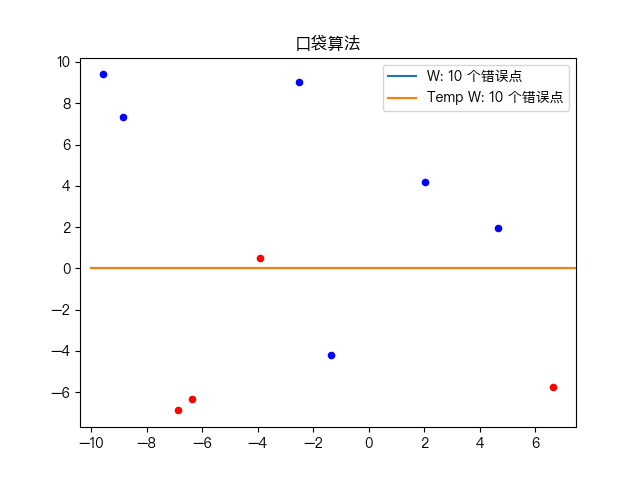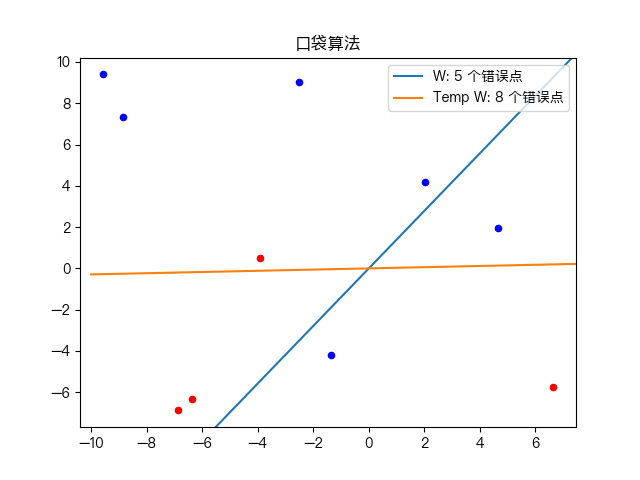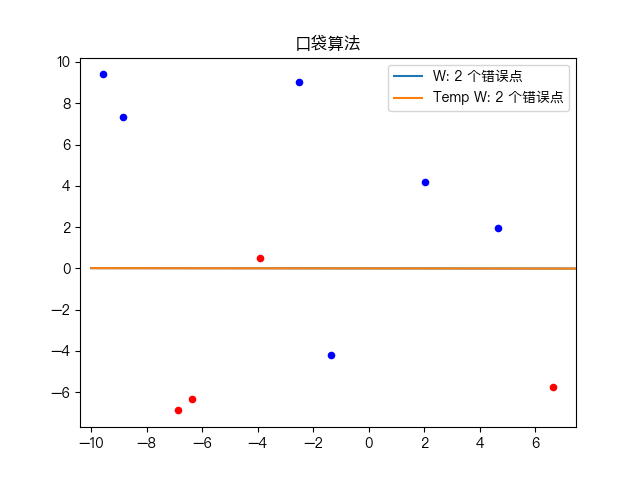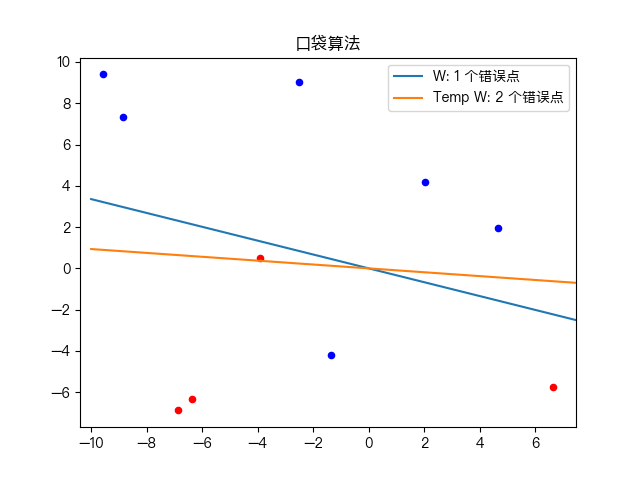
Classification of complex training data sets:

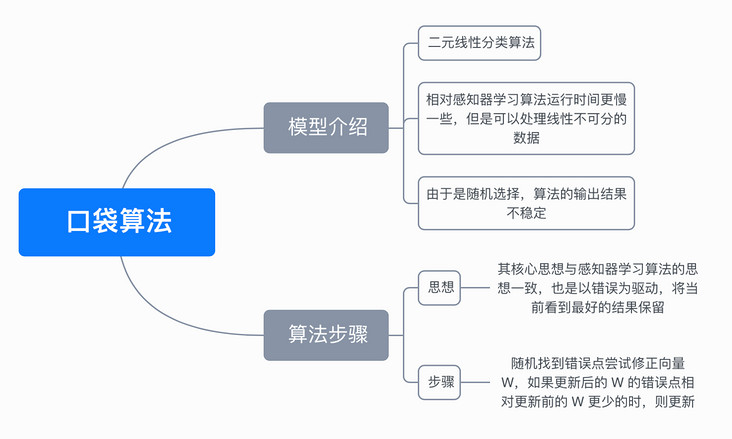
6, Mind map

7, References

For a complete demonstration, please click here

Note: This article strives to be accurate and easy to understand, but as the author is also a beginner, his level is limited. If there are errors or omissions in the article, readers are urged to criticize and correct it by leaving a message

This article was first published in—— AI map , welcome to pay attention

Topics: Algorithm Machine Learning

Programmer Think