1: Introduction

        In the last article, we have a relative understanding of knn algorithm, and roughly understand the working principle and workflow of knn algorithm through a very simple example. This article will continue to analyze the knn Algorithm in depth to help understand the knn algorithm

2: Algorithm analysis

        1. First briefly review the general steps. The knn algorithm can be divided into three steps. The first step is to determine the K value, that is, to find the k data similar to the first k test points. Generally, the value is an integer not greater than 20. The second step is to find the distance between the test point and the sample point. The third part is to determine the type of test points according to the sample rules. The following is a picture found on the Internet.

        2. Value analysis of K

         The following is a picture found on the Internet. When k=3, the determined sample points are within the circle in the figure. At this time, it is natural to judge that the test points are blue triangles according to the statistical rules.

        Similarly, different values of k will also cause errors in the results. The following figure is a representative figure found on the Internet

        

        When k is 3, the test points should be divided into the range of red triangle according to the rules, but when k=5, the test points should be divided into the range of blue square. Therefore, the value of K should be considered. When the number of two or more types of data points within the range is the same, they can be divided according to the distance. The following explains the distance test method.  

         3. Distance test

        For the distance test in knn algorithm, the following test method is generally used, and the test points are represented by (x, y)

        

        This formula is the Euclidean distance formula, which calculates the distance between the test point and the target point. If there are many sample points, add the distance of several points,   The data can be sorted from small to large, and then the main classification of test points can be determined. It is worth mentioning here that for sample points, knn algorithm does not need training, only needs to sum the distance between test points and sample points, so the training process is O (1), and for n groups, m in each group is O (mn)

3. Experimental data analysis

         First, write a function img2vector, convert the image into a vector, create a 1 * 1021 NumPy array, and store the 32 * 32 image character values in the array.

def img2vector(filename):
    returnVect = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect

         Then there is the test code of the identifier

def handwritingClassTest():
    hwLabels = []
    trainingFileList = os.listdir("digits/trainingDigits")
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]
        classNumStr = int(fileStr.split('_')[0])
        hwLabels.append(classNumStr)
        trainingMat[i,:] = img2vector('digits/trainingDigits/%s' %(fileNameStr))
    #Read test data
    testFileList = os.listdir('digits/testDigits')
    errorCount = 0.0
    mTest = len(testFileList)
    errfile = []
    #Loop test each test data file
    for i in range(mTest):
        fileNameStr = testFileList[i]
        fileStr = fileNameStr.split('.')[0]
        classNumStr = int(fileStr.split('_')[0])
        vectorUnderTest = img2vector('digits/testDigits/%s' %(fileNameStr))
        classifierResult = classify0(vectorUnderTest,trainingMat,hwLabels ,3)    
        #Output k-nearest neighbor algorithm classification results and real classification results
        print('the classifier came back with: %d,the real answer is: %d' %(classifierResult,classNumStr))
        #Judge whether the k-nearest neighbor algorithm is accurate
        if(classifierResult != classNumStr):
            errorCount +=1.0
            errfile.append(fileNameStr)
    print('\n the total number of errors is: %d' %(errorCount))         
    print('\n the total error rate is: %f' %(errorCount/float(mTest)))   

Result display

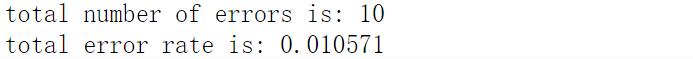
        The output result of the function depends on the machine speed. Loading the data set also requires a lot of data and has a certain error rate. Changing the value of k will also affect the error rate of the algorithm.