what is perceptron

The perceptron receives multiple input signals and outputs one signal.

Perceptron receiving two signals, as shown in the following figure:

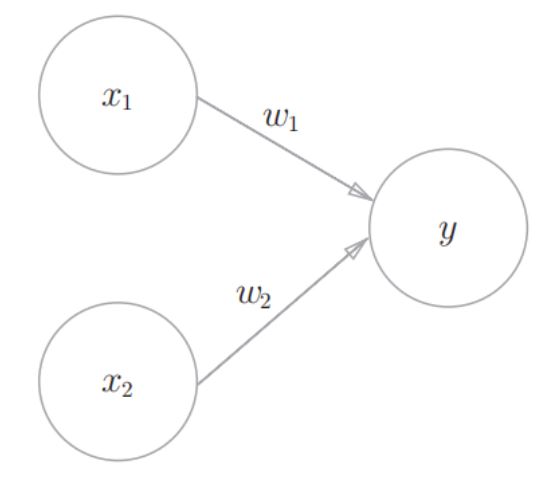
x1 and x2 are input signals; y is the output signal;

w1 and w2 are weights. Circle O represents "neuron" or "node".

**Neurons are activated: * * when x1w1+x2w2 exceeds a certain limit value, y will output 1.

**Threshold value: * * here, the limit value is called the threshold value, which is represented by θ Symbolic representation.

The greater the weight, the higher the importance of the signal corresponding to the weight.

Thus, a mathematical representation of the perceptron can be obtained:

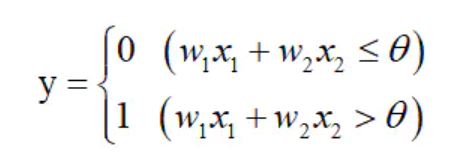
Another mathematical representation of perceptron:

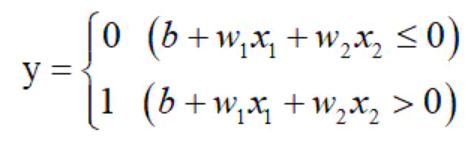
b in the above formula is called offset. The perceptron calculates the product of the input signal and the weight, and then adds the offset. If the value is greater than 0, it outputs 1, otherwise it outputs 0.

Application example of single layer perceptron

Using perceptron, NAND, or NAND gate can be realized.

First, the and gate, both of which are 1, outputs 1:

import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = AND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

Output results:

(0, 0) -> 0
(1, 0) -> 0
(0, 1) -> 0
(1, 1) -> 1

Then there is the OR gate. As long as one of the two inputs is 1, it outputs 1

import numpy as np


def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = OR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

Output results:

(0, 0) -> 0
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 1

Finally, the NAND gate is to reverse the result of and:

import numpy as np

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = NAND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

Output results:

(0, 0) -> 1
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 0

From the above example, we can see that the NAND, or and gate is a perceptron with the same structure, and the only difference is that the values of weight w and bias b are different.

Multilayer perceptron

First, let's look at the truth table of XOR logic:

Enter x1	Enter x2	Output Y
0	0	0
0	1	1
1	0	1
1	1	0

By marking them in the plane coordinate system, it can be found that no straight line can separate the two types of samples.

The mathematical representation of single-layer perceptron is as follows:

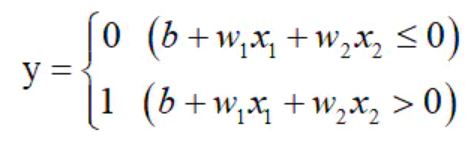
Its geometric meaning: w2x1+w2x2+b=0 is a straight line, which divides two spaces, one space outputs 1 and the other space outputs 0.

In other words, the two types of samples of XOR logic cannot be separated by a single-layer perceptron.

Single layer perceptron can only represent the space divided by a straight line; Nonlinear space: space divided by curves.

And gate, NAND gate, or gate have been realized by single-layer perceptron before. If XOR gate is realized, the front gates can be superimposed.

x1 and x2 represent the input, s1 represents the output of NAND gate, s2 represents the output of or gate, and y represents the output of and gate

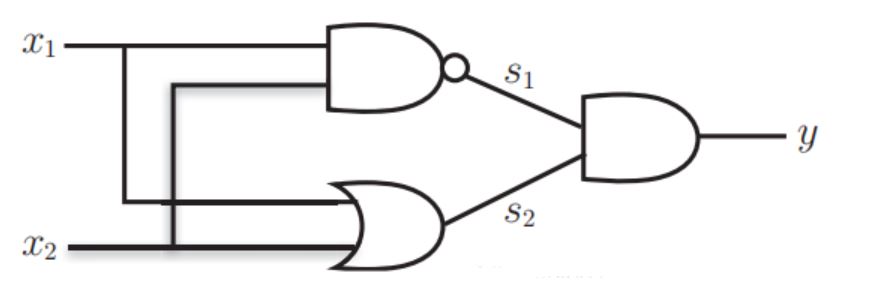
By observing the values of x1, x2 and y, it is found that the output conforms to the XOR gate.

Code to implement XOR gate:

from and_gate import AND
from or_gate import OR
from nand_gate import NAND

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = XOR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

Output results:

(0, 0) -> 0
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 0

It can be seen from the above that the perceptual function can be expressed more flexibly through the superposition layer. If the computer can be realized by combining NAND gates, the computer can also be represented by combining perceptron.

It has been proved that the two-layer perceptron can represent any function, but it is not easy to design the appropriate weight and structure. It is usually constructed by superposition of small modules, such as the above and gate, or gate and NAND gate, and then superimposed to realize XOR gate.