1. Title
Consider the following small games: players use a map, use the initial funds to buy a certain amount of water and food (including food and other daily necessities), start from the starting point and walk in the desert. In case of different weather on the way, you can also supplement funds or resources in mines and villages. The goal is to reach the destination within the specified time and retain as much funds as possible.
The basic rules of the game are as follows:
(1) Take the day as the basic time unit, the start time of the game is day 0, and the player is at the starting point. The player must reach the end point on or before the deadline. After reaching the end point, the player's game ends.
(2) Water and food resources are needed to cross the desert, and their minimum unit of measurement is box. The sum of water and food quality owned by players every day cannot exceed the upper limit of weight bearing. If you don't reach the end point and the water or food is exhausted, the game will be regarded as a failure.
(3) The daily weather is one of the three conditions of "sunny", "high temperature" and "sandstorm", and the weather in all regions of the desert is the same.
(4) Every day, players can go from one area in the map to another area adjacent to it, or stay in place. You must stay where you are on Sandstorm day.
(5) The amount of resources consumed by players staying in place for one day is called the basic consumption, and the amount of resources consumed by walking for one day is times of the basic consumption.
(6) On day 0, players can buy water and food at the base price with initial funds at the starting point. Players can stay at the starting point or return to the starting point, but they cannot buy resources at the starting point multiple times. Players can return the remaining water and food after reaching the destination. The return price of each box is half of the benchmark price.
(7) When players stay in the mine, they can obtain funds through mining. The amount of funds obtained in a day of mining is called basic income. If mining, the amount of resources consumed is times of the basic consumption; If there is no mining, the amount of resources consumed is the basic consumption. No mining is allowed on the day of arrival at the mine. Mining can also be carried out on sandstorm days.
(8) When players pass or stay in the village, they can use the remaining initial funds or the funds obtained from mining to buy water and food at any time. The price of each box is twice the benchmark price.
Please establish a mathematical model according to different settings of the game to solve the following problems.
- Assuming that there is only one player and the weather conditions are known in advance during the whole game period, try to give the player's optimal strategy in general. Solve the "first pass" and "second pass" in the attachment, and fill the corresponding results in the result xlsx.
- Assuming that there is only one player and the player only knows the weather conditions of the day, the player can decide the action plan of the day, try to give the best strategy of the player in general, and discuss the "third level" and "fourth level" in the attachment.
2. Problem solving ideas and the first and second hurdles
There are three main ideas
1. Dynamic planning
2. After simplifying the map, use Dijkstra algorithm to solve it
3. Analyze the problem stem, then establish a model, and use growi and LINGO to solve the optimal solution
2.1 dynamic planning
Let the status dp[k][j][w][f] represent the maximum fund of W box of remaining water and f box of remaining food at point j on day K, then:
ans=MAXw,f,i dp[k][zd][w][f]
2.1.1 initial value setting
Since the starting point can purchase materials at the starting point, there is an initial state
dp[0][qd][w][f]=10000−cost_water∗w−cost_food∗fw∈[0,400]f∈[0,600]
Where cost_water,cost_food is the money consumed to buy water and food.
Assuming that the start is day 0, the weather on the first day affects from day 0 to day 1.
2.1.2 state transition equation
When people are in Village j on day k:
- Day k is sandstorm weather
dp[k+1][j][w+ww-xh_water[tq]][f+ff-xh_food[tq]]}=max(dp[k][j][w][f]-2*ww*cost_water-2*ff*cost_food
- Non sandstorm weather:
dp[k+1][jj][w+ww-xh_water[tq]][f+ff-xh_food[tq]]}=max(dp[k][j][w][f]-2*ww*cost_water-2*ff*cost_food
When people are in the mine j on day k:
mining
dp[k+1][j][w-dig*xh_water[tq]][f-dig*xh_food[tq]]=max(dp[k][j][w][f]+1000)
Day k is sandstorm weather:
dp[k+1][j][w-xh_water[tq]][f-xh_food[tq]]=max(dp[k][j][w][f])
Day k is non sandstorm weather:
dp[k+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]=max(dp[k][jj][w][f])
When people in other areas on day k
Day k is sandstorm weather:
dp[k+1][j][w-xh_water[tq]][f-xh_food[tq]]=max(dp[k][j][w][f])
Day k is non sandstorm weather:
dp[k][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]=max(dp[k][j][w][f])
2.1.3 thinking about implicit constraint model
In addition to returning to the village to replenish supplies, we will not go back.
Except for mining and dust storms, they will not stay in place.
Only the shortest path between keys will be taken
2.1.4 code
First pass
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
// point
const int N=11,M=28,inf=0x3f3f3f,Day=30;
int dp[32][N+1][405][605],zd,qd,FZ;
int cost_water,cost_food,walk,dig,buy;
int xh_water[3]={5,8,10},xh_food[3]={7,6,10};
bool cz[N+1],ks[N+1];
struct node
{
short day; // i
short from; // jj j
int water,food;
int money;
bool operator!=(const node &x){
return x.day!=day || x.from!=from || x.water!=water || x.food!=food ;
};
}path[31][N+1][405][605],lastpath;
vector <int> weather;
vector <int> g[N];
map <int,int> mp;
void push_back(int x,int y)
{
g[x].push_back(y);
g[y].push_back(x);
}
void build_map()
{
push_back(1,2);
push_back(2,3);
push_back(2,5);
push_back(5,6);
push_back(3,4);
push_back(4,7);
push_back(6,7);
push_back(7,8);
push_back(8,9);
push_back(9,10);
push_back(10,11);
mp[1]=1;
mp[2]=25;
mp[3]=26;
mp[4]=27;
mp[5]=24;
mp[6]=23;
mp[7]=21;
mp[8]=9;
mp[9]=15;
mp[10]=14;
mp[11]=12;
for(int i=1;i<=N;i++)
{
cz[i]=0;
ks[i]=0;
}
cz[9]=1;
ks[11]=1;
zd=4;
qd=1;
return ;
}
void init()
{
memset(dp,-inf,sizeof(dp));
FZ=1200;
cost_water=5;
cost_food=10;
walk=2;
buy=2;
dig=3;
for(int k=0;k<=405;k++)
{
for(int l=0;l<=601;l++)
{
if(k*3+l*2<=FZ)
{
dp[0][qd][k][l]=10000-k*cost_water-l*cost_food;
}
}
}
printf("init %d\n",dp[0][1][178][333]);
path[0][1][0][0]={0,0,0,0};
return ;
}
int main()
{
weather={
1,1,0,2,0,1,2,0,1,1,
2,1,0,1,1,1,2,2,1,1,
0,0,1,0,2,1,0,0,1,1,
};
build_map();
init();
for(int i=0;i<Day;i++)
{
printf("The first%d day\n",i);
int tq=weather[i];
for(int j=1;j<=N;j++)
{
if(cz[j])// village
{
for(int w=0;w<=405;w++)
{
for(int f=0;w*3+f*2<=1200;f++)
{
//Purchase or insufficient purchase of materials (ww=0,ff=0 means no purchase)
if(tq==2) //stop
{
int money=dp[i][j][w][f];
for(int ww=0;ww<=money/cost_water;ww++)
{
for(int ff=0;ff<=(FZ-(w+ww)*3)/2-f;ff++)
{
if(w+ww-xh_water[tq]>=0&&f+ff-xh_food[tq]>=0&&dp[i][j][w][f]-2*ww*cost_water-2*ff*cost_food>=0)
{
if(dp[i+1][j][w+ww-xh_water[tq]][f+ff-xh_food[tq]]<dp[i][j][w][f]-2*ww*cost_water-2*ff*cost_food)
{
dp[i+1][j][w+ww-xh_water[tq]][f+ff-xh_food[tq]]=dp[i][j][w][f]-2*ww*cost_water-2*ff*cost_food;
path[i+1][j][w+ww-xh_water[tq]][f+ff-xh_food[tq]]={i,j,w,f,dp[i][j][w][f]-2*ww*cost_water-2*ff*cost_food};
}
}
}
}
}
else //From j to jj
{
for(auto jj:g[j])
{
int money=dp[i][j][w][f];
for(int ww=0;ww<=money/cost_water;ww++)
{
for(int ff=0;ff<=(FZ-(w+ww)*3)/2-f;ff++)
{
if(w+ww-walk*xh_water[tq]>=0&&f+ff-walk*xh_food[tq]>=0&&dp[i][j][w][f]-buy*ww*cost_water-buy*ff*cost_food>=0)
{
if(dp[i+1][jj][w+ww-walk*xh_water[tq]][f+ff-walk*xh_food[tq]]<dp[i][j][w][f]-buy*ww*cost_water-buy*ff*cost_food)
{
dp[i+1][jj][w+ww-walk*xh_water[tq]][f+ff-walk*xh_food[tq]]=dp[i][j][w][f]-buy*ww*cost_water-buy*ff*cost_food;
path[i+1][jj][w+ww-walk*xh_water[tq]][f+ff-walk*xh_food[tq]]={i,j,w,f,dp[i][j][w][f]-buy*ww*cost_water-buy*ff*cost_food};
}
}
}
}
}
}
}
}
}
else if (ks[j])// mine
{
for(int w=0;w<=405;w++)
{
for(int f=0;w*3+f*2<=1200;f++)
{
// I've been here for a day. I can dig
if(w-dig*xh_water[tq]>=0&&f-dig*xh_food[tq]>=0)
{
if(dp[i+1][j][w-dig*xh_water[tq]][f-dig*xh_food[tq]]<dp[i][j][w][f]+1000&&dp[i][j][w][f]>=0)
{
dp[i+1][j][w-dig*xh_water[tq]][f-dig*xh_food[tq]]=dp[i][j][w][f]+1000;
path[i+1][j][w-dig*xh_water[tq]][f-dig*xh_food[tq]]={i,j,w,f,dp[i][j][w][f]+1000};
}
}
// Mining is not allowed or not allowed in the mine
if(tq==2) //Stay without mining
{
if(w-xh_water[tq]>=0&&f-xh_food[tq]>=0)
{
if(dp[i+1][j][w-xh_water[tq]][f-xh_food[tq]]<dp[i][j][w][f]&&dp[i][j][w][f]>=0)
{
dp[i+1][j][w-xh_water[tq]][f-xh_food[tq]]=dp[i][j][w][f];
path[i+1][j][w-xh_water[tq]][f-xh_food[tq]]={i,j,w,f,dp[i][j][w][f]};
}
}
}
else
{
if(w-walk*xh_water[tq]>=0&&f-walk*xh_food[tq]>=0)
{
for(auto jj:g[j])
{
if(dp[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]<dp[i][j][w][f]&&dp[i][j][w][f]>=0)
{
dp[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]=dp[i][j][w][f];
path[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]={i,j,w,f,dp[i][j][w][f]};
}
}
}
}
}
}
}
else //Common area
{
for(int w=0;w<=405;w++)
{
for(int f=0;w*3+f*2<=1200;f++)
{
if(tq==2) //Stop at point j
{
if(w-xh_water[tq]>=0&&f-xh_food[tq]>=0&&dp[i][j][w][f]>=0)
{
if(dp[i+1][j][w-xh_water[tq]][f-xh_food[tq]]<dp[i][j][w][f])
{
dp[i+1][j][w-xh_water[tq]][f-xh_food[tq]]=dp[i][j][w][f];
path[i+1][j][w-xh_water[tq]][f-xh_food[tq]]={i,j,w,f,dp[i][j][w][f]};
}
}
}
else// Go to jj point
{
for(auto jj:g[j])
{
if(w-walk*xh_water[tq]>=0&&f-walk*xh_food[tq]>=0&&dp[i][j][w][f]>=0)
{
if(dp[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]<dp[i][j][w][f])
{
dp[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]=dp[i][j][w][f];
path[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]={i,j,w,f,dp[i][j][w][f]};
}
}
}
}
}
}
}
}
}
int ans=-inf;
node lastpath;
int last_water=0,last_food=0,last_day=Day;
for(int i=0;i<=Day;i++)
{
for(int w=0;w<=405;w++)
for(int f=0;w*3+2*f<=1200;f++)
{
if(dp[i][zd][w][f]>ans)
{
ans=dp[i][zd][w][f];
lastpath=path[i][zd][w][f];
last_water=w;
last_food=f;
last_day=i;
}
}
}
stack<node> s;
stack<int> my;
printf("??day:%d weather:%d %d water:%d food:%d money:%d\n",last_day,weather[Day],zd,last_water,last_food,ans);
s.push((node){last_day,zd,last_water,last_food,ans});
while(lastpath!=path[0][1][0][0])
{
s.push(lastpath);
printf("??day:%d weather:%d %d water:%d food:%d money:%d\n",lastpath.day,weather[lastpath.day],mp[lastpath.from],lastpath.water,lastpath.food,lastpath.money);
my.push(lastpath.money);
lastpath=path[lastpath.day][lastpath.from][lastpath.water][lastpath.food];
}
freopen("output.txt","w",stdout);
my.push(my.top());
while (!s.empty())
{
node t=s.top();
int money=my.top();
printf("Day:%d weather:%d point:%d water:%d food:%d money:%d\n",t.day,weather[t.day],mp[t.from],t.water,t.food,money);
s.pop();
my.pop();
}
printf("%d\n",ans);
return 0;
}
Second pass
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const short N=27,inf=20000,Day=30;
short dp[31][N+1][401][601],zd,qd,FZ;
short cost_water,cost_food,walk,dig,buy;
short xh_water[3]={5,8,10},xh_food[3]={7,6,10};
bool cz[N+1],ks[N+1];
struct node
{
char day; // i
char from; // jj j
short water,food;
bool operator!=(const node &x){
return (x.day-'0')!=(day-'0') || (x.from-'0'!=from-'0') || (x.water-'0')!=(water-'0') || (x.food-'0'!=food-'0') ;
};
}path[31][N+1][401][601],lastpath;
vector <short> weather;
vector <short> g[N+1];
map <short,short> mp;
void push_back(short x,short y)
{
g[x].push_back(y);
g[y].push_back(x);
}
void build_map(short flag)
{
if(flag==2)
{
push_back(1,2);
push_back(2,3);
push_back(3,4);
push_back(4,5);
push_back(5,6);
push_back(6,7);
push_back(7,8);
push_back(8,9);
push_back(9,10);
push_back(10,11);
push_back(11,12);
push_back(7,13);
push_back(13,14);
push_back(14,15);
push_back(15,16);
push_back(15,10);
push_back(15,11);
push_back(16,12);
push_back(3,17);
push_back(17,18);
push_back(18,19);
push_back(19,20);
push_back(20,21);
push_back(21,22);
push_back(22,23);
push_back(15,23);
push_back(23,16);
mp[1]=1;
mp[2]=2;
mp[3]=3;
mp[4]=4;
mp[5]=12;
mp[6]=21;
mp[7]=29;
mp[8]=30;
mp[9]=39;
mp[10]=47;
mp[11]=56;
mp[12]=64;
mp[13]=38;
mp[14]=46;
mp[15]=55;
mp[16]=63;
mp[17]=11;
mp[18]=20;
mp[19]=28;
mp[20]=37;
mp[21]=45;
mp[22]=54;
mp[23]=62;
for(short i=1;i<=N;i++)
{
cz[i]=0;
ks[i]=0;
}
cz[9]=cz[23]=1;
ks[8]=ks[15]=1;
qd=1;
zd=12;
}
return ;
}
void init()
{
FZ=1200;
cost_water=5;
cost_food=10;
walk=2;
buy=2;
dig=3;
for(short i=0;i<=Day;i++)
{
for(short j=1;j<=N;j++)
{
for(short w=0;w<=400;w++)
{
for(short f=0;f<=600;f++)
{
if(w*3+f*2<=FZ)
{
dp[i][j][w][f]=-inf;
}
}
}
}
}
for(short k=10;k<=405;k++)
{
for(short l=0;k*3+l*2<=FZ;l++)
{
dp[0][qd][k][l]=10000-k*cost_water-l*cost_food;
}
}
path[0][1][0][0]={0,0,0,0};
return ;
}
int main()
{
weather={
1,1,0,2,0,1,2,0,1,1,
2,1,0,1,1,1,2,2,1,1,
0,0,1,0,2,1,0,0,1,1,
};
build_map(2);
init();
// dp [i][j][w][f]
// On the i day, the maximum profit was obtained when j points were w tanks of water and f tanks of food,
// max_k_l (dp[30][27][k][l])
// The weather on day i determines whether day i+1 can move
// For example, the weather on day 0 determines whether it can move on day 1
// The situation of non voluntary stay in the mine will not be considered first
// for(short i=1;i<N;i++)
// {
// printf("point% d", i);
// for(auto j:mp[i])
// {
// printf("%d ",j);
// }
// printf("\n");
// }
// printf("???%d %d %d %d\n",xh_food[0],xh_food[2],xh_water[0],xh_water[1]);
for(short i=0;i<Day;i++)
{
printf("The first%d day\n",i);
short tq=weather[i];
for(short j=1;j<=N;j++)
{
if(cz[j])// village
{
for(short w=0;w<=405;w++)
{
for(short f=0;w*3+f*2<=1200;f++)
{
//Purchase or insufficient purchase of materials (ww=0,ff=0 means no purchase)
if(tq==2) //stop
{
short money=dp[i][j][w][f];
for(short ww=0;ww<=money/cost_water;ww++)
{
for(short ff=0;ff<=(FZ-(w+ww)*3)/2-f;ff++)
{
if(w+ww-xh_water[tq]>=0&&f+ff-xh_food[tq]>=0&&dp[i][j][w][f]-2*ww*cost_water-2*ff*cost_food>=0)
{
if(dp[i+1][j][w+ww-xh_water[tq]][f+ff-xh_food[tq]]<dp[i][j][w][f]-2*ww*cost_water-2*ff*cost_food)
{
dp[i+1][j][w+ww-xh_water[tq]][f+ff-xh_food[tq]]=dp[i][j][w][f]-2*ww*cost_water-2*ff*cost_food;
// path[i+1][j][w+ww-xh_water[tq]][f+ff-xh_food[tq]]={i,j,w,f,dp[i][j][w][f]-2*ww*cost_water-2*ff*cost_food};
path[i+1][j][w+ww-xh_water[tq]][f+ff-xh_food[tq]]={i,j,w,f};
}
}
}
}
}
else //From j to jj
{
for(auto jj:g[j])
{
short money=dp[i][j][w][f];
for(short ww=0;ww<=money/cost_water;ww++)
{
for(short ff=0;ff<=(FZ-(w+ww)*3)/2-f;ff++)
{
if(w+ww-walk*xh_water[tq]>=0&&f+ff-walk*xh_food[tq]>=0&&dp[i][j][w][f]-buy*ww*cost_water-buy*ff*cost_food>=0)
{
if(dp[i+1][jj][w+ww-walk*xh_water[tq]][f+ff-walk*xh_food[tq]]<dp[i][j][w][f]-buy*ww*cost_water-buy*ff*cost_food)
{
dp[i+1][jj][w+ww-walk*xh_water[tq]][f+ff-walk*xh_food[tq]]=dp[i][j][w][f]-buy*ww*cost_water-buy*ff*cost_food;
// path[i+1][jj][w+ww-walk*xh_water[tq]][f+ff-walk*xh_food[tq]]={i,j,w,f,(short)dp[i][j][w][f]-buy*ww*cost_water-buy*ff*cost_food};
path[i+1][jj][w+ww-walk*xh_water[tq]][f+ff-walk*xh_food[tq]]={i,j,w,f};
}
}
}
}
}
}
}
}
}
else if (ks[j])// mine
{
for(short w=0;w<=405;w++)
{
for(short f=0;w*3+f*2<=1200;f++)
{
// I've been here for a day. I can dig
if(w-dig*xh_water[tq]>=0&&f-dig*xh_food[tq]>=0)
{
if(dp[i+1][j][w-dig*xh_water[tq]][f-dig*xh_food[tq]]<dp[i][j][w][f]+1000&&dp[i][j][w][f]>=0)
{
dp[i+1][j][w-dig*xh_water[tq]][f-dig*xh_food[tq]]=dp[i][j][w][f]+1000;
// path[i+1][j][w-dig*xh_water[tq]][f-dig*xh_food[tq]]={i,j,w,f,(short)dp[i][j][w][f]+1000};
path[i+1][j][w-dig*xh_water[tq]][f-dig*xh_food[tq]]={i,j,w,f};
}
}
// Mining is not allowed or not allowed in the mine
if(tq==2) //Stay without mining
{
if(w-xh_water[tq]>=0&&f-xh_food[tq]>=0)
{
if(dp[i+1][j][w-xh_water[tq]][f-xh_food[tq]]<dp[i][j][w][f]&&dp[i][j][w][f]>=0)
{
dp[i+1][j][w-xh_water[tq]][f-xh_food[tq]]=dp[i][j][w][f];
// path[i+1][j][w-xh_water[tq]][f-xh_food[tq]]={i,j,w,f,dp[i][j][w][f]};
path[i+1][j][w-xh_water[tq]][f-xh_food[tq]]={i,j,w,f};
}
}
}
else
{
if(w-walk*xh_water[tq]>=0&&f-walk*xh_food[tq]>=0)
{
for(auto jj:g[j])
{
if(dp[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]<dp[i][j][w][f]&&dp[i][j][w][f]>=0)
{
dp[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]=dp[i][j][w][f];
// path[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]={i,j,w,f,dp[i][j][w][f]};
path[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]={i,j,w,f};
}
}
}
}
}
}
}
else //Common area
{
for(short w=0;w<=405;w++)
{
for(short f=0;w*3+f*2<=1200;f++)
{
if(tq==2) //Stop at point j
{
if(w-xh_water[tq]>=0&&f-xh_food[tq]>=0&&dp[i][j][w][f]>=0)
{
if(dp[i+1][j][w-xh_water[tq]][f-xh_food[tq]]<dp[i][j][w][f])
{
dp[i+1][j][w-xh_water[tq]][f-xh_food[tq]]=dp[i][j][w][f];
// path[i+1][j][w-xh_water[tq]][f-xh_food[tq]]={i,j,w,f,dp[i][j][w][f]};
path[i+1][j][w-xh_water[tq]][f-xh_food[tq]]={i,j,w,f};
}
}
}
else// Go to jj point
{
for(auto jj:g[j])
{
if(w-walk*xh_water[tq]>=0&&f-walk*xh_food[tq]>=0&&dp[i][j][w][f]>=0)
{
if(dp[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]<dp[i][j][w][f])
{
dp[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]=dp[i][j][w][f];
// path[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]={i,j,w,f,dp[i][j][w][f]};
path[i+1][jj][w-walk*xh_water[tq]][f-walk*xh_food[tq]]={i,j,w,f};
}
}
}
}
}
}
}
}
}
short ans=-inf;
node lastpath;
short last_water=0,last_food=0,last_day=Day;
for(short i=0;i<=Day;i++)
{
for(short w=0;w<=405;w++)
for(short f=0;w*3+2*f<=1200;f++)
{
if(dp[i][zd][w][f]>ans)
{
ans=dp[i][zd][w][f];
lastpath=path[i][zd][w][f];
last_water=w;
last_food=f;
last_day=char(i);
}
}
}
stack<node> s;
// freopen("outputQ2.txt","w",stdout);
printf("ans:%d\n",ans);
printf("day:%d weather:%d point:%d water:%d food:%d\n",last_day,weather[Day],zd,last_water,last_food);
node temppath=(node){last_day,zd,last_water,last_food};
s.push(temppath);
while(lastpath!=path[0][1][0][0])
{
s.push(lastpath);
printf("day:%d weather:%d point %d water:%d food:%d\n",lastpath.day,(int)weather[lastpath.day],(int)mp[lastpath.from],lastpath.water,lastpath.food);
temppath=lastpath;
lastpath=path[lastpath.day][lastpath.from][lastpath.water][lastpath.food];
}
}
2.2 simplified map + Dijkstra
2.2.1 model simplification and analysis
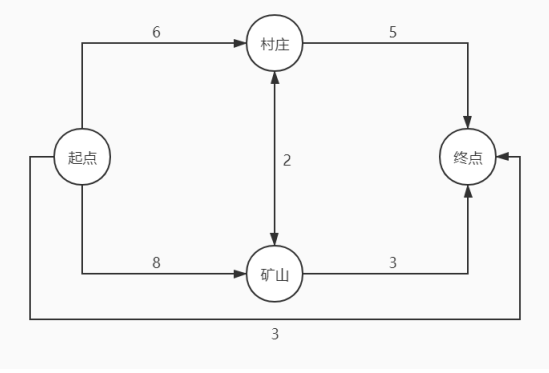
The original map of the game is more complex, but in fact, the meaningful nodes are only the starting point, the ending point, the village and the mine. Therefore, Dijkstra is considered to be used to calculate the shortest path of these four types of nodes, and the original map is compressed to contain only four types of nodes.
The following is a discussion and analysis of various issues
For the situation where there is only one player and the weather is known every day: the first level and the second level must have a definite optimal solution, and the map structure is not complex, so it can be solved directly by exhaustive search strategy, Monte Carlo search strategy and so on.
2.2.2 model assumptions
1. Daily weather conditions are independent of each other.
2. Players determine strategies every morning and complete state transfer and resource and capital settlement at night.
3. In multiplayer games, each player is absolutely selfish and completely rational.
2.2.3 symbol description

2.2.4 model establishment and solution
maxQ30+12pwW30+12pfF30
QT, WT and FT respectively represent the amount of money, water and food left by the player on day t. If the player reaches the end point before the 30th day, its attributes will be regarded as unchanged in the next few days, so we take the 30th day as the unified end time. The objective function has the following constraints: Qt=Qt − 1+QMineMinet − Shopt[2pfShopFt+2pwShopWt]
Food
The fund at the end of each day is equal to the fund of the previous day plus 1000 yuan obtained from mining on the same day (if mining), and then minus the money for buying food and water in the village (if buying). ShopFt and ShopWt respectively represent the amount of food and water purchased by the player on day t (if purchased).
Ft=F(t−1)−2Movet △Ft− 3Mine tMovet △Ft−(1−Movet−Minet)△Ft+Shopt ShopFt
Water aspect
Wt=Wt−1−2Movet△Wt−3Minet△Wt−(1−Movet−Minet)△Wt+ShoptShopWt
2.2.5 map simplification
We first introduce Dijkstra algorithm, which is an efficient algorithm for finding the shortest path between two points in a directed weighted graph. Select the starting point, ending point, village and mine in the figure as special points, and use Dijkstra algorithm to calculate the shortest path between each two special points (i.e. the minimum number of days required without considering the influence of sandstorm weather). Simplify a new map according to the situation.
# encoding: utf-8
# init_water=180
# init_food=330
init_water=184
init_food=324
money=10000-init_food*10-init_water*5
weather=["high temperature","high temperature","sunny","Sandstorm","sunny",
"high temperature","Sandstorm","sunny","high temperature","high temperature",
"Sandstorm","high temperature","sunny","high temperature","high temperature",
"high temperature","Sandstorm","Sandstorm","high temperature","high temperature",
"sunny","sunny","high temperature","sunny","Sandstorm",
"high temperature","sunny","sunny","high temperature","high temperature"
]
base_consume_water=[5,8,10]
base_consume_food=[7,6,10]
def get_weather(i):
if i=="high temperature":
return 1
if i=="sunny":
return 0
else:
return 2
def go(hhday,road):
already_go=0
consume_water=0
consume_food=0
while already_go<road:
if hhday>30:
return -1,-1,-1
if get_weather(weather[hhday-1])!=2:
#print(hhday,"Day go",weather[hhday])
consume_food+=base_consume_food[get_weather(weather[hhday-1])]*2
consume_water+=base_consume_water[get_weather(weather[hhday-1])]*2
hhday+=1
already_go+=1
else:
#print(hhday, "Day dont go")
consume_food += base_consume_food[get_weather(weather[hhday-1])]
consume_water += base_consume_water[get_weather(weather[hhday-1])]
hhday += 1
return consume_water,consume_food,hhday
base_water_price=5
base_water_weight=3
base_food_price=10
base_food_weight=2
def possess_c(cur_water,cur_food,cur_money,cur_day,log):
can_take=1200-cur_water*3-cur_food*2
#print(can_take)
#print(cur_money)
log=log+"At Day "+str(cur_day)+": "+"Reach c water and food "+str(cur_water)+" "+str(cur_food)+"\n"
i=0
if cur_day>18:
# Prepare for the return trip and carry only enough materials to reach the destination as far as possible
temp_water=max(36,cur_water)
temp_food=max(40,cur_food)
i=temp_water-cur_water
j=temp_food-cur_food
temp_money = cur_money - i* base_water_price * 2-j*base_food_price*2
else:
# Since the starting point tends to buy food with better cost performance, it tends to buy backpacks filled with water
i=int(can_take/base_water_weight)
j=0
temp_water=cur_water+i
temp_food=cur_food
temp_money=cur_money-i*base_water_price*2
newlog=log+"At Day "+str(cur_day)+": "+"Buy water and food "+str(i)+" "+"\n"
q,w,e=go(cur_day,3)
temp_water1=temp_water-q
temp_food1=temp_food-w
newlog+="At Day "+str(e)+": "+"Move End water and food "+str(temp_water1)+" "+str(temp_food1)+"\n"
possess_z(temp_water1,temp_food1,temp_money,e,newlog)
newlog = log+"At Day "+str(cur_day)+": "+"Buy water and food "+str(i)+ "\n"
q, w, e = go(cur_day, 2)
temp_water2 = temp_water - q
temp_food2 = temp_food - w
newlog += "At Day " + str(e) + ": " + "Move Mine water and food " + str(temp_water2) + " " + str(
temp_food2) + "\n"
posseess_k(temp_water2, temp_food2, temp_money, e,newlog)
log_list={}
def possess_z(cur_water,cur_food,cur_money,cur_day,log):
#print("END ",cur_water*5/2+cur_food*10/2+cur_money,cur_day)
log+="End "+str(cur_day)+" "+str(cur_water*5/2+cur_food*10/2+cur_money)
if cur_water<0 or cur_food<0:
return -1
log_list[log]=cur_water*5/2+cur_food*10/2+cur_money
return cur_water*5/2+cur_food*10/2+cur_money
def posseess_k(cur_water,cur_food,cur_money,cur_day,log):
log = log + "At Day " + str(cur_day) + ": " + "Reach M water and food " + str(cur_water) + " " + str(
cur_food) + "\n"
water_limit=cur_water/(base_consume_water[get_weather("sunny")]*3)
food_limit=cur_food/(base_consume_food[get_weather("sunny")]*3)
total_limit=int(min(water_limit,food_limit))
total_limit=min(total_limit,30-cur_day)
for i in range(1,total_limit+1):
temp_food=cur_food
temp_water=cur_water
temp_day=cur_day
newlog=log
temp_money=cur_money
for j in range(1,i+1):
temp_water=temp_water-base_consume_water[get_weather(weather[cur_day+j-2])]*3
temp_food=temp_food-base_consume_food[get_weather(weather[cur_day+j-2])]*3
temp_day+=1
temp_money+=1000
newlog+="At Day " + str(temp_day) + ": " + "Dig " + str(j)+" Days "+str(temp_water) + " " + str(
temp_food) +" " + str(temp_money)+ "\n"
q, w, e = go(temp_day, 2)
if q < 0:
continue
temp_water2 = temp_water - q
temp_food2 = temp_food - w
if temp_food2 < 0 or temp_water2 < 0:
continue
newlog += "At Day " + str(e) + ": " + "Go Village water and food " + str(temp_water2) + " " + str(
temp_food2) + "\n"
possess_c(temp_water2, temp_food2, temp_money, e, newlog)
q,w,e=go(temp_day,5)
if q<0:
continue
temp_water1=temp_water-q
temp_food1=temp_food-w
if temp_food1<0 or temp_water1<0:
continue
newlog += "At Day " + str(e) + ": " + "Go end water and food " + str(temp_water1) + " " + str(
temp_food1) + "\n"
possess_z(temp_water1,temp_food1,temp_money,e,newlog)
def check(i,j):
if 3*i+2*j>1200 or 5*i+10*j>10000:
return False
else:
return True
def train():
i=0
for init_water in range(150,200):
for init_food in range(300,360):
i+=1
if check(init_water, init_food):
q,w,e=go(1,6)
log=""
possess_c(init_water-q,init_food-w,money,e,log)
print(i)
train()
max=-1
max_index=0
for i in log_list:
if log_list[i]>max:
max=log_list[i]
max_index=i
print(max_index)
3. The third and fourth levels
Compared with the first two levels, the third level only knows the weather of the day, determines the action plan of the day and gives the best strategy.
3.1 summary of the first two levels
Analyze the first pass and the second pass: the following basic strategy design principles can be obtained
(1) The resources at the destination are just exhausted. In order to have as much money as possible when reaching the destination, there is no reason for the universal joint to buy excess water and food for survival. The price of resources purchased by the player at seven o'clock and in the village is higher than the money returned at the destination. Therefore, when the weather conditions are known, the player knows the minimum resources needed to maintain his survival, Therefore, it has the ability to control that the resources are just exhausted when it reaches the end point. This strategy is only applicable when the global weather is known. The third and fourth levels are not allowed.
(2) Buy more food at the starting point to ensure survival
Because the resources in the village are expensive, they should buy food from the starting point as much as possible, and because there is an upper limit on backpacks, players tend to buy resources with higher price and lower quality from the starting point. Will buy as much food as possible.
3.2 three levels
Due to the randomness of the third and fourth levels, it is not possible to give a deterministic optimal strategy, so it is necessary to evaluate the results of the scheme after designing the scheme
Follow the idea of dynamic programming to deal with the third pass
The weather of the third level is random. However, the map is relatively small and has only 10 days. In all weather conditions, the optimal solution of each situation can be given by dynamic programming, and the law can be observed by statistical method.
By observing the optimal solution strategy, it is found that even in all sunny days, there is not all mining. It can be guessed that mining cannot be carried out at this level.
In fact, because there are no villages in the third pass, and because the high temperature weather consumes more and the mining income is smaller, even if mining in sunny weather, the income is only 200-165 = 35, and the income 175 in five days of mining can not make up for the resource loss caused by detour. Therefore, it is a more correct choice to go directly to the destination.
3.3 four closures
The fourth level is compared with the previous level, and a new concept decision point is introduced. This decision point 13 is only 4 days away from the starting point, and it is a necessary point for players in the desert, which is very similar to the situation of the third level. At the same time, the decision-making point is only one day away from the village and mine. The installation point at the decision-making point directly affects the player's decision-making, so it is the key point for the player to make decision-making.
Analyze the most effective strategy in general
There are no mines and villages in the map
When the player is close to the next destination, the player should not wait, but reach the destination as much as possible, because a longer stay will greatly increase the consumption of resources and even the risk of failure. Even if the final destination can be reached, the final capital is almost the same as the quick pass scheme, Not much money is saved by walking away from the heat.
There are villages and mines on the map
The starting point strategy is to carry efficient resources and supplement a large number of inefficient resources in villages
The action strategy is to make a decision at the point close to the village and mine. If there are few resources, supplement the resources first. If there are many resources, dig the mine. When the remaining resources are excavated, it is only enough to go to the next function point according to the worst plan.
3.4 how to deal with the weather
One way to deal with the weather is to generate it randomly according to a certain distribution, and then count each situation and analyze the most effective strategy.
Another is to use Markov chain to establish a weather prediction model. Predict the weather conditions of other levels according to the weather conversion conditions of the first level, and obtain the best strategy of players under different weather conditions according to the model of problem 1. Using the corresponding weather probability and the maximum capital under the best strategy, we can obtain the mathematical expectation of final income and choose the strategy with the greatest mathematical expectation
4. Use software and programming language
Use different tools according to different ideas of solving problems;
If dynamic programming is used as the main solution method, C + + and Matlab can be used as the solution method.
If we focus on Simulation and simulation, we can solve it by Monte Carlo method. This can be done using Python.
If the solver such as groupI is used, it can be used together with MATLAB and programming language.
In the second part of this paper, the code of dynamic programming to solve the first and second hurdles comes from
https://www.cnblogs.com/cherrypill/p/15158527.html