subject

40 students need to be assigned to 10 dormitories. We got these 40 students through the questionnaire
As shown in the figure below, the complete data is in excel:

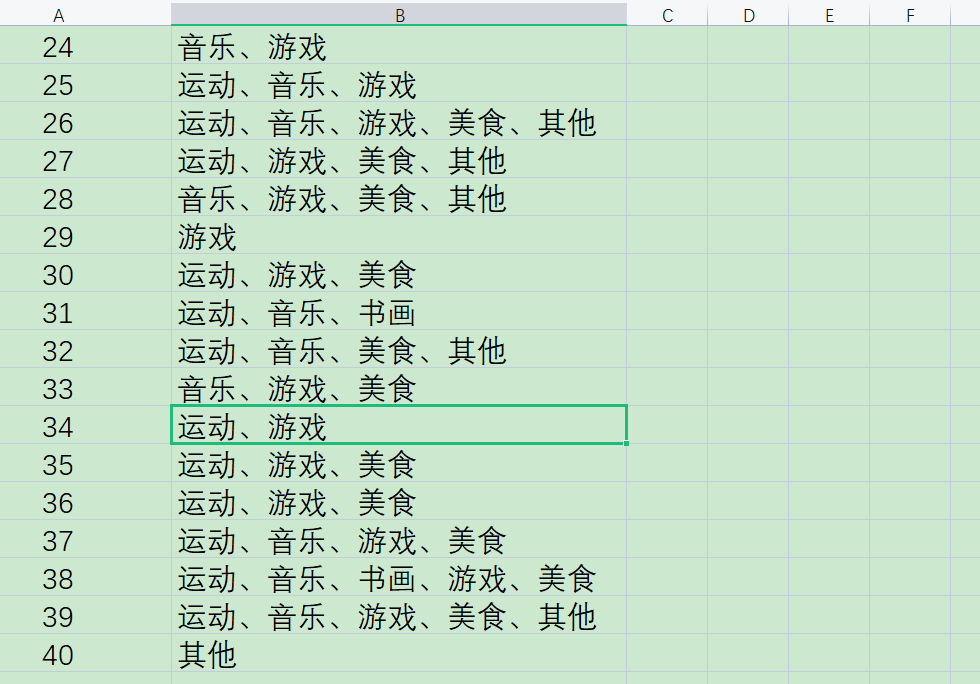
How to divide dormitories can ensure that the number of common hobbies of students in different dormitories and the same dormitories are distributed as evenly as possible.

thinking

(1) How to understand the distribution of the number of common hobbies of students in the same dormitory between different dormitories? The distribution is as uniform as possible: the variance (standard deviation) is as small as possible!
Take each dormitory as a whole, and first calculate the number of common hobbies of the four students in the dormitory.
For example, the notation (x,y) indicates the number of common hobbies of X and y students. If there are four ABCD students in a dormitory, the number of common hobbies in this dormitory should be equal to: (A,B)+(A,C)+(A,D)+(B,C)+(B,D)+(C,D). Then, we calculate the number of common hobbies of four students in each dormitory in 10 bedrooms, record it in the tmp vector, and then calculate the variance or standard deviation of this vector, Our objective function is to make the variance or standard deviation of tmp as small as possible.
(2) How to preprocess data?
Step 1: delete the other item in the interest because it is too broad.
Step 2: regard each student's interest as a set (the elements in the set are mutually exclusive),
The common interests of any two students can be calculated by using the "intersection ∩" operation between sets
Calculate the number of elements in this set to get the common interests and love of any two students
Good count.
(3) What method is used to find the optimal partition scheme?
We can consider using simulated annealing algorithm here. 40 students were replaced by 1-40.
Define the initial solution: a random arrangement of 1-40
For example: 39, 5, 7, 16, 21, 3, 31, 17,..., 9, 21, 19, 2. Every four locations are divided into a dormitory.
Objective function: the standard deviation of the number of common hobbies in 10 bedrooms should be as small as possible
The way to generate new solutions: similar to the traveling salesman problem (TSP)

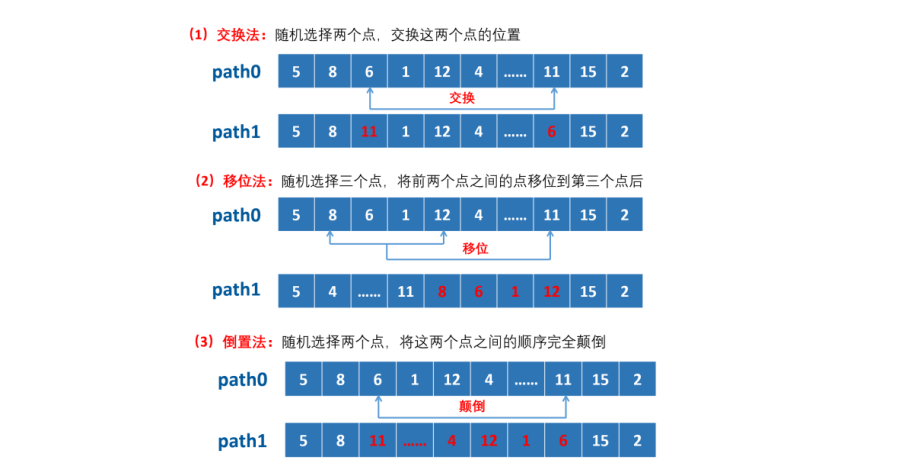
(4) Is there anything else that can be improved?
Suppose that in scheme 1, the number of common hobbies in each bedroom is equal to 10; In scheme 2, the number of common hobbies in each bedroom is equal to 12, Then, the objective functions calculated by scheme 1 and scheme 2 are equal to 0 (the same elements in a group mean no fluctuation, and the standard deviation is 0), but it is obvious that we prefer scheme 2. Therefore, while ensuring that the distribution of the number of common hobbies of students in each dormitory is as uniform as possible, the more the number of common hobbies in the dormitory, the better. (multi-objective problem).
Define a new objective function: (std(tmp) + 1) /max(tmp). The smaller the objective function, the better

code

python version:

import numpy as np
import pandas as pd
df = pd.read_csv(r'C:\Users\sxjmqf\Desktop\data.csv')
data = df.iloc[:,1].tolist()
data = [set(i.replace('other','').strip(',').split(',')) for i in data]
result = [len(i & j) for i in data for j in data]
result = np.array(result).reshape(len(data),-1)
np.savetxt(r'C:\Users\sxjmqf\Desktop\mydata.csv', result, delimiter=',')

matlab code is too troublesome. It is not recommended, but let's show it:
calculate_ans.m

function [ans,tmp] = calculate_ans(path,mydata)
    n = length(path);  % Number of students
    nums = n  / 4;   % Number of dormitories
    path = reshape(path,4,nums);  % Every four people are assigned to a bedroom
    tmp = zeros(1,nums);  % tmp Used to keep the number of common hobbies in each bedroom
    for i = 1 : nums
        tmp(i) = get_total_hobby(path(:,i),mydata);  % Call the sub function to calculate the number of common hobbies of four students in each dormitory separately
    end
%     ans = std(tmp);   % Calculate standard deviation
    ans = (std(tmp) + 1)  / max(tmp);
%     ans = (std(tmp) + 1)  / mean(tmp);
end

gen_new_path.m (it can be imagined that matlab processing files is really a little old)

function path1 = gen_new_path(path0)
    % path0: Original path
    n = length(path0);
    % Two methods of generating new paths are randomly selected
    p1 = 0.33;  % The probability of generating a new path using the exchange method
    p2 = 0.33;  % The probability of generating a new path using the shift method
    r = rand(1); % Randomly generate a[0 1]Uniformly distributed random numbers between
    if  r< p1    % Generate new path using exchange method 
        c1 = randi(n);   % Generate 1-n A random integer in
        c2 = randi(n);   % Generate 1-n A random integer in
        path1 = path0;  % take path0 Value assigned to path1
        path1(c1) = path0(c2);  %change path1 The first c1 The element at position is path0 The first c2 Elements in multiple locations
        path1(c2) = path0(c1);  %change path1 The first c2 The element at position is path0 The first c1 Elements in multiple locations
    elseif r < p1+p2 % Generate new path using shift method
        c1 = randi(n);   % Generate 1-n A random integer in
        c2 = randi(n);   % Generate 1-n A random integer in
        c3 = randi(n);   % Generate 1-n A random integer in
        sort_c = sort([c1 c2 c3]);  % yes c1 c2 c3 Sort from small to large
        c1 = sort_c(1);  c2 = sort_c(2);  c3 = sort_c(3);  % c1 < = c2 <=  c3
        tem1 = path0(1:c1-1);
        tem2 = path0(c1:c2);
        tem3 = path0(c2+1:c3);
        tem4 = path0(c3+1:end);
        path1 = [tem1 tem3 tem2 tem4];
    else  % Generate new path using inversion method
        c1 = randi(n);   % Generate 1-n A random integer in
        c2 = randi(n);   % Generate 1-n A random integer in
        if c1>c2  % If c1 than c2 Big, exchange c1 and c2 Value of
            tem = c2;
            c2 = c1;
            c1 = tem;
        end
        tem1 = path0(1:c1-1);
        tem2 = path0(c1:c2);
        tem3 = path0(c2+1:end);
        path1 = [tem1 fliplr(tem2) tem3];   %Left and right symmetric flip of matrix fliplr，Flip up and down symmetrically flipud
    end
end

get_total_hobby.m

function hobby = get_total_hobby(path,mydata)
% path: Number of four students in the same dormitory
% mydata: Number of common hobbies between each two students
    hobby = 0;
    for i = 1 : 4
        for j = 1:i
            if i ~= j
                hobby = hobby+mydata(path(i), path(j));
            end
        end
    end
end

Main function: main m

clear;clc
tic
rng('shuffle')  % Controls the generation of random numbers, otherwise it is opened every time matlab The results are the same
% https://ww2.mathworks.cn/help/matlab/math/why-do-random-numbers-repeat-after-startup.html
% https://ww2.mathworks.cn/help/matlab/ref/rng.html
n = 40;  % How many students are there
mydata = csvread('C:\Users\sxjmqf\Desktop\mydata.csv');

%% Parameter initialization
T0 = 1000;   % initial temperature 
T = T0; % The temperature will change during the iteration. The temperature is zero at the first iteration T0
maxgen = 500;  % Maximum number of iterations
Lk = 500;  % Number of iterations per temperature
alpfa = 0.95;  % Temperature attenuation coefficient

%%  Randomly generate an initial solution
path0 = randperm(n);
result0 = calculate_ans(path0,mydata);  % Calculate the standard deviation corresponding to this set of solutions

%% Define some quantities for saving intermediate processes to facilitate output results and drawing
min_result = result0;    
RESULT = zeros(maxgen,1); % Record the results found at the end of each outer cycle min_result ((convenient for drawing)

%% Simulated annealing process
for iter = 1 : maxgen  % External circulation, What I use here is to specify the maximum number of iterations
    for i = 1 : Lk  %  Internal circulation, starting iteration at each temperature
        path1 = gen_new_path(path0);  
        result1 = calculate_ans(path1,mydata); 
        if result1 < result0    
            path0 = path1; 
            result0 = result1; 
        else
            p = exp(-(result1 - result0)/T); % according to Metropolis The criterion calculates a probability
            if rand(1) < p   % Generate a random number and compare it with this probability. If the random number is less than this probability
                path0 = path1;  
                result0 = result1; 
            end
        end
        % Determine whether to update the best solution found
        if result0 < min_result  % If the current solution is better, update it
            min_result = result0;  
            best_path = path0;  
        end
    end
    RESULT(iter) = min_result; % Save the smallest result found after the end of this external loop
    T = alpfa*T;   % Temperature drop       
end


disp('The best solution is:'); disp(reshape(best_path,4,n/4))
disp('At this time, the optimal value is:'); disp(min_result)


%% Draw the figure found after each iteration
figure
plot(1:maxgen,RESULT,'b-');
xlabel('Number of iterations');


[~,tmp] = calculate_ans(best_path,mydata)  % ahead~Indicates that the first returned result is not required
toc

That's all) matlab is different when we use it together. You can talk to me in private if you need complete documents.