Overall structure

lingo's code is mainly divided into five parts: predefined, data input, objective function, decision variables and constraints.

Note:
1. lingo code needs to start with model and end with end, but in a simple model, both statements can be omitted.

2. A semicolon in English is required after each line of code.

3. lingo is not case sensitive. There can be more than 8 variable names, but not more than 32. The naming method is the same as that required by other programming languages. It must start with a letter and consist of letters, numbers and underscores. The naming in the code is required to be clear, that is, the meaning represented by this variable can be recognized by seeing the name.

4. Comments in lingo need to use "!", And you also need to add a semicolon at the end.

5. lingo has assumed that all variables are nonnegative when solving the optimization model. If you want to remove the restriction, you need to use the function @ free(x), so that x can get any real number.

6. Each statement of lingo can be labeled, such as [OBJ], so that it will also be output when output, so that we can easily identify the meaning of the output result.

Common symbols and sentences

Logical operator

'''
#not# !  Negates the logical value of the operand;
#eq# !  true if the two operands are equal, otherwise false (equal);
#ne# !  true if the two operators are not equal, otherwise false (not equal);
#gt# !  true if left > right, otherwise false (greater than);
#ge# !  true if left > = right, otherwise false (greater than or equal than);
#lt# !  true if left < right, otherwise false (less than);
#le# !  true if left < = right, otherwise false (less than or equal than);
#and# !  When both parameters are true, it is true, otherwise it is false (and);
#or# !  When both parameters are false, it is false; otherwise, it is true (or); '' '

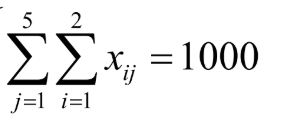
For example, in this case, the range of i itself is 1 ~ 20, and here it needs to be limited to the range of 1 ~ 2:

'''
@sum(link(i,j)|i#le#2:x(i,j))=1000;'''

Relational operator

There are three types of relational operators "=", "< =", "> =". These three operators are mathematical meanings.

Note: in lingo, "<" and ">" mean less than or equal to and greater than or equal to respectively. If strictly less than or strictly greater than is required, for example, a < B, it can be expressed as
A + x < = B, where x is a small positive number, and its value depends on how much a is less than B in the model to meet the requirements.

Mathematical function

There are many mathematical functions. Only a few commonly used ones are listed here. In the actual operation process, if necessary, you can query online by yourself

'''
abs(x) ! return x Absolute value of;
exp(x) ! Return constant e of x Power;
sin(x) ! return x The sine of, x Adopt radian system;
log(x) ! return x Natural logarithm of;
cos(x) ! return x Cosine value of;
lgm(x) ! return x of log Natural logarithm of;
tan(x) ! return x Tangent of;
sign(x) ! If x<0,return-1，Otherwise, return 1;
smax(x1, x2, x3, x4, ...xn) ! return xn Maximum in;
smin(x1, x2, x3, x4, ...xn) ! return xn Minimum value in;
floor(x) ! Round to close to 0;'''

Input and output

1. @ text function: this function is used to decompose the data part and output it to a text file.

'''
@text(['filename'])'''

Filename is the file name, which can be expressed in two ways: relative path and absolute path. If filename is ignored, the data will be output to the standard output device (mostly the screen), and the set to be output is on the right.

Usage example:

model:
sets:
 days/mon..sun/: required,start;
endsets
data:
 !Minimum number of staff required per day;
 required = 20 16 13 16 19 14 12;
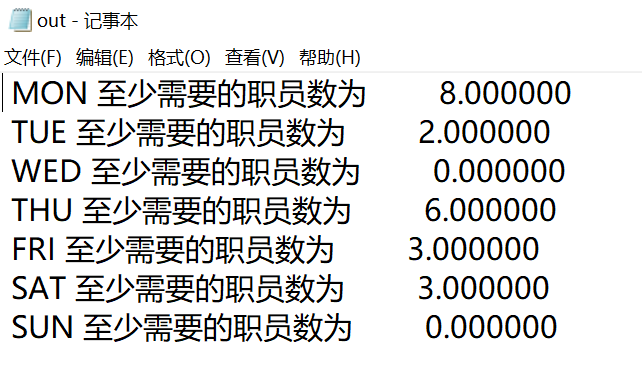
 @text('d:out.txt')=days 'The minimum number of employees required is' start;
enddata
!Minimize the number of employees required per week;
 min=@sum(days: start);
 @for(days(J):
   @sum(days(I) | I #le# 5:
     start(@wrap(J+I+2,7))) >= required(J));
end

Run this code to get the following text file named "out" at the location of lingo

2. @ ole function: interface function for importing or outputting data from excel

'''
x = @ole('Path', 'Name in table');'''

Here we need to talk about the meaning of "name in table". Take excel as an example, select the number to be imported, then click "formula" - "define name", and finally change the name to the name you want. Click name manager to view all names and operate them uniformly.

Usage example:

   x = @OLE('D:/cost.xls',f)

This code means to obtain the data named "f" from the excel table named "cost" in disk D and assign it to x.

Concept of set:

sets:
supply/1..2/:s;
demand/1..3/:d;
link(supply, demand):road, g;
endsets

The initial set is one-dimensional array supply and demand, where the value range is 1 ~ 2 and 1 ~ 3 respectively. Supply and demand are the type name of the array, followed by the variable name.

link: derived set combines the two sets to form a two-dimensional set, which can be understood as a table. For example, the forms of road and g in this question are a table with two rows and three columns.

@sum function

@sum(Array type name(subscript) :  Calculation formula)

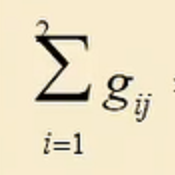
First of all, in the first part, we can know that summation is the evaluation of i, and i is the subscript range of array supply, so

@sum(supply(i) : g(i, j))

Similarly:

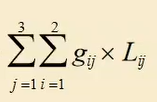
@sum(link(i, j) : g(i, j) * L(i, j))

@for function

@for(Array type name(subscript) : Specific operation)

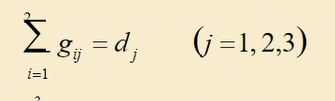
It was difficult for me to understand the meaning of this equation when I first learned it. Now I know it is:

When j = 1, 2 and 3 respectively, make cumulative summation judgment for the case of i = 1 and 2 to meet the equal requirements.

@for(demand(j) : @sum(supply(i) : g(i, j)) = d(j)) 

Operation result analysis

Take this running result as an example

Global optimal solution

The whole code is run twice and the following results are obtained

Objective value

The maximum value of the objective function, that is, the running result is 29000.00

First table

When the values of the two variables are 100.0000 and 30.00000 respectively, the value of the objective function mentioned above is obtained.

Reduced cost: reduced cost coefficient, which indicates the rate of change of the objective function when the variable changes slightly. If it is the optimal solution, it will automatically take zero.

Second table

Slack or Surplus: Slack or Surplus. When the constraint condition is "< =", the difference between the right minus the left is called slack. For the inequality of "> =", the difference between the left minus the right is called surplus. When the left and right sides of the constraint condition are equal, that is, in the ideal state, the value of Slack or Surplus is 0. If the constraint condition cannot be met, the value of Slack or Surplus is 0.

Dual price: shadow price, which indicates the change rate of the objective function when there is a small change in the corresponding constraint.
For example, the second line: because the relaxation or the remaining value is 0, the shadow price is meaningful (if it is not 0, it is not tight in itself. If it is very loose, + 1, - 1 is not necessary). Assuming that the inequality represented by the second line is x2 < = 10, the meaning of shadow price 50 is that if 10 is changed into 11, the result of the objective function will be + 50.