catalogue

Problem overview:

Solution idea:

1. Solve the maximum sub segment sum of one-dimensional matrix

2. Analysis of the maximum field and meaning of the row obtained by adding two adjacent rows

3. Algorithm for solving the maximum sum submatrix problem

Maximum sub segment and solution code:

Maximum submatrix and solution code:

Time complexity analysis:

Problem overview:

Given a matrix, there is a submatrix (which can be empty) to maximize the sum of all numbers of the submatrix. Solve the maximum sum.

Solution idea:

1. Solve the maximum sub segment sum of one-dimensional matrix

We assume that b[j] represents the maximum sum of sub segments ending with a[j]. Under such conditions, we can get the recurrence formula of b[j] as follows:

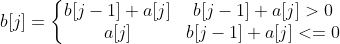
The maximum sub segment sum of the solution we require is the maximum of all b[j] and 0 (take 0 when all numbers in the one-dimensional array are negative).

2. Analysis of the maximum field and meaning of the row obtained by adding two adjacent rows

Assuming that the result obtained by adding the ith row and the I + 1st row of matrix a [] [] is stored in one-dimensional array b [], the j-th element in b [] represents the result of a[i][j]+a[i+1][j]. On this basis, we solve the maximum sub segment and max of b [] array_ Sum, if it is from b[k]~b[m], it means that in the submatrix composed of row I and row J of a [] [] matrix, the row dimension is fixed as the sum of two rows, and the maximum submatrix is a matrix composed of rectangles with a[i][k], a[i][m], a[i+1][k] and a[i+1][m] as vertices, and the sum is max_sum.

3. Algorithm for solving the maximum sum submatrix problem

Based on the above analysis, we can conclude that to solve the maximum submatrix sum problem by using the dynamic programming method, we need to reduce the two-dimensional problem to one-dimensional problem, use an auxiliary matrix to store the sum sequence of rows i to j of a [] [] matrix, and then use the maximum submatrix sum of b [] matrix to solve the maximum submatrix sum of a [].

Maximum sub segment and solution code:

//Parameter Description: n represents the total length of the sequence, and b [] is the given sequence
int max_segment(int n, int b[])
{
    int max_test=0;
    int max_present=0;
    for(int i=0; i<n; i++)
    {
        if(max_test<0) max_test = b[i];
        else max_test += b[i];
        if(max_test>max_present) max_present = max_test;
    }
    return max_present;
}

Maximum submatrix and solution code:

#include <iostream>
using namespace std;
int max_segment(int n, int b[]);
int sum_max(int n, int a[][100]);
int main()
{
    int n, k, max_sum;
    cin>>n;
    int a[10000][10000];
    for(int i=0; i<n; i++)
        for(int j=0; j<n; j++)
            cin>>a[i][j];   //Read in matrix elements
    max_sum=sum_max(n, a);   //Call the function to search the maximum submatrix sum
    cout<<max_sum;

    return 0;
}
//Function: solve the sum of n*n two-dimensional matrix a [] [] and the maximum submatrix
int sum_max(int n, int a[][100])
{
    int b[100];
    int max_t=0;          //Maximum sub segment and
    int max_p=0;          //Maximum submatrix sum up to the current situation
    for(int i=0; i<n; i++)
    {
        for(int k=0; k<n; k++) b[k]=0;
        for(int j=i; j<n; j++)
        {
//Matrix b [] stores the sum sequence of a [] [] matrix from row i to row j
            for(int k=0; k<n; k++)    b[k] += a[j][k];
            max_t=max_segment(n, b);
            if(max_t>max_p) max_p=max_t;
        }
    }
    return max_p;
}
//Function to solve the maximum sub segment sum of one-dimensional matrix b []
int max_segment(int n, int b[])
{
    int max_test=0;
    int max_present=0;
    for(int i=0; i<n; i++)
    {
        if(max_test<0) max_test = b[i];
        else max_test += b[i];
        if(max_test>max_present) max_present = max_test;
    }
    return max_present;
}

Time complexity analysis:

The main part of the algorithm is with sum_ The execution of the max() function. And sum_ The execution of the max function depends on the execution of max_ Multiple calls to the segment() function. For sum_ For the segment() function, we can easily get the time complexity of O(n) (n represents the number of rows and columns of the matrix). On this basis, we can get the calculation method of the time complexity of sum_max() function as follows:

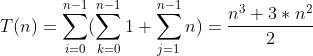
Therefore, the overall time complexity of the algorithm is 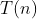~.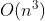