Basic introduction to merging and sorting

Merge sort is a sort method based on the idea of merging. The algorithm adopts the classical divide and conquer strategy

Divide and conquer divides the problem into some small problems and then solves them recursively, while the conquer stage "fixes" the answers obtained in different stages, that is, divide and conquer

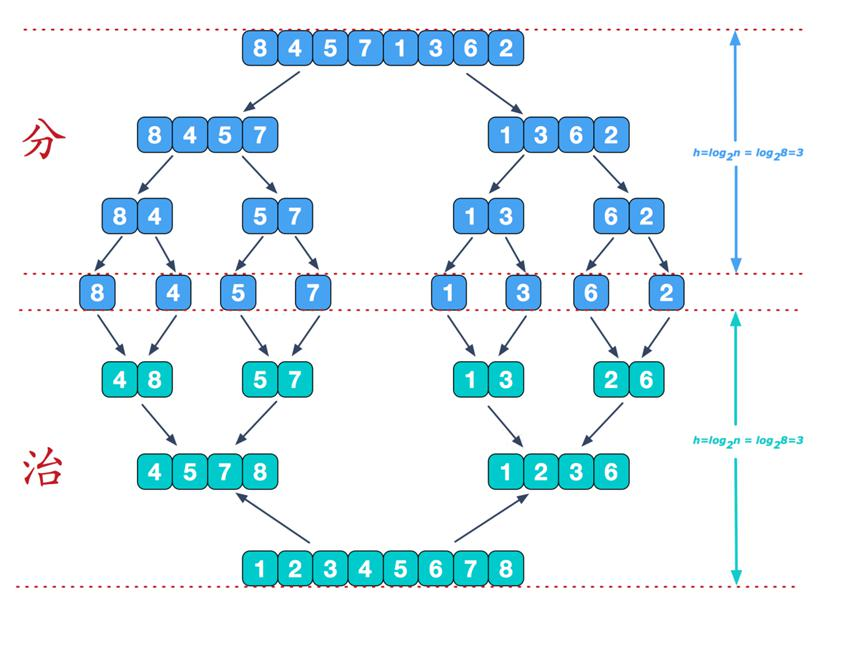
Merging and sorting thought

Sub -- > treatment

Merge sort code idea

When merging, we actually merge two adjacent sub arrays (arr1 and arr2) in the original array (ARR). We use three pointers to represent the position of the two sub arrays in the original array

arr[left] ~ arr[mid] is arr1

arr[mid + 1] ~ arr[right] is arr2

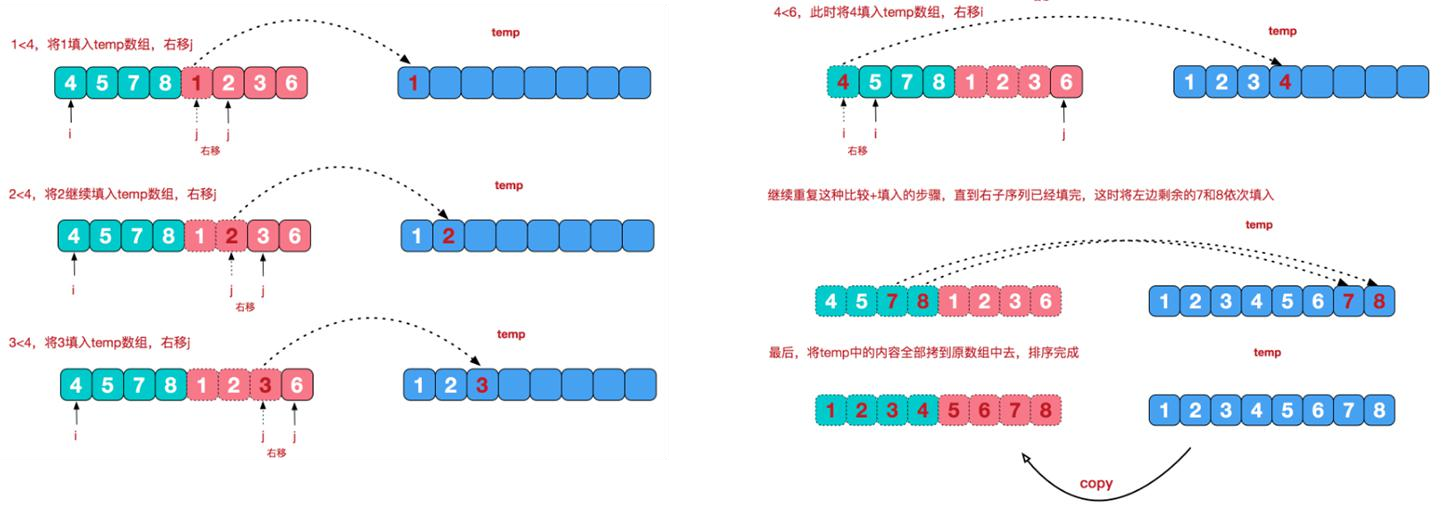
How to merge?

First, you need a temporary temp array with the same size as the original array arr

Define auxiliary pointer i to traverse arr1 and auxiliary pointer j to traverse arr2. The principle is to put the numbers in arr1 and arr2 into temp so that temp[left] ~ temp[right] are ordered arrays

Finally, copy the data in the temp temporary array back to the original array (personally, it's OK to copy it back next time...)

How to divide?

Left recursive splitting: mergeSort(arr, left, mid, temp);

Right recursive splitting: mergeSort(arr, mid + 1, right, temp);

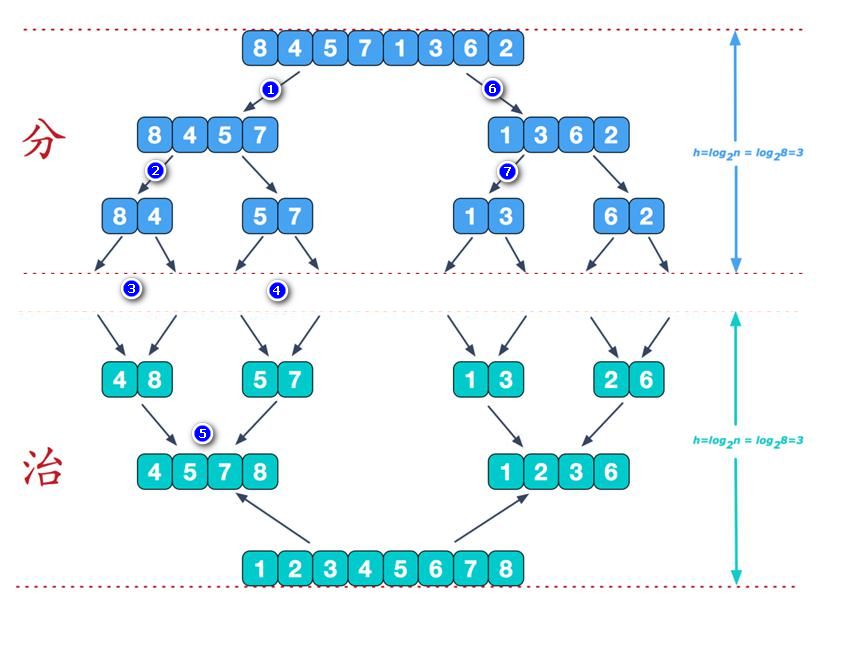
summary

First divide the array into left and right halves, and first perform left half recursion:

First, execute left recursion to the deepest layer. If the condition if (left < right) is not satisfied, start merging, merge {8,4} into the temporary array temp, change it into an ordered array {4,8}, and then copy it back to the original array arr

Then, execute the deepest right recursion. If the condition if (left < right) is not satisfied, start merging, merge {5,7} into the temporary array temp, change it into an ordered array {2,7}, and then copy it back to the original array arr

After merging, recursively backtrack to the previous section and start merging. Merge {4,5,7,8} into the temporary array temp, change it into an ordered array {4,5,7,8}, and then copy it back to the original array arr

The same is true for recursion on the right and left sides

The code is as follows:

 // Opening + closing method
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (left + right) / 2; // Intermediate index
            // Decompose recursively to the left
            mergeSort(arr, left, mid, temp);
            // Decompose recursively to the right
            mergeSort(arr, mid + 1, right, temp);
            // merge
            merge(arr, left, mid, right, temp);
        }
    }

    // Merging method
    /**
     *
     * @param arr Sorted original array
     * @param left Initial index of left ordered sequence
     * @param mid Intermediate index
     * @param right Right index
     * @param temp Array for transit
     */
    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {

        int i = left; // Initialization i, the initial index of the left ordered sequence
        int j = mid + 1; // Initialization j, the initial index of the ordered sequence on the right
        int t = 0; // Points to the current index of the temp array

        // (I)
        // First, fill the left and right (ordered) data into the temp array according to the rules
        // Until one side of the ordered sequence on the left and right is processed
        while (i <= mid && j <= right) {// continue
            // If the current element of the left ordered sequence is less than or equal to the current element of the right ordered sequence
            // Fill the current element on the left into the temp array
            // Then t++, i++
            if (arr[i] <= arr[j]) {
                temp[t] = arr[i];
                t += 1;
                i += 1;
            } else { // On the contrary, fill the current element of the ordered sequence on the right into the temp array
                temp[t] = arr[j];
                t += 1;
                j += 1;
            }
        }

        // (II)
        // Fill all the data on the side with remaining data into temp in turn
        while (i <= mid) { // The ordered sequence on the left and the remaining elements are filled into temp
            temp[t] = arr[i];
            t += 1;
            i += 1;
        }

        while (j <= right) { // The ordered sequence on the right and the remaining elements are filled into temp
            temp[t] = arr[j];
            t += 1;
            j += 1;
        }

        // (III)
        // Copy the elements of temp array to arr
        // Note that not all are copied every time
        t = 0;
        int tempLeft = left; //
        // The first time: templeft = 0, right = 1 / / the second time: templeft = 2, right = 3 / / the third time: TL = 0, RI = 3
        // Last tempLeft = 0 right = 7
        while (tempLeft <= right) {
            arr[tempLeft] = temp[t];
            t += 1;
            tempLeft += 1;
        }

    }