The method calls itself and passes in different variables each time (helps to solve complex problems and make the code concise)
Important rules:
1. When a method is executed, a new protected space (stack space) will be created
2. The local variables of the method are independent and will not affect each other
3. If the reference data type (array, object) is used in the method, the data of the reference type will be shared
[if it is a reference data type, the formal parameters passed in the method are addresses, and these formal parameters can affect the same space in the heap through this address]
4. Recursion must approach the condition of exiting recursion, otherwise infinite recursion [stack overflow error]
5. After a method is executed or encounters a return, it will return (the result will be returned to the person who calls it). After the method is executed or encounters a return, the method will end

Every time recursion is required, a new stack will appear, and the old stack will not be executed until the new stack is executed (so the first output result is the result of the latest stack, and so on)

Suppose the following method is changed:

After modification, only one n=2 will appear in the result
why?( When the outermost layer [layer 1] method is executed, it meets n > 2, so recursion is executed (the output statements in else are not executed), and when the second layer recursion also meets n > 2, so the third layer recursion is executed... And so on. Recursion is executed until n=2 does not meet n > 2. At this time, the output statements in else are executed, and n=2 is output, Because the previous layers of recursion execute the next layer of recursion, n=3, 4, 5 and 6 will not appear... (in case of)
Factorial
//Factorial
public int factorical(int n){
if(n == 1){
return 1;
}else{
return factorical(n - 1)*n;
}
}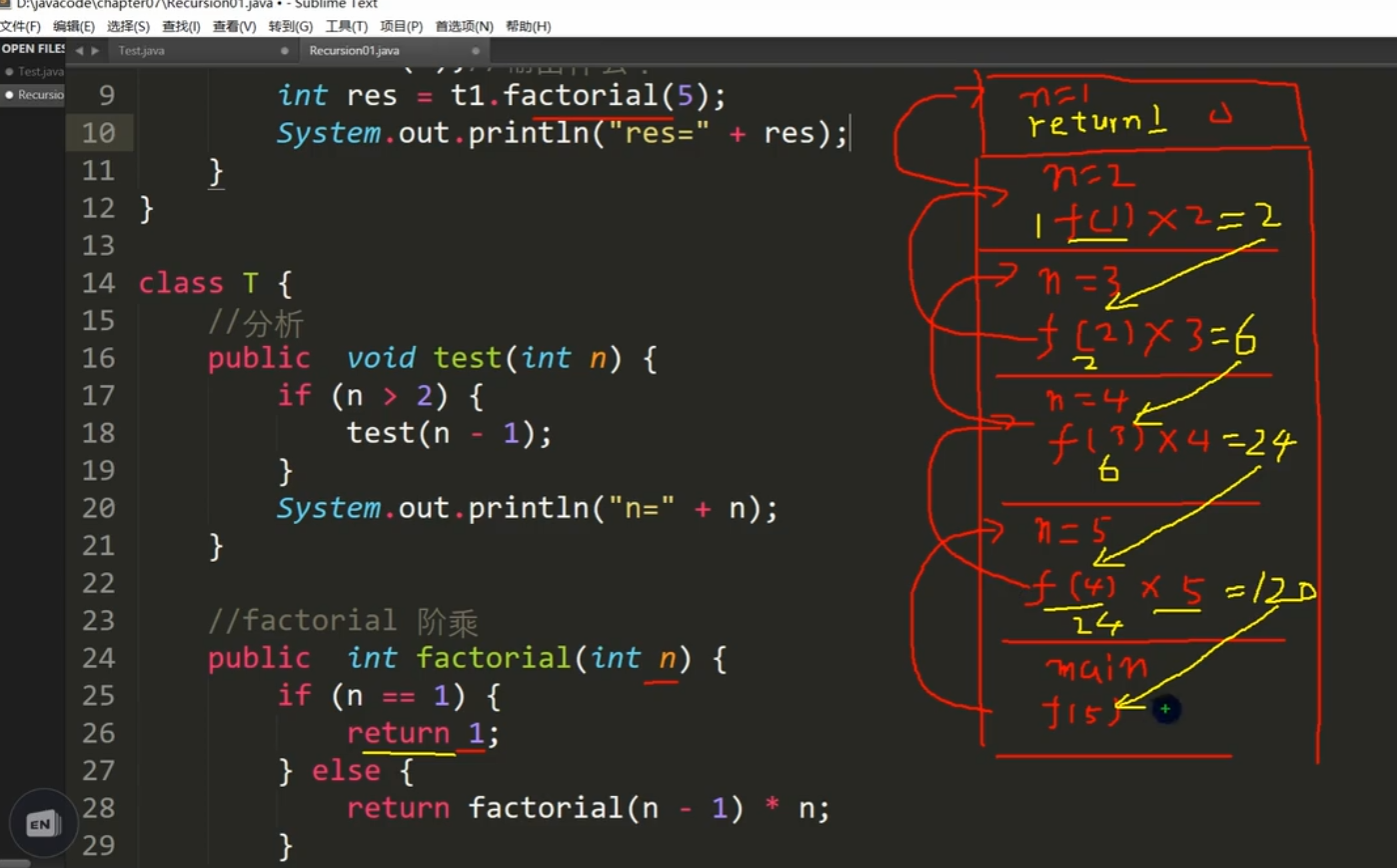
The determined value obtained from the topmost stack goes down in sequence, 5 * 4 * 3 * 2 * 1 = 120
practice:
① Fibonacci number (the last number is the sum of the first two numbers)
class t{
public int feibo(int n){
if(n==1 || n ==2){
return 1
}else{
return feibo(n-1)+feibo(n-2);
}
}
}It can be improved slightly (for data protection)
class t{
public int feibo(int n){
if(n>0){
if(n==1 || n ==2){
return 1;
}else{
return feibo(n-1)+feibo(n-2);
}
}else{
System.out.println("Please enter a number greater than 0");
return -1;
}
}
}② Monkeys eat peaches: there is a pile of peaches. Monkeys eat half of them on the first day and eat one more! After that, monkeys eat half of them every day, and then eat one more. When you want to eat again on the 10th day (i.e. you haven't eaten yet), you find that there is only one peach. Question: how many peaches were there in the beginning?
(rule: number of peaches in the previous day = number of peaches in the next day + 1 * 2)
//Monkeys eat peaches
public int tao(int day){//Day stands for the penultimate day
if(day==1){
return 1;
}else{
return (tao(day-1)+1)*2;
}
}Method 2:
public int tao2(int day){//Day is the day of a positive number
if(day == 10){
return 1;
}else if(day >=1 && day <= 9){
return (tao2(day + 1)+1)*2;
}else{
return -1;
}
}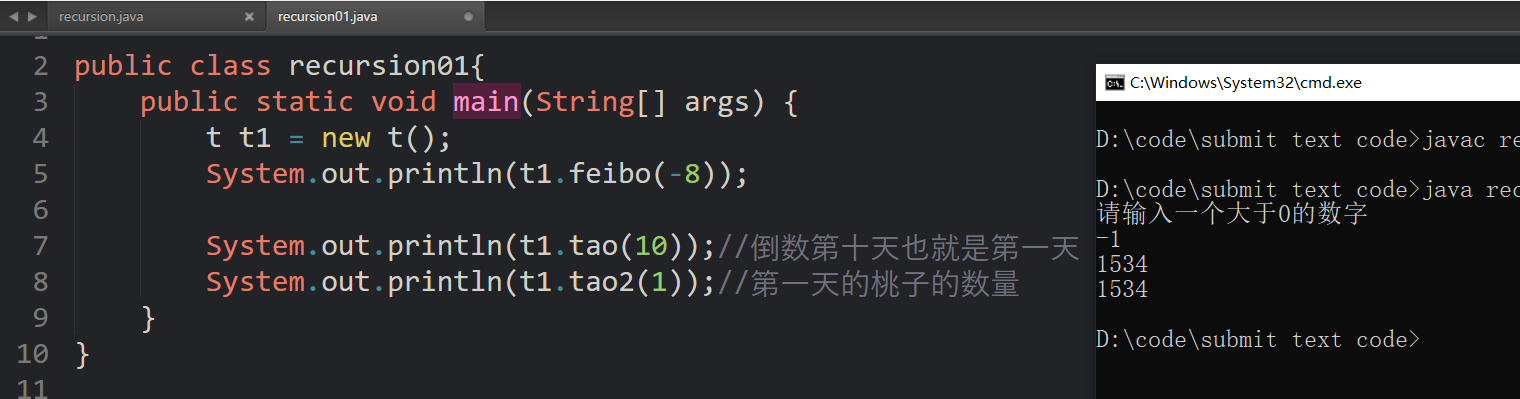
The result is 1534, both methods are OK (the important thing is to find the law)
Maze problem (the ball goes from the upper left corner to the upper right corner to avoid obstacles)

public class migong{
public static void main(String[] args) {
//Using two-dimensional array to represent maze
//The element value 0 can walk, and 1 represents an obstacle
int[][] map = new int[8][7];//Maze of 8 rows and 7 columns
//Set both the top and bottom lines to 1 (indicating that you can't go)
for(int i = 0;i<7;i++){
map[0][i] = 1;
map[7][i] = 1;
}
//Set the left and right columns as 1 (each column has 8 rows, so I < 8)
for(int i = 0;i<8;i++){
map[i][0] = 1;
map[i][6] = 1;
}
//Set two obstacles separately
map[3][1] = 1;
map[3][2] = 1;
//Output current map
System.out.println("Current map situation:");
for(int i = 0;i<map.length;i++){//The length of a two-dimensional array is the number of rows
for(int j = 0;j<map[i].length;j++){
System.out.print(map[i][j]+" ");
}
System.out.println();
}
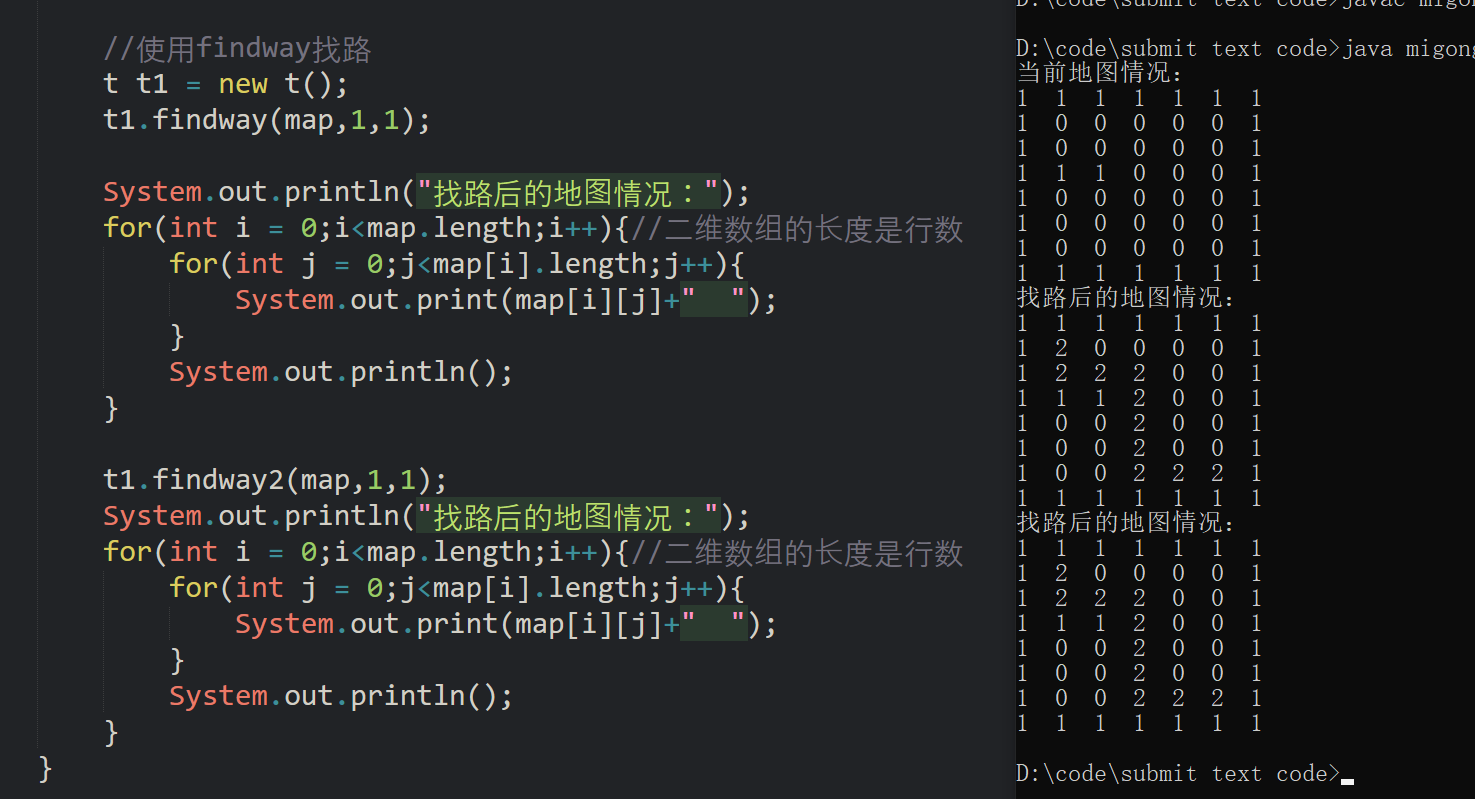
//Find the way with findway
t t1 = new t();
t1.findway(map,1,1);
System.out.println("Map after road finding:");
for(int i = 0;i<map.length;i++){//The length of a two-dimensional array is the number of rows
for(int j = 0;j<map[i].length;j++){
System.out.print(map[i][j]+" ");
}
System.out.println();
}
}
}
class t{
//Recursive thinking solution
//findway this method is used to find the maze path
//Returns true if found, false if not found
//map is a two-dimensional array that represents a maze
//i. j represents the position, and the initial position is (1, 1)
//Specify the meaning of the array value. The element value 0 can walk, 1 represents an obstacle, 2 can walk, and 3 can walk but can't walk
//When map[6][5] = 2, you have found the way, otherwise continue to find
//Determine the route finding strategy, bottom - > right - > Top - > left
public boolean findway(int[][] map,int i,int j){
if (map[6][5] == 2) {//It means finding the way
return true;
}else{
if(map[i][j] == 0){//It means that this position can go
//Suppose it can go through
map[i][j] = 2;
//Use the policy to determine whether it can really go through (lower right, upper left)
if(findway(map,i + 1,j)){//Go down first
return true;
}else if(findway(map,i,j + 1)){//Go right
return true;
}else if(findway(map,i - 1,j)){//take
return true;
}else if(findway(map,i,j - 1)){//Go left
return true;
}else{
map[i][j] = 3;//, assuming it can go through, it can't go through, so it's assigned a value of 3
return false;
}
}else{
return false;
}
}
}
}

(in the result, 2 is the path of the ball)
In the findway method, when we pass in the array, i and j, all the elements in the array are 0 except the two also defined elements in the periphery and inside are 1. At this time, map[6][5] is not equal to 2. At this time, we enter the following else. When we call the method, the i and j passed in are 1. At this time, map[1][1] = 0 is established. When we enter the if statement, we first assume that it can go through, First change the current position to 2, and then let him go down (this so-called going down is actually to use recursion to call his method again, but change the passed parameter to an element below the starting position), and then look at the element to meet the condition in if else. If you can't go down, go right... And so on, Until the end position becomes 2 or returns false

Why does calling two different methods produce the same result?
 Which method to call first? The following method is the same as the above method?
Which method to call first? The following method is the same as the above method?
Test backtracking phenomenon

Backtracking: for example, block the lower right corner of the starting position. When the ball goes below the starting position in the order of lower, right, upper and left, it is found that it is impossible to go in the order of lower, lower, right, upper and left. At this time, the position will become 3. At this time, it will return to the starting position. After returning to the starting position, it will be found that it is impossible to go below the starting position, so it will go to the right [ When the four directions of a certain position fail to go, it will return to the previous stack and detect according to the next direction of the direction that has just gone.]