Several bosses of Microsoft and Google organized an interview question brushing group, which can add administrator VX: sxxzs3998 (note CSDN) to participate in discussion and live broadcast

1. Title

Give you an array of routes that represent a series of bus lines, where each route [i] represents a bus line on which the ith bus will cycle.

For example, route routes[0] = [1, 5, 7] means that the 0th bus will always follow the station route of sequence 1 - > 5 - > 7 - > 1 - > 5 - > 7 - > 1 - >. Now start from source station (not on the bus at the beginning) and go to target station. During this period, you can only take the bus.

Find the minimum number of buses to take. If it is impossible to reach the terminal station, return to - 1.

Example 1:
Input: routes = [[1,2,7],[3,6,7]], source = 1, target = 6
 Output: 2
 Explanation: the best strategy is to take the first bus to station 7 , Then transfer to the second bus to station 6. 

Example 2:
Input: routes = [[7,12],[4,5,15],[6],[15,19],[9,12,13]], source = 15, target = 12
 Output:-1

2. Analysis

The following figure is the construction form of the example graph. The adjacency table is used to represent the neighbor nodes of the graph, and different colors represent different buses.

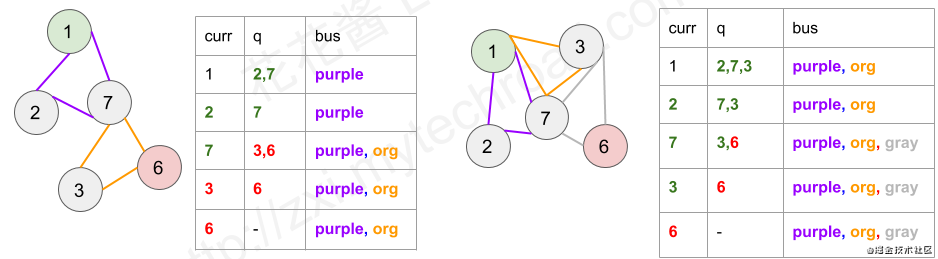
First of all, we don't care about the station. We only care about the bus route. We can regard each line as a point. For any two lines, if the stations they pass through intersect, then connect an edge between the two points to form a graph. Is this reminiscent of DFS or BFS?

Some points (alignments) in the diagram contain starting points S S S, we take them as the starting point. Some points (alignments) contain endpoints T T T, we take them as the end.

Then the problem is transformed into finding the shortest path from the beginning to the end. Because there may be more than one start point and end point, we create two new nodes. One start point is used to point to all included nodes S S The point of S, an end point, is used to point to all containing T T Point of T. Next, the problem becomes the single source shortest path problem.

Since it is to find the shortest distance, we should first consider BFS. The pseudo code is as follows

int numBusesToDestination(vector<vector<int>>& routes, int source, int target) {
    queue<Node> q;
    vector<bool> visited;
    q.push(Starting point route);
    while (!q.empty()) {
        Take out a node;
        Judge whether it has been visited;
        Set access;
        Judge whether it is the end point. If so, return to the answer.
        for (All nodes associated with this node) {
            if(This node has not been accessed) {
                q.push(This node);
            }
        }
    }
    return -1;
}

We should find all the routes through a site. As long as we pass through the same site, these routes are connected. Therefore, use unordered_ Map < int, vector > stationtoroute to store the data of all routes passing through the site. key represents the site and value represents all routes passing through the site. Traverse all routes and record the routes passing through the same site.

unordered_map<int, vector<int> > stationToRoute;
for (int i = 0; i < routes.size(); i++) {
    for (int j = 0; j < routes[i].size(); j++) {
        stationToRoute[routes[i][j]].push_back(i);
    }
}

Next, through this data structure, we build our graph. Traverse all key s in the hash table and connect all routes in a value.

for (auto &p : stationToRoute) {
    for (auto &route : p.second) {
        for (auto &secondRoute : p.second) {
            if (secondRoute != route) {
                routeToRoutes[route].push_back(secondRoute);
            }   
        }
    }
}

We can also find all start routes and end routes through stationToRoute[source] and stationToRoute[target]. Finally, we can record the route and the number of routes we have passed through at the same time through the method of queue < pair < int, int > >.

To sum up, the code is as follows:

class Solution {
public:
    int numBusesToDestination(vector<vector<int>>& routes, int source, int target) {
        // There will be XX who can't get on the bus The beginning is the end
        if (source == target) {return 0;}
        // First traverse the stations in all routes and record the routes that each station can pass
        unordered_map<int, vector<int> > stationToRoute;
        for (int i = 0; i < routes.size(); i++) {
            for (int j = 0; j < routes[i].size(); j++) {
                stationToRoute[routes[i][j]].push_back(i);
            }
        }
        // Then traverse all platforms and establish the relationship between routes according to the routes passed by the platforms
        vector<vector<int> > routeToRoutes(500, vector<int>(0));
        for (auto &p : stationToRoute) {
            for (auto &route : p.second) {
                for (auto &secondRoute : p.second) {
                    if (secondRoute != route) {
                        routeToRoutes[route].push_back(secondRoute);
                    }   
                }
            }
        }

        unordered_set<int> endRoutes;
        for (auto &route : stationToRoute[target]) {
            endRoutes.insert(route);
        }

        vector<bool> visited(500, false);

        // First, there must be a queue to archive node s and some information
        // < which route, how many cars have you been on >
        queue<pair<int, int> > q;
        for (auto &route : stationToRoute[source]) {
            q.push({route, 0});
        }
        while (!q.empty()) {
        // Take out the queue element
            auto tmp = q.front();
            q.pop();
        // If yes, continue;
        // Set visited again
            if(visited[tmp.first]) {
                continue;
            }
        // I haven't visited, just see if it's the end
            visited[tmp.first] = true;
            if (endRoutes.find(tmp.first) != endRoutes.end()) {
                return tmp.second + 1;
            }
            for (auto &route : routeToRoutes[tmp.first]) {
                // Enter queue for all next possible
                if (!visited[route]) {
                    q.push({route, tmp.second + 1});
                }
            }
        }
        return -1;
    }
};

Complexity analysis:

• Time complexity: suppose the number of routes is N N N. Each route has a maximum of M M M stations. Then the sorting complexity is O ( N M l o g M ) O(NMlogM) O(NMlogM), the drawing complexity is O ( N 2 M ) O(N^2M) O(N2M), BFS complexity is O(N^2). Therefore, the total time complexity is after ignoring the low-order term O ( N 2 M ) O(N^2M) O(N2M).
• Space complexity: O ( N 2 ) O(N^2) O(N2)

Several bosses of Microsoft and Google organized an interview question brushing group, which can add administrator VX: sxxzs3998 (note CSDN) to participate in discussion and live broadcast