There are two minimum spanning tree algorithms. One is prim algorithm and the other is Kruskal algorithm. The time complexity of the two algorithms are o (n^2) and O (mlogn) [n is the number of points and m is the number of edges]. The two algorithms behave differently in different graphs.

Let's start with prim algorithm.

The core idea of this algorithm is to divide the points into two sets a and B. A is the set of selected points and B is the set of unselected points.

Go through n cycles, find the nearest point of the connected graph composed of the selected set in the unselected set each time, put it into the selected set, and update other points with this point;

The idea is very similar to dijestra algorithm. Here are the code and comments.

 

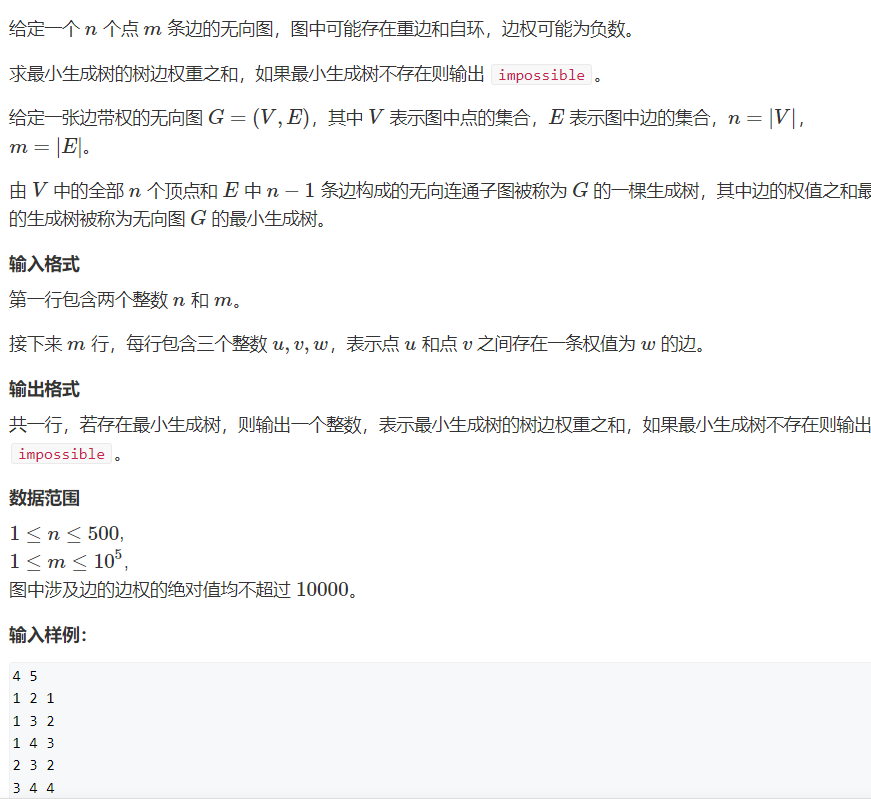
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N = 510;

int g[N][N];//Storing graphs with adjacency matrix
int dist[N];//dist[i] represents the shortest distance from point I to the connected block composed of the selected set points
int st[N];//st[i]=1 means that point I is set a and = 0 is set B
int n, m;

int prim() {

	//The initialization distance from each point to A set is infinite, and the starting point is point 1, so dist[1]=0;
	memset(dist, 0x3f, sizeof dist);
	dist[1] = 0;

	int res = 0;//res is the weight of set A

	for (int i = 0; i < n; i++) {

		int t = -1;

		for (int j = 1; j <= n; j++) {//Search for selectable points in set B

			if (!st[j] && (t == -1 || dist[t] > dist[j]))
				t = j;

		}

		st[t] = 1;//Mark this point into set A

		for (int j = 1; j <= n; j++) {//Update other points with this point

			dist[j] = min(dist[j], g[t][j]);

		}
		res += dist[t];//Update weight

	}
	if (res >= 0x3f3f3f) return 0;
	else return res;

}


int main() {

	cin >> n >> m;

	memset(g, 0x3f, sizeof g);

	for (int i = 0; i < m; i++) {//receive data 

		int a, b, c; cin >> a >> b >> c;
		if (a != b)
			g[a][b] = g[b][a] = min(g[a][b], c);

	}

	int t = prim();
	if (!t) cout << "impossible";
	else cout << t;

}

Then there is Kruskal algorithm, which uses the knowledge of parallel search set.

The specific ideas are as follows

First sort all the edges according to the weight, and then increase by 1~n, and then traverse all the edges by 1~n. if the two points of an edge do not belong to the same set, then merge the sets of the two points and calculate the weight.

Because it is sorted, the result is the minimum spanning tree

The specific codes and notes are as follows;

 

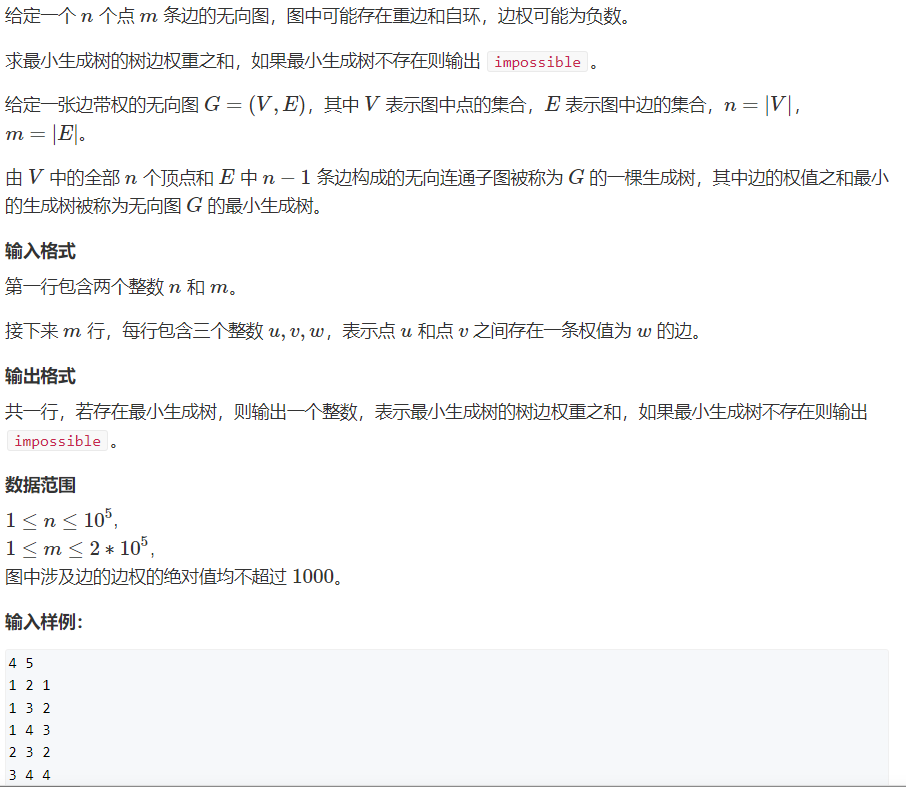
#include<iostream>
#include<algorithm>
using namespace std;

const int N = 200020;

struct edge {//Store all edges in one structure

	int a, b, w;

	bool operator< (const edge W)const {//Heavy load<

		return w < W.w;

	}

}edges[N];

int n, m;
int p[N];

int find(int x) {//The core code of the parallel search set. Those who do not know the parallel search set can turn to the introduction of the parallel search set I originally wrote

	if (p[x] != x) p[x] = find(p[x]);
	return p[x];

}


int main() {

	cin >> n >> m;


	for (int i = 0; i < m; i++) {//Receive all edges

		int a, b, c; scanf("%d%d%d", &a, &b, &c);

		edges[i].a = a, edges[i].b = b, edges[i].w = c;

	}

	sort(edges, edges + m);

	for (int i = 1; i <= n; i++) p[i] = i;

	int res = 0, cont = 0;//res is the weight sum of all sets, and cont is the number of points of all sets [excluding the set with only one point]

	for (int i = 0; i < m; i++) {

		int a = edges[i].a, b = edges[i].b, w = edges[i].w;

		int ka = find(a), kb = find(b);//Find the set of these two points

		if (ka != kb) {

			res += w;
			p[ka] = kb;
			cont++;
		}

	}

	if (cont < n - 1) cout << "impossible";
	else cout << res;
}

Then there are two algorithms of bipartite graph, one is the coloring method, and the other is the Hungarian algorithm. The former is to judge whether a graph is a bipartite graph, and the role of the other algorithm is difficult to express. I will explain it with a question.

Let's first talk about the dyeing method. Its core is dfs algorithm. The idea is as follows;

Select a point in a connection block as the starting point, then dye it black, find the sub node of this point, dye it all white, then enter the sub point, find all the sub points of the sub point, dye it black, and repeat the operation of black and white. If there is no conflict, the figure is a bipartite graph, If and only if there is a ring with cardinal number of edges in the graph, there is a conflict, that is, when a child point is found, the color of the child point is the same as that of the parent point;

The specific codes are as follows:;

 

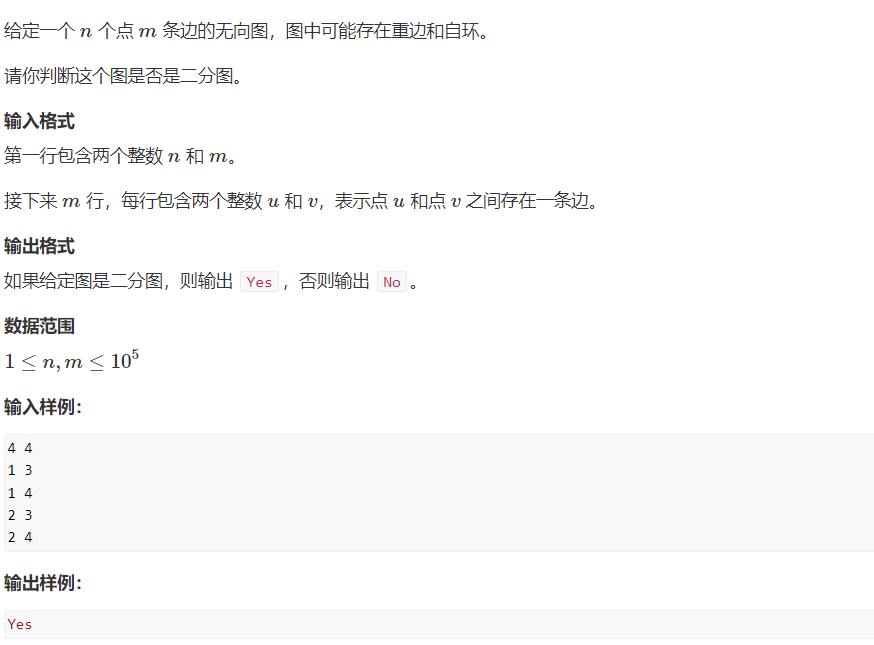
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

const int N = 100010;

vector<vector<int>> ve(N);//Storing graphs with vector

int n, m;

int col[N];//Point I is black when col[i]=1, white when col[i]=2, and colorless when col[i]=0;

bool dfs(int x, int c) {

	col[x] = c;

	for (int i = 0; i < ve[x].size(); i++) {//Dye all the child points in a different color from the parent point

		if (!col[ve[x][i]]) {

			if (!dfs(ve[x][i], 3 - c))
				return 0;


		}
		else if (col[ve[x][i]] == c) return 0;//If the child point has a color, judge whether it is the same color as the husband node


	}

	return 1;
}

int main() {

	cin >> n >> m;

	for (int i = 1; i <= m; i++) {//Receiving diagram

		int a, b; scanf("%d%d", &a, &b);
		ve[a].push_back(b);
		ve[b].push_back(a);

	}

	int flag = 1;

	for (int i = 1; i <= n; i++) {//Dyeing

		if (!col[i]) {

			if (!dfs(i, 1)) {//When dfs=0, it indicates that there is a conflict, and the graph is not a bipartite graph
				flag = 0;
				break;
			}

		}

	}

	if (!flag) cout << "No";
	else cout << "Yes";

}