3, Program code

(1)MinWeigh

package maxweightminvalue;

import java.util.Scanner;

public class MinWeight {
        private int coinSort;//Types of coins
        private int e;//Weight of the piggy bank
        private int f;//The piggy bank is full of the maximum weight
        private int v;//Capacity of the piggy bank
        private int[] dp=new int[10001];//dp array
        Coin[] coins;//An array of denominations and weights of coins

        public void inputData() {
            int exit = 1;
            Scanner scanner = new Scanner(System.in);
            //System.out.println("please enter the number of tests:");
            while (exit==1) {
                    coins = new Coin[1000];
                    System.out.println("Please enter the weight of the piggy bank and the maximum weight filled:");
                    e = scanner.nextInt();
                    f = scanner.nextInt();
                    v = f - e;
                    System.out.println("Please enter the type of coin:");
                    coinSort = scanner.nextInt();
                    System.out.println("Please enter the face value and weight of each coin:");
                    for (int i = 0; i < coinSort; i++) {
                        coins[i] = new Coin();
                        coins[i].value = scanner.nextInt();
                        coins[i].weight = scanner.nextInt();
                    }
                display();
                System.out.println("Do you want to continue the test (enter 1 to continue the test, enter 0 to exit):");
                exit=scanner.nextInt();
            }
        }

        public int load(){
            dp[0]=0;
            for(int i=1;i<=v;i++){
                dp[i]=500000001;//Set the maximum value that can be set in the array to facilitate comparison and filtering out the minimum value
            }
            for(int i=0;i<coinSort;i++){
                for(int j=0;j<=v;j++){
                    if (j-coins[i].weight<0)
                        dp[j]=dp[j];//There is no change because it can't fit
                    else//If it can be loaded, it is necessary to compare the minimum value of the loaded items
                        dp[j]=Math.min(dp[j],dp[j-coins[i].weight]+coins[i].value);//State transition equation
                }
            }
            return dp[v];
        }

        public void display(){
                if(load()!=500000001){
                    System.out.println("What is the minimum amount in the piggy bank"+load());
                }
                else {//If the last value of the array does not change, it indicates that the current gold coin type does not match the gold coin quality
                    System.out.println("It's impossible");
                }
        }



    }

(2)Coin

package maxweightminvalue;

public class Coin {
    public int value;
    public int weight;
    public int number;
}

(3)TestMinWeight

package test;

import maxweightminvalue.MinWeight;

public class TestMinWeight {
    public static void main(String[] args) {
        MinWeight minWeight =new MinWeight();
        minWeight.inputData();
    }
}

4, Experimental results (including screenshots of program operation)

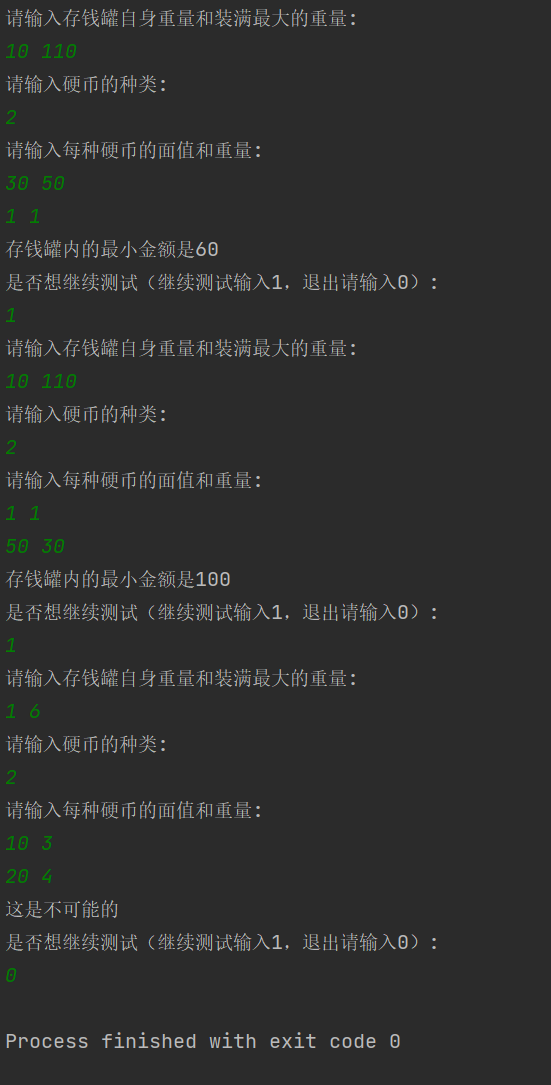
5, Problems and Solutions

This experiment is a complete knapsack problem. Different from 01 knapsack, one item can be put into more than one item, so we need to consider the quantity of the item when reloading the item. Under normal circumstances, it is to find the maximum value that can be loaded into the knapsack, but this problem is the minimum value, so it is difficult to find the state transition equation again, and it is difficult to consider the idea when solving the array , I started to work after referring to the ideas on the Internet. Here are the points different from the maximum value:

(1) At the beginning, different from other knapsack problems to solve the maximum value, it is to initialize the dp array with a value of 0, but copy each element in the dp array into the maximum value that the integer variable can bear.

for(int i=1;i<=v;i++){
    dp[i]=500000001; / / set the maximum value that can be set in the array to facilitate comparison and filter out the minimum value
}

Because the minimum value needs to be filtered out, the comparison error is caused by the influence of the initialization of the original array and the stored data when the value is assigned to other minimum values.

(2) Solving state transition equation

        There are many methods to solve the equation of state on the Internet, such as adding a k variable corresponding to the number of items in the · cycle of ij for recording, but it is suitable for the maximum value but not for the minimum value, so there are many problems. When modifying, we can't simply change the maximum value to the minimum value. Therefore, after searching the data, we found the following equation of state:

dp[j]=Math.min(dp[j],dp[j-coins[i].weight]+coins[i].value); / / state transition equation

        The state transition equation is the coin type and quality given by the cyclic solution, and the smaller one is stored. Moreover, a coin is compared once, but the final results are stored in the one-dimensional dp array. Finally, cycle to the last value. If the storage tank can be filled exactly, the last value of the dp array is not 500000000 1. If it can not be filled, the last dp number If the value of the group is still 5000000001 and there is no change, the given coin type cannot fill the volume, so it is impossible.

6, Experimental experience

The experience of this experiment is that the algorithm should expand its own ideas, have its own thinking process, and strive to come up with a good algorithm one day.

  The first blog does have the component of checking information on the Internet. If you have any questions, please leave a message in the comment area. I also want to learn some good ideas~