In the last article, we said that single-layer perceptron realizes simple logic circuit and multi-layer perceptron realizes XOR gate circuit. Threshold is introduced θ， Offset b. Now, according to the expression in the previous article, the reality activation function.

The expression of our previous perceptron is as follows:

y = {
x1w1+x2w2+b >0 return 1
x1w1+x2w2+b <=0 return 0
}

Now, let's make the whole of x1w1+x2w2+b equal to α， Now there is a special mapping relationship when α＞ When 0, make h( α)= 1. When α<= When 0, make h( α)= 0 H here( α) Functions are called activation functions. The activation function is a function that converts the input sum into the output value. Therefore, the expression can be written as y = H( α).

The advantage of perceptron is that it can express complex functions or logical operations. However, it has some defects. For example, the weight w needs to be set manually, and the offset b also needs to be set manually. It can not automatically optimize the weight and offset through a certain set of specific rules. Therefore, the emergence of neural network can deal with this problem, because the weight of neural network can be adjusted automatically. Neural network is similar to perceptron because it also has input layer, middle layer (hidden layer) and output layer. The activation function used by neural network does not belong to step function (step function: set a threshold and output when the input exceeds the threshold). Common activation function: sigmoid function: H( α)= 1 / (1+e^(-x)).

Implementation of step function:

import numpy as np
import matplotlib.pyplot as plt


"""

#encoding="utf-8"
@Author:Mr.Pan_Academic mania
@finish_time:2022/2/10
 Comparison between the step function of perceptron and the activation function of neural network
"""

def JY(inx):
    if inx > 0:
        return 1
    else:
        return 0

def JY2(inx):
    shape_tup = inx.shape
    print(shape_tup[0])
    if len(shape_tup) > 1:#matrix
        for vector in inx:
            for num in range(shape_tup[1]):
                if vector[num] > 0:
                    vector[num] = 1
                else:
                    vector[num] = 0
    else:#vector
        for n in range(shape_tup[0]):
            if inx[n] > 0:
                inx[n] = 1
            else:
                inx[n] = 0
    return inx

def JY3(inx):
    return np.array(
        inx > 0,dtype=np.int
    )



def sigmoid():
    pass

if __name__ == '__main__':
    print(JY(0.5))
    print(JY2(np.array([-0.2,0.3,-1])))
    print(JY2(np.array([[-0.5,0.5,1],[1,2,0],[0.2,-3,0.01],[-6,2,-0.9],[1,-2,6],[-0.3,0,1]])))
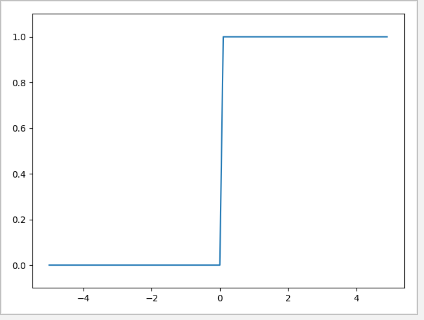
    x = np.arange(-5.0, 5.0, 0.1)
    y = JY3(inx=x)
    plt.plot(x,y)
    plt.ylim(-0.1,1.1)
    plt.show()

Operation results:


Implementation of sigmoid function:

def sigmoid(inx):
    return 1 / (1 + np.exp(-inx))

However, we note that the activation function can allow the input value to be vector or matrix type data. Unlike step functions, only one data type of input can be specified.
Test sigmoid function:

X = np.array([-1,0,1,2])
X2 = np.array([[-0.5,-1,0],[1,2,-2]])
X3 = 1
print(sigmoid(X))
print(sigmoid(X2))
print(sigmoid(X3))

Operation results:

Drawing code:

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(inx=x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()

sigmoid function image:

Comparing the step function and activation function images, we can see that the sigmoid function image changes more gently and the step function changes more violently. Sigmoid changes continuously with the change of input and output. Sigmoid function is obviously more suitable for observing small changes in values.

Sigmoid function is the same as step function in that when the input is small, the output is close to 0. When the input is large, the output is close to 1. No matter how large or small the input data is, the output result is always within (0,1). Both step function and sigmoid are nonlinear functions.

The activation of neural network must use nonlinear function. The reason is that the use of linear function will make the stack meaningless. For example: g(x)=Cx(C is constant), g(x) is a linear function. Then, after 3 times of superposition, G (g (g(x)) = cccx. In fact, it is equivalent to h (x) = C ^ 3 * x (linear function), and there is no difference. Therefore, we need to use nonlinear function as the activation function of neural network.

Finally, thank you for coming to watch my article. There may be many deficiencies in the article. I also hope to point out and forgive you.