968. Monitoring binary tree
Link to force buckle topic: https://leetcode-cn.com/problems/binary-tree-cameras
Given a binary tree, we install cameras on the nodes of the tree.
Each camera head on a node can monitor its parent, itself, and its immediate children.
Calculate the minimum number of cameras required for all nodes of the monitoring tree.
Example 1:

- Input: [0,0,null,0,0]
- Output: 1
- Explanation: as shown in the figure, one camera is enough to monitor all nodes.
Example 2:
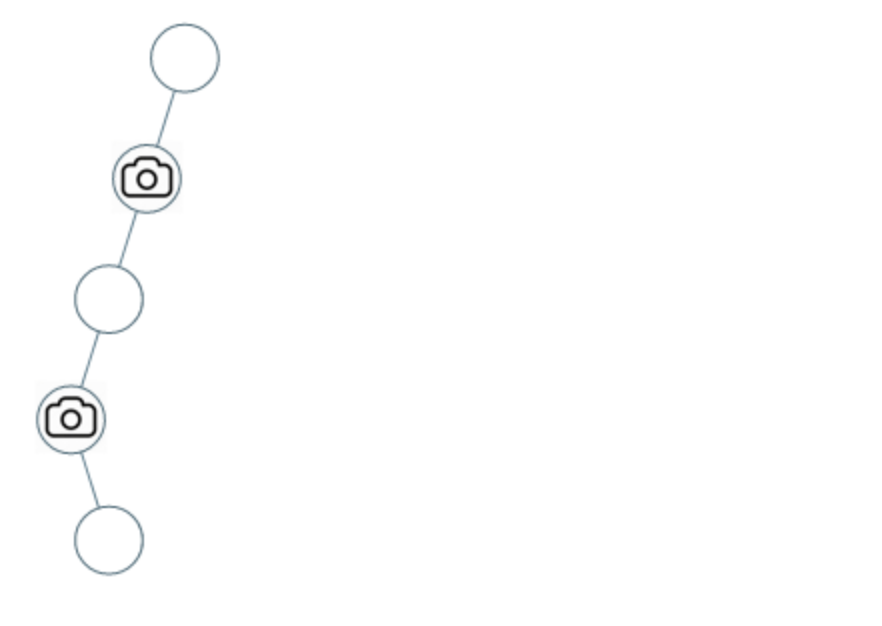
- Input: [0,0,null,0,null,0,null,null,0]
- Output: 2
- Explanation: at least two cameras are required to monitor all nodes of the tree. The figure above shows one of the effective locations where the camera is placed.
Tips:
- The range of nodes in a given tree is [1, 1000].
- The value of each node is 0.
thinking
First of all, how to place the camera to make it the smallest?
In fact, we can get inspiration from the example in the title. We found that the cameras in the example in the title are not placed on the leaf node!
This is a very important clue. The camera can cover the upper, middle and lower layers. If the camera is placed on the leaf node, it will waste one layer of coverage.
Therefore, only by placing the camera at the parent node of the leaf node can we make full use of the coverage area of the camera.
Then some students may ask, why not start from the node? Why should we look from the leaf node?
Because if the head node does not put the camera, it saves a camera. If the leaf node does not put the camera, the number of cameras saved is exponential.
Therefore, we should look from bottom to top, local optimization: let the parent node of the leaf node install cameras, use the least cameras, and overall optimization: use the least number of all cameras!
Local optimization deduces global optimization. If you can't find a counterexample, follow greed!
At this time, the general idea is to put a camera on the parent node of the leaf node from low to top, and then put a camera every two nodes until it reaches the head node of the binary tree.
At this time, there are two difficulties in this topic:
- Traversal of binary tree
- How to place a camera every two nodes
Determine traversal order
How to deduce from low up in binary tree?
You can use post order traversal, that is, the order in the left and right, so that you can deduce from bottom to top in the process of backtracking.
The post order traversal code is as follows:
int traversal(TreeNode* cur) {
// Empty node, which has coverage
if (Termination conditions) return ;
int left = traversal(cur->left); // Left
int right = traversal(cur->right); // right
Logical processing // in
return ;
}
Note that in the above code, we take the return value of the left child and the return value of the right child, that is, left and right, and then deduce the state of the intermediate node
How to place a camera every two nodes
At this time, the state transition formula is required. We should not mix it with the dynamic state transition formula. There is no optimization process for the state transition of this problem, which is a simple state transition!
Let's see how this state should be transferred. First, let's see how many states each node may have:
There are three types:
- This node has no overrides
- This node has cameras
- This node has overrides
We have three numbers:
- 0: this node has no overrides
- 1: This node has cameras
- 2: This node has overrides
You should not find the state of the fourth node.
Some students may wonder if there is a fourth state: there is no camera on this node. In fact, no camera means no coverage or coverage, so there are still three states in total.
Because in the process of traversing the tree, empty nodes will be encountered, so the problem comes. What kind of state is an empty node? Empty node means no coverage? Means there's a camera? Or is there coverage?
Return to the essence. In order to minimize the number of cameras, we should try to make the parent node of the leaf node install cameras, so as to minimize the number of cameras.
Then, the empty node cannot be in the state of no coverage, so that the leaf node will put the camera, and the empty node cannot be in the state of having the camera, so that the parent node of the leaf node does not need to put the camera, but can put the camera on the grandfather node of the leaf node.
Therefore, the status of an empty node can only be overwritten, so you can put a camera on the parent node of the leaf node
The next step is recursion.
Then the termination condition of recursion should be that an empty node is encountered, and 2 (with coverage) should be returned. The reason has been explained above.
The code is as follows:
// Empty node, which has coverage if (cur == NULL) return 2;
Recursive functions and termination conditions have been determined. Let's look at single-layer logic processing.
There are four main situations:
- Case 1: both left and right nodes are covered
If the left child has coverage and the right child has coverage, the intermediate node should be in the state of no coverage.
As shown in the figure:
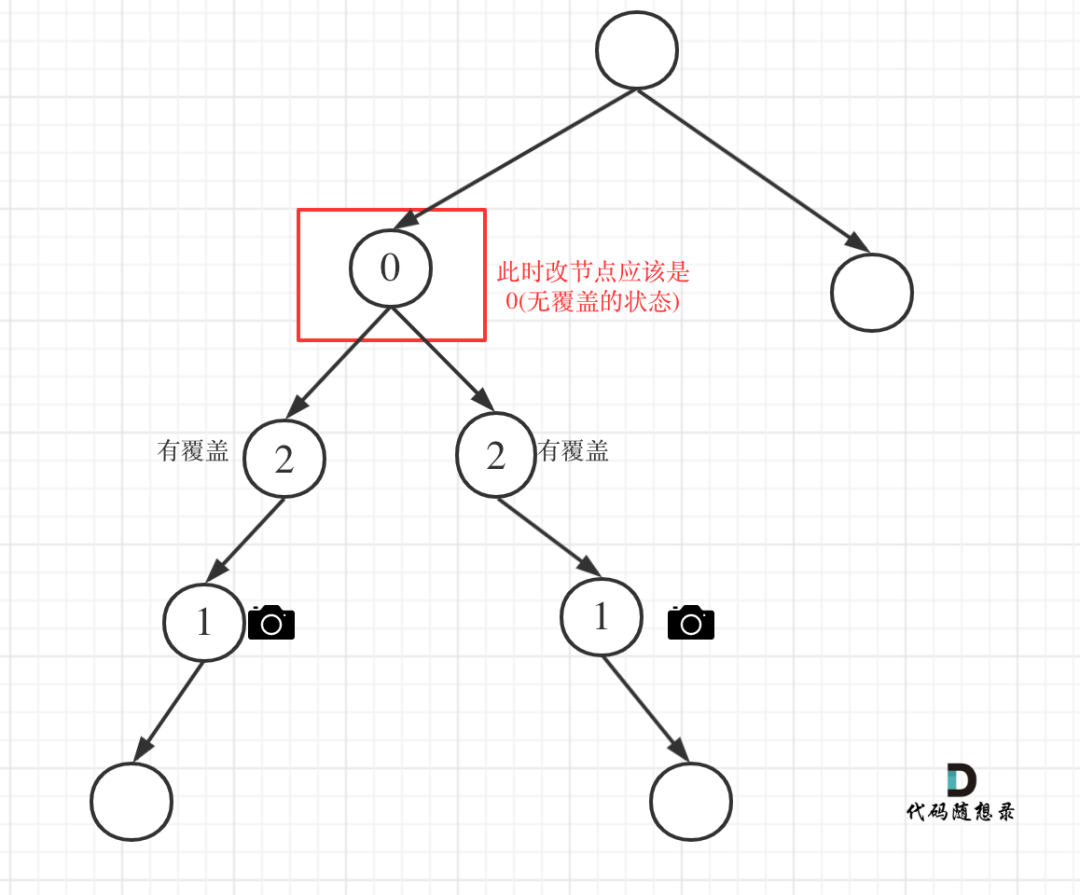
968. Monitoring binary tree 2
The code is as follows:
// Both left and right nodes are covered if (left == 2 && right == 2) return 0;
- Case 2: at least one of the left and right nodes has no coverage
The intermediate node (parent node) should place the camera if:
Left = = 0 & & right = = 0 left = = 1 & & right = = 0 left node has camera, right node has no coverage left = = 0 & & right = = 1 left node has no coverage, right node has camera left = = 0 & & right = = 2 left node has no coverage, right node has coverage left = = 2 & & right = = 0 left node has coverage, right node has no coverage
This is not difficult to understand. After all, if a child is not covered, the parent node should put the camera.
At this time, the number of cameras should be increased by one, and return 1 means that the intermediate node places cameras.
The code is as follows:
if (left == 0 || right == 0) {
result++;
return 1;
}
- Case 3: at least one of the left and right nodes has a camera
In the following cases, if one of the left and right child nodes has a camera, its parent node should be 2 (covered state)
Left = = 1 & & right = = 2 the left node has cameras and the right node has coverage left = = 2 & & right = = 1 the left node has coverage and the right node has cameras left = = 1 & & right = = 1 both left and right nodes have cameras
The code is as follows:
if (left == 1 || right == 1) return 2;
From this code, we can see that what if left = = 1 and right = = 0? In fact, this condition has been judged in case 2, as shown in the figure:
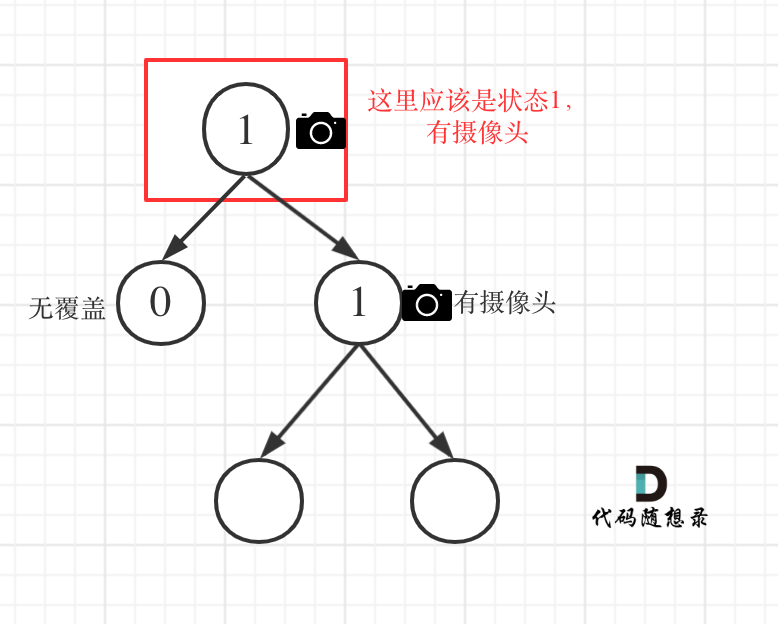
968. Monitoring binary tree 1
This situation is also easily confused by most students.
- Case 4: the header node is not covered
After all the above processing, after the recursion, the header node may have no coverage, as shown in the figure:
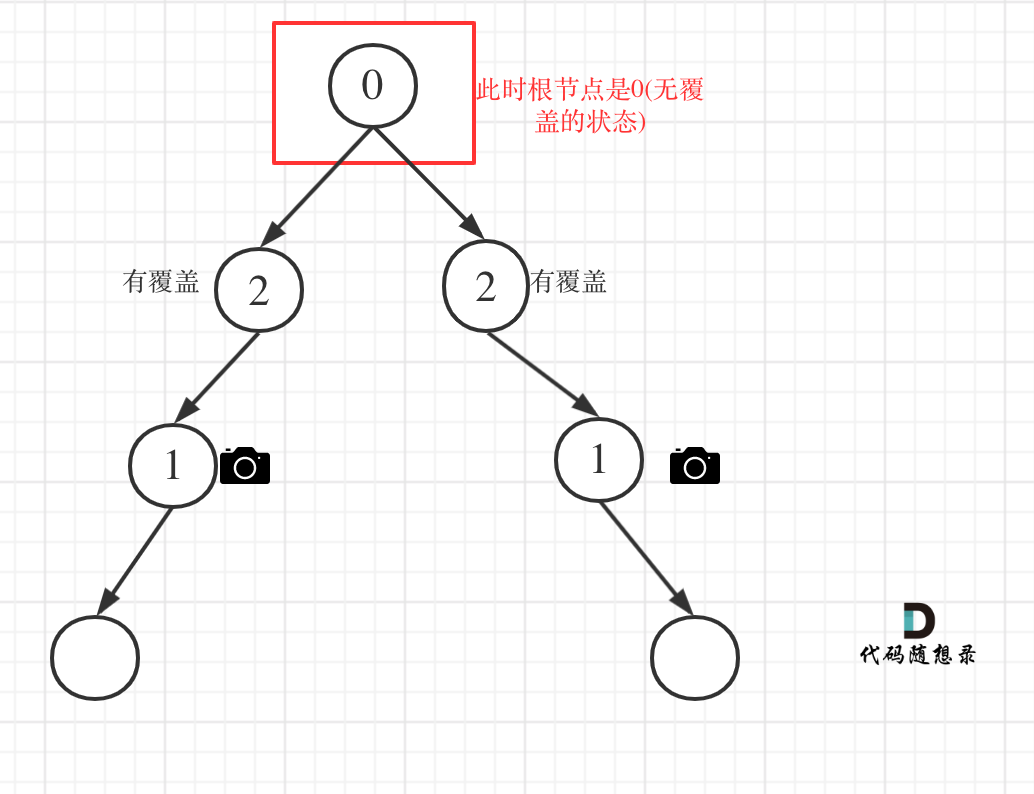
968. Monitoring binary tree 3
Therefore, after the recursion, the root node must be judged. If it is not covered, result + +, the code is as follows:
int minCameraCover(TreeNode* root) {
result = 0;
if (traversal(root) == 0) { // root no overwrite
result++;
}
return result;
}
After analyzing the above four cases, the code is almost the same. The overall code is as follows:
(my code comments below are very detailed. In order to clarify the situation, I specially list each situation.)
The C + + code is as follows:
// Version one
class Solution {
private:
int result;
int traversal(TreeNode* cur) {
// Empty node, which has coverage
if (cur == NULL) return 2;
int left = traversal(cur->left); // Left
int right = traversal(cur->right); // right
// Case 1
// Both left and right nodes are covered
if (left == 2 && right == 2) return 0;
// Case 2
// Left = = 0 & & right = = no coverage for nodes around 0
// Left = = 1 & & right = = 0 the left node has a camera and the right node has no coverage
// Left = = 0 & & right = = 1 whether the left node is covered, and whether the right node is covered
// Left = = 0 & & right = = 2 left node not covered, right node covered
// Left = = 2 & & right = = 0 the left node is covered, and the right node is not covered
if (left == 0 || right == 0) {
result++;
return 1;
}
// Case 3
// Left = = 1 & & right = = 2 the left node has a camera and the right node has coverage
// Left = = 2 & & right = = 1 left node has coverage and right node has camera
// Left = = 1 & & right = = 1 there are cameras on both left and right nodes
// In other cases, the previous code has been overwritten
if (left == 1 || right == 1) return 2;
// I didn't use else in the above code, mainly to show each branch condition, so that the code is helpful for readers to understand
// This return -1 logic will not come here.
return -1;
}
public:
int minCameraCover(TreeNode* root) {
result = 0;
// Situation 4
if (traversal(root) == 0) { // root no overwrite
result++;
}
return result;
}
};
On the basis of the above codes, the codes are simplified as follows:
// Version 2
class Solution {
private:
int result;
int traversal(TreeNode* cur) {
if (cur == NULL) return 2;
int left = traversal(cur->left); // Left
int right = traversal(cur->right); // right
if (left == 2 && right == 2) return 0;
else if (left == 0 || right == 0) {
result++;
return 1;
} else return 2;
}
public:
int minCameraCover(TreeNode* root) {
result = 0;
if (traversal(root) == 0) { // root no overwrite
result++;
}
return result;
}
};
You may be surprised that it can be so brief. In fact, on the basis of version 1, use else to directly cover some situations.
On the Internet, you can find a lot of this God level code, but it is not clear. If you look at the code directly, the more you see, the more dizzy you are specified. Therefore, it is recommended that you look at the code of version 1 step by step. Version 2 is useless!.
summary
The difficulty of this problem is to think of greedy ideas first, and then traversal and state derivation.
In fact, it is difficult to deduce the state on the binary tree. You need to be very skilled in the operation of the binary tree.
This topic is a real hard, everyone feel, ha ha.
Other language versions
Java
class Solution {
private int count = 0;
public int minCameraCover(TreeNode root) {
if (trval(root) == 0) count++;
return count;
}
private int trval(TreeNode root) {
if (root == null) return -1;
int left = trval(root.left);
int right = trval(root.right);
if (left == 0 || right == 0) {
count++;
return 2;
}
if (left == 2 || right == 2) {
return 1;
}
return 0;
}
}
Python
class Solution:
def minCameraCover(self, root: TreeNode) -> int:
# Greedy Algo:
# Install cameras from bottom to top: skip leaves to minimize the number of installations, local optimization - > global optimization
# First install the parent node of leaves, and then install a camera every two layers of nodes until Head
# 0: the node is not overwritten
# 1: This node has cameras
# 2: This node has overrides
result = 0
# Traversal from bottom to top: post order (left and right middle)
def traversal(curr: TreeNode) -> int:
nonlocal result
if not curr: return 2
left = traversal(curr.left)
right = traversal(curr.right)
# Case 1:
# Both left and right nodes are covered
if left == 2 and right == 2:
return 0
# Case 2:
# Left = = 0 & & right = = no coverage for nodes around 0
# Left = = 1 & & right = = 0 the left node has a camera and the right node has no coverage
# Left = = 0 & & right = = 1 whether the left node is covered, and whether the right node is covered
# Left = = 0 & & right = = 2 left node not covered, right node covered
# Left = = 2 & & right = = 0 the left node is covered, and the right node is not covered
elif left == 0 or right == 0:
result += 1
return 1
# Case 3:
# Left = = 1 & & right = = 2 the left node has a camera and the right node has coverage
# Left = = 2 & & right = = 1 left node has coverage and right node has camera
# Left = = 1 & & right = = 1 there are cameras on both left and right nodes
elif left == 1 or right == 1:
return 2
# In other cases, the previous code has been overwritten
if traversal(root) == 0:
result += 1
return result
Go
const inf = math.MaxInt64 / 2
func minCameraCover(root *TreeNode) int {
var dfs func(*TreeNode) (a, b, c int)
dfs = func(node *TreeNode) (a, b, c int) {
if node == nil {
return inf, 0, 0
}
lefta, leftb, leftc := dfs(node.Left)
righta, rightb, rightc := dfs(node.Right)
a = leftc + rightc + 1
b = min(a, min(lefta+rightb, righta+leftb))
c = min(a, leftb+rightb)
return
}
_, ans, _ := dfs(root)
return ans
}
func min(a, b int) int {
if a <= b {
return a
}
return b
}
Javascript
var minCameraCover = function(root) {
let result = 0
function traversal(cur) {
if(cur === null) {
return 2
}
let left = traversal(cur.left)
let right = traversal(cur.right)
if(left === 2 && right === 2) {
return 0
}
if(left === 0 || right === 0) {
result++
return 1
}
if(left === 1 || right === 1) {
return 2
}
return -1
}
if(traversal(root) === 0) {
result++
}
return result
};
C
/*
**Function traverses the binary tree. When judging the state of a node, judge according to the state of its left and right child nodes
**Status: 0 is not covered by the camera. 1. Camera shall be set at this node. 2 this node has been covered by the camera
*/
int traversal(struct TreeNode* node, int* ans) {
//Recursive end condition: the incoming node is NULL, assuming that this node can be covered by the camera. In this way, it is convenient to judge the leaf node and set the leaf node to 0
if(!node)
return 2;
//After traversing the binary tree, record the state of left and right children. Update the node status according to the left and right child status
int left = traversal(node->left, ans);
int right = traversal(node->right, ans);
//If both left and right children can be covered by the camera, set the father node status to 0
if(left == 2 && right == 2) {
return 0;
}
//If the status of one node of the left and right children is not covered (0), set the parent node status to camera
if(left == 0 || right == 0) {
(*ans)++;
return 1;
}
//If the left and right children have a camera, it proves that the father node can be covered. Change the parent node status to 2
if(left == 1 || right == 1)
return 2;
//The logic will not go to - 1 and the statement will not be executed
return -1;
}
int minCameraCover(struct TreeNode* root){
int ans = 0;
//After traversing the whole binary tree. The head node may not be covered. At this time, if the return value of the function is 0, it proves that the head node is not covered. It shows that the head node also needs to add cameras, ans++
if(traversal(root, &ans) == 0)
ans++;
return ans;
}