motor drive is a very common application. In many systems, we will encounter the need to change the motor speed to achieve the corresponding control function, which involves the problem of motor speed curve planning. In this article, we will briefly discuss the problem of S-curve planning of motor.

1. Basic principles

   S-type speed curve control algorithm is another commonly used acceleration and deceleration control strategy in the field of industrial control. S-type curve well overcomes the problem of discontinuous acceleration of T-type curve.

   S-shaped curve is actually a T-shaped change process of acceleration. Specifically, it is a process of increasing acceleration, constant acceleration and reducing speed. In the whole speed regulation procedure, the acceleration changes continuously, and the change reflected in the speed is a smooth S-shaped curve. As shown in the figure below:

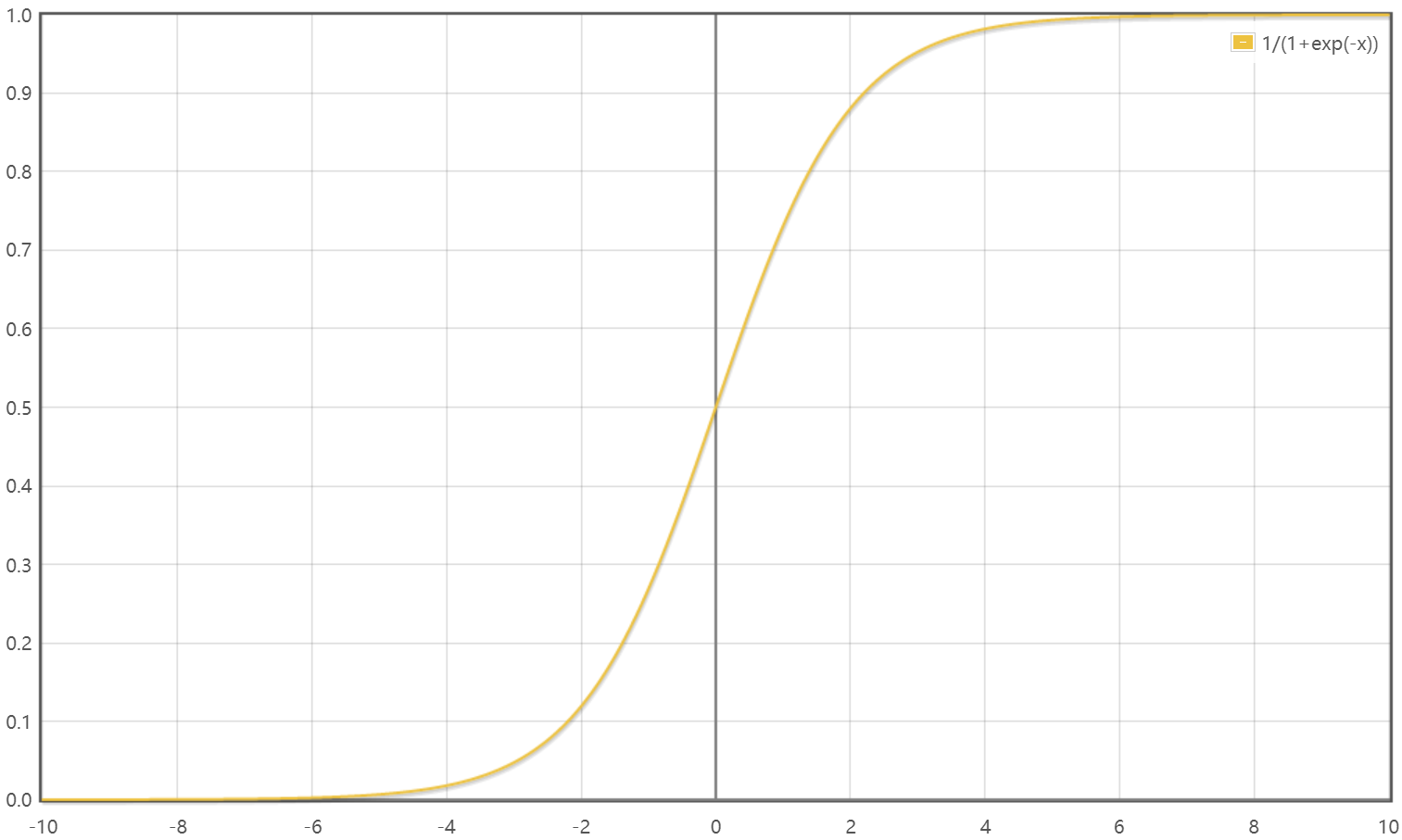
   this is a common form of S curve, and its function expression is as follows:

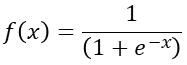
  this function is a special case of this kind of function, which is not universal. In our application, we may need to translate or stretch the S-shaped curve in the horizontal axis and vertical axis according to the requirements of the application. Therefore, the more general description of this function is as follows:

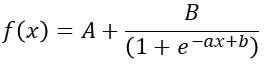
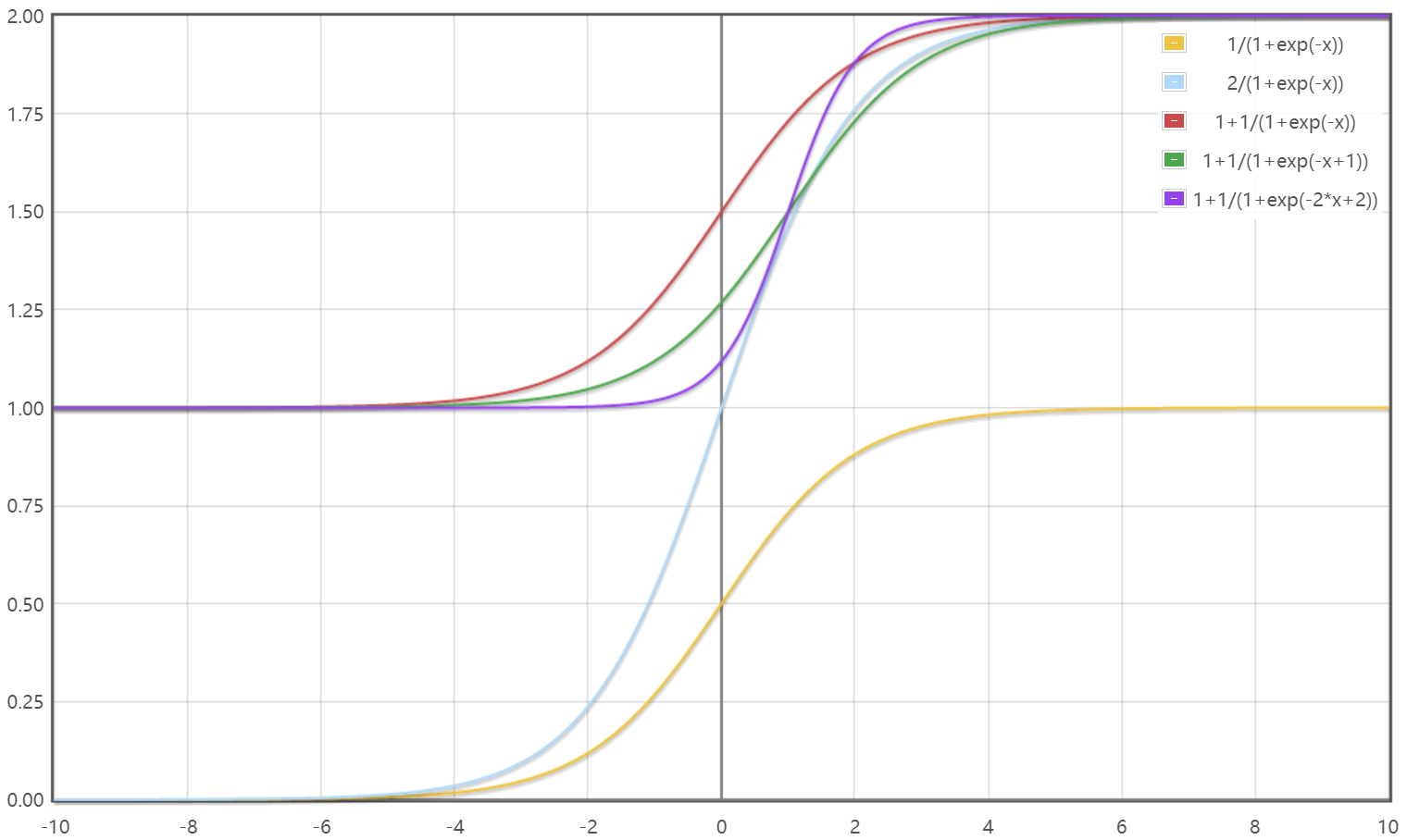
   in this expression, a represents the translation in the longitudinal axis direction, B represents the stretching in the longitudinal axis direction, a represents the stretching in the transverse axis direction, and B represents the translation in the transverse axis direction. Specifically reflected in the function graph is as shown in the figure below:

  so how to use this S-curve function to speed the motor? We consider that the so-called motor speed regulation actually means that there is a certain functional relationship between motor speed and running time. Obviously, the vertical axis is the motor speed and the horizontal axis is the running time. Therefore, we can get the functional relationship of the S-type speed curve of the motor as follows:

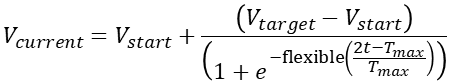
  you may find that the function of this velocity curve seems to be slightly different from the previous mathematical function. This is to better adapt to the difference of speed regulation. Mathematically, the number axes are symmetrical, but in the process of speed adjustment, there can be no negative number in speed and time, so we need to translate it. However, after translation, the graph of S curve is asymmetric, so we take the middle point of the speed regulation time of the whole speed regulation process as the axis, which is symmetrical, so we have the above function expression.

2. Design and Implementation

  we have briefly described the mathematical principle and application expression of S-type speed planning curve. Next, let's consider how to implement it.

  considering that there may be multiple speed planning curves in the same drive due to the needs of application scenarios. Therefore, we consider it based on the idea of object, so that we only need to replace different curves when replacing different curves. So let's first analyze the attributes and operations of curve objects.

   in view of the previous analysis, we believe that as a speed regulation curve object, we should at least record the initial speed, current speed, target speed, acceleration, maximum speed, minimum speed, speed regulation time, speed regulation time span, curve type and S curve stretch at the beginning of speed regulation. We record these as the attributes of the object. Based on this, we can define the object type of motor speed curve as:

/* Define motor speed curve object */
typedef struct CurveObject {
  float startSpeed;    //Initial speed at start of speed regulation
  float currentSpeed;   //Current speed
  float targetSpeed;   //Target speed
  float stepSpeed;    //acceleration
  float speedMax;     //Maximum speed
  float speedMin;     //Minimum speed
  uint32_t aTimes;    //Speed regulation time
  uint32_t maxTimes;   //Speed regulating span
  SpeedCurveType curveMode;  //Curve type
  float flexible;     //S-curve stretch
}CurveObjectType;

  we have defined a speed curve object type. Next, let's analyze how to realize an S-type speed regulation curve. We have described that speed is actually a function of time. According to the functional expression of speed and time analyzed earlier, we realize the following:

void (*pCalCurve[])(CurveObjectType *curve)={CalCurveNone,CalCurveTRAP,CalCurveSPTA};
 
/* Motor curve acceleration and deceleration operation-------------------------------------------------------- */
void MotorVelocityCurve(CurveObjectType *curve)
{
  float temp=0;
  
  if(curve->targetSpeed>curve->speedMax)
  {
     curve->targetSpeed=curve->speedMax;
  }
  
  if(curve->targetSpeed<curve->speedMin)
  {
     curve->targetSpeed=curve->speedMin;
  }
 
  if((fabs(curve->currentSpeed-curve->startSpeed)<=curve->stepSpeed)&&(curve->maxTimes==0))
  {
     if(curve->startSpeed<curve->speedMin)
     {
       curve->startSpeed=curve->speedMin;
     }
     
     temp=fabs(curve->targetSpeed-curve->startSpeed);
     temp=temp/curve->stepSpeed;
     curve->maxTimes=(uint32_t)(temp)+1;
     curve->aTimes=0;
  }
  
  if(curve->aTimes<curve->maxTimes)
  {
     pCalCurve[curve->curveMode](curve);
     curve->aTimes++;
  }
  else
  {
     curve->currentSpeed=curve->targetSpeed;
     curve->maxTimes=0;
     curve->aTimes=0;
  }
}
 
/*S Curve velocity calculation*/
static void CalCurveSPTA(CurveObjectType *spta)
{
  float power=0.0;
  float speed=0.0;
  
  power=(2*((float)spta->aTimes)-((float)spta->maxTimes))/((float)spta->maxTimes);
  power=(0.0-spta->flexible)*power;
  
  speed=1+expf(power);
  speed=(spta->targetSpeed-spta->startSpeed)/speed;
  spta->currentSpeed=speed+spta->startSpeed;
  
  if(spta->currentSpeed>spta->speedMax)
  {
     spta->currentSpeed=spta->speedMax;
  }
  
  if(spta->currentSpeed<spta->speedMin)
  {
     spta->currentSpeed=spta->speedMin;
  }
}

    in this implementation, we integrate the same operations of various curves for more general practicability, and then integrate their different parts in the form of callback functions through curve type attributes.

3. Application and verification

  we have realized the basic design and implementation of the speed planning curve of S-type motor. Next, we use this speed regulation curve to realize an example of motor speed regulation. When we define the speed planning curve, we implement it with the idea of and object, so we first specify a curve object instance.

  CurveObjectType curve; // Motor speed regulation curve

    after declaring this curve object, we need to initialize and assign it to use it correctly. Most attributes can be given initial values directly according to the requirements of the application object. Note the attribute of curve type, which will determine what kind of speed planning curve to use. This attribute is the SpeedCurveType enumeration, which is defined as follows:

/* Enumeration defining motor speed curve types */
typedef enum SpeedCurve {
  CURVE_NONE=0,  //Zhiqi
  CURVE_TRAP=1,  //Trapezoidal curve
  CURVE_SPTA=2  //S-shaped curve
}SpeedCurveType;

  here, we need to initialize the curve type as a T-shaped speed planning curve. The specific operations are as follows:

  curve.curveMode=CURVE_SPTA;

   after initialization, the curve object can be used to adjust the motor speed. It is also very simple to use. As long as we call the MotorVelocityCurve function implemented earlier according to a certain time cycle, the whole speed regulation process can be realized. The details are as follows:

  MotorVelocityCurve(&curve);

   before the start of each speed regulation, it is necessary to set the removed start speed and target speed, so that the function will adjust the speed according to the set start speed and target speed.

4. Summary

   S-type velocity curve divides the whole motion process into seven stages, namely acceleration stage, uniform acceleration stage, deceleration stage, uniform speed stage, acceleration and deceleration stage, uniform deceleration stage and deceleration stage. The acceleration at the speed junction of different stages is continuous, and the change rate of acceleration is controllable, which overcomes the adverse effect of acceleration mutation in the trapezoidal velocity curve, This is a major advantage of the S-curve.

   however, compared with the T-shaped speed curve, the calculation amount of the S-shaped curve is much larger and the implementation is more complex than the T-shaped curve. However, these are no longer problems in the current processing system. Attention should be paid to the parameter setting, especially the tensile coefficient, which must be carefully adjusted according to the application. If it is too small, the intermediate speed regulation process will become flat, and the start and end stages will change relatively quickly; If it is too large, the and ending process will become relatively flat, but the middle part will change faster. It depends on the application requirements.

Welcome to: