Hash concept

A one-to-one mapping relationship can be established between the storage location of an element and its key through a function (hashFunc), so the element can be found quickly during search

The conversion function used in the hash method is called hash (hash) function, and the structure constructed is called hash table (or Hash list)

Mapping mode

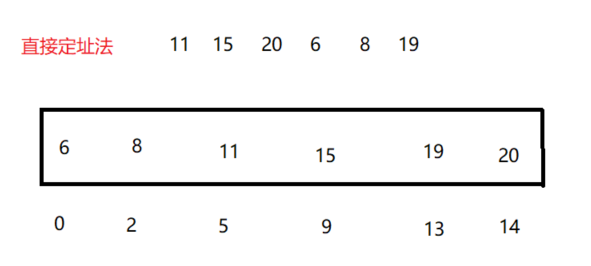
① Direct addressing method

The index relationship is established by the relative mapping or absolute position between the array and the data. At this time, the time complexity of adding, deleting, checking and modifying is O (1)
Defects:
1. If the data range is large, the direct customization method will waste a lot of space
2. Cannot process string, floating point number and other data, and cannot be used as the index of the array

Applicable to: integers and data sets

② Division residue method

Solve the problem of large data range

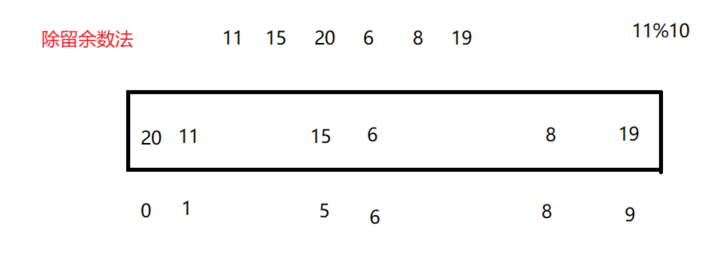
However, there is hash conflict in the divide and remainder method (different keywords calculate the same hash address through the same hash hash number, which is called hash conflict or hash collision)

Resolve hash conflicts

1. Closed hash (open addressing method)

① Linear detection

Linear detection can lead to a stampede effect (continuous position conflicts)

② Secondary detection

Secondary detection is more dispersed than linear detection data, which can effectively alleviate the stampede effect

Load factor (load factor) = number of valid data stored / space size
The larger the load factor, the higher the probability of conflict, the lower the efficiency of adding, deleting, searching and modifying, and the higher the space utilization
The smaller the load factor, the lower the probability of conflict, the higher the efficiency of adding, deleting, searching and modifying, and the lower the space utilization

Therefore, an important problem of hash table is to control the size of load factor

③ Node design

In order to determine whether a position in the array is empty, we use State to identify the State of the data in the array

	//Three states of data are listed
	enum State
	{
		EMPTY,//empty
		EXITS,//existence
		DELETE,//When deleting, you only need to change the status to DELETE, so as to realize "false" deletion
	};
    
	template<class K,class V>
	struct HashData
	{   
	    //Each data node is stored in the vector
	    //kv structure
		pair<K, V> _kv;
		
		State _state = EMPTY;
	};

④ Find operation

When the search is empty, it is not found. We control the size of the load factor to be less than 0.8, so there must be an empty location

		HashData<K,V>* Find(const K& key)
		{
			//Judge whether it is empty
			if (_table.size() == 0)
			{
				return nullptr;
			}
			HashFunc hf;
			size_t start = hf(key) % _table.size();
			size_t index = start;
			size_t i = 1;
			while (_table[index].state != EMPTY)
			{
				//eureka
				if (_table[index]._state==EXITS && _table[index]._kv.first == key)
				{
					return &_table[index];
				}
				//Look back
				//Linear detection secondary detection only needs to be changed to index=start+i*i;
				index =start+ i;
				index %= _table.size();
				++i;
			}
			return nullptr;
		}

⑤ Insert operation

The insertion operation needs to pay attention to the problem of capacity expansion. After capacity expansion, the data must be remapped

		bool Insert(const pair<K, V>& kv)
		{
			//Judge whether it exists
			HashData<K,V>* ret = Find(kv.first);
			if (ret)
			{
				return false;
			}
			//size==0
			if (_table.size() == 0)
			{
				_table.resize(10);
			}
			//Calculate load factor 
			else if ((double)_n/(double)_table.size()>0.8)
			{
				//After capacity expansion, all data must be remapped into the new array
				//Recreate the HashTable object and reuse its insert function
				HashTable<K, V,HashFunc> newHashTable;
				newHashTable.resize(2 * _table.size());
				//Traverse the data of the original Table
				for (auto& e : _table)
				{
					if (e._state == EXITS)
					{
						//Reuse Insert
						newHashTable.Insert(e._kv);
					}
				}
				_table.swap(newHashTable._table);
			}
			HashFunc hf;
			//If accessing data larger than size < capacity 
			size_t start = hf(kv.first) % _table.size();
			size_t index = start;
			size_t i = 1;
			//Linear detection or secondary detection
			while (_table[index]._state == EXITS)
			{
				index += start+i;
				index %= _table.size();
				++i;
			}
			_table[index]._kv = kv;
			_table[index]._state = EXITS;
			++_n;
		}

⑥ Delete operation

Once found, you only need to modify the status

	bool Erase(const K& key)
	{
		    //lookup
			HashData<K, V>* ret = Find(key);
			if (ret == nullptr)
			{
				return false;
			}
			else
			{
				//Modify node status
				ret->_state = DELETE;
				--_n;
				return true;
			}
	}

Complete code

#pragma once
#include<vector>
#include<iostream>
using namespace std;
//closeHash
namespace tzc
{
	enum State
	{
		EMPTY,
		EXITS,
		DELETE,
	};

	template<class K,class V>
	struct HashData
	{
		pair<K, V> _kv;
		State _state = EMPTY;
	};
	
	template<class K>
	struct HashFunc
	{
		int operator()(int i)
		{
			return i;
		}
	};
	template<>
	struct HashFunc<string>
	{
		size_t operator()(const string& s)
		{
			//return s[0];
			size_t value = 0;
			for (auto ch : s)
			{
				value += ch;
				value *= 131;
			}
			return value;
		}
	};
	struct pairHashFunc
	{
		size_t operator()(const pair<string, string>& kv)
		{
			size_t value = 0;
			//Take KEY as the standard
			for (auto& ch : kv.first)
			{
				value += ch;
				value *= 131;
			}
			return value;
		}
	};

	template<class K, class V,class HashFunc>
	class HashTable
	{
	public:

		bool Insert(const pair<K, V>& kv)
		{
			//Judge whether it exists
			HashData<K,V>* ret = Find(kv.first);
			if (ret)
			{
				return false;
			}
			//size==0
			if (_table.size() == 0)
			{
				_table.resize(10);
			}
			//Calculate load factor 
			else if ((double)_n/(double)_table.size()>0.8)
			{
				//After capacity expansion, all data must be remapped into the new array

				//Recreate the HashTable object and reuse its insert function
				HashTable<K, V,HashFunc> newHashTable;
				newHashTable.resize(2 * _table.size());
				for (auto& e : _table)
				{
					if (e._state == EXITS)
					{
						//Multiplex insertion
						newHashTable.Insert(e._kv);
					}
				}
				_table.swap(newHashTable._table);
			}
			HashFunc hf;
			size_t start = hf(kv.first) % _table.size();//table[]
			size_t index = start;
			size_t i = 1;
			//Linear detection or secondary detection
			while (_table[index]._state == EXITS)
			{
				index += start+i;
				index %= _table.size();
				++i;
			}
			_table[index]._kv = kv;
			_table[index]._state = EXITS;
			++_n;
		}
		HashData<K,V>* Find(const K& key)
		{
			//Judge whether it is empty
			if (_table.size() == 0)
			{
				return nullptr;
			}
			HashFunc hf;
			size_t start = hf(key) % _table.size();
			size_t index = start;
			size_t i = 1;
			while (_table[index].state != EMPTY)
			{
				//eureka
				if (_table[index]._state==EXITS && _table[index]._kv.first == key)
				{
					return &_table[index];
				}
				//Look back
				//Linear detection secondary detection only needs to be changed to index=start+i*i;
				index =start+ i;
				index %= _table.size();
				++i;
			}
			return nullptr;
		}
		bool Erase(const K& key)
		{
			HashData<K, V>* ret = Find(key);
			if (ret == nullptr)
			{
				return false;
			}
			else
			{
				ret->_state = DELETE;
				--_n;
				return true;
			}
		}
	private:
		vector<HashData<K,V>> _table;
		size_t _n;//The number of data stored in the array
	};
}

Problems with hash

For the following statements:

size_t start = hf(kv.first) % _table.size();

When the key stores string, user-defined type and other data, it cannot be converted into a mapping relationship and stored in the hash table

At this time, you need to implement the corresponding imitation function to convert the key module

 template<class K>
	struct HashFunc
	{
		int operator()(int i)
		{
			return i;
		}
	};
	
	//template specialization 
	template<>
	struct HashFunc<string>
	{
		size_t operator()(const string& s)
		{
			//return s[0];
			size_t value = 0;
			for (auto ch : s)
			{
				value += ch;
				value *= 131;
			}
			return value;
    }

It can be seen that if a type is used as a map/set key, it needs to be able to support size comparison

Do unordered_ map/unordered_ The key of set needs to be able to be converted into shaping (supporting modulo) and can be compared to equality

2. Hash

Hashing – hash bucket / zipper method
A single linked table pointer that stores a structure in an array

① Node design

Node stored in vector

template<class K,class V>
	struct HashNode
	{
		pair<K, V> _kv;
		HashNode<K, V>* _kv;
		HashNode(const pair<K, V>& kv)
			:_next(__nullptr)
			,_kv(kv)
		{
			
		}
	};

Private members contained in HashTable

		vector<Node*> _table;
		size_t _n = 0;//Number of valid data

② Insert operation

Capacity increase: it is agreed that when the load factor is equal to 1, it is necessary to increase capacity and reorganize, traverse the nodes in the old table and insert them into the new table
Hash table reorganization method 1: cleverly reuse the insert method

	bool Insert(const pair<K.V>& kv)
		{
			if (Find(kv.first))
			{
				return false;
			}
			if (_n == _table.size())
			{
				//Open up a new vector
				vector<Node*> newtable;
				size_t newSize = _table.size() == 0 ? 11: _table.size() * 2;
				newtable.resize(GetNextPrime(_table.size()), nullptr);

				//Traverse old tables
				for (size_t i = 0; i < _table.size(); ++i)
				{
					if (_table[i])
					{
						Node* cur = _table[i];
						while (cur)
						{
							Node* next = cur->_next;
							size_t index = cur->_kv.first % newtable.size();
							//Head insertion
							cur->_next = _table[index];
							_table[index] = cur;
							cur = next;
						}
						_table[i] = nullptr;
					}
				}
				//Old and new exchange
				_table.swap(newtable);
			}
			HashFunc fc;
			size_t index = fc(kv.first) % _table.size();
			Node* newnode = new Node(kv);
			//Head insert
			newnode->_next = _table[index];
			_table[index] = newnode;
			++_n;
			return true;
		}

Hash table reorganization method 2: the reorganization is realized by continuously inserting the head node of the old bucket node into the new corresponding vector

bool Insert(const pair<K.V>& kv)
	{
		if (Find(kv.first))
		{
			return false;
		}
		if (_n == _table.size())
		{
			vector<Node*> newtable(sizeof(_table.size()),(Node*)0);
			//Traverse old nodes
			for(size_t i=0;i<_table.size();i++)
			{
				Node* cur=_table[i];
				while(cur)
				{
					//Find out which bucket the node is in
					HashFunc fc;        
					size_t cur_bucket= fc(cur.first) % _table.size();
					//Four step delicate operation
					//1. Take the next node of cur to the head of the bucket
					_table[i]=cur->next;
					//2,3: insert the cur node into the new vector by head interpolation
					cur->next=newtable[cur_bucket];
					newtable[cur_bucket]=cur;
					//4.cur becomes the head of the old barrel again
					cur=_table[i];					
				}
			}
			_table.swap(newtable);
		}
		HashFunc fc;
		size_t index = fc(kv.first) % _table.size();
		Node* newnode = new Node(kv);
		//Head insert
		newnode->_next = _table[index];
		_table[index] = newnode;
		++_n;
		return true;
	}

③ Find operation

	Node* Find(const K& key)
		{
		
			if (_table.size() == 0)
			{
				return false;
			}
			HashFunc fc;
			size_t index = fc(key) % _table.size();
			Node* cur = _table[index];
			while(cur)
			{
				if (cur->_kv.first == key)
				{
					return cur;
				}
				else
				{
					cur = cur->_next;
				}
			}
			return nullptr;
		}

④ Delete operation

		bool Erase(const K& key)
		{
			HashFunc fc;
			size_t index = fc(key) % _table.size();
			Node* prev = nullptr;
			Node* cur = _table[index];
			while (cur)
			{
				if (cur->_kv.first == key)
				{   
					//The header node is deleted
					if (_table[index] == cur)
					{
						_table[index] = cur->_next;
					}
					else
					{
						prev->_next = cur->_next;
					}
					--_n;
					delete cur;
					return true;
				}
				prev = cur;
				cur = cur->_next;
			}
		}

Advantages of hash bucket:
1. High space utilization
2. Extreme situations (all conflicts) and Solutions

Resolution of hash bucket conflict

If the data is concentrated on several buckets at this time, the time complexity will be very large when searching and deleting, which may be equal to O (N)

1. Therefore, the load factor can be controlled
The load factor of open hash may be greater than 1, so the control load factor is generally [0,1]

2. Secondly, when there are few data, the load factor is very low, but most of the data conflict
The bucket with more data can be used to change its data structure into a red black tree

Design of bucket size:
Try to make the size of the table prime, so it is less likely to conflict

const int PRIMECOUNT = 28;

const size_t primeList[PRIMECOUNT] ={ 
 53ul, 97ul, 193ul, 389ul, 769ul, 1543ul, 3079ul, 6151ul, 12289ul,
 24593ul, 49157ul, 98317ul, 196613ul, 393241ul, 786433ul, 1572869ul, 3145739ul, 
 6291469ul,12582917ul, 25165843ul, 50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul, 1610612741ul, 3221225473ul, 4294967291ul};
 
   size_t GetNextPrime(size_t prime)
	{
	 size_t i = 0; 
	 for(; i < PRIMECOUNT; ++i) 
	 { 
		 if(primeList[i] > primeList[i]) 
		 return primeList[i]; 
	 } 
   return primeList[i];
   }

encapsulation

① Iterator

In addition to passing the current node pointer, the iterator should also pass in the hash table
Because + + cannot find the position of the next bucket when the iterator reaches the end node of a bucket
At this time, the hash table is passed in and the position of the next bucket is recalculated

	// forward declaration  					// Default parameters are only given when defining
	template<class K, class T, class KeyOfT, class HashFunc>
	class HashTable;

	// iterator 
	template<class K, class T, class KeyOfT, class HashFunc = Hash<K>>
	struct __HTIterator
	{
		typedef HashNode<T> Node;
		typedef __HTIterator<K, T, KeyOfT, HashFunc> Self;
		
		typedef HashTable<K, T, KeyOfT, HashFunc> HT;
		Node* _node;
		HT* _pht;
			//Hash table passed to iterator
		__HTIterator(Node* node, HT* pht)
			:_node(node)
			, _pht(pht)
		{}

		Self& operator++()
		{
			// 1. Traverse the nodes of each bucket one by one
			if (_node->_next)
			{
				_node = _node->_next;
			}
			//To the next bucket
			else
			{
				//size_t index = HashFunc()(KeyOfT()(_node->_data)) % _pht->_table.size();
				KeyOfT kot;
				HashFunc hf;
				size_t index = hf(kot(_node->_data)) % _pht->_table.size();

				++index;
				while (index < _pht->_table.size())
				{
					if (_pht->_table[index])
					{
						//_ You need Shen Mingyuan for pht to access private members
						_node = _pht->_table[index];
						
						return *this;
					}
					//Empty bucket
					else
					{
						++index;
					}
				}

				_node = nullptr;
			}

			return *this;
		}
		//The underlying implementation uses a one-way linked list without overloading--
		T& operator*()
		{
			return _node->_data;
		}

		T* operator->()
		{
			return &_node->_data;
		}

		bool operator != (const Self& s) const
		{
			return _node != s._node;
		}

		bool operator == (const Self& s) const
		{
			return _node == s.node;
		}
	};

②hash functions

hash fuctions is an imitation function to solve the problem of modulo of stored values
① char,int, long, etc. are integer types and return values directly
② Strings and built-in types can only be returned after special operations

And the returned value should consider the hash conflict

//Convert Key to realize modular operation
	template<class K>
	struct Hash
	{
		size_t operator()(const K& key)
		{
			return key;
		}
	};
	// Specialization string
	template<>
	struct Hash < string >
	{
		size_t operator()(const string& s)
		{
			// BKDR Hash
			size_t value = 0;
			for (auto ch : s)
			{
				value += ch;
				value *= 131;
			}
			return value;
		}
	};

③ Hash table

	
	//Node storage T
	template<class T>
	struct HashNode
	{
		HashNode<T>* _next;
		T _data;

		HashNode(const T& data)
			:_next(nullptr)
			, _data(data)
		{}
	};
  template<class K, class T, class KeyOfT, class HashFunc = Hash<K>>
	class HashTable
	{
		typedef HashNode<T> Node;

		template<class K, class T, class KeyOfT, class HashFunc>
		friend struct __HTIterator;//Class template parameter friend
	public:
		typedef __HTIterator<K, T, KeyOfT, HashFunc> iterator;

		HashTable() = default; // Displays the default construction for the specified build
	   //Deep copy
		HashTable(const HashTable& ht)
		{
			_n = ht._n;
			_table.resize(ht._table.size());
			for (size_t i = 0; i < ht._table.size(); i++)
			{
				Node* cur = ht._table[i];
				while (cur)
				{
					Node* copy = new Node(cur->_data);
					// Traversal insertion
					copy->_next = _table[i];
					_table[i] = copy;

					cur = cur->_next;
				}
			}
		}
		
		HashTable& operator=(HashTable ht)
		{
			_table.swap(ht._table);
			swap(_n, ht._n);

			return *this;
		}

		~HashTable()
		{
			for (size_t i = 0; i < _table.size(); ++i)
			{
				Node* cur = _table[i];
				while (cur)
				{
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_table[i] = nullptr;
			}
		}
		//Calculate the number of barrels in the table
		size_t bucket_count()const
		{
			return  _table.size();
		}
		
		iterator begin()
		{
			size_t i = 0;
			while (i < _table.size())
			{
				if (_table[i])
				{
					return iterator(_table[i], this);
				}

				++i;
			}

			return end();
		}

		iterator end()
		{
			return iterator(nullptr, this);
		}

		size_t GetNextPrime(size_t prime)
		{
			const int PRIMECOUNT = 28;
			static const size_t primeList[PRIMECOUNT] =
			{
				53ul, 97ul, 193ul, 389ul, 769ul,
				1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
				49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
				1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,
				50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,
				1610612741ul, 3221225473ul, 4294967291ul
			};
			size_t i = 0;
			for (; i < PRIMECOUNT; ++i)
			{
				if (primeList[i] > prime)
					return primeList[i];
			}

			return primeList[i];
		}
		//Calculate the maximum number of barrels
		size_t maxbucket_count()const
		{
			return primeList[PRIMECOUNT-1];
		}
		
		//Hash bucket implementation
		pair<iterator, bool> Insert(const T& data)
		{
			KeyOfT kot;
			// eureka
			auto ret = Find(kot(data));
			if (ret != end())
				return make_pair(ret, false);

			HashFunc hf;
			// When the load factor reaches 1, increase the capacity
			if (_n == _table.size())
			{
				vector<Node*> newtable;
				//size_t newSize = _table.size() == 0 ? 8 : _table.size() * 2;
				//newtable.resize(newSize, nullptr);
				newtable.resize(GetNextPrime(_table.size()));

				// Traverse the nodes in the old table and map them to the new table
				for (size_t i = 0; i < _table.size(); ++i)
				{
					if (_table[i])
					{
						Node* cur = _table[i];
						while (cur)
						{
							Node* next = cur->_next;
							size_t index = hf(kot(cur->_data)) % newtable.size();
							// Head insert
							cur->_next = newtable[index];
							newtable[index] = cur;

							cur = next;
						}
						_table[i] = nullptr;
					}
				}

				_table.swap(newtable);
			}

			size_t index = hf(kot(data)) % _table.size();
			Node* newnode = new Node(data);

			// Head insert
			newnode->_next = _table[index];
			_table[index] = newnode;
			++_n;

			return make_pair(iterator(newnode, this), true);
		}

		iterator Find(const K& key)
		{
			if (_table.size() == 0)
			{
				return end();
			}

			KeyOfT kot;//Get key
			HashFunc hf;//Transform key module
			size_t index = hf(key) % _table.size();
			Node* cur = _table[index];
			while (cur)
			{
				if (kot(cur->_data) == key)
				{
					return iterator(cur, this);
				}
				else
				{
					cur = cur->_next;
				}
			}

			return end();
		}

		bool Erase(const K& key)
		{
			size_t index = hf(key) % _table.size();
			Node* prev = nullptr;
			Node* cur = _table[index];
			while (cur)
			{
				if (kot(cur->_data) == key)
				{
					if (_table[index] == cur)
					{
						_table[index] = cur->_next;
					}
					else
					{
						prev->_next = cur->_next;
					}

					--_n;
					delete cur;
					return true;
				}

				prev = cur;
				cur = cur->_next;
			}

			return false;
		}

	private:
		vector<Node*> _table;
		size_t _n = 0;         // Number of valid data
	};

UnorderedSet

Using set is convenient to find elements quickly
The set with red black tree at the bottom has the function of automatic sorting (medium order traversal), while the unordered set with hash table at the bottom does not

namespace tzc
{
	template<class K>
	class unordered_set
	{
		//Get key
		struct SetKeyOfT
		{
			const K& operator()(const K& k)
			{
				return k;
			}
		};
	public:
		typedef typename OpenHash::HashTable<K, K, SetKeyOfT >::iterator iterator;
		iterator begin()
		{
			return _ht.begin();
		}

		iterator end()
		{
			return _ht.end();
		}

		pair<iterator, bool> insert(const K k)
		{
			return _ht.Insert(k);
		}

	private:
		OpenHash::HashTable<K, K, SetKeyOfT> _ht;//Hash table implemented by open hash
	};
}

UnorderedMap

namespace tzc
{
	template<class K, class V>
	class unordered_map
	{
		//Get Key
		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
		typedef typename OpenHash::HashTable<K, pair<K, V>, MapKeyOfT>::iterator iterator;
		iterator begin()
		{
			return _ht.begin();
		}

		iterator end()
		{
			return _ht.end();
		}

		pair<iterator, bool> insert(const pair<K, V>& kv)
		{
			return _ht.Insert(kv);
		}

		V& operator[](const K& key)//Overload []
		{
			pair<iterator, bool> ret = _ht.Insert(make_pair(key, V()));
			return ret.first->second;
		}

	private:
		OpenHash::HashTable<K, pair<K, V>, MapKeyOfT> _ht;
	};
}