⭐ ♪ previous words ⭐ ️
hello everyone! This article will introduce the sword finger offerOJ question, which comes from Li Kou[ Sword finger Offer 55 - II balanced binary tree ]This paper will introduce the balanced binary tree based on the concept of binary tree and the depth of binary tree, and show that the code language is Java and C/C + +.
📒 Blog home page: Blog home page without flower smell
🎉 Welcome to pay attention 🔎 give the thumbs-up 👍 Collection ⭐ Leave a message 📝
📌 This article is original by Huawen, CSDN first!
📆 Starting time: 🌴 December 23, 2021 🌴
✉️ Persistence and hard work will surely bring poetry and distance!
💭 Recommended books: 📚 Sword finger offer special edition, 📚 Sword finger offer 2nd Edition
💬 Refer to the online programming website: 🌐 Niuke network🌐Force buckle
The blogger's code cloud gitee, usually the program code written by the blogger is in it.
The github of the blogger is usually the program code written by the blogger.
🙏 The author's level is very limited. If you find an error, you must inform the author in time! Thank you, thank you!

⭐ Offer 55 - II balanced binary tree ⭐ ️
🔐 Title details
Enter the root node of a binary tree to judge whether the tree is a balanced binary tree. If the depth difference between the left and right subtrees of any node in a binary tree is no more than 1, it is a balanced binary tree.
Example:
Given binary tree [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
Returns true.
Given binary tree [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/ \
4 4
Returns false.
| Source: LeetCode link: Sword finger Offer 55 - II balanced binary tree |
|---|
💡 Problem solving ideas
Preliminary knowledge:
Data structure tree, tree depth and binary tree depth calculation method, binary tree, balanced binary tree, the first three points have been in the blog Sword finger Offer 55 - I. depth of binary tree Yes, I will not repeat it here.
Question: what is a balanced binary tree?
If any node of a binary tree satisfies that the depth difference between its left and right subtrees is no more than 1, the binary tree is a balanced binary tree.
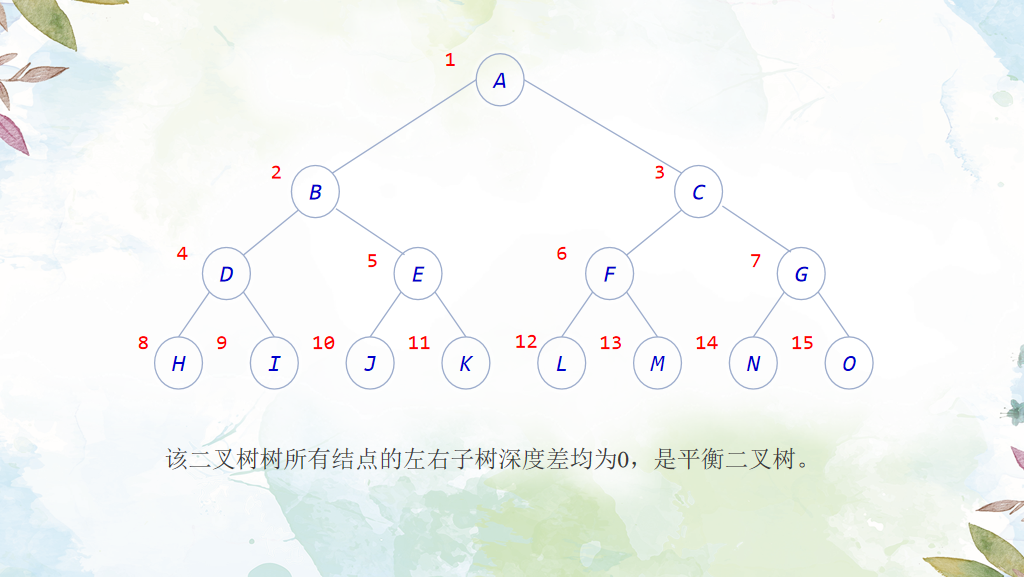
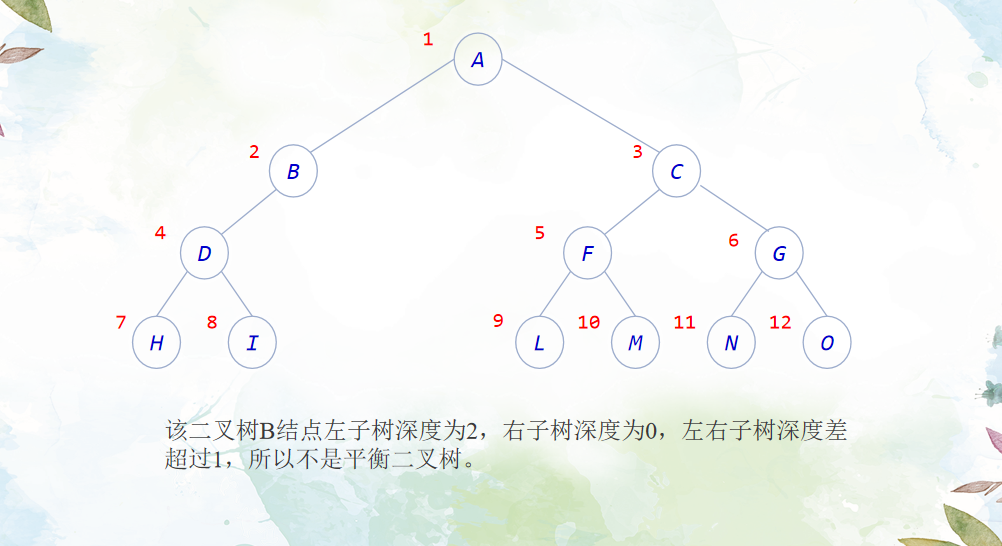
Problem solving ideas:
Starting from the root node, judge whether the depth difference between the left and right subtrees of all nodes is less than 1. If this condition is met, return true. Otherwise, return false. If the node is null, return true.
From a single subtree node in a binary tree, the depth difference between the left and right subtrees of this node is not greater than 1, and the root nodes of the left and right subtrees of this node also meet that the depth difference between the subtrees is not greater than 1. In this way, it can be determined that the binary tree is a balanced binary tree.
🔑 source code
Java:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxDeep(TreeNode subtree) {
if (subtree == null) {
return 0;
}
return 1 + Math.max(maxDeep(subtree.left), maxDeep(subtree.right));//Find depth
}
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
}
int ret = Math.abs(maxDeep(root.left) - maxDeep(root.right));
if (ret <= 1 && isBalanced(root.left) && isBalanced(root.right)) {
return true;//Judge balanced binary tree
}
return false;
}
}
C:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int max(int a, int b)
{
return a > b ? a : b;
}
int maxDeep(struct TreeNode* subtree)
{
if (subtree == NULL)
{
return 0;
}
return 1 + max(maxDeep(subtree->left), maxDeep(subtree->right));
}
bool isBalanced(struct TreeNode* root){
if (root == NULL)
{
return true;
}
int ret = fabs(maxDeep(root->left) - maxDeep(root->right));
if (ret <= 1 && isBalanced(root->left) && isBalanced(root->right))
{
return true;
}
return false;
}
C++:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int maxDeep(TreeNode * subtree) {
if (subtree == NULL) {
return 0;
}
return 1 + max(maxDeep(subtree->left), maxDeep(subtree->right));
}
bool isBalanced(TreeNode* root) {
if (root == NULL) {
return true;
}
int ret = abs(maxDeep(root->left) - maxDeep(root->right));
if (ret <= 1 && isBalanced(root->left) && isBalanced(root->right)) {
return true;
}
return false;
}
};
🌱 summary
Starting from the root node, judge whether the depth difference between the left and right subtrees of all nodes is less than 1. If this condition is met, return true. Otherwise, return false. If the node is null, return true.
Similar questions are as follows:
110. Balanced binary tree
