I believe that many peers will want to change jobs for many reasons, whether they are unhappy or want to change jobs and increase their salary. In such an internal industry, we are faced with the situation of "interviewing to build rockets and screwing screws at work". In view of the current situation, the blogger has worked hard to sort out the skills of building rockets full of dry goods, and this blogger spent two months, Sort out and summarize the common interview questions of java whole ecological knowledge system! The total number of words is up to one million! It's full of dry goods, updated every day, pay attention to me, don't get lost, use powerful induction and summary, new and detailed explanation to keep the attention of ape friends, and hope to help ape friends cope with the written interview! Of course, if there are any mistakes in summary, please point out and correct them! If there is infringement, please contact blogger QQ1062141499!
catalogue
1 what is recursion? What are the advantages and disadvantages of recursion?
2 what is complexity? Why complexity analysis?
3 what is time complexity? What is spatial complexity?
4 how to perform complexity analysis?
5. Differences between O (1), O (n), O (N2), O (logn), O (nlogn)
6 what are the common encryption algorithms? Is it symmetrical?
7 difference between array and linked list
8 with the same complexity, why is insert sort more popular than bubble sort?
1 what is recursion? What are the advantages and disadvantages of recursion?
Recursion: the process of directly or indirectly calling its own algorithm
Conditions for using recursion are met:
- The subproblem is similar and simpler
- There must be an exit
advantage:
- Concise code
- In line with thinking habits, easy to understand
Disadvantages:
- Low efficiency
- The recursion level is too deep, consuming memory and prone to stack overflow. If it must be used, it is best to use cache to avoid the same calculation and limit the number of recursive calls
2 what is complexity? Why complexity analysis?
Complexity
- Complexity is also called progressive complexity, including time complexity and space complexity. It is used to analyze the growth relationship between algorithm execution efficiency and data scale. It can be roughly expressed that the higher the complexity of the algorithm, the lower the execution efficiency.
- Complexity describes the growth of algorithm execution time or memory space with the size of data.
Why complexity analysis?
- With the help of complexity analysis, it is helpful to write better code and reduce cost.
- Complexity analysis does not depend on execution environment, low cost, high efficiency, easy operation and strong guidance. It is a set of theoretical methods.
3 what is time complexity? What is spatial complexity?
- The full name of time complexity is asymptotic time complexity, which represents the growth relationship between the execution time of the algorithm and the data scale.
- The full name of spatial complexity is asymptotic space complexity, which represents the growth relationship between the storage space of the algorithm and the data scale.
4 how to perform complexity analysis?
Time complexity analysis:
1. Representation of large o complexity: T(n) = O(f(n)), O in the formula represents the execution time of the code, and T(n) is directly proportional to the expression of f(n)
- Focus only on the code that executes the loop the most times
- The total complexity is equal to the complexity of the code with the largest order of magnitude
- The complexity of nested code is equal to the product of the complexity of inner and outer nested code
2. Best case time complexity: the time complexity of code execution in the best case
3. Worst case time complexity: the time complexity of code execution in the worst case
4. Average time complexity: the weighted average of the number of times code is executed in all cases
5. Sharing time complexity: when there are very few high-level complexities and there is a time series relationship, these high-level complexities can be shared equally to the low-level complexity. Generally, the sharing result is equal to the low-level complexity
Spatial complexity analysis:
- Similar to time complexity analysis, it focuses on the growth relationship between the storage space of the algorithm and the data scale
Common complexity:
- The common complexity is not much, from low to high order: O(1), O(logn), O(n), O(nlogn), O(n2)
5. Differences between O (1), O (n), O (N2), O (logn), O (nlogn)
When describing algorithm complexity, O (1), O (n), O (logn) and O (nlogn) are often used to represent the corresponding complexity. However, at present, these methods are also used to represent spatial complexity by default.
Then, O(1), O(n), O(logn), O(nlogn) can be regarded as representing both algorithm complexity and spatial complexity.
In the form of large o plus (), it actually wraps a function f(),O (f()), indicating the relationship between the time / space consumption of an algorithm and the amount of data growth. Where n represents the amount of input data.
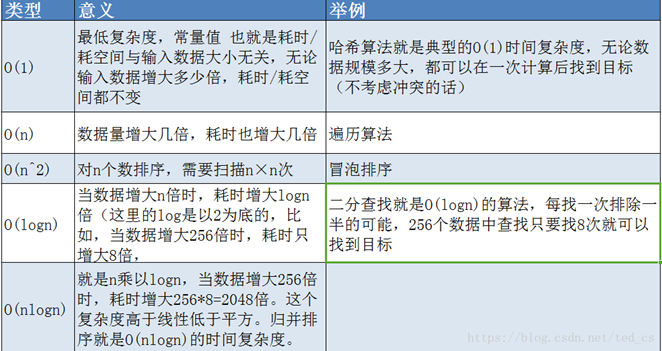
If ax=N (a > 0 and a ≠ 1), then the number x is called the logarithm of n with a as the base, recorded as x=logaN, and read as the logarithm of n with a as the base, where a is called the base of logarithm and N is called true.
6 what are the common encryption algorithms? Is it symmetrical?
- Common symmetric encryption algorithms: DES, AES, 3DES, RC2, RC4
- Common asymmetric encryption algorithms: RSA, DSA, ECC
- Encryption algorithm of one-way hash function: MD5, SHA
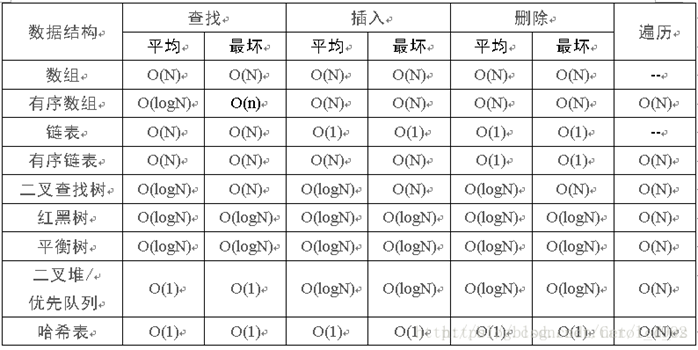
7 difference between array and linked list
- Access mode: the array can be accessed sequentially or randomly; Linked lists can only be accessed sequentially
- Storage location: logically adjacent elements of the array are also adjacent in the physical storage location; The physical storage location of the linked list is uncertain and generally scattered
- Storage space: because the linked list has a pointer field, the storage density is not as large as the array
- Search by sequence number: the array can be accessed randomly, and the time complexity is O(1); The linked list does not support random access and requires O(n) on average;
- Search by value: if the array is out of order, the time complexity of the array and the linked list is O(n). When the array is in order, binary search can be used to reduce the time complexity to O(log n)
- Insert and delete: the array needs to move n/2 elements on average; The linked list only needs to modify the pointer
- Space allocation: array. In the case of static storage allocation, the number of storage elements is limited. In the case of dynamic storage allocation, although the storage space can be expanded, a large number of elements need to be moved, which reduces the operation efficiency, and if there is no larger continuous storage space in the memory, the allocation will fail; Linked list, the stored node space can only be allocated when needed. As long as there is space in the memory, it can be allocated. The operation is flexible and efficient
8 with the same complexity, why is insert sort more popular than bubble sort?
We learned about bubble sorting and insert sorting. The time complexity and space complexity are the same:
- Best case time complexity: O(n)
- Worst case time complexity: O(n2)
- Average time complexity: O(n2)
- Space complexity: O(1), stable sorting algorithm
But why do you use too much insertion sorting in actual development?
The reasons are as follows:
- For the same array, bubble sort and insert sort, the number of interactive data is the same in the optimal case (that is, the reverse order of the original array is the same)
- For each data exchange, bubble sorting of mobile data is more complex than insert sorting. Bubble sort is assigned 3 times and insert sort is assigned 1 time
Code comparison:
//Bubble sorting
int temp = array[j + 1];
array[j+1] = array[j];
array[j] = temp;
hasSwitch = true;//There is data exchange
//Insert sort
if (array[j] > value) {
array[j+1] = array[j];
} else {
break;
}
Test code:
package Lee.interview.algorithm;
import java.util.Random;
/**
* Test bubble sort
* @author Lee
* @date 2020-04-10 09:36:54
*/
public class CompareBubbleAndInsertionSort {
public static void main(String[] args) {
//Generate two random arrays of the same length
int length = 10000;
int[] array_1 = generateArray(length);
int[] array_2 = new int[length];
System.arraycopy(array_1, 0, array_2, 0, length);
print(array_1);
print(array_2);
//Compare the time consumption of bubble sort and insert sort
long array_1_start = System.currentTimeMillis();
bubbleSort(array_1);
System.out.println("bubbleSort cost time : " + (System.currentTimeMillis() - array_1_start));
long array_2_start = System.currentTimeMillis();
insertionSort(array_2);
System.out.println("insertionSort cost time : " + (System.currentTimeMillis() - array_2_start));
//Print the sorted two arrays to see if the results are correct
print(array_1);
print(array_2);
}
/**
* Generate random array
* @param length
* @return
*/
private static int[] generateArray(int length) {
Random r = new Random();
int[] array = new int[length];
for (int i = 0; i <array.length; i++) {
array[i] = r.nextInt(length);
}
return array;
}
/**
* Bubble sorting
* @param array
*/
private static void bubbleSort(int[] array) {
for (int i = 0; i <array.length; i++) {
//Flag for early exit from bubbling cycle
boolean hasSwitch = false;
//Because the subscripts of J and j+1 are used for comparison, the maximum value of J is the array length - 2
for (int j = 0; j <array.length - (i+1); j++) {
if (array[j] > array[j + 1]) {
int temp = array[j + 1];
array[j+1] = array[j];
array[j] = temp;
hasSwitch = true;//There is data exchange
}
}
//No data exchange exits the loop
if (!hasSwitch) {
break;
}
}
}
/**
* Insert sort
*/
private static void insertionSort(int[] array) {
for (int i = 1; i <array.length; i++) {
int j = i - 1;
int value = array[i];
for (; j >= 0; j--) {
if (array[j] > value) {
array[j+1] = array[j];
} else {
break;
}
}
array[j+1] = value;
}
}
/**
* Print array
* @param array
*/
private static void print(int[] array) {
for(int i : array) {
System.out.print(i);
}
System.out.println();
}
}
Print results:
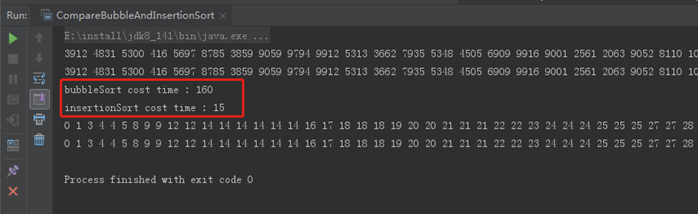
With the increase of array length, bubble sort takes more time than insert sort.