Key words in this article: methods, nesting, recursion, classical problems

1. Nesting of methods

1. Conceptual Interpretation

The concept of method nesting is actually better understood, that is, when a method is called, it encounters another method call. At the beginning of contact, although you can logically understand why the result is like this, you still feel a bit detached from the process of code execution.

2. Method Nesting

In programming, the most common is the nesting of calls between methods, because typically, we don't solve a problem by just one method.And if a method provides a very powerful function, it is bound that the code logic and parameter list will become relatively complex, which is not conducive to modification and use, so we hope that each method is a small edge to solve specific problems, and complete a more complex function by using a combination of methods, just like Rayn's seven-star knife..

For example, we already have two methods: one for calculating the area of a circle and the other for calculating the area of a rectangle. If we need to calculate the surface area of a cylinder now, do we need to rewrite the whole method?Of course not, because the surface area of a cylinder can be calculated just by the area of the base of two cylinders (circle) plus the area of the side of the cylinder (rectangle), we only need reasonable incoming parameters and return of the values.

public class Test{
    public static void main(String[] args){
        // Calculate the area of a cylinder, known base radius and height
        int radius = 5;
        int height = 10;
        // Call Calculate Cylinder Surface Area
        double area = getColumnArea(radius,height);
        // Output Results
        System.out.println("The surface area of the cylinder is:" + area);
    }
    public static double getCircleArea(double radius){
        // Return after calculating the area based on the radius of the circle
        return Math.PI * Math.pow(radius,2);
    }
    public static double getRectangleArea(double width,double height){
        // Return after calculating area based on width and height
        return width * height;
    }
    public static double getColumnArea(double radius,double height){
        // Calculate the bottom area - > just the width of the side area
        double baseArea = getCircleArea(radius);
        // Calculate Side Area
        double lateralArea = getRectangleArea(baseArea,height);
        // Return from base and side area calculations
        return baseArea * 2 + lateralArea;
    }
}

So what is the process of executing the whole method?It's still a sequential structure, and when a called method is fully executed, the next steps will continue. We can describe this process as follows: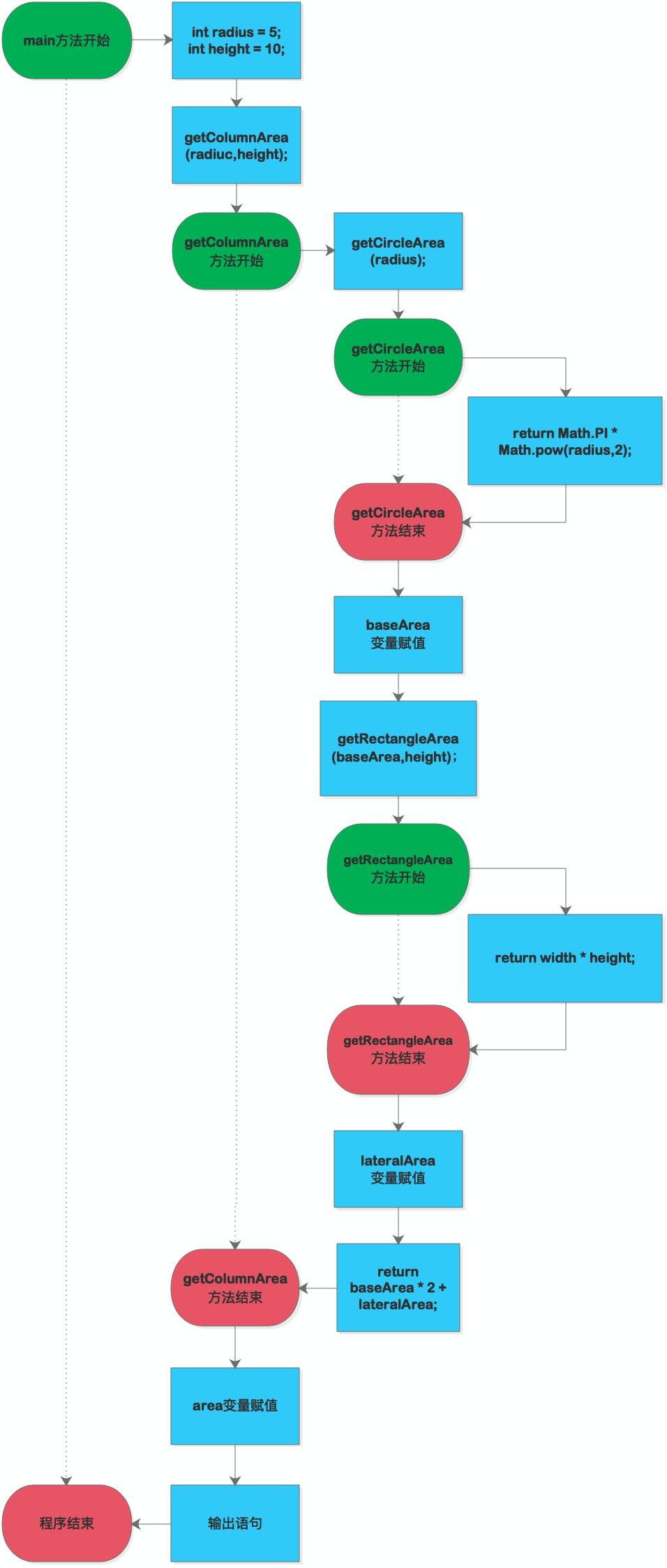

3. Construct Nesting

In previous articles, you have been introduced to the overload of the constructor, which can be used to initialize different numbers of attributes by directly clicking on the portal: Java Initialization Object Tool-Constructor .However, there is a problem when using the constructor. The main purpose of the constructor is to assign values to attributes, but when the constructor is overloaded, it will find that there is the same redundancy of code and that many of the same assignment statements will appear. As a severe OCD patient, this is intolerable. See the following example:

public class Person{
    // One parameter constructor
    public Person(String name){
        this.name = name;
    }
    // A two-parameter constructor that assigns values to the name and age attributes
    public Person(String name,int age){
        this.name = name;
        this.age = age;
    }
    // A three-parameter constructor that assigns values to name, age, and job attributes
    public Person(String name,int age,String job){
        this.name = name;
        this.age = age;
        this.job = job;
    }
    public String name;
    public int age;
    public String job;
}

In the example above, three constructors are defined to meet different initialization needs (and we can define more of them, of course), but you can see that many assignment statements are duplicated, and you can reduce the amount of code by invoking constructors with each other.Constructors make calls to each other in the current class, using this(), fill in the appropriate parameters in parentheses, and modify the code as follows.

public class Person{
    // One parameter constructor
    public Person(String name){
        this.name = name;
    }
    // A two-parameter constructor that assigns values to the name and age attributes
    public Person(String name,int age){
        this(name);
        this.age = age;
    }
    // A three-parameter constructor that assigns values to name, age, and job attributes
    public Person(String name,int age,String job){
        this(name,age);
        this.job = job;
    }
    public String name;
    public int age;
    public String job;
}

If you use a three-parameter constructor in the test class to initialize a Person object: Person person = new Person("small sheet", 25, "engineer"); the following procedure is performed: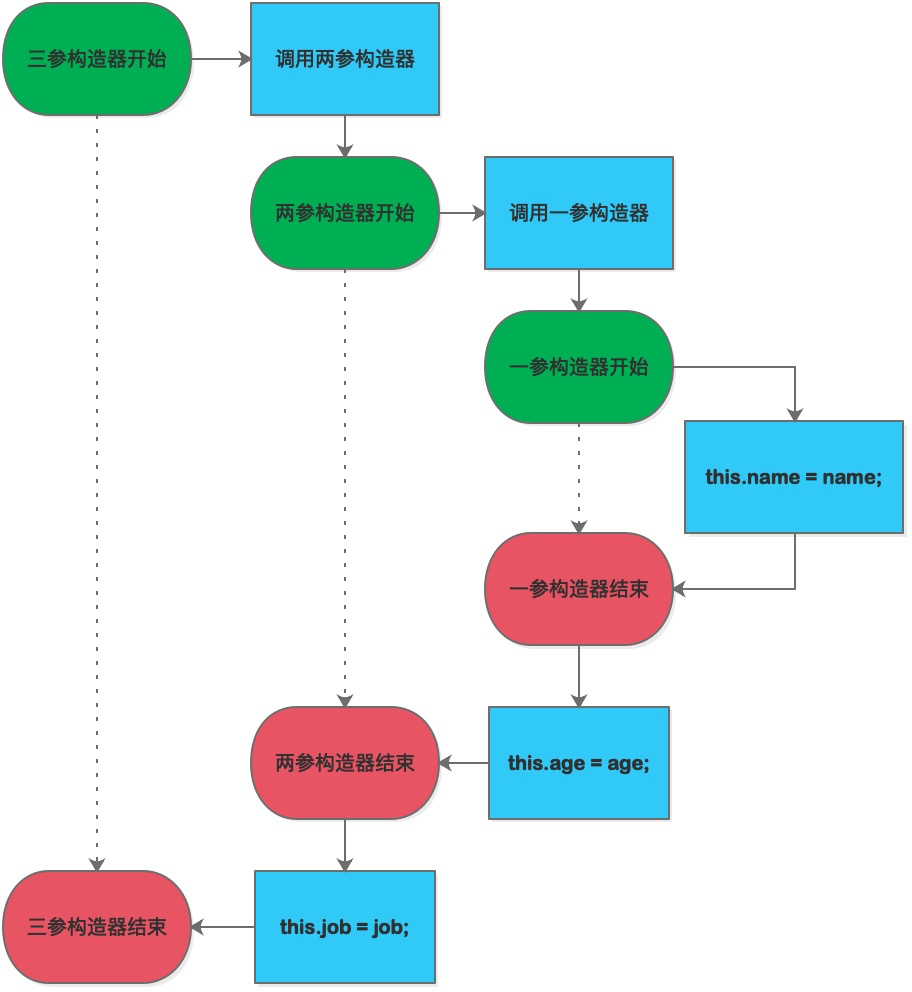

2. Recursion of methods

1. Conceptual Interpretation

Recursion is a computational process or method, a method to solve problems by breaking them down into similar subproblems. So what are the same subproblems?It's about splitting up a big problem and getting the same rule, or the same operation, such as the simplest factorial calculation.If we need to calculate the factorial of 4, write it out mathematically directly as 4! = 4 x 3 x 2 x 1.
So how do we solve this problem with computers?Of course, we can use loops, multiplying a given number up to:

public class Test{
    public static void main(String[] args){
        int n = 4;
        int result = 1;
        for(int i = n;i <= 1;i--){
            result *= i;
        }
        System.out.println(result);
    }
}

But actually this can be summarized or broken down into a rule: n! = n x (n - 1)!, n < 2; n! = 1, n = 1.So what's the difference between this and circularity?The difference is that when we use loops, we translate this computing process into code that the computer can read and execute directly without meaning and, in some cases, not all problems can be solved through a looping structure.On the other hand, computational theory can prove that recursion can completely replace loops, but for performance reasons, we do not intentionally replace loops with recursion and prefer to use recursion to solve a particular kind of problem.

2. Recursive thinking

As you can see from the introduction above, we want to use recursive thinking to get as close as possible to the description of the original problem and to solve it well.From a code perspective, recursive methods are summarized in one sentence: <font color="red">Call yourself </font>.Why do you say that?Because the entire execution process is achieved by repeating one step, the result of each step comes from the previous step or step.Then the question comes. When did it come to an end?This leads to the concept of a recursive export.
Just as a loop needs a termination condition, recursion calls itself constantly to get the results it needs, so it also needs a termination condition, which is usually set more clearly: when a definite result can be obtained, there is no need to make recursive calls anymore, and then the specific result can be returned directly, for example, if we use recursionReturn to realize factorial:

public class Test{
    public static void main(String[] args){
        int n = 4;
        int result = getFactorial(n);
        System.out.println(result);
    }
    // Define a method for calculating the factorial of n, regardless of N < 0
    public static int getFactorial(int n){
        // Recursive export
        // Describes that when n = 1, the result of the factorial is 1, returning the determined result directly
        if(n == 1){
            return 1;
        }else{
            // By law, the factorial of n-1 should be obtained first
            // Describes when n is greater than or equal to 2, n! = n x (n - 1)!
            return n * getFactorial(n - 1);
        }
    }
}

When we have compiled a formula or described a rule, we can try to think in the following ways:

• The first step is to determine the recursive export, which is the criterion, usually the exit, which is the value of the incoming parameter when a deterministic value can be obtained.
• The next step is to determine the content of the export, that is, the determinant value obtained when the criteria for judgment are met.
• Finally, the part called recursively is expressed in an expression according to the law summarized.

3. Execution process

If you understand the process of decomposition, then we have implemented this description from code, and when n = 1, you can get the definite result directly: 1; when n = 2, you pass in n - 1 as a parameter by recursive call (call yourself), which means you want to get the recursive value of n - 1, and N -1 After passing in, if you cannot get a definite result, you will continue to call, then the overall operation can be represented by the following figure: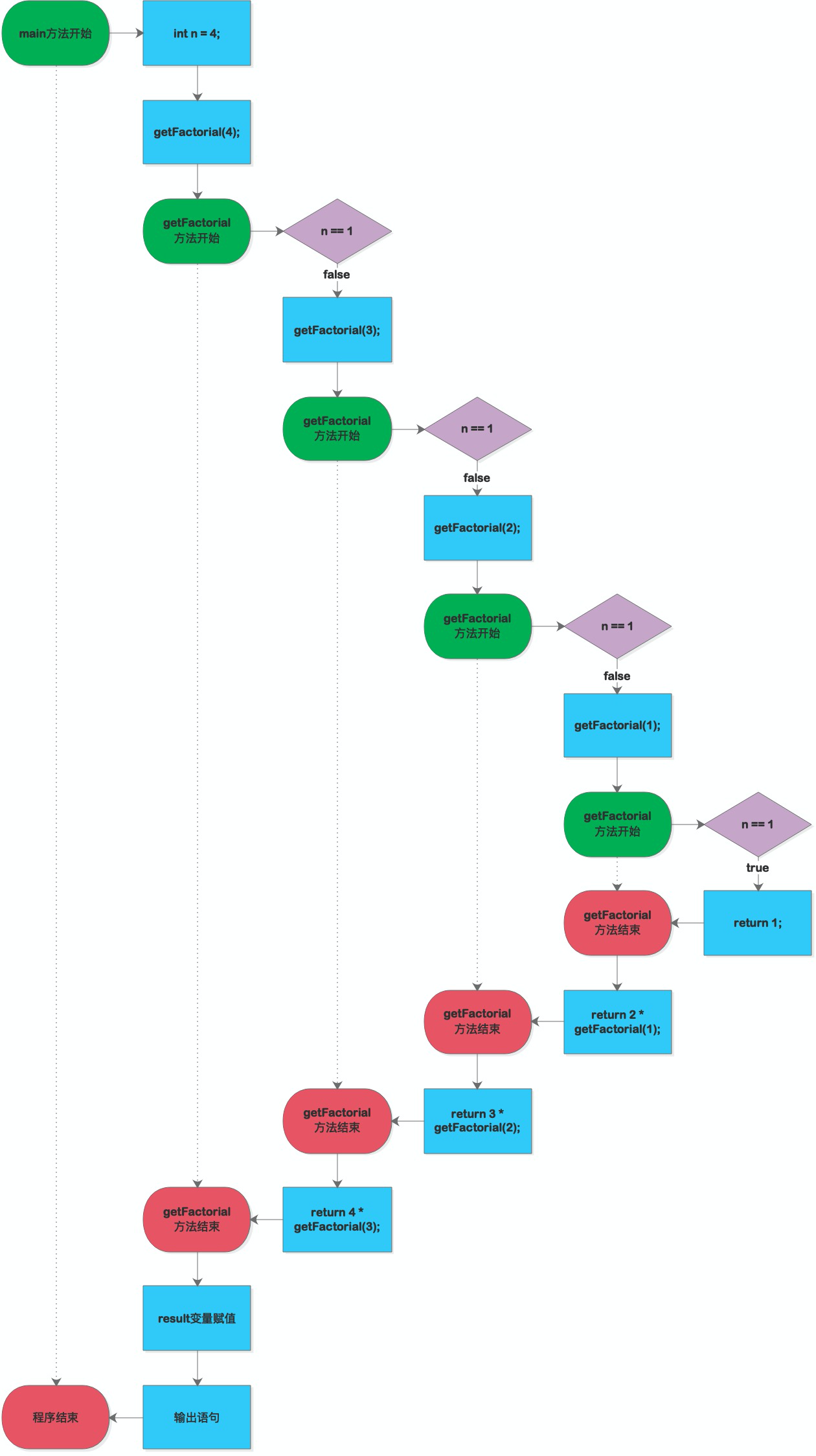

4. Classic Questions

• Fibonacci series

The Fibonacci sequence is a very classical one, the first one is 1, the second one is 1. Starting with the third one, the values of each item are the sum of the first two items. To sort out mathematically, f(n) = 1 when n = 1 or n = 2 and f(n) = f(n - 1) + f(n - 2) when n = 3.Following the previous steps, we can make sure that the exit is n = 1 or n = 2, and the result is: 1, the part called recursively is: f(n - 1) + f(n - 2), from which we write the program:

public class Test{
    public static void main(String[] args){
        int n = 5;// Customize a positive integer n
        int result = f(n);
        System.out.println(result);
    }
    public static int f(int n){
        // Recursive exit: terminate the call when n = 1 or n = 2 to get a determined value
        if(n == 1 || n == 2){
            return 1;
        }else{
            // Beginning with item 3, the result is the sum of the first two items
            return f(n - 1) + f(n - 2);
        }
    }
}

• Yang Hui Triangle

Yang Hui triangle is an interesting figure, a pyramid structure, the top and sides of the value fixed to 1, what should you think at this time?Yes, recursive exit!The values of the other parts are the sum of the two nearest values in the previous layer, for example, from top to bottom (Layer 4, Column 3), and their values are (Layer 3, Column 2)+ (Layer 3, Column 3).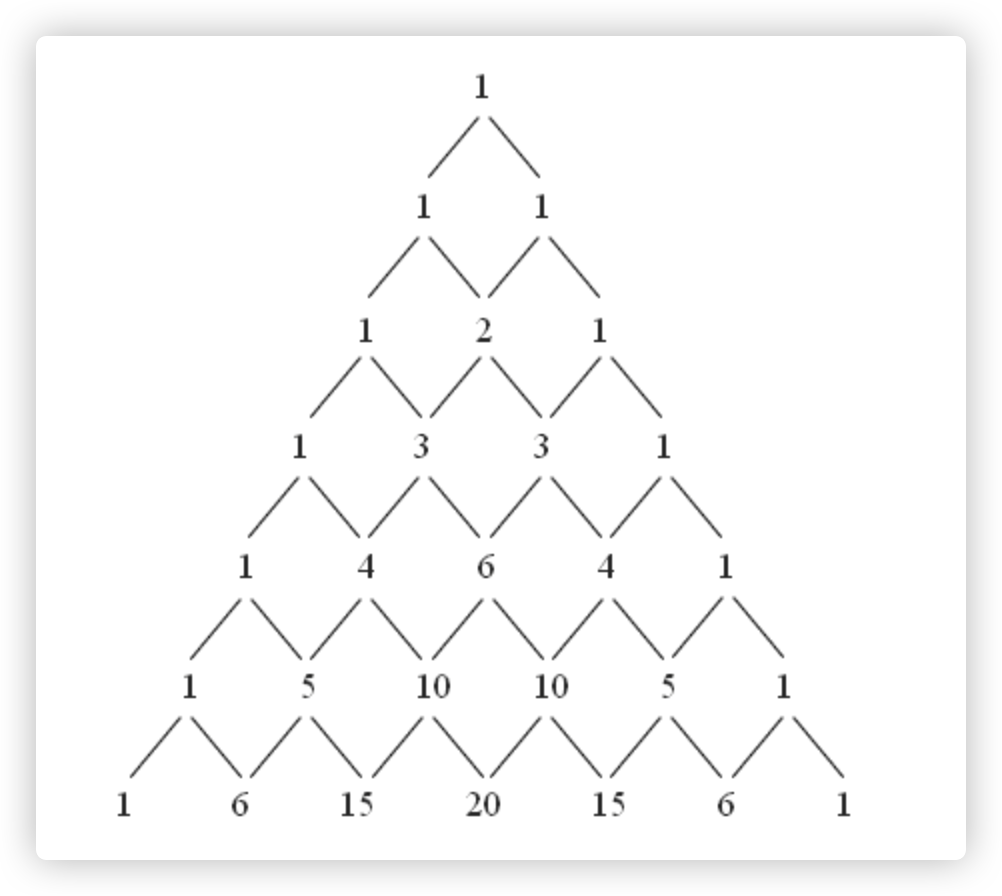

If we use the variable I to represent the layer and j to represent the column of that layer, then the value of (i, j) is (i-1, j-1)+ (i-1, j), what is this?Yes, a description of the rules!Finally, we just need to work out the criteria for recursive export, and we're done!From the composition above, we know that the number of elements in each layer will not exceed the number of layers in this layer and will be exactly equal, so do you know how the top and sides should be described?

public class Test{
    public static void main(String[] args){
        int i = 4;// Define a positive integer i
        int j = 3;// Define a positive integer j, no larger than i
        int result = getN(i,j);
        System.out.println(result);
    }
    public static int getN(int i,int j){
        // The values of the first and first columns are fixed to 1, and the values of the last column are also fixed to 1
        if(i == 1 || j == 1 || j == i){
            return 1;
        }else{
            // Use expressions to describe rules
            return getN(i - 1,j - 1) + getN(i - 1,j);
        }
    }
}

Think this is over?How come!Now that you have such a beautiful graphic, how can you relieve the itch without printing it out through a program?Unlike getting a single number, printing requires the number of layers you want to display, so we use a double for loop to build the entire graph:

public class Test{
    public static void main(String[] args){
        int n = 5;// Define a positive integer n
        print(n);
    }
    public static void print(int n){
        for(int i = 1;i <= n;i ++){
            // Insert spaces before each line, the number of spaces is related to the number of target layers
            for (int j = i;j <= n;j++){
                System.out.print(" ");
            }
            for (int j = 1;j <= i;j++){
                // Leave blank after output
                System.out.print(getN(i,j) + " ");
            }
            // Line Break After Printing One Layer
            System.out.println();
        }
    }
    public static int getN(int i,int j){
        // The values of the first and first columns are fixed to 1, and the values of the last column are also fixed to 1
        if(i == 1 || j == 1 || j == i){
            return 1;
        }else{
            // Use expressions to describe rules
            return getN(i - 1,j - 1) + getN(i - 1,j);
        }
    }
}

The results are as follows: