csdn turned around. I'm yzh myself, not copied articles
Note: this blog is written for beginners and does not use too many professional terms, so the description is very wordy, and the boss can give advice (this blog uses chain adjacency table to save the map)
Network flow knowledge is difficult. Please read it carefully

As the name suggests, network flow is an algorithm specially used to solve the network flow problem (also known as maximum flow)

Refer to Baidu Encyclopedia for specific definitions
The old rule is that you can't understand it with your mouth. It's better to analyze it through questions.
Luogu maximum network flow naked problem
Main idea of the title:
The source point and sink point are given, and the maximum network flow from source point to sink point is obtained. This seems to be the problem / mistake

Obviously, this problem can't be passed by violent dfs (then cut directly to the subject)

EK algorithm:

(this algorithm is relatively simple, but it also requires a period of careful thinking)
EK algorithm is the simplest and slowest algorithm in network flow, with a complexity of \ (O(nm^2) \)
This example is not easy to tell, so I made up a group myself

4 5 1 4
1 2 5
2 3 1
3 4 4
1 3 5
2 4 5

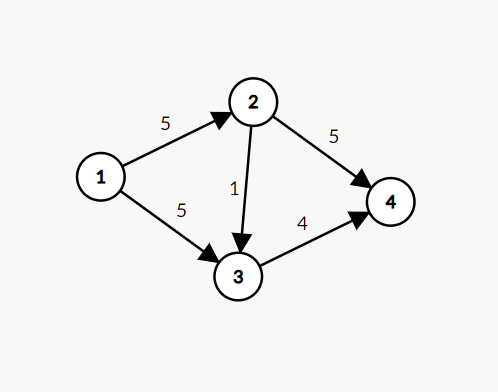
This picture has been like this since it was built. We can treat each side as a one-way pipe, with 1 as the source point and 4 as the sink point. Obviously, the output of this example is 9 (the road from 1 to 2 to 4 can dredge the water with the quantity of 5, and the road from 1 to 3 to 4 can dredge the water with the quantity of 4, because if the water with the quantity of 5 is dredged in 1 to 3, it will not go through 3 to 4, because the capacity of 3 to 4 is 4).
For network flow, the key point is to maintain the residual graph.
As the name suggests, residue means residue, that is, the remaining quantity. We call the difference between the maximum capacity MAXV of an edge and its actual flow F residue, that is

Residue \ (= MAXV − F \)

Then we take the residue as the weight of each edge and construct a graph called residue graph. If the weight is 0, it is equivalent to a break
Residual quantity map: (because the drawing website will overlap in two directions, so yzh you can only draw by hand)

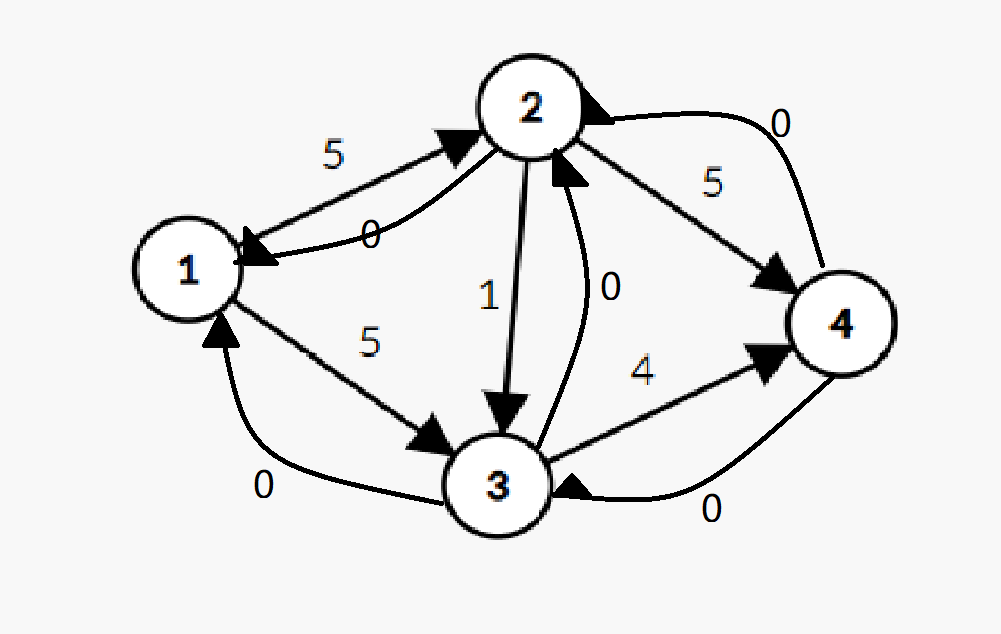
Someone will ask: is it useful to build an edge with an edge weight (pipe capacity) of 0? Of course, this reverse edge is used to allocate pipes for each road (Note: if the topic does not specify the pipe flow, the forward edge is the capacity and the reverse is 0. If the flow is given, the forward edge is the flow and the reverse is the capacity flow), For example:

The cgl teacher in a zb City wanted to lead the students to play csp, but found that three seats on the bus had been occupied. Then the cgl teacher discussed with the teacher and asked the teacher to refund the ticket.

This is not easy to say, so let's go through code analysis

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<queue>
using namespace std;
typedef long long ll;
const int N = 1010, M = 20010, INF = 1e9;
struct edge {
	int v, f, nxt;
};
edge e[M];
int head[N], d[N], pre[N];
bool st[N];
int cnt, n, m, s, t;
void add(int a, int b, int c) {
	e[cnt].v = b; e[cnt].f = c; e[cnt].nxt = head[a]; head[a] = cnt++;
	e[cnt].v = a; e[cnt].f = 0; e[cnt].nxt = head[b]; head[b] = cnt++;
}
bool bfs() {
	memset(st, 0, sizeof st);
	queue<int> q;
	q.push(s); st[s] = 1; d[s] = INF;
	while (q.size()) {
		int tmp = q.front(); q.pop();
		for (int i = head[tmp]; i != -1; i = e[i].nxt) {
			int ver = e[i].v;
			if (!st[ver] && e[i].f) {//Determine whether it conforms to the amplification path
				st[ver] = 1;
				d[ver] = min(d[tmp], e[i].f);
				pre[ver] = i; //Past the previous side 
				if (ver == t) return true;//We're at the meeting point
				q.push(ver);
			}
		}
	}
	return false;
}
ll EK() {
	ll res = 0;
	while (bfs()) {//bfs determines whether there is an amplification path
		res += d[t];
		for (int i = t; i != s; i = e[pre[i] ^ 1].v) {//Handle the flow of forward and reverse sides (described below)
			//e[pre[i]^1]. The v point of the v reverse side is the precursor node of the current point 
			e[pre[i]].f -= d[t];
			e[pre[i] ^ 1].f += d[t];
		}
	}
	return res;
}
int main() {
	memset(head, -1, sizeof head);
	cin >> n >> m >> s >> t;
	while (m--) {
		int a, b, c;
		cin >> a >> b >> c;
		add(a, b, c);
	}
	printf("%lld\n", EK());
	return 0;
}

Note: i^1 in the code is the number of the reverse side (you can prove it yourself)
We have just talked about the construction of the map. When the two-way edge is built, we need bfs to find the amplification path in the map.
As the name suggests, amplification means that if there is a path from the source point to the sink point, and the weight of any edge in the path is > 0, then the current state can be expanded as long as an amplification path with the existence of this path is found (judged by bfs), Then subtract the weight of the forward side passing through the path from the flow that can flow through the path (the minimum value of capacity), then add the weight of the reverse side to the flow, and add the answer to the flow (the initial state of the answer is 0), so as to get the final answer.
(this code is relatively simple, but it also requires a period of careful thinking)
Obviously, the complexity is \ (O(nm^2) \) and many problems can get stuck, so let's start learning the next algorithm with \ (O(n^2m) \) complexity

dinic:

(the idea of this algorithm is complex and may require careful thinking for a period of time)
Old rule, question 1
Problem of pilot pairing scheme for Logu P2756
Obviously, the mapping of this problem is a big difficulty. When the source point and sink point are not given in the problem, we usually set 0 as the source point and n+1 as the sink point (n+1 in this problem depends on the maximum data of the problem)
First, we connect the aircraft that can be matched with one side, then connect the foreign aircraft with the source point and the British aircraft with the sink point, and then connect the two aircraft if the two aircraft can be matched (the capacity of the side here can be set to 1).
The following is the drawing part:

int m, n, head[1010], tot=1, s, t, dep[1010], cur[1010];
bool vis[100010];
struct node
{
	int v, nt, w;
}edge[100010];
void add(int u, int v, int w) {
	edge[++tot] = { v,head[u],w };
	head[u] = tot;
	edge[++tot] = { u,head[v],0 };
	head[v] = tot;
}
int main() {
	memset(head, -1, sizeof(head));
	scanf("%d%d", &m, &n);
	s = 0;//Source point
	t = n + 1;//Meeting point
	while (1) {
		int u, v;
		scanf("%d%d", &u, &v);
		if (u == -1 && v == -1) break;
		add(u, v, 0x3f3f3f3f);
	}
	for (int i = 1; i <= m; ++i) {
		add(s, i, 1);
	}
	for (int i = m + 1; i <= n; ++i) {
		add(i, t, 1);
	}
	dinic();
	return 0;
}

After the drawing is completed, readers can try to use the EK algorithm. When submitting, they will find that T is lost,
So let's get to the point.
First, bfs is still used to judge whether there is an amplification path:

bool bfs() {
	queue<int> q;
	q.push(s);
	memset(dep, -1, sizeof(dep));
	dep[s] = 0;
	cur[s] = head[s];
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = head[u]; i; i = edge[i].nt) {
			int v = edge[i].v;
			cur[v] = head[v];
			if (dep[v] == -1 && edge[i].w) {
				dep[v] = dep[u] + 1;//Recording depth
				if (v == t) return true;
				q.push(v);
			}
		}
	}
	return false;
}

Here, in order to optimize the recording depth and prevent the next dfs from going backwards and increasing unnecessary complexity
Then we will talk about the operation of dfs (the old rule is to stick the code first):

int dfs(int u, int f) {
	if (u == t) {//Direct return upon arrival at the meeting point
		return f;
	}
	int dlt = 0;
	for (int i = cur[u]; i; i = edge[i].nt) {
		int v = edge[i].v;
		cur[u] = i;
		if (edge[i].w && dep[v] == dep[u] + 1) {
			int dt = dfs(v, min(f - dlt, edge[i].w));
			edge[i].w -= dt;
			edge[i ^ 1].w += dt;
			dlt += dt;
			//if (dlt == f) return f;
		}
	}
	if (!dlt) dep[u] = -1;
	return dlt;
}

In this dfs, the first parameter is the current node, the second f is to record the maximum flow so far, dlt is to record the used flow, the purpose of transmitting min(f - dlt, edge[i].w) is to maintain the residual diagram, dt is the maximum flow towards v, and then the dfs can add or subtract the weight. cur is something similar to pruning (not obvious in this problem)
dinic code is a little difficult to understand and needs some time to think
Output processing is not explained too much here. If you can't understand it, you can refer to the solution of Luogu problem.

#include<iostream>
#include<algorithm>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<functional>
#include<queue>
#pragma warning(disable:4996)
using namespace std;
int m, n, head[1010], tot=1, s, t, dep[1010], cur[1010];
bool vis[100010];
struct node
{
	int v, nt, w;
}edge[100010];
void add(int u, int v, int w) {
	edge[++tot] = { v,head[u],w };
	head[u] = tot;
	edge[++tot] = { u,head[v],0 };
	head[v] = tot;
}
bool bfs() {
	queue<int> q;
	q.push(s);
	memset(dep, -1, sizeof(dep));
	dep[s] = 0;
	cur[s] = head[s];
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = head[u]; i; i = edge[i].nt) {
			int v = edge[i].v;
			cur[v] = head[v];
			if (dep[v] == -1 && edge[i].w) {
				dep[v] = dep[u] + 1;
				if (v == t) return true;
				q.push(v);
			}
		}
	}
	return false;
}
int dfs(int u, int f) {
	if (u == t) {
		return f;
	}
	int dlt = 0;
	for (int i = cur[u]; i; i = edge[i].nt) {
		int v = edge[i].v;
		cur[u] = i;
		if (edge[i].w && dep[v] == dep[u] + 1) {
			int dt = dfs(v, min(f - dlt, edge[i].w));
			edge[i].w -= dt;
			edge[i ^ 1].w += dt;
			dlt += dt;
			//if (dlt == f) return f;
		}
	}
	if (!dlt) dep[u] = -1;
	return dlt;
}
void dinic() {
	int res = 0;
	while (bfs()) {
		res += dfs(s, 0x3f3f3f3f);
	}
	if (!res) {
		cout << "No Solution!";
		return;
	}
	printf("%d\n", res);
	int cnt = 0;
	for (int i = 2; i <= tot; i+=2) {
		if (edge[i].v != s && edge[i ^ 1].v != s)
			if (edge[i].v != t && edge[i ^ 1].v != t) {
				if (edge[i ^ 1].w != 0) {
					printf("%d %d\n", edge[i ^ 1].v, edge[i].v);
				}
			}
	}
}
int main() {
	memset(head, -1, sizeof(head));
	scanf("%d%d", &m, &n);
	s = 0;
	t = n + 1;
	while (1) {
		int u, v;
		scanf("%d%d", &u, &v);
		if (u == -1 && v == -1) break;
		add(u, v, 0x3f3f3f3f);
	}
	for (int i = 1; i <= m; ++i) {
		add(s, i, 1);
	}
	for (int i = m + 1; i <= n; ++i) {
		add(i, t, 1);
	}
	dinic();
	return 0;
}

I'll write about this first. I'll write about the minimum cut point and optimization when I have time. All OI guys remember to praise it