Network flow learning notes

Posted by matrixd on Mon, 24 Jan 2022 12:05:13 +0100

What is network flow?

Network flow is a kind of solution to the problem than water flow.

It can be understood that there is a flow network, and each side has a maximum carrying flow.

If the source point drains water desperately, find out how much water the final sink point can obtain.

Next, we will explain the network flow algorithm through several examples

P3376 [template] maximum network flow

Let's take the picture given in the title as an example:

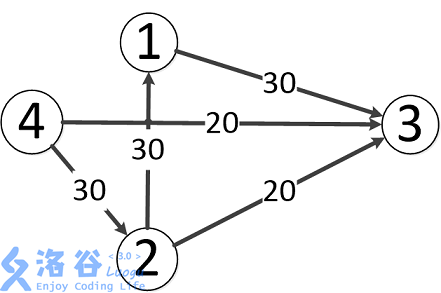
Let's first introduce a relatively simple algorithm:

\(\ tt{EK algorithm} \)

Pre cheese:

Flow: the flow of a path is the minimum value of the edge weight on the path
Maximum flow: the maximum flow that can be obtained by the sink point of one map
Augmented path: refers to another path from the source point to the sink point, and the traffic of this path is greater than that of the previously found path, then this path is called an augmented path

According to the concepts of augmented path and maximum flow, the maximum flow problem can be transformed into the problem of continuously solving augmented path. When the augmented path cannot be found in a graph, the maximum flow of the graph is found.

For the augmented path, we can continue to search from the source point through the edge with a weight greater than \ (0 \) until the sink point is found

The reason why we pass the edge whose weight is greater than \ (0 \) is that after we find an augmented Road, we subtract the minimum flow from the edge weight of the road. It is easy to prove that this is correct.

Find Zengguang Road Code:

inline bool bfs() {
	queue<int> q;
	memset(inque,false,sizeof(inque));
	memset(pre,-1,sizeof(pre));
	inque[s]=true;
	q.push(s);
	while(!q.empty()) {
		int u=q.front();
		q.pop();
		for(int i=head[u],v;i;i=edge[i].nxt) {
			v=edge[i].to;
			ll w=edge[i].w;
			if(!inque[v] && w) {
				pre[v].lst=u;
				pre[v].pos=i;
				if(v==t)
					return true;
				inque[v]=true;
				q.push(v);
			}
		}
	}
	return false;
}

The \ (pre \) array is used to record the precursor, \ (lst \) represents the precursor point, and \ (pos \) represents the precursor edge

Then we keep looking for the maximum flow and accumulate the flow

Code (wrong):

inline void EK() {
	while(bfs()) { // Keep looking for Zengguang road
		ll flow=inf;
		for(int i=t;i!=s;i=pre[i].lst)
			flow=min(flow,edge[pre[i].pos].w); // Calculated flow
		for(int i=t;i!=s;i=pre[i].lst)
			edge[pre[i].pos].w-=flow; // Subtract the flow to facilitate the calculation of Zengguang road
		ans+=flow; // Cumulative flow
	}
}

Why is this wrong

Let's look at this picture

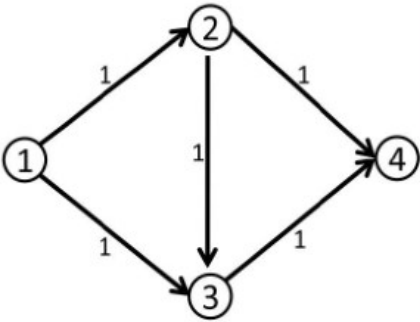
If the augmented path found for the first time is \ (1 \to 2 \to 3 \to 4 \), then the augmented path will not be found after that, and the maximum flow obtained is \ (1 \). Obviously, the maximum flow of this graph is \ (2 \), and this answer is wrong.

We introduce a concept of reverse edge, that is, when each edge is built, another reverse edge with edge weight \ (0 \) is built.

Now the diagram of the finished edge is as follows:

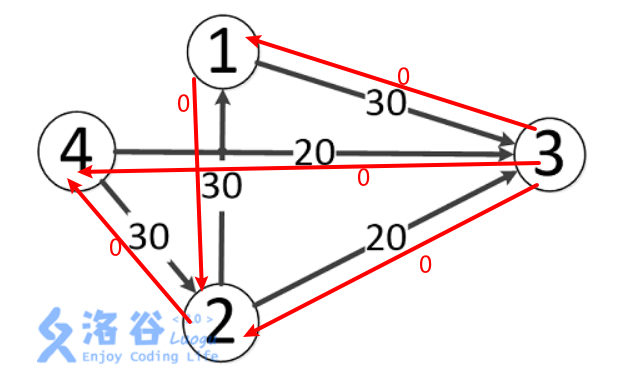
After finding an augmented path, we subtract the minimum flow from the edge weights on this edge, and add the minimum flow to the edge weights on the opposite edge of this edge

What's the point?

This is equivalent to one more estoppel operation.

For example, we first find an augmented path (non example) with \ (1 \to 2 \to 4 \to 6 \), and use the reverse edge to find that the point of \ (4 \) can directly reach \ (3 \), so we can use the reverse edge to change this path.

Therefore, the reverse side is to make a mark, so that the later Zengguang road has the opportunity to change the previous Zengguang Road, so as to ensure the correctness of the answer.

Complete code of this question:

#include <queue>
#include <cstdio>
#include <cstring>
#define min(a,b) ((a)<(b)?(a):(b))
typedef long long ll;
using namespace std;
const ll inf=1e18;
const int N=2e2+7,M=5e3+7;

struct Edge {
	int nxt,to;
	ll w;
}edge[M<<1];

struct Pre {
	int lst,pos;
}pre[N];

int head[M<<1],tot=1;
bool inque[N];

ll ans;
int n,m,s,t;

inline void AddEdge(int u,int v,ll w) {
	edge[++tot].nxt=head[u];
	edge[tot].to=v;
	edge[tot].w=w;
	head[u]=tot;
}

inline bool bfs() {
	queue<int> q;
	memset(inque,false,sizeof(inque));
	memset(pre,-1,sizeof(pre));
	inque[s]=true;
	q.push(s);
	while(!q.empty()) {
		int u=q.front();
		q.pop();
		for(int i=head[u],v;i;i=edge[i].nxt) {
			v=edge[i].to;
			ll w=edge[i].w;
			if(!inque[v] && w) { // ! inque[v] is used to judge the ring whose edge weight sum is 0
				pre[v].lst=u;
				pre[v].pos=i; // Record Zengguang Road
				if(v==t) // Find Zengguang road and return
					return true; 
				inque[v]=true;
				q.push(v);
			}
		}
	}
	return false;
}

inline void EK() {
	while(bfs()) { // Keep looking for Zengguang road
		ll flow=inf;
		for(int i=t;i!=s;i=pre[i].lst)
			flow=min(flow,edge[pre[i].pos].w); // Calculated flow
		for(int i=t;i!=s;i=pre[i].lst) {
			edge[pre[i].pos].w-=flow; // Subtract the flow to facilitate the calculation of Zengguang road
			edge[pre[i].pos^1].w+=flow;
		}
		ans+=flow; // Cumulative flow
	}
}

signed main() {
	scanf("%d%d%d%d",&n,&m,&s,&t);
	for(int i=1,u,v;i<=m;++i) {
		ll w;
		scanf("%d%d%lld",&u,&v,&w);
		AddEdge(u,v,w);
		AddEdge(v,u,0);
	}
	EK();
	printf("%lld",ans);
    return 0;
}

P3381 [template] minimum cost maximum flow

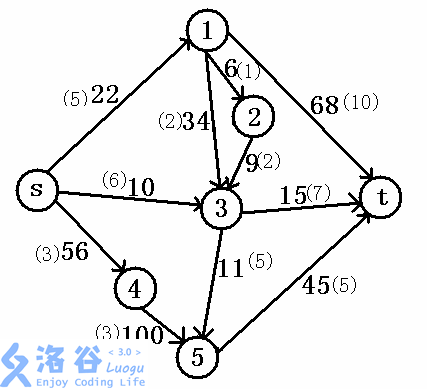
(in fact, it is the maximum current + the shortest circuit

How?

Very simple, just change BFS to SPFA

Note that the cost of the reverse side is the opposite of that of the forward side, because you have to refund when you return!!!

Therefore, there is a negative edge weight, which is more convenient to use SPFA

Full code:

#include <queue>
#include <cstdio>
#include <cstring>
#define min(a,b) ((a)<(b)?(a):(b))
typedef long long ll;
using namespace std;
const int inf=0x3f3f3f3f;
const int N=5e3+7,M=5e4+7;

struct Edge {
	int nxt,to;
	int w,price;
}edge[M<<1];

struct Pre {
	int lst;
	int pos;
}pre[N];

int head[N];
int dis[N];
bool inque[N];

int n,m,s,t;
int tot=1,ans,cost;

inline void AddEdge(int u,int v,int w,int p) {
	edge[++tot].nxt=head[u];
	edge[tot].to=v;
	edge[tot].w=w;
	edge[tot].price=p;
	head[u]=tot;
}

inline bool SPFA() { // Finding the least expensive augmented path with SPFA
	memset(pre,0,sizeof(pre));
	memset(dis,inf,sizeof(dis));
	memset(inque,false,sizeof(inque));
	queue<int> q;
	q.push(s);
	inque[s]=true;
	dis[s]=0;
	while(!q.empty()) {
		int u=q.front();
		q.pop(),inque[u]=false;
		for(int i=head[u],v,p;i;i=edge[i].nxt) {
			v=edge[i].to,p=edge[i].price;
			if(edge[i].w>0 && dis[v]>dis[u]+p) {
				dis[v]=dis[u]+p;
				pre[v].lst=u;
				pre[v].pos=i;
				if(!inque[v]) {
					q.push(v);
					inque[v]=true;
				}
			}
		}
	}
	return dis[t]!=inf;
}

inline void EK() {
	while(SPFA()) {
		int minn=inf;
		for(int i=t;i!=s;i=pre[i].lst)
			minn=min(minn,edge[pre[i].pos].w);
		for(int i=t;i!=s;i=pre[i].lst) {
			edge[pre[i].pos].w-=minn;
			edge[pre[i].pos^1].w+=minn;
		}
		ans+=minn;
		cost+=minn*dis[t];
	}
}

signed main() {
	scanf("%d%d%d%d",&n,&m,&s,&t);
	for(int i=1,u,v,w,p;i<=m;++i) {
		scanf("%d%d%d%d",&u,&v,&w,&p);
		AddEdge(u,v,w,p);
		AddEdge(v,u,0,-p); // Pay attention to edge construction
	}
	EK();
	printf("%d %d",ans,cost);
    return 0;
}

In fact, Dijkstra can also be used. Just change it when building edges. It is suggested to learn from Johnson

Next, we introduce a new algorithm:

\(\ tt{Dinic algorithm} \)

Let's first look at the shortcomings of EK algorithm?

Obviously, the EK algorithm can only find augmented paths one by one. Do we have an algorithm that can find many at a time?

Dinic algorithm can realize multi-channel augmentation, which is divided into two steps: bfs layering + dfs augmentation

In Dinic algorithm, our bfs layers each point, that is, the minimum number of points from the source point to each point.

code:

inline bool bfs() {
	queue<int> q;
	memset(deep,0,sizeof(deep));
	q.push(s);
	deep[s]=1;
	while(!q.empty()) {
		int u=q.front();
		q.pop();
		for(int i=head[u],v;i;i=edge[i].nxt) {
			v=edge[i].to;
			if(!deep[v] && edge[i].w) {
				deep[v]=deep[u]+1;
				q.push(v);
			}
		}
	}
	return deep[t];
}

Next, we use dfs to augment

code:

inline ll dfs(int u,ll flow) {
	if(u==t)
		return flow;
	ll outflow=0;
	for(int i=head[u],v;i && flow;i=edge[i].nxt) {
		v=edge[i].to;
		ll w=edge[i].w;
		if(w && deep[v]==deep[u]+1) {
			ll res=dfs(v,min(flow,w));
			edge[i].w-=res;
			edge[i^1].w+=res;
			flow-=res;
			outflow+=res;
		}
	}
	if(!outflow) // If this point cannot continue to transmit to the sink point, it is not necessary to pass through this point and mark this point
		deep[u]=0;
	return outflow;
}

Why is there a line of deep[v]==deep[u]+1 in the code?

At this time, the role of layering is reflected. With this line, we can ensure that we are looking for the shortest widening road, which greatly shortens the number of times we return and look again

Current arc optimization

We add a \ (cur \) array, which is somewhat similar to the \ (head \) array of the adjacency table. It will be modified with dfs

Every time we find an edge, we modify the \ (cur \) array to change the number of the edge, in other words, the edge we pass will not go

Principle: when we are in dfs, the edge we traverse first must have been widened (or cannot continue to be widened), and this edge is useless. We use the \ (cur \) array to discard these useless edges, and the efficiency will be greatly improved.

Of course, we can also use arc optimization when using EK algorithm to calculate the cost flow.