Niuke Xiaobai monthly race 34

Question A (dd love science 1.0)

Title Link

Title Description

Recently, the great scientist dd is studying transgenic Chinese cabbage. The gene sequence of Chinese cabbage is composed of a string of capital English letters. After rigorous reasoning, dd found that only when the gene sequence of Chinese cabbage is in a non decreasing form, the high added value of this Chinese cabbage will reach the highest, so the excellent dd began to modify the gene sequence of Chinese cabbage, The cost for dd to modify any position of the gene sequence every time is 1. dd wants to know what is the minimum cost to modify the gene sequence of Chinese cabbage to maximize its high added value.

Topic analysis

Modify the minimum characters to make the whole string the longest non decreasing string.

Problem solving ideas

1. Create two character arrays (a,b): a array stores the original string, and B array stores the updated longest non decreasing string.
2. Assign the first character of array a to b first; Traverse the original array. If the elements of array a are larger than those of array b, assign the elements of array a to b; Otherwise, find the array subscript m of the first element greater than a[i] in the b array, and assign a[i] to b[m].
3. Finally, the answer is to subtract the number of elements in array b from the number of elements in array a by the original length.

code implementation

#include<bits/stdc++.h>
using namespace std;
char a[1000010],b[1000010];
int n,m,ans=1;
int main(){
    cin>>n>>a;
    b[ans]=a[0];
    for(int i=1;i<n;i++)
        if(b[ans]<=a[i]) b[++ans]=a[i];
        else m=upper_bound(b+1,b+ans+1,a[i])-b,b[m]=a[i];
    cout<<n-ans<<endl;
    return 0;
}

Question E (dd love rotation)

Title Link

Title Description

Read in an n*n matrix. There are two operations for a matrix
1: Clockwise needle rotation 180 ° 180° 180°
2: About row mirroring
as
[ 1 2 3 4 ] \left[ \begin{matrix} 1 & 2 \\ 3 & 4\\ \end{matrix} \right] [13] 24] become [ 3 4 1 2 ] \left[ \begin{matrix} 3 & 4 \\ 1 & 2\\ \end{matrix} \right] [31​42​]
Give q operations and output the matrix after operation

Topic analysis

Find the matrix of n*n after q times of transformation operation

Problem solving ideas

1. The matrix can actually be divided into two parts by rotating 180 ° clockwise: up and down and left and right.
The mirror operation of a matrix is actually the up and down flip of the matrix. So first define two functions: the function of flipping up and down and the function of flipping left and right.
2. Because the matrix obtained by either 1 operation or c operation is the same; The even number of 1 operations or even number of 2 operations are the same as the original matrix.

For example:

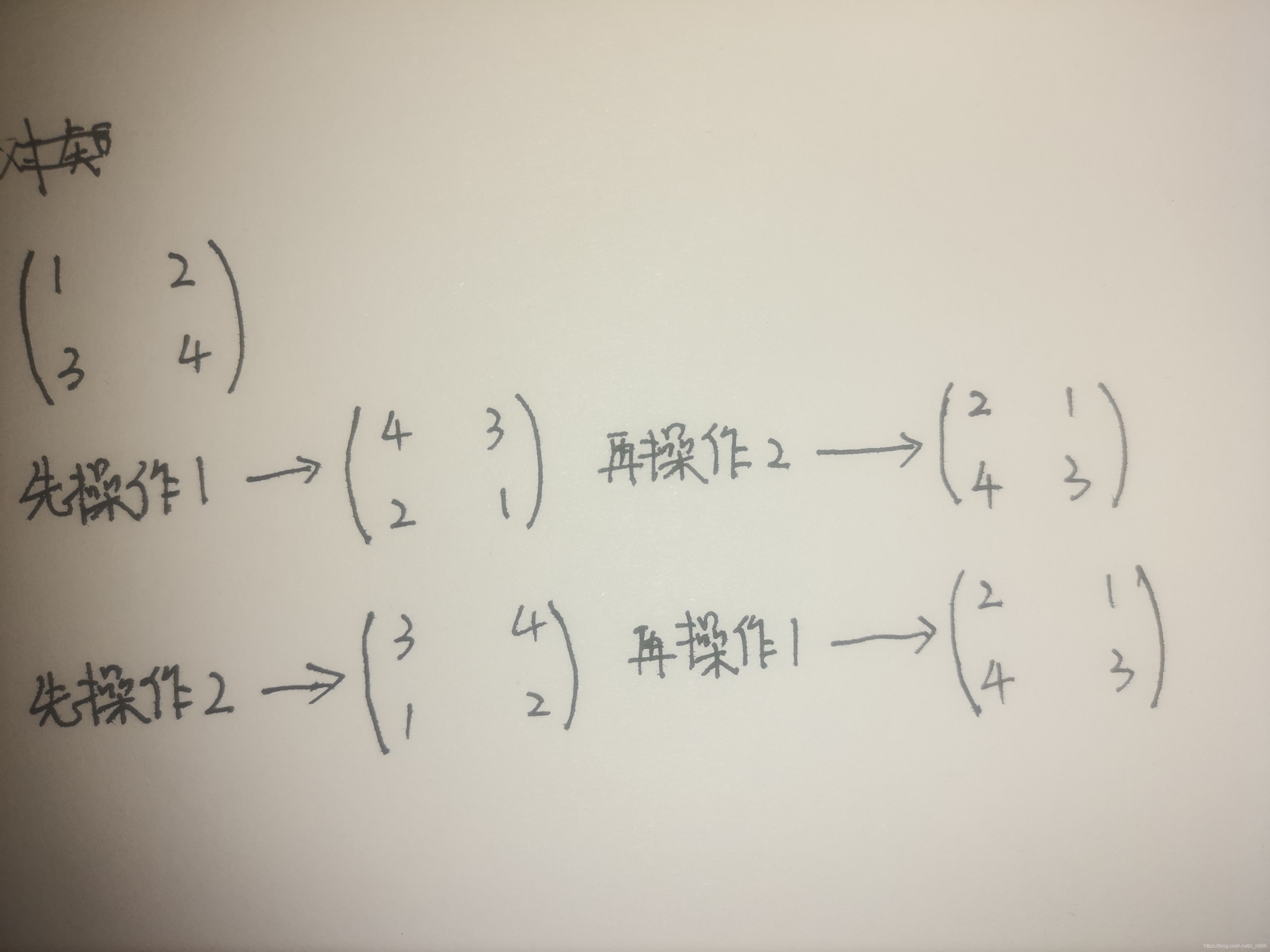
3. Based on the analysis of 2, only the different matrix operations of q operations need to be counted one by one, and then the corresponding operation is carried out when the modulus of 2 is equal to 1; Equal to 0 does not operate.

code implementation

#include<bits/stdc++.h>
using namespace std;
int a[10010][10010];
int n,m,op,p,q;
void fun1(){
    for(int i=0;i<n;i++)for(int j=0;j<n/2;j++) swap(a[j][i],a[n-j-1][i]);
}
void fun2(){
    for(int i=0;i<n;i++)for(int j=0;j<n/2;j++) swap(a[i][j],a[i][n-j-1]);
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++)for(int j=0;j<n;j++)cin>>a[i][j];
    cin>>m;
    for(int i=0;i<m;i++){
        cin>>op;
        if(op==1)p++;
        else q++;
    }
    if(p%2==1)fun1(),fun2();
    if(q%2==1)fun1();
    for(int i=0;i<n;i++){for(int j=0;j<n;j++){cout<<a[i][j]<<" ";}cout<<endl;}
    return 0;
}

Question F (dd love box)

Title Link

Title Description

Read in N, x and give n numbers a [ 1 ] , a [ 2 ] , ... ... , a [ n ] a[1],a[2],......,a[n] a[1],a[2],..., a[n], find the minimum interval [ l , r ] [l,r] [l,r], make a [ l ] + a [ l + 1 ] + ... ... + a [ r ] ≥ x a[l]+a[l+1]+......+a[r]≥x a[l]+a[l+1] +... + a[r] ≥ x, if there is an interval of the same length, the one with the smallest L is output

Topic analysis

Find the minimum interval where the sum of all interval values is greater than the given length

Problem solving ideas

If violence is used, it must blow up, so prefix and + dichotomy are used for optimization.
1. Use an array to store the prefix and of the array in the main function.
2. Establish a check function to find the minimum interval.
3. Search rules: traverse the prefix and array, search from the ith to the nth, first find the middle value mi of in, and compare the sum size between IMIS. If the sum is greater than the given value, the interval will be reduced, search again, and update the smallest value; If it is smaller than the given value, expand the interval to find the update again.
Note: CPP IOS:: sync is required when using CIN_ with_ stdio(false); cin. tie(0); Accelerate the input, or it may explode.

code implementation

#include<bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
typedef long long ll;
int n,m,k,l,r,c,r0,l0,mi;
ll sum[10000010];
void check(int a,int b){
    l0=inf,r0=inf+inf;
    for(ll i=1;i<=a;i++){
        l=i,r=a,c=inf;
        while(l<=r){
            mi=(l+r)>>1;
            if(sum[mi]-sum[i-1]>=b)r=mi-1,c=min(c,mi);
            else l=mi+1;
        }
        if(c-i<r0-l0)l0=i,r0=c;
    }
    cout<<l0<<" "<<r0<<endl;
}
int main(){  
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin>>n>>m;
    for(ll i=1;i<=n;i++)cin>>k,sum[i]=sum[i-1]+k;
    check(n,m);
    return 0;
}

Question H (dd love neat)

Title Link

Title Description

dd thinks that a neat kk infinite sequence should satisfy the following conditions
If k=1... ABAB
When k=2... Abbabbabbabbab
When k=3... Abbbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbabbab
k finite sequence is any continuous subsequence of k infinite sequence
And so on, where a,ba,b are positive integers and a ≥ ba ≥ b
as [ 2 , 1 , 1 , 1 , 2 ] ， [ 6 , 10 , 6 ] [2,1,1,1,2]，[6,10,6] [2,1,1,1,2] and [6,10,6] can be considered as a legal K-Finite sequence with k=3
Now I'll give you a sequence c c c. It is not necessarily a kk finite sequence, so you can modify the sequence
For each correction, you can select a location i ( 1 ≤ i ≤ n ) i(1≤i≤n) i(1 ≤ i ≤ n), put c [ i ] c[i] c[i] becomes c [ i ] − 1 c[i]-1 c[i] − 1, ask the minimum number of corrections required to turn the sequence into a k-Finite sequence

Topic analysis

The number of times to modify an array into an array of the specified format

Problem solving ideas

In the obtained rule sequence, i takes the remainder of k+1, the positions of the remainder are equal, and they are all equal to a. The value of a should be the smallest value in these positions (because addition cannot be performed, only subtraction can be performed). because a ≥ b a≥b A ≥ b, traverse the original array a, and find the minimum change by using prefix sum.

code implementation

/*
  Stored information for each array:
  a Array: original array; b array: the minimum value in the original array
  c Array: the sum of each k position of the original array; d array: the position of K in the original array
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[10000010],b[10000010],c[10000010],d[10000010],s,p;
ll ans=1e18+11;
int n,m;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin>>n>>m; m++;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=0;i<m;i++) b[i]=1000000001;
    for(int i=1;i<=n;i++)c[i%m]+=a[i];
    for(int i=1;i<=n;i++)b[i%m]=min(b[i%m],a[i]);
    for(int i=1;i<=n;i++)d[i%m]++; s=a[1];
    for(int i=2;i<=n;i++)s=min(s,a[i]);
    for(int i=1;i<=n;i++)p+=a[i];
    for(int i=0;i<m;i++) ans=min(ans,c[i]-b[i]*d[i]+p-c[i]-(1ll*n-d[i])*s);
    cout<<ans<<endl;
    return 0;
}