Did you write this because 2021.7.10 biweekly match of force buckle The fourth question was written with memorization + deep search, but there have been several examples that can't pass. I saw another question solution when I was troubled Why can't mnemonic search get a positive solution? It dawned on me. I hereby make a record

No aftereffect. The so-called non aftereffect means that for a given stage state, the state of its previous stages cannot directly affect its future decision-making.

Title Description:

 

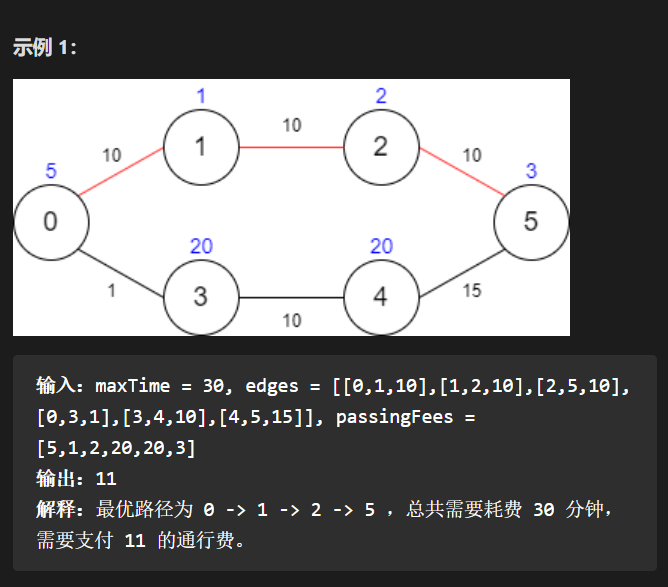
Competition idea:

The graph is represented by an adjacency table. g[i] = {p0,...,p_j} the point adjacent to point I is {p0,...,p_j}

gg[i][j] to represent the time overhead between point I and point j

dp[curp][curtime] the minimum cost of reaching the destination when the point curp has been used

Then: DP [0] [0] = max {DP [J] [GG [0] [J]} go down and search deeply

There seems to be no problem, but:

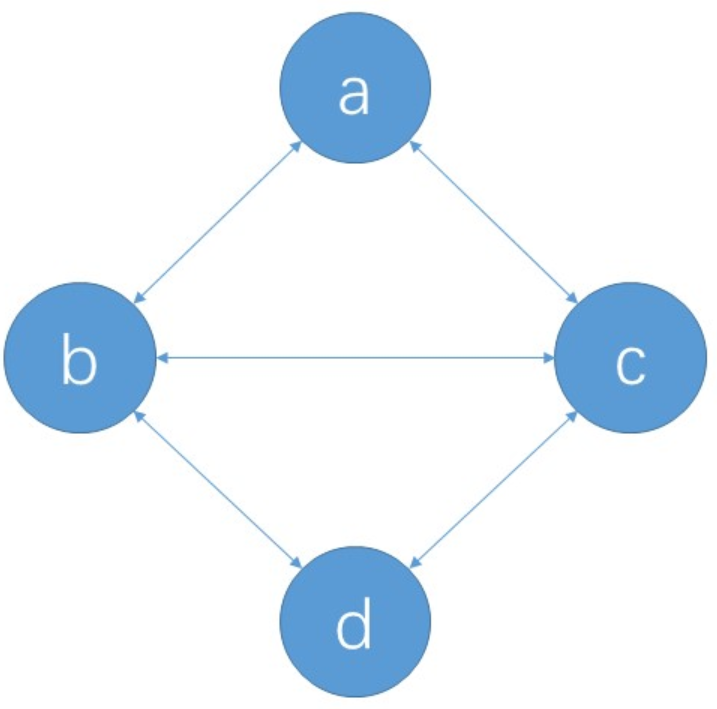
For such a deep search of a - > D

(1) Starting from a, access B, then access c and d. the actual access paths are a - > b - > d and a - > b - > c - > d
(2) Access c from a and directly return memo[c]. The actual access path is a - > c - > D

It is not difficult to find that the access path is missing a - > C - > b - > D. why?

The reason is that in (1), the memo[c] calculated when accessing c from B is not the maximum probability from c to d. There are two paths from c to D: c - > D and c - > b - > D. since B will be marked as accessed, it is impossible to go from c to B, so the correctness of memo[c] cannot be guaranteed. Furthermore, the above process does not meet the non aftereffect in dynamic programming. The so-called non aftereffect means that for a given stage state, the state of its previous stages cannot directly affect its future decision-making.

Therefore, even if I set the two dimensions dp[curp][curtime], if there are two paths to the point of curp, the time is curtime, such as the point c in the above figure, then the point c is not necessarily the smallest. Because there are precursor values to limit it, the correctness of this method cannot be guaranteed, that is, the aftereffect of dynamic programming cannot be guaranteed

Game code:

#define x first
#define y second
#include <iostream>
#include <bits/stdc++.h>
#include <ctime>
#include <algorithm>
#include <stdlib.h>
using namespace::std;
using LL = long long;
using PII = pair<int,int>;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int dir[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
class Solution {
public:
    vector<vector<int>> g;
    int n;
    int dp[1005][1005];// DP [i] minimum cost from I to n - 1 - 1 indicates unreachable
    int maxTime;
    bool vi[1005];
    int gg[1005][1005];
    int dfs(int curtime,int curp,vector<int>& pf) {
        if(dp[curp][curtime] != INF) {
            return dp[curp][curtime];
        }// If you've asked before
        if(curp == n - 1) {
            return pf[n - 1];
        }
        int res = INF;
        for(auto& next : g[curp]) {
            if(!vi[next]) {
                if(curtime + gg[curp][next] > maxTime) continue;
                vi[next] = true;
                int t = dfs(curtime + gg[curp][next],next,pf);
                if(t != -1)
                    res = min(res,t);
                vi[next] = false;
            }
        }
        if(res != INF)
            res += pf[curp];
        dp[curp][curtime] = res == INF ? -1 : res;
        return dp[curp][curtime];
    }
    int minCost(int maxTime_, vector<vector<int>>& edges, vector<int>& pFees) {
        n = pFees.size();
        g.resize(n);
        maxTime = maxTime_;
        // initialization
        for(int i = 0;i < n;i ++) {
            memset(dp[i],INF,4 * 1005);
            vi[i] = false;
            memset(gg[i],-1,4 * n);
        } 
        for(auto& e : edges) {
            if(gg[e[0]][e[1]] == -1) {
                g[e[0]].push_back(e[1]);
                g[e[1]].push_back(e[0]);
                gg[e[0]][e[1]] = e[2];
                gg[e[1]][e[0]] = e[2];
            } else {
                gg[e[0]][e[1]] = min(gg[e[0]][e[1]],e[2]);
                gg[e[1]][e[0]] = gg[e[0]][e[1]];
            }
            
        }
        vi[0] = true;
        int t = dfs(0,0,pFees);
        return t;
    }
};

Correct code:

// author : wyx
#define x first
#define y second
#include <iostream>
#include <bits/stdc++.h>
#include <ctime>
#include <algorithm>
#include <stdlib.h>
using namespace::std;
using LL = long long;
using PII = pair<int,int>;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int dir[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
class Solution {
public:
    vector<vector<int>> g;// Adjacency table
    int n;// Number of points
    int dp[1005][1005];// -1 means unreachable
    // dp[i][j] at j, the minimum cost when the total time is I
    int gg[1005][1005];// Distance between two points
    int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& ps) {
        n = ps.size();
        g.resize(n);
        // initialization
        for(int i = 0;i < n;i ++) {
            memset(dp[i],-1,4 * 1005);
            memset(gg[i],-1,4 * n);
        }
        // Initialization diagram
        for(auto& e : edges) {
            if(gg[e[0]][e[1]] == -1) {
                g[e[0]].push_back(e[1]);
                g[e[1]].push_back(e[0]);
                gg[e[0]][e[1]] = e[2];
                gg[e[1]][e[0]] = e[2];
            } else {
                gg[e[0]][e[1]] = min(gg[e[0]][e[1]],e[2]);
                gg[e[1]][e[0]] = gg[e[0]][e[1]];
            }
            
        }
        for(int i = 0;i <= maxTime;i ++) dp[0][i] = ps[0];
        for(int t = 0;t <= maxTime;t ++) {
            for(int j = 0;j < n;j ++) {
                if(dp[j][t] != -1) {
                    // Explain that you can reach point j at time t and then transfer from j
                    for(auto& next : g[j]) {
                        if(gg[next][j] + t > maxTime) continue;
                        if(dp[next][t + gg[next][j]] == -1 || \
                        dp[next][t + gg[next][j]] > dp[j][t] + ps[next]) {
                            dp[next][t + gg[next][j]] = dp[j][t] + ps[next];
                        }
                    }
                }
            }
        }
        return dp[n - 1][maxTime];
    }
};

Competition summary:

We should understand more about dynamic programming and more about non special effects, so as to better understand and apply dynamic programming: D