Northwest University of technology NOJ-Python programming problem set:
Noj Python Programming: Season 1: season 1-easy (1-10)
Noj Python Programming: Season 2: Season 2 snippet (11-20)
Noj Python Programming: Season 3: season 3-loop (21-30)
NOJ-Python programming: Season 4: enumeration algorithm (31-40)
NOJ-Python programming: Season 5: modularization (41-50)
Noj Python Programming: Season 6: season 6-string (51-60)
NOJ-Python programming: Season 7: season 7-list and tuple (61-70)
Noj Python Programming: Season 8: season 8-sets and Dictionary (71-80)
Noj Python Programming: Season 9: class (81-90)
Noj Python Programming: Season 10: Season 10 challenges (91-100)
Season 4: season 4-enumeration algorithm (31-40)
Pre knowledge points
It is recommended to understand the basic application of the following function library before completing the topic.
Basic operators: (from rookie tutorial)
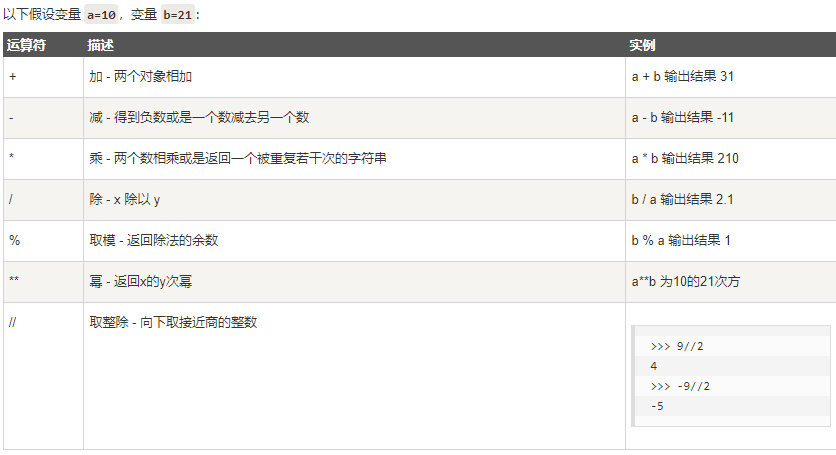
Pay attention to the difference between / and / /
Two dimensional array
python is a little troublesome to define a two-dimensional array:
a=[[0 for i in range(1000+5)] for i in range(1000+5)] defines a a [ ] [ ] a[][] a [] [] size is (1005 * 1005) and the initial value is 0
math.gcd
- Syntax: math gcd(x,y)
- Returns the maximum common divisor of integers x,y
Line up to cross the river

The stone pier and lotus leaf may be analyzed according to the meaning of the topic. In order to maintain the queue order, there are at most 2 frogs in a stone pier and n lotus leaves. In addition, there is a starting point. The answer is 2 n ∗ ( m + 1 ) 2^n*(m+1) 2n * (m+1), in fact, you can also look at the data to find the law and find this formula.
def qpow(a,b):
a,ans=a,1
while b!=0:
if b&1:
ans=(ans*a)
b>>=1
a=(a*a)
return ans
pass
while 1:
n,m=map(int,input().split(','))
if(n==-1 and m==-1):
break
ans=qpow(2,n)*(m+1)
print(ans)
# Code By Phoenix_ZH
division algorithm
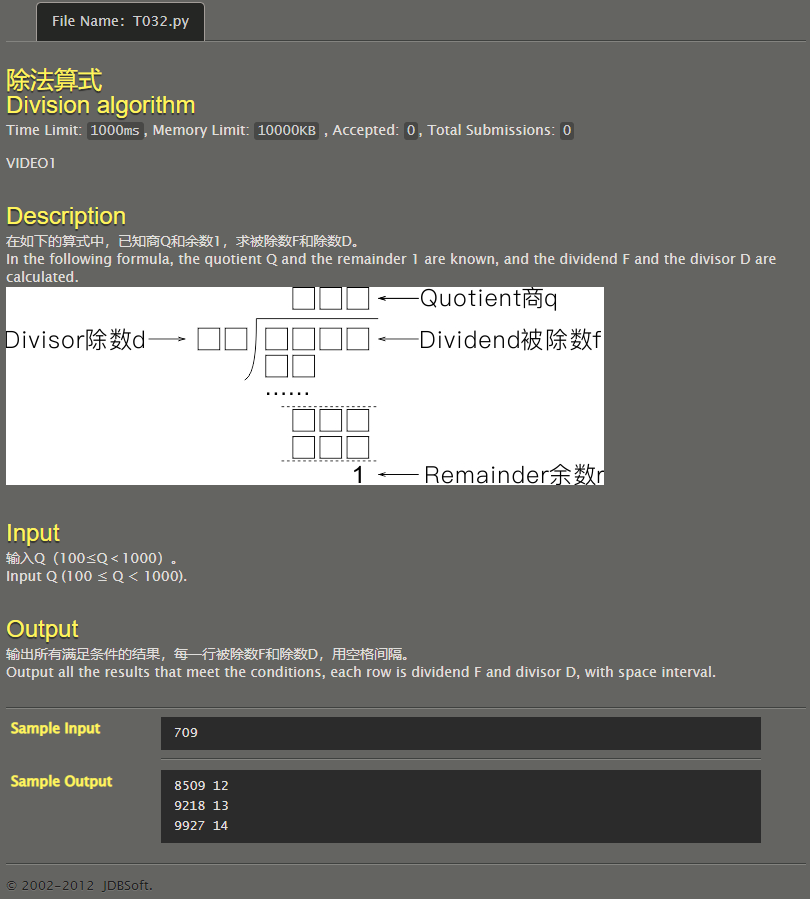
At first, I thought it was a wrong question, and the results were more than the output. But the picture observed: the number before the last remaining 1 is 3 digits! Then you can enumerate the divisor and divisor.
q=int(input())
for i in range(1000,9999+1):
for j in range(10,99+1):
if(i//J = = q and I% J = = 1 and (Q% 10) * J > = 100): # note that three digits must be left before the remainder, so make a judgment
print(i,j,sep=' ')
# Code By Phoenix_ZH
Chang'an
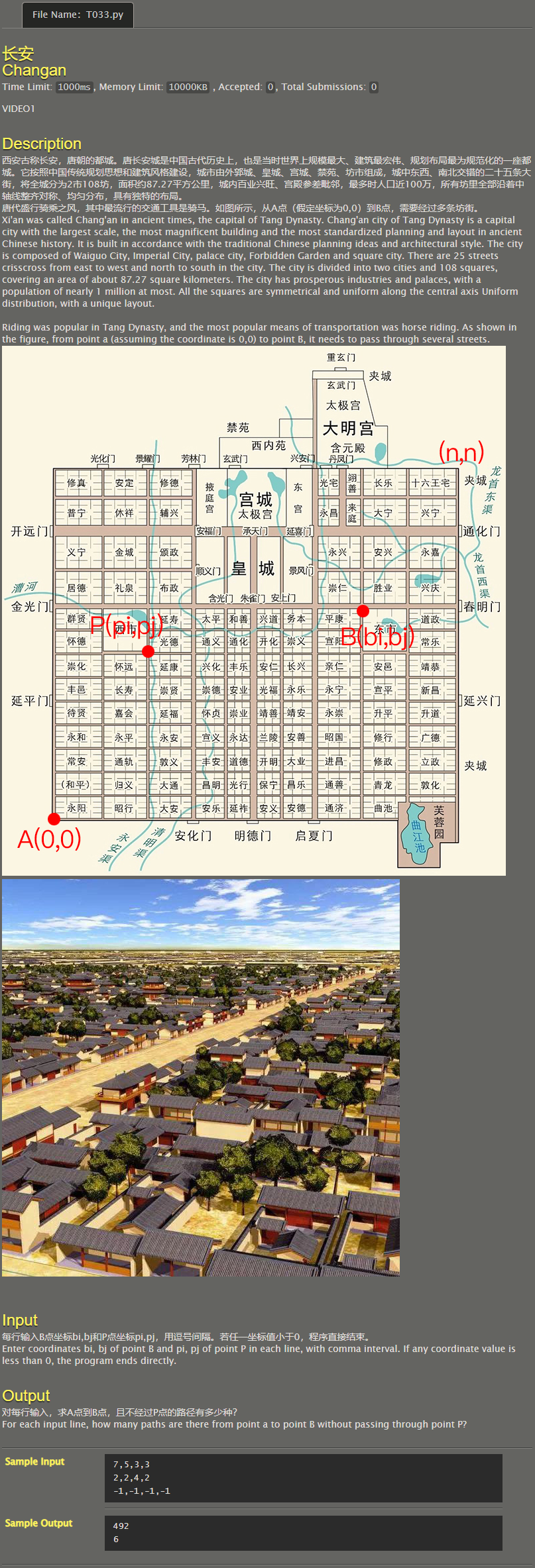
What if you don't consider point P?
spot ( x , y ) (x,y) (x,y) can be represented by points ( x − 1 , y ) (x-1,y) (x − 1,y) or point ( x , y − 1 ) (x,y-1) (x,y − 1) is obtained.
use d p [ x ] [ y ] dp[x][y] dp[x][y] indicates the point of arrival ( x , y ) (x,y) The number of schemes of (x,y), then the starting point ( 0 , 0 ) (0,0) The number of schemes of (0,0) is 1, i.e d p [ 0 ] [ 0 ] = 1 dp[0][0]=1 DP [0] [0] = 1 (it is at the starting point at the beginning, so it is 1)
that d p [ x ] [ y ] = d p [ x − 1 ] [ y ] + d p [ x ] [ y − 1 ] dp[x][y]=dp[x-1][y]+dp[x][y-1] dp[x][y]=dp[x − 1][y]+dp[x][y − 1]) (if point ( x , 0 ) (x,0) (x,0) or ( 0 , y ) (0,y) (0,y) then there is only one transfer method)
What about the condition of adding point P?
Then make sure ( x , y ) (x,y) (x,y) the previous node is not a point ( p i , p j ) (p_i,p_j) (pi, pj) just fine.
But in order to transfer equation unification: guarantee d p [ p i ] [ p j ] permanent by 0 Just good Yes dp[p_i][p_j] is always 0 If dp[pi] [pj] is constant to 0, the rest is consistent with the case without considering p.
#Recurrence:
while 1:
tx,ty,px,py=map(int,input().split(","))
if(tx==-1 and ty==-1 and px==-1 and py==-1):
break
dp=[[0 for i in range(1000+5)] for i in range(1000+5)]
dp[0][0]=1
for i in range(tx+1):
for j in range(ty+1):
if((i==0 and j==0)or(i==px and j==py)):
continue
if(i-1>=0):
dp[i][j]+=dp[i-1][j]
if(j-1>=0):
dp[i][j]+=dp[i][j-1]
# print(i,j,dp[i][j])
print(dp[tx][ty])
'''
10,10,5,5
121252
'''
# Code By Phoenix_ZH
Lay the floor
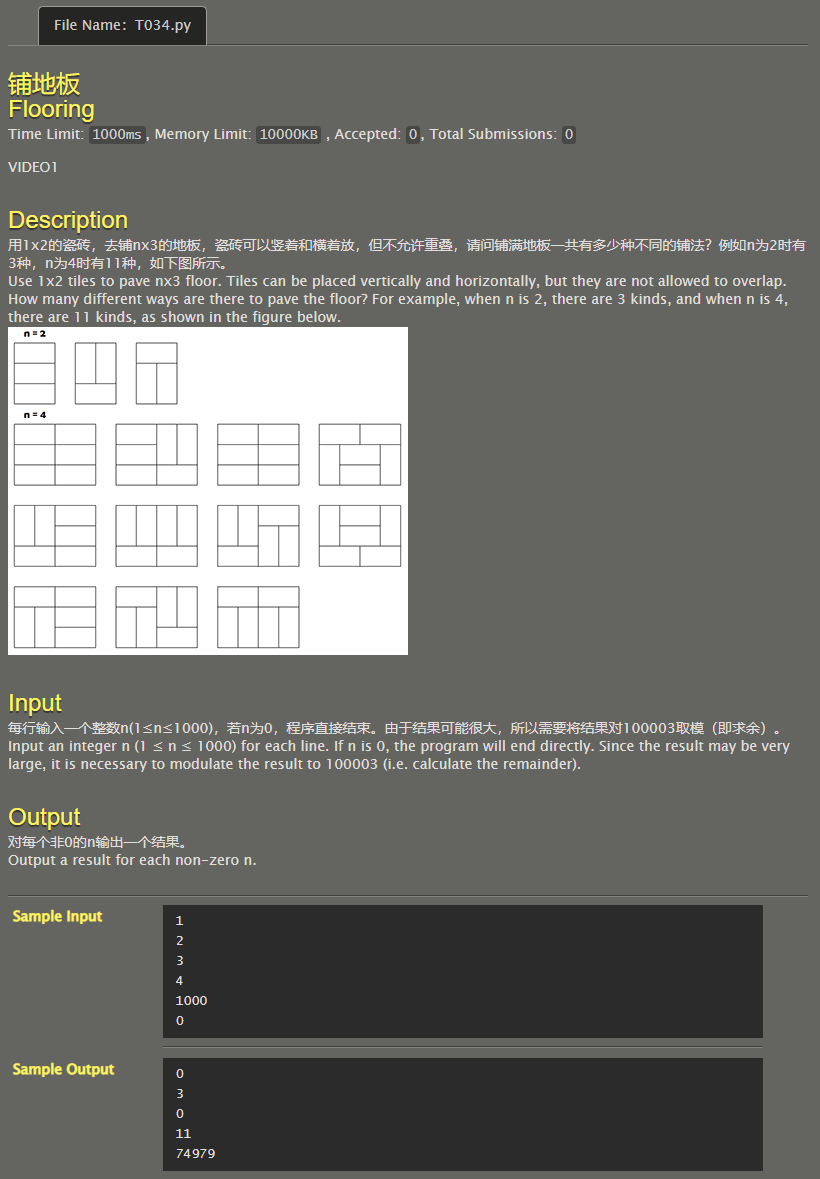
- n if it is an odd number, the number of schemes must be 0, because the last column cannot be spliced
- If n is even, it can be solved recursively

That's it d p [ 4 ] = d p [ 2 ] ∗ 4 = 12 dp[4]=dp[2]*4=12 dp[4]=dp[2] * 4 = 12, which is obviously different from d p [ 4 ] = 11 dp[4]=11 dp[4]=11 is not in conformity, because the situation of full vertical splicing is repeated, and it is calculated once more d p [ i − 4 ] dp[i-4] dp[i − 4], so it's d p [ i ] = d p [ i − 2 ] ∗ 4 − d p [ i − 1 ] ( his in d p [ 0 ] = 1 ) dp[i]=dp[i-2]*4-dp[i-1] (where dp[0]=1) dp[i]=dp[i − 2] * 4 − dp[i − 1] (where dp[0]=1)
Mod=100003
dp=[0 for i in range(10005)]
dp[0],dp[2]=1,3
for i in range(4,10000,2):
dp[i]=(dp[i-2]*4-dp[i-4])%Mod
while 1:
n=int(input())
if(n==0):
break
print(dp[n])
# Code By Phoenix_ZH
Stick equation
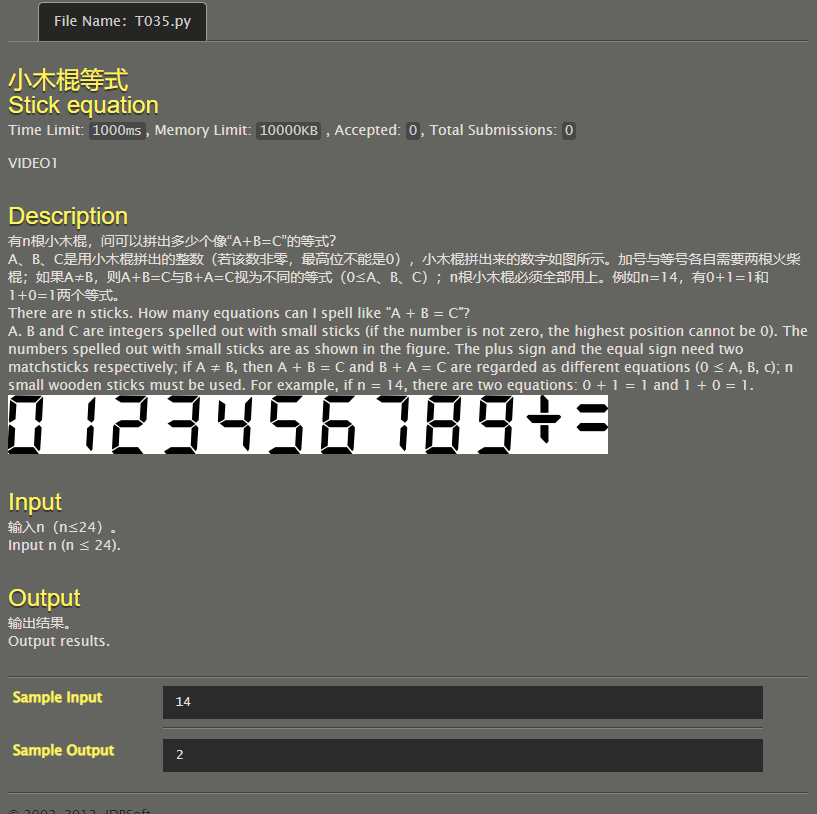
'+' and '=' need 4 wooden sticks. There are only 20 wooden sticks left. You can spell up to 10 numbers and distribute them to the left and right. The answer can have up to 5 digits and the addend can have up to 4 numbers (because you must ensure that an addend is at least 0 or 1, and 1 uses the least wooden sticks). That's the simplest 1111 + 1 = 1112 1111+1=1112 1111 + 1 = 1112 requires 21 sticks. In fact, the situation of 4 digits is impossible, so the addend must be < = 1000. Then directly enumerate the numbers within 1000 to match.
a=[0 for i in range(20)]
a[0],a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9]=6,2,5,5,4,5,6,3,7,6
def cal(x):
if(x==0):
return a[0]
ans=0
while(x):
y=x%10
x//=10
ans+=a[y]
return ans
pass
n=int(input())
ans=0
for i in range(0,1000+1):
for j in range(i,1000+1):
k=i+j
if(cal(i)+cal(j)+4+cal(k)==n):
if(i!=j):
ans+=2
if(i==j):
ans+=1
print(ans)
# Code By Phoenix_ZH
number
There is a problem with the data in this question n < = 100 n<=100 N < = 100, but there is data with n > 100
I thought about one at first O ( n 3 ) O(n^3) O(n3): Enumeration a 1 , a 2 , a 3 a_1,a_2,a_3 a1, a2, a3 , then count the number of schemes, but the submission timed out.
So I made a table: count all the cases of N < = 100:
n = int(input())
print(a[n])
for a in range(0, 100+1):
n=a
ans = 0
for i in range(n+1):
for j in range(n+1):
if((i+j) % 2):
continue
for k in range(n+1):
if((i+j) % 2 == 0 and (j+k) % 3 == 0 and (i+j+k) % 5 == 0):
ans = max(ans, i+j+k)
print("a[%d]=%d"%(a,ans))
Tabulation results:
a=[0 for i in range(100+5)] a[0]=0 a[1]=0 a[2]=5 a[3]=5 a[4]=10 a[5]=10 a[6]=15 a[7]=15 a[8]=20 a[9]=25 a[10]=25 a[11]=30 a[12]=30 a[13]=35 a[14]=40 a[15]=45 a[16]=45 a[17]=50 a[18]=50 a[19]=55 a[20]=55 a[21]=60 a[22]=60 a[23]=65 a[24]=70 a[25]=70 a[26]=75 a[27]=75 a[28]=80 a[29]=85 a[30]=90 a[31]=90 a[32]=95 a[33]=95 a[34]=100 a[35]=100 a[36]=105 a[37]=105 a[38]=110 a[39]=115 a[40]=115 a[41]=120 a[42]=120 a[43]=125 a[44]=130 a[45]=135 a[46]=135 a[47]=140 a[48]=140 a[49]=145 a[50]=145 a[51]=150 a[52]=150 a[53]=155 a[54]=160 a[55]=160 a[56]=165 a[57]=165 a[58]=170 a[59]=175 a[60]=180 a[61]=180 a[62]=185 a[63]=185 a[64]=190 a[65]=190 a[66]=195 a[67]=195 a[68]=200 a[69]=205 a[70]=205 a[71]=210 a[72]=210 a[73]=215 a[74]=220 a[75]=225 a[76]=225 a[77]=230 a[78]=230 a[79]=235 a[80]=235 a[81]=240 a[82]=240 a[83]=245 a[84]=250 a[85]=250 a[86]=255 a[87]=255 a[88]=260 a[89]=265 a[90]=270 a[91]=270 a[92]=275 a[93]=275 a[94]=280 a[95]=280 a[96]=285 a[97]=285 a[98]=290 a[99]=295 a[100]=295
However, the RE is submitted, indicating that n > 100 is likely to be greater than 500, otherwise O ( n 3 ) O(n^3) O(n3) will not time out.
Then I used a wrong way to enumerate it from large to small a 1 , a 2 , a 3 a_1,a_2,a_3 a1, a2, a3, output once the answer is found.
But although this practice is wrong, it is wrong: so greedy n = 99 n=99 When n=99, 285 is output, but in fact, the answer should be 295 (you can check the answer by typing the table).
Since AC is, I'm too lazy to think about it again. If you have O ( n 2 ) or person O ( n l o g n ) O(n^2) or O(nlogn) O(n2) or O(nlogn) please @ me.
n = int(input())
for i in range(n,0,-1):
for j in range(n,0,-1):
if (i+j)%2:
continue
for k in range(n,0,-1):
if((j+k)%3==0 and (i+j+k)%5==0):
print(i+j+k)
exit(0)
Power
Direct fast exponentiation, and then take the module of 10000 in the intermediate process. In fact, you can also take the module of 10. In short, it is enough to keep the single digits.
def qpow(a,b,c):
a,ans=a%c,1
while b!=0:
if b&1:ans=(ans*a)%c
b>>=1
a=(a*a)%c
return ans
pass
while(1):
a,b=map(int,input().split())
if(a==0 and b==0):
break
ans=qpow(a,b,10000)
print(ans%10)
# Code By Phoenix_ZH
Eat candy
set up d p [ i ] dp[i] dp[i] is the number of schemes for eating I sweets.
that d p [ 1 ] = 1 , d p [ 2 ] = 2 , d p [ 3 ] = 3 dp[1]=1,dp[2]=2,dp[3]=3 dp[1]=1,dp[2]=2,dp[3]=3
You can eat one or two candies at a time, so if you eat i candies in total, and you either eat one or two this time, there will be one before i − 1 i-1 i − 1 or i − 2 i-2 i − 2 candies, then the number of schemes is d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] dp[i]=dp[i-1]+dp[i-2] dp[i]=dp[i−1]+dp[i−2]
dp=[0 for i in range(1000+5)]
dp[1],dp[2],dp[3]=1,2,3
for i in range(4,100):
dp[i]=dp[i-1]+dp[i-2]
while(1):
n=int(input())
if (n==0):
break
print(dp[n])
# Code By Phoenix_ZH
Climb the stairs
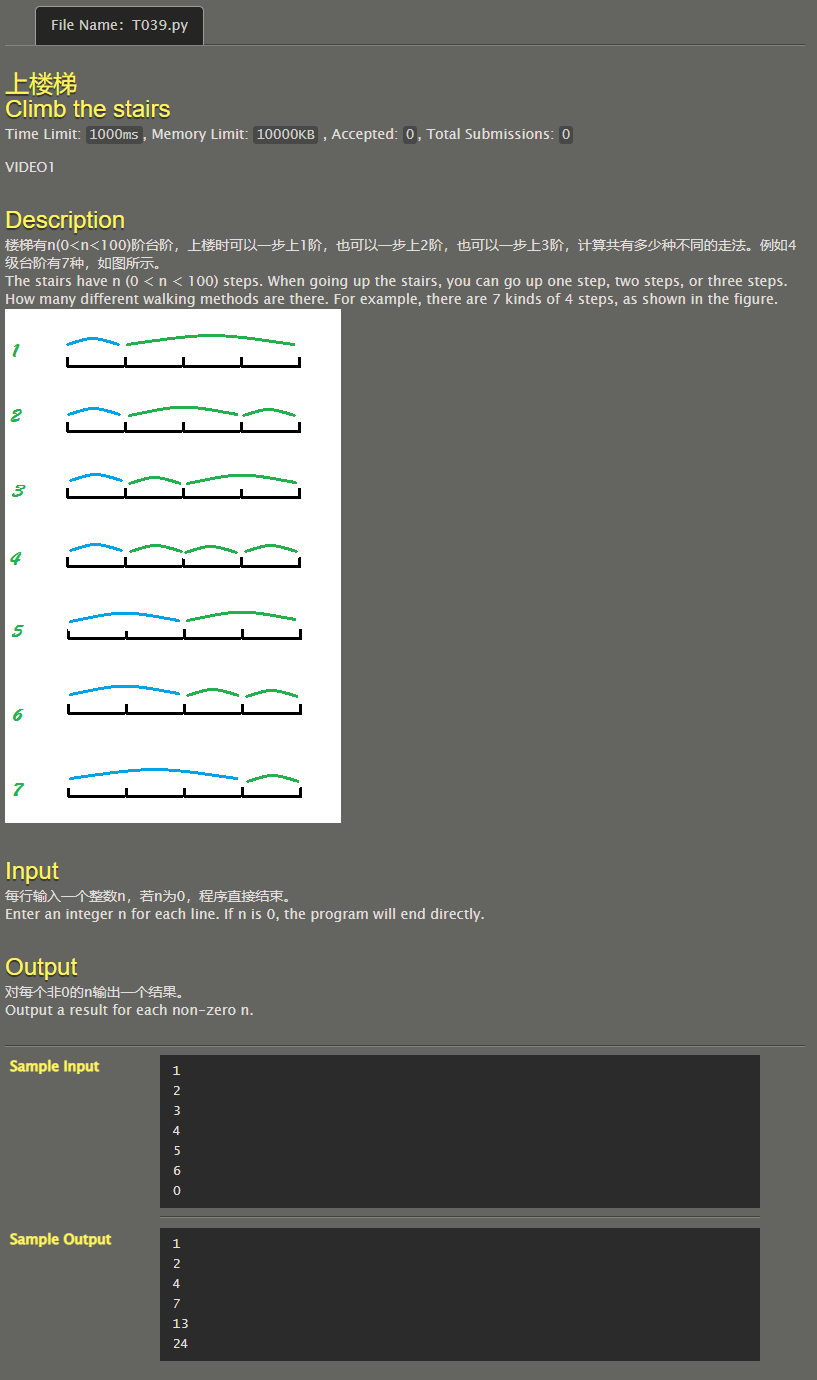
The method is as like as two peas, but the initialization is different, and the transfer equation changes slightly.
dp=[0 for i in range(1000+5)]
dp[1],dp[2],dp[3]=1,2,4
for i in range(4,500+5):
dp[i]=dp[i-1]+dp[i-2]+dp[i-3]
while(1):
n=int(input())
if(n==0):
break
print(dp[n])
Closest score
Direct enumeration can get the maximum score that meets the requirements. Finally, call math.. GCD function obtains the greatest common divisor.
import math
n,a,b=map(int,input().split())
fz,fm=1,n
for i in range(1,n+1):
for j in range(n,0,-1):
if((a*j>b*i)and(fz*j<fm*i)):
fm,fz=j,i
g=math.gcd(fm, fz)
fm,fz=fm//g. FZ / / g # score reduction
print(fz,fm,sep='/')
# Code By Phoenix_ZH