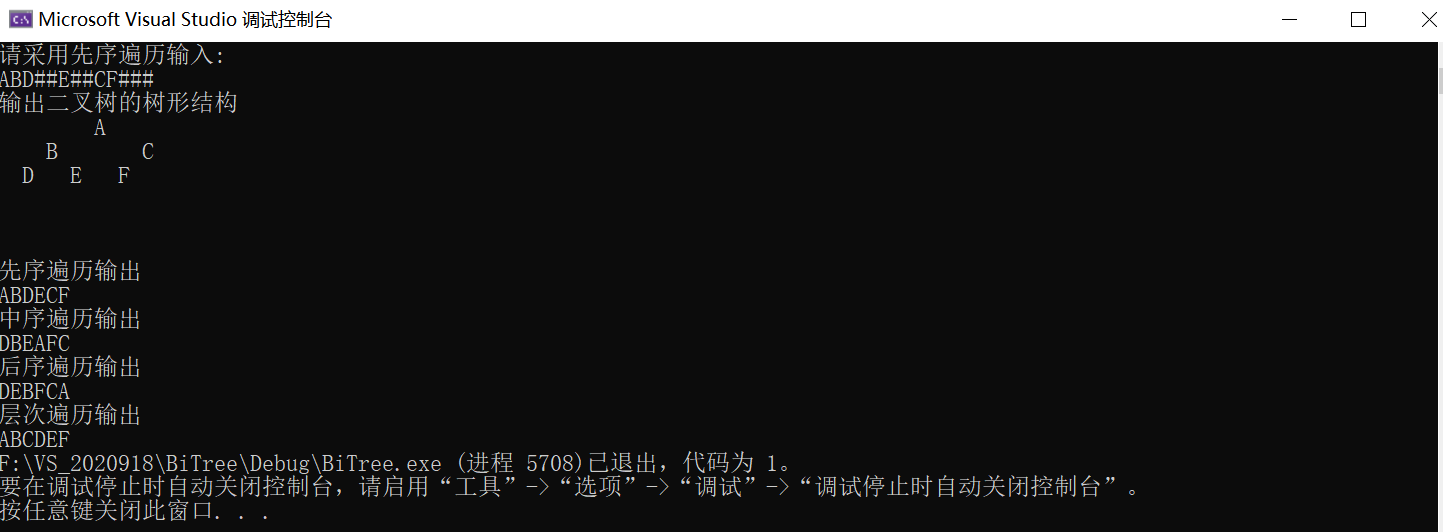
Non recursive traversal algorithm of binary tree

Posted by aleigh on Tue, 19 Oct 2021 02:23:39 +0200

Non recursive traversal algorithm of binary tree

Traversal of binary tree refers to accessing each node of binary tree, and each node is accessed only once. The traversal of binary tree can be divided into four ways according to the composition of binary tree and the order of accessing nodes: first order traversal, middle order traversal, second order traversal and level traversal. Please give the idea and code of at least one non recursive algorithm of traversal mode, and give an example to demonstrate the execution process of the algorithm.

Preorder traversal

Algorithm idea: the stack is used to realize the non recursive algorithm of preorder traversal. Create stack and initialize. Traverse the node, if the node exists, put it on the stack, and output the value of the node, pointing to its left child; Otherwise, access the node and point to its right child. If the node does not exist or the stack is empty, the traversal ends.

code:

//Preorder traversal binary tree
void PreOrder(BiTree T)
{
	SqStack* S;
	S = InitStack();
	BiTreeNode* p;
	p = T;
	while (p|| !StackEmpty(*S))
	{
		if (p)
		{
			printf("%c",p->data);
			Push(S, p);
			p = p->LChild;
		}
		else
		{
			Pop(S, &p);
			p = p->RChild;
		}
	}
}

Demonstrate the process (take the precedence traversal input ABD##E##CF### as an example)

The root node A is stacked and the value of the node is printed, and P points to its left child

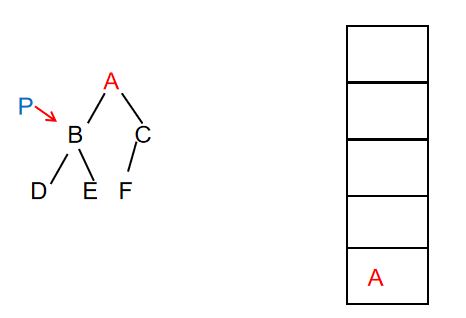
Output: A

Continue to traverse the node. At this time, node B exists and prints the value of the node, then put the node on the stack, and P points to the left child of node B

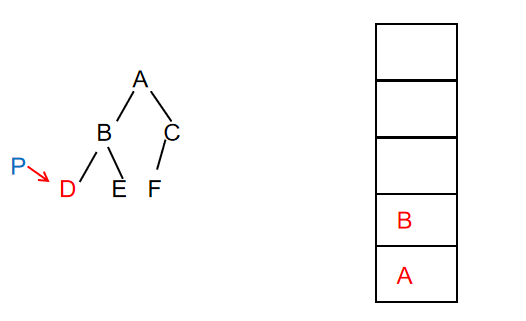
Output: AB

Continue to traverse the node. At this time, node D exists and prints the value of the node, then put the node on the stack, and P points to the left child of node D

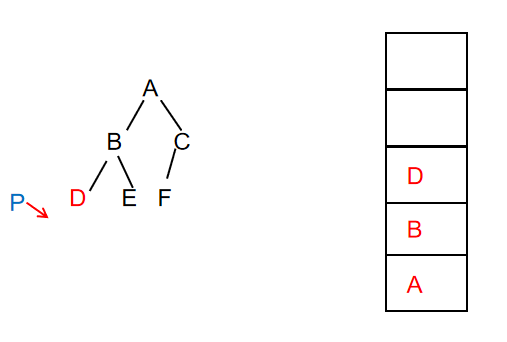
Output: ABD

Continue to traverse the node. At this time, the left child of node D does not exist, then the top element of the stack is out of the stack, and P points to the right child of node D

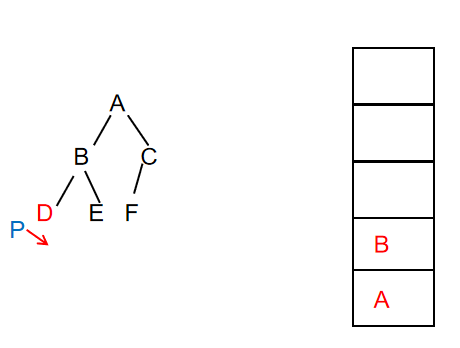
At this time, output: ABD (unchanged)

Continue to traverse the node. At this time, the right child of node D does not exist, then the top element of the stack is out of the stack, and P points to the right child of node B

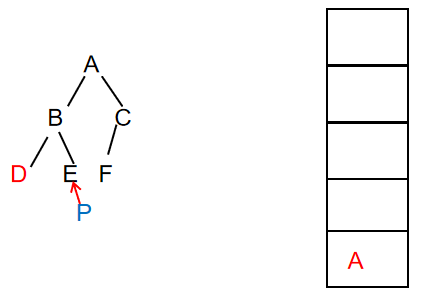
At this time, output: ABD (unchanged)

Continue to traverse the node. At this time, node e exists and prints the value of the node, then put the node on the stack, and P points to the left child of node E

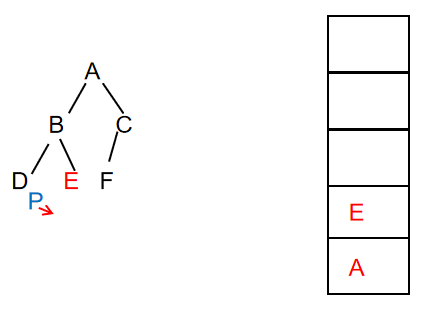
Output: ABDE

Continue to traverse the node. At this time, the left child of node e is empty, then the top element of the stack is out of the stack, and P points to the right child of node E

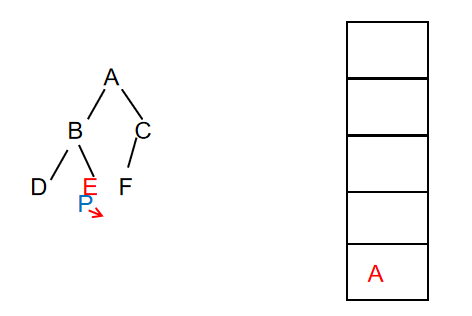
At this time, output: ABDE (unchanged)

Continue to traverse the node. At this time, the right child of node E is empty, then the top element of the stack is out of the stack, and P points to the right child of node A

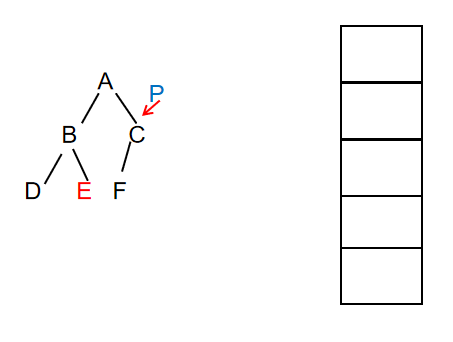
At this time, output: ABDE (unchanged)

Continue to traverse the node. At this time, node C exists and prints the value of the node, then put the node on the stack, and P points to the left child of node C

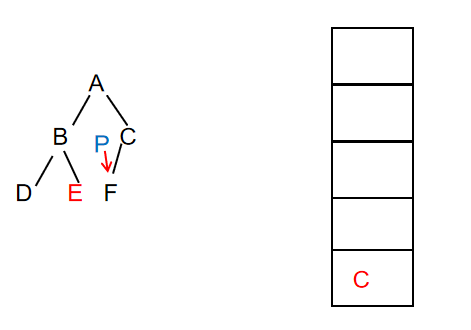
At this time, output: ABDEC

Continue to traverse the node. At this time, node f exists and prints the value of the node, then put the node on the stack, and P points to the left child of node F

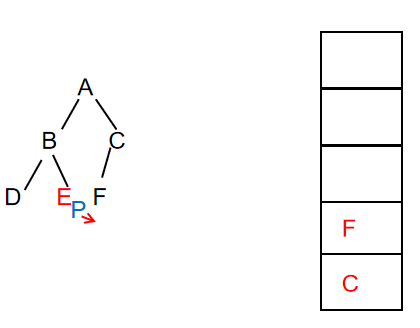
At this time, output: ABDECF

Continue to traverse the node. At this time, the left child of node f is empty, then the stack top element f is out of the stack, and P points to the right child of node F

At this time, the right child of node F is also empty. Continue to take the top element C out of the stack, and P points to the right child of node C. at this time, the node pointed to by P is empty, and the stack is also empty. The traversal ends.

Medium order traversal

Algorithm idea: it also uses stack, which is the same as preorder traversal, but the output is in different positions. Create stack and initialize. Traverse the node. If the node exists, put it on the stack and point to its left child; Otherwise, access the node and output the value of the node, pointing to its right child. If the node does not exist or the stack is empty, the traversal ends

code:

//Middle order traversal binary tree
void InOrder(BiTree T)
{
	SqStack* S;
	S = InitStack();
	BiTreeNode* p;
	p = T;
	while (p || !StackEmpty(*S))
	{
		if (p)
		{
			Push(S, p);
			p = p->LChild;
		}
		else
		{
			Pop(S, &p);
			printf("%c", p->data);
			p = p->RChild;
		}
	}
}

Postorder traversal

Algorithm idea: since the post order traversal is the post order traversal of the left subtree of the root node, the post order traversal of the right subtree of the root node, and finally access the root node, the biggest problem is to judge whether the node ends traversing the left subtree, so the following operations are taken to solve it. Similarly, a stack is also used to initialize the stack and traverse the node. If the node exists, the node enters the stack, and the node flag bit 0 indicates that the node has not been traversed its left subtree, and then points to its right node; If the node does not exist, the left subtree satisfying the node has been traversed into the loop, traversing the right subtree of the node. If not satisfied, exit the loop, then continue to get the child node out of the stack, press it into the stack, point to the right child of the child node, and mark the node as 1.

code:

//Postorder traversal
void Postorder(BiTree T)
{
	SqStack* S;
	S = InitStack();
	BiTreeNode* p;
	p = T;
	char tag[Maxsize] = {'0'};
	while (p || !StackEmpty(*S))
	{
		if (p)
		{
			Push(S, p);
			tag[S->top] = '0';//Flag whether the node traverses the right subtree
			p = p->LChild;
		}
		else
		{
			while (tag[S->top] == '1') {
				Pop(S, &p);
				printf("%c",p->data);
			}
			if (S->top == -1) break;
			Pop(S, &p);
			Push(S, p);
			p = p->RChild;
			tag[S->top] = '1';
		}
		

	}
}

level traversal

Algorithm idea: it is realized by using sequential queue. The root node enters the queue and enters the loop. The element indicated by the team head pointer is out of the queue and the value of its node is output. If the left child of the node exists, the left child enters the queue. If the right child of the node exists, the right child enters the queue until the team head pointer and the team tail pointer are equal and exit the loop.

code:

//level traversal 
void Levelorder(BiTree T)
{
	BiTree Q[Maxsize];
	int front, rear;
	if (T == NULL)return;
	front = -1;
	rear = 0;
	Q[rear] = T;
	while (front != rear)
	{
		front++;
		printf("%c",Q[front]->data);
		if (Q[front]->LChild != NULL)
		{
			rear++;
			Q[rear] = Q[front]->LChild;
		}
		if (Q[front]->RChild != NULL)
		{
			rear++;
			Q[rear] = Q[front]->RChild;
		}
	}
}

Code summary

//Non recursive first order traversal, middle order traversal and second order traversal can be realized by stack
//Hierarchical traversal can be implemented by using queues
//Author: Second to none
#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#include<Windows.h>
#include<math.h>
#define Maxsize 30
typedef char ElemType;
void gotoxy(int x, int y)
{
	COORD c;
	c.X = x - 1;
	c.Y = y - 1;
	SetConsoleCursorPosition(GetStdHandle(STD_OUTPUT_HANDLE), c);
}
typedef struct BiTreeNode
{
	ElemType data;
	struct BiTreeNode* LChild, * RChild;
}*BiTree;
typedef struct SqStack
{
	BiTree data[Maxsize];
	int top;
}*Stack;
//Create stack
Stack InitStack()
{
	Stack S;
	S = (Stack)malloc(sizeof(SqStack));
	S->top = -1;
	return S;
}
//Stack empty
int StackEmpty(SqStack S)
{
	if (S.top == -1)return 1;
	else return 0;
}
//Push 
void Push (Stack S,BiTree p)
{
	S->top++;
	S->data[S->top] = p;
}
//Out of stack
void Pop(Stack S, BiTree* p)
{
	*p = S->data[S->top];
	S->top--;
}
BiTree CreateBiTree()
{
	char ch;
	BiTree T;
	scanf_s("%c",&ch,1);
	if (ch == '#')T = NULL;
	else {
		T = (BiTree)malloc(sizeof(BiTreeNode));
		T->data = ch;
		T->LChild = CreateBiTree();
		T->RChild = CreateBiTree();
	}
	return T;
}
//Preorder traversal binary tree
void PreOrder(BiTree T)
{
	SqStack* S;
	S = InitStack();
	BiTreeNode* p;
	p = T;
	while (p|| !StackEmpty(*S))
	{
		if (p)
		{
			printf("%c",p->data);
			Push(S, p);
			p = p->LChild;
		}
		else
		{
			Pop(S, &p);
			p = p->RChild;
		}
	}
}
//Middle order traversal binary tree
void InOrder(BiTree T)
{
	SqStack* S;
	S = InitStack();
	BiTreeNode* p;
	p = T;
	while (p || !StackEmpty(*S))
	{
		if (p)
		{
			Push(S, p);
			p = p->LChild;
		}
		else
		{
			Pop(S, &p);
			printf("%c", p->data);
			p = p->RChild;
		}
	}
}
//Postorder traversal
void Postorder(BiTree T)
{
	SqStack* S;
	S = InitStack();
	BiTreeNode* p;
	p = T;
	char tag[Maxsize] = {'0'};
	while (p || !StackEmpty(*S))
	{
		if (p)
		{
			Push(S, p);
			tag[S->top] = '0';//Flag whether the node traverses the right subtree
			p = p->LChild;
		}
		else
		{
			while (tag[S->top] == '1') {
				Pop(S, &p);
				printf("%c",p->data);
			}
			if (S->top == -1) break;
			Pop(S, &p);
			Push(S, p);
			p = p->RChild;
			tag[S->top] = '1';
		}
		

	}
}
//level traversal 
void Levelorder(BiTree T)
{
	BiTree Q[Maxsize];
	int front, rear;
	if (T == NULL)return;
	front = -1;
	rear = 0;
	Q[rear] = T;
	while (front != rear)
	{
		front++;
		printf("%c",Q[front]->data);
		if (Q[front]->LChild != NULL)
		{
			rear++;
			Q[rear] = Q[front]->LChild;
		}
		if (Q[front]->RChild != NULL)
		{
			rear++;
			Q[rear] = Q[front]->RChild;
		}
	}
}
int GetHightOfTree(BiTree T)
{
	int rh = 0, lh = 0;
	if (!T)return 0;
	else
	{
		lh = GetHightOfTree(T->LChild);
		rh = GetHightOfTree(T->RChild);
		return(lh > rh ? lh : rh) + 1;
	}
}
void DisplayBinTree(BiTree T, int col, int row, int h)
{
	if (T)
	{
		gotoxy(col, row);
		printf("%c", T->data);
		DisplayBinTree(T->LChild, col - h, row + 1, h / 2);
		DisplayBinTree(T->RChild, col + h, row + 1, h / 2);
	}
}
void DisplayTree(BiTree T)
{
	int k = 0;
	k = GetHightOfTree(T);
	DisplayBinTree(T, (int)pow(2, k - 1) * 2 + 1, 4, (int)pow(2, k - 1));
	printf("\n\n\n");
}
int main()
{
	BiTree T;
	printf("Please traverse the input in sequence:\n");
	T = CreateBiTree();
	printf("Tree structure of output binary tree");
	DisplayTree(T);
	printf("\n Preorder traversal output\n");
	PreOrder(T);
	printf("\n Middle order traversal output\n");
	InOrder(T);
	printf("\n Postorder traversal output\n");
	Postorder(T);
	printf("\n Hierarchical traversal output\n");
	Levelorder(T);
	return 1;
}

Running screenshot

Topics: C Algorithm data structure

Programmer Think

Non recursive traversal algorithm of binary tree

Non recursive traversal algorithm of binary tree

Preorder traversal

Medium order traversal

Postorder traversal

level traversal

Code summary

Running screenshot

Hot Topics