Looking for module order

First,

Transcription factors combine with specific sequences upstream of genes to regulate gene expression, but in different individuals, there will be some differences in this sequence. In this chapter, greedy and random algorithms are used to find this sequence: finding module order.

2, Some concepts:

1. The meaning of score and Profile is shown in the figure

According to the profile matrix, the probability of a kmer under a profile can be calculated

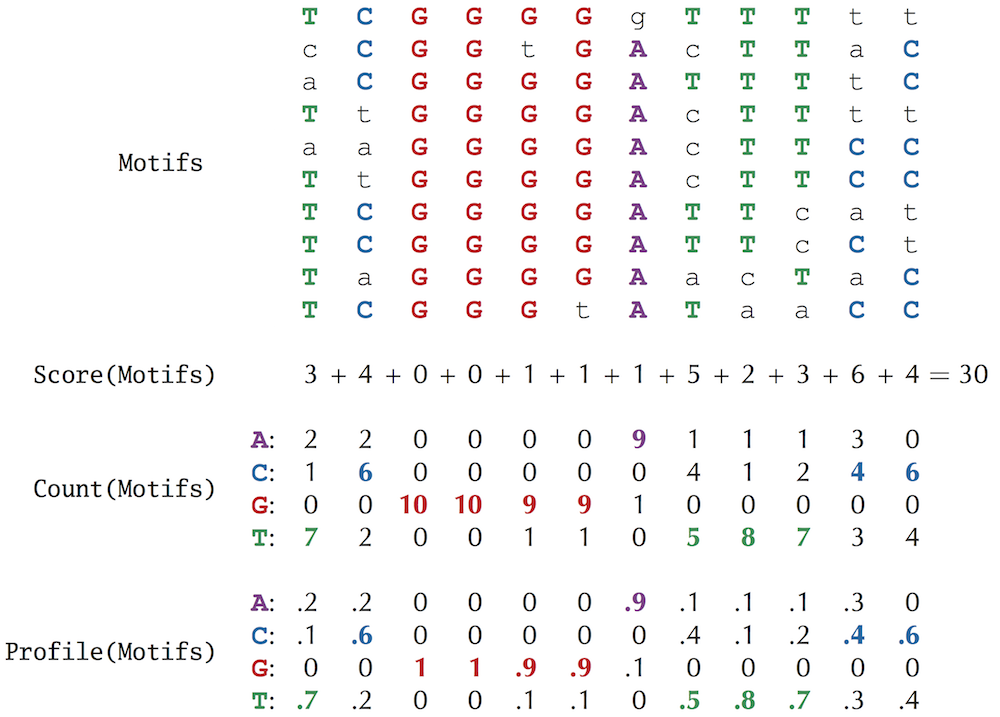
Three.

Ask questions: Motif Finding Problem:

Given a collection of strings, find a set of k-mers, one from each string, that minimizes the score of the resulting motif.

Input: A collection of strings Dna and an integer k.

Output: A collection Motifs of k-mers, one from each string in Dna, minimizing Score(Motifs) among all possible choices of k-mers.

In a set of sequences, look for a set of k-mer s whose Score is the lowest (or the sum of Hamming distance with the consumers sequence is the smallest)

 

1 traversal

MedianString(Dna, k)
        distance ← ∞
        for each k-mer Pattern from AA...AA to TT...TT
            if distance > d(Pattern, Dna)
                 distance ← d(Pattern, Dna)
                 Median ← Pattern
        return Median

 

2 greedy motifsearch

GREEDYMOTIFSEARCH(Dna, k, t)
        BestMotifs ← motif matrix formed by first k-mers in each string
                      from Dna
        for each k-mer Motif in the first string from Dna
            Motif1 ← Motif
            for i = 2 to t
                form Profile from motifs Motif1, ..., Motifi - 1
                Motifi ← Profile-most probable k-mer in the i-th string
                          in Dna
            Motifs ← (Motif1, ..., Motift)
            if Score(Motifs) < Score(BestMotifs)
                BestMotifs ← Motifs
        output BestMotifs

Http://www.mrgraeme.co.uk/green-motif-search/

 

*Greedy motifsearch with pseudocounts

Pseudo amounts: set 0 item to a smaller value when forming profile matrix

GreedyMotifSearch(Dna, k, t)
        form a set of k-mers BestMotifs by selecting 1st k-mers in each string from Dna
        for each k-mer Motif in the first string from Dna
            Motif1 ← Motif
            for i = 2 to t
                apply Laplace's Rule of Succession to form Profile from motifs   Motif1, ..., Motifi-1
                Motifi ← Profile-most probable k-mer in the i-th string in Dna
            Motifs ← (Motif1, ..., Motift)
            if Score(Motifs) < Score(BestMotifs)
                BestMotifs ← Motifs
        output BestMotifs

 

3. Random motif search

RandomizedMotifSearch(Dna, k, t)
　　　　　#Randomly take k-mer from each DNA and generate a set of motifs
        randomly select k-mers Motifs = (Motif1, ..., Motift) in each string from Dna
        BestMotifs ← Motifs
        while forever
            Profile ← Profile(Motifs)#Forming Profile matrix according to motifs
            Motifs ← Motifs(Profile, Dna) #Generate a set of motifs with the greatest probability from a set of DNA according to the profile matrix
            if Score(Motifs) < Score(BestMotifs)
                BestMotifs ← Motifs
            else
                return BestMotifs

The reason why random algorithm works is that a group of randomly selected Motifs may select a potentially correct k-mer, and then form a tilt in this until a better solution is found

Improvement: in the previous algorithm, each iteration generates a new set of Motifs randomly, which may discard the potential correct module order. The improved method is to change only one row of k-mer at a time

GibbsSampler(Dna, k, t, N)
        randomly select k-mers Motifs = (Motif1, ..., Motift) in each string from Dna
        BestMotifs ← Motifs
        for j ← 1 to N
            i ← Random(t)
            Profile ← profile matrix constructed from all strings in Motifs except for Motif[i]
            Motif[i] ← Profile-randomly generated k-mer in the i-th sequence
            if Score(Motifs) < Score(BestMotifs)
                BestMotifs ← Motifs
        return BestMotifs