1, Representation of data

1. Binary conversion

Click jump to explain the hexadecimal conversion

For example:

 Different letters are added after numbers to represent different carry systems.
B(Binary)Represents binary,
O(Octal)Represents octal,
D(Decimal)Or no decimal,
H(Hexadecimal)Represents hexadecimal.

For example:
take(101011)B Convert to octal, divide numbers from right to left, and every 3 digits can correspond to an octal digit
 Then 101011 is divided into 101 and 011, and 101= 5，011=3
 therefore(101011)B=(53)O

take(101011)B Convert to decimal,
Equal to 1×2^5+1×2^3+1×2^1+1×2^0 = 43
 therefore(101011)B=(43)D

take(101011)B Convert to hexadecimal, divide numbers from right to left, and every four digits can correspond to one hexadecimal digit
 Then 101011 is divided into 10 and 1011, and the completion of 10 is 0010 and 1011
 And 0010=1×2^1= 2，1011=1×2^3+1×2^1+1×2^0 = 11 = B
 therefore(101011)B==(2B)H

R-ary to decimal uses "weighted expansion"

For example: binary to decimal:

10100.01 = 1×2^4+1×2^2+1×2^-2

For example: convert from hex to decimal:

604.01 = 6×7^2+4×7^0+1×7^-2

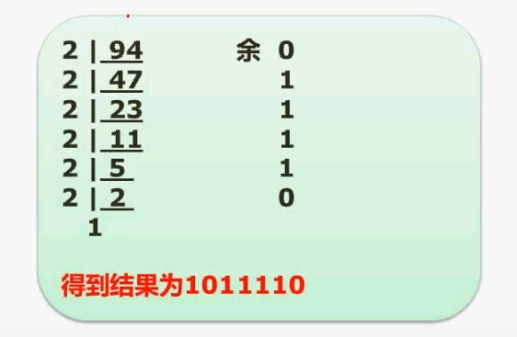
Decimal to R use "short division"

For example: convert decimal number 94 to binary:

For example: conversion between binary and octal and hexadecimal:

Binary to octal (every three digits from right to left can correspond to one octal digit)

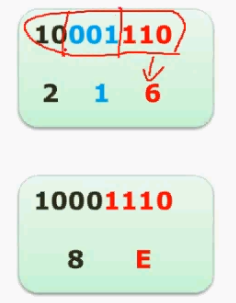
Binary to hexadecimal (every four digits from right to left can correspond to one hexadecimal digit)

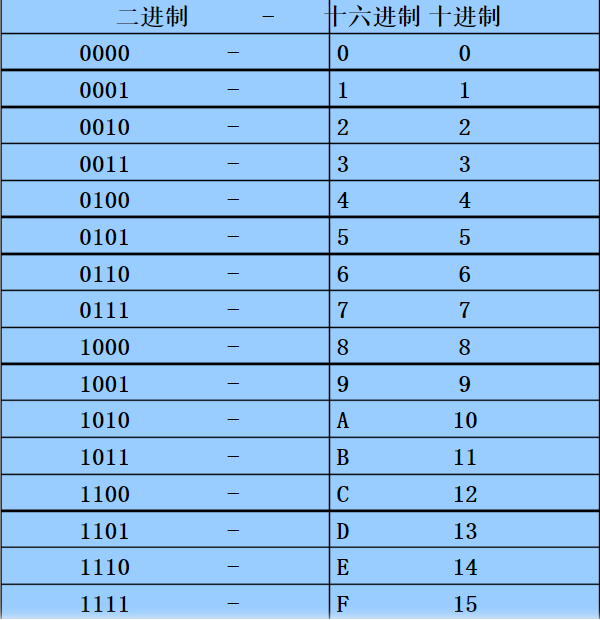
In hex:

• 10 -- represented by A
• 11 -- represented by B
• 12 -- represented by C
• 13 - represented by D
• 14 - denoted by E
• 15 - denoted by F
• 16 - denoted by G

2. Source code, complement and inverse code

Click to view: Exploration of source code, complement and inverse code

3. Floating point operation

For example:

1000-→1.0×10^3
119-→1.19×10^2
 Adding two numbers:
First, the order (convert the lower order to the higher order to ensure the same order)——→Then calculate the mantissa——→Finally, format the results
1.19×10^2 Convert to 0.119×10^3-→1.0+0.119=1.119-→Add result 1.119×10^3 Format is still×10^3(Mantissa cannot be 0 or more than 1 digits)

be careful:
The formatted result cannot be 0.1119×10^4 Or 11.19×10^2</font>

4. Composition of arithmetic unit and controller

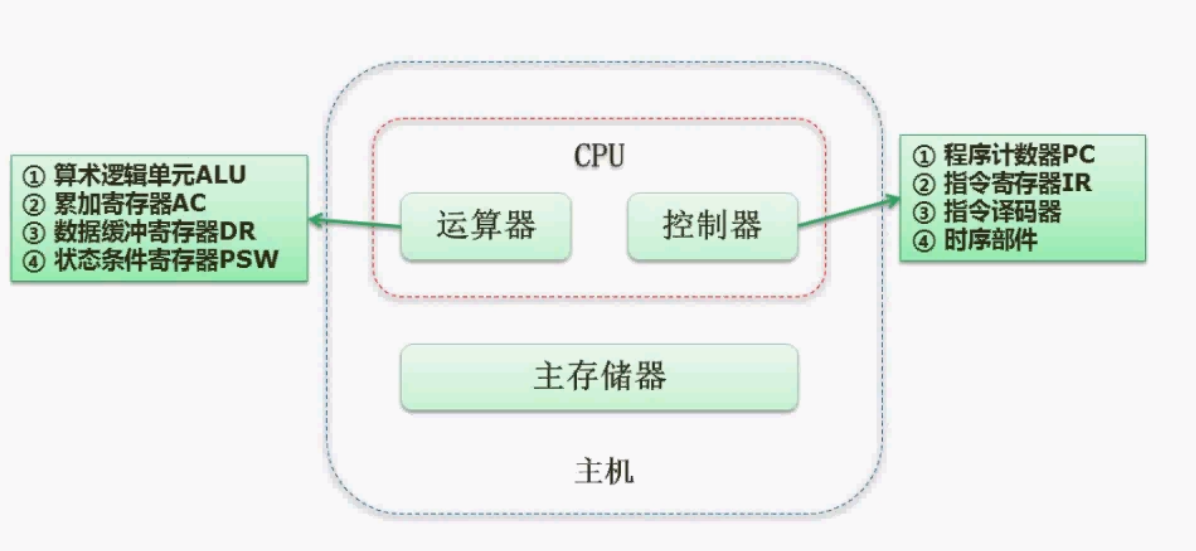
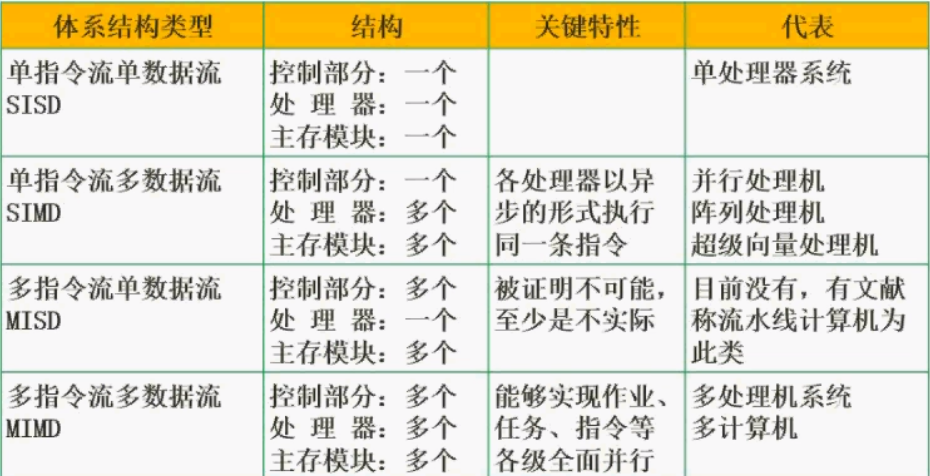
2, Classification of computer architecture Flynn

3, Comparison of CISC and RISC instruction types

4, Assembly line

Pipeline concept

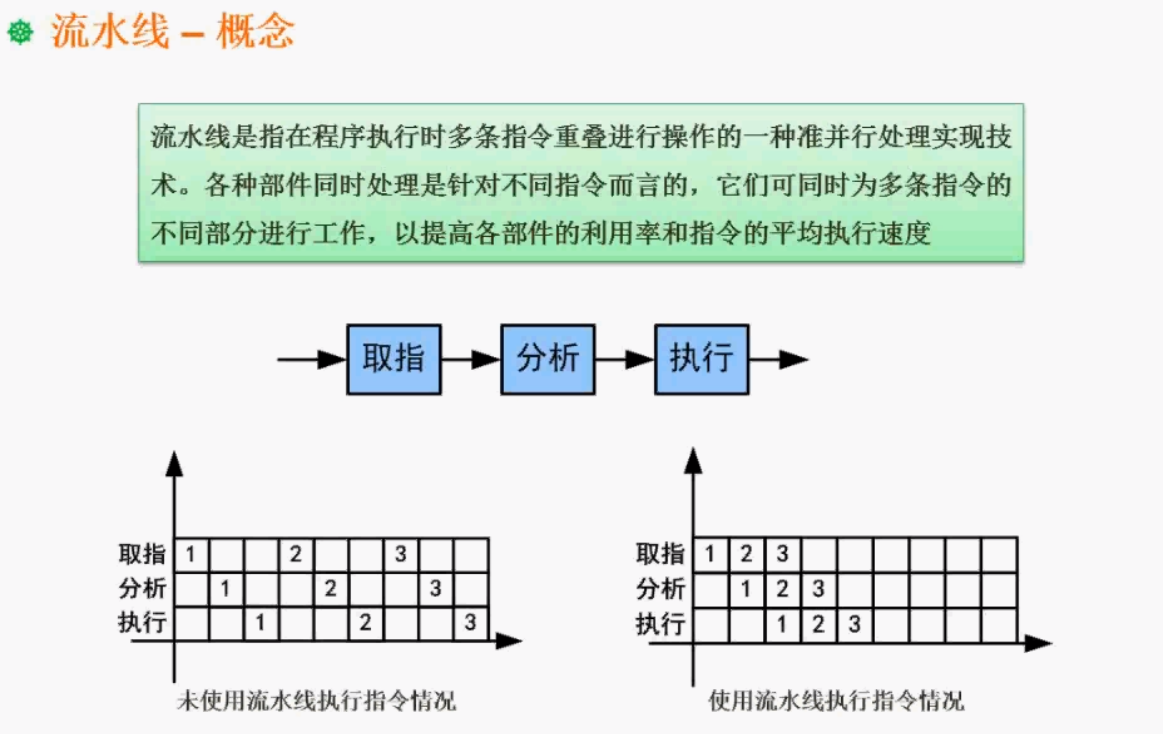
1. Pipeline calculation

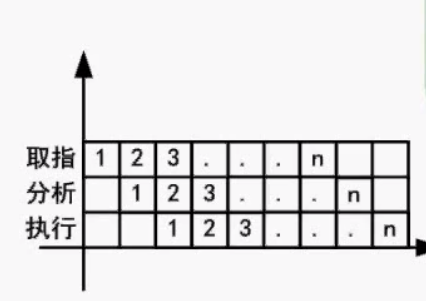
For example, as shown in the figure above, if the instruction pipeline divides an instruction into three parts: fetch, analyze and execute, and the time of the three parts is 2ns for fetch, 2ns for analysis and 1ns for execution respectively. So, what is the pipeline cycle? How long does it take to complete the execution of 100 instructions?

• The pipeline cycle takes the longest execution time: therefore, the pipeline cycle is 2ns,
• The time required to complete the execution of 100 instructions is:

There are two pipeline calculation methods:

(1)Theoretical formula: an execution instruction+(Number of instructions-1)×pipeline cycle 
    (t1+t2+..+tk)+(n-1)×△t Namely:(2+2+1)+(100-1)×2 =203

(2)Practical formula: completion time of a complete task +(Number of instructions-1)×pipeline cycle 
    Here, the time of each part is refined, taking 2 ns
    k+(n-1)×△t Namely: 6+(100-1)×2 =204

2. Throughput calculation of pipeline

For example, what is the pipeline throughput of the above problem?

Pipeline throughput = Number of instructions / Pipeline execution time 
Namely: TP=100 / 203 = 0.493

3. Pipeline speedup

For example, what is the pipeline acceleration ratio of the above problem?

Pipeline speedup ratio  = Pipeline execution time is not used / Use pipeline execution time

Calculate the time it takes to execute 100 instructions without pipelining T = (2+2+1)×100 =500，The pipeline execution time is 203
 so S = 500 / 203 =0.985

The ratio determines the efficiency of the pipeline (that is, the higher the ratio, the higher the pipeline efficiency)

4. Pipeline efficiency

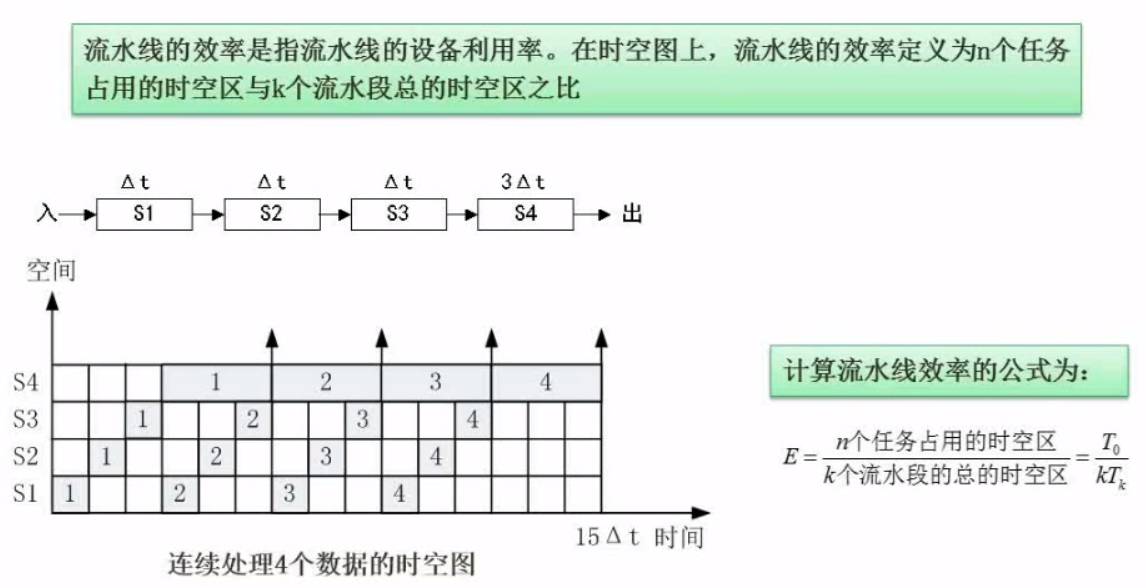
For example, calculate the pipeline efficiency in the figure above?

E = n Space time area occupied by tasks/ K Total space-time area of a pipeline
 Namely: E = (△t +△t +△t +3△t )×4 / 15△t×4

It is equivalent to calculating the ratio of shadow area to total area

5, Computer composition and architecture

Hierarchical storage structure

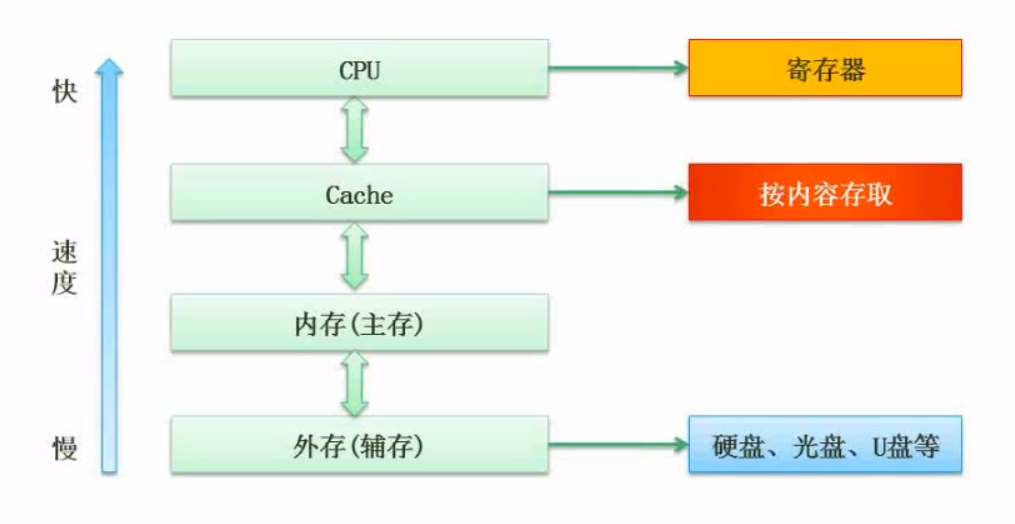
The capacity of the register is very small, but the speed is very fast, so it belongs to the highest level of the storage structure
Cache Cache memory
 Memory
 External storage

The speed gradually slows down from top to bottom, and the memory gradually increases from top to bottom (actually based on the consideration of cost performance)

1. Concept of Cache

For example, the access hit rate of the Cache is 95%, the cycle time of the Cache is 1ns, and the cycle time of the main memory is 1ms. Calculate the average cycle of the system?
Average system cycle = access hit rate × Cache cycle time + (1-access hit rate) × Main memory cycle

2. Locality principle

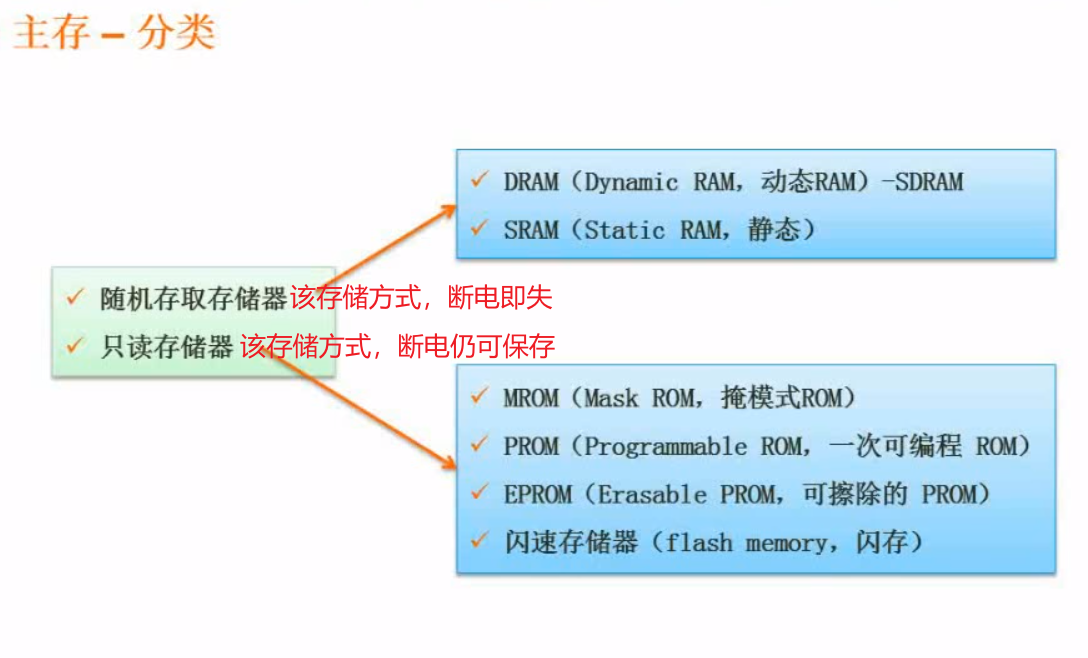
3. Main memory classification

4. Main memory addressing calculation

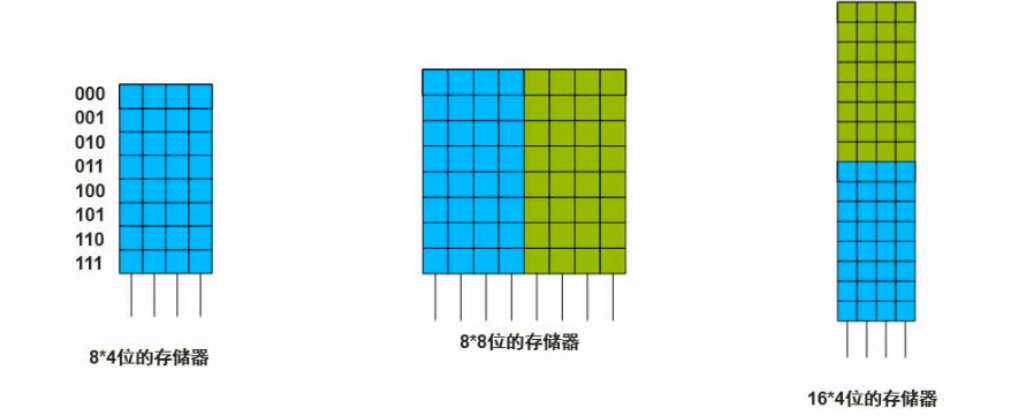
Conversion:
1KB (Kilobyte Kilobyte) = 1024B = 2^10B
1MB (Megabyte Megabytes are referred to as "megabytes") = 1024KB = 2^10KB
1GB (Gigabyte Gigabyte, also known as "Gigabyte") = 1024MB = 2^10MB

In memory:
1KB = 1024B = 1024 byte = 2^10 byte
1MB= 1024KB = 1048576 byte = 2^20 byte
1GB= 1024MB = 1073741824 byte = 2^30 byte
1TB= 1024GB = 1099511627776 byte = 2^40 byte
1PB= 1024TB = 1125899906842624 byte = 2^50 byte

Exercise 1

Solution: byte conversion: 1 MB=2^20B，Therefore 16 MB=2^24B,
             1B(Bytes)=8bit，So 16 MB=2^24×8bit，
And address by byte, that is, every 8 bit Make an address,So you need 2^24×8bit/8bit=2^24 An address.
Therefore, to generate so many addresses, the main memory address needs to be represented by at least 24 binary numbers.

If the above question is changed to use 4 as the address, how many bits does the main memory address need?

Solution: byte conversion: 16 MB=2^24×8bit，2^24×8bit/4bit=2^25 An address.
Therefore, to generate so many addresses, the main memory address needs to be represented by at least 25 binary numbers.

If you change to word addressing and the computer is 64 bits, how many bits does the main memory address need?

Solution: byte conversion: 64 bit=8B，16MB=2^24B，2^24B/8B=2^21 Addresses
 Therefore, to generate so many addresses, the main memory address needs to be represented by at least 21 binary numbers.

Exercise 2

Memory is addressed by bytes. The address ranges from DFFFF to A0000. How many bytes are there in total?

Click jump, hexadecimal addition and subtraction

Solution: calculate memory capacity DFFFF-A0000= 3FFFF
3FFFFH In binary, it is 0011 1111 1111 1111 1111. The 18th bit from right to left is the last 1, that is, the 18th power of 2
 I.e. 2^10×2^8=1KB*256，256 KB;

Exercise 3

For example, if the computer address range C000H is equal to 48k, the calculation method is:

Calculate the following questions:

Solution:
First, hexadecimal calculation: tail address-First address+1，Namely C7FFFH-AC000H+1 = 1C000
 Then convert to decimal:
1C000 = 0001 1100 0000 0000 0000 =2^16+2^15+2^14 B= 2^14(2^2+2^1+1)B =7×2^4×2^10B
 Last byte conversion: B And KB Conversion between:
7×2^4×2^10B/2^10 = 112KB，Therefore, there are 112 K Address units

Storage unit:
112×16/28×16×Y，Namely Y=4，Therefore, each memory cell of the chip stores 4 bits

5. Disk structure and parameters

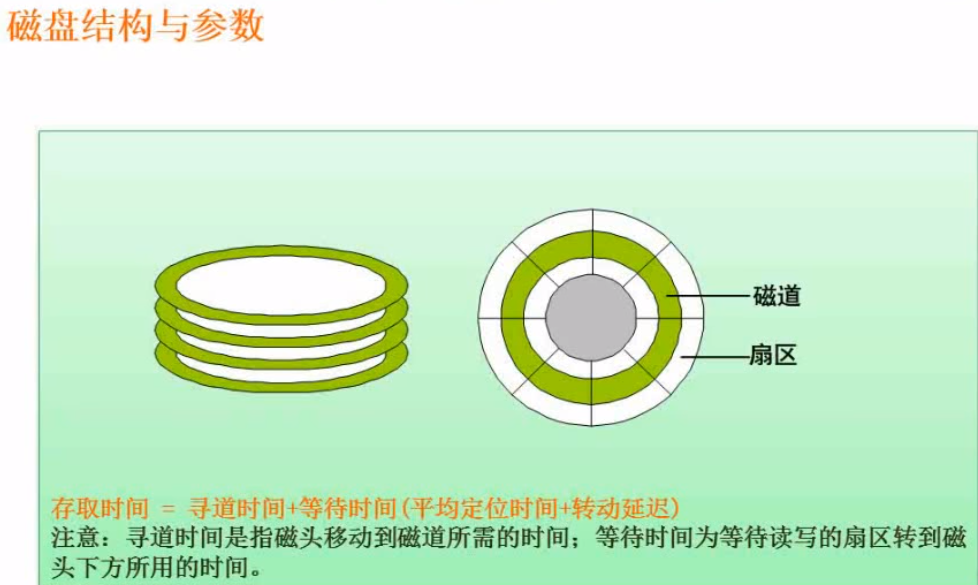
Exercise 1

According to the picture analysis:

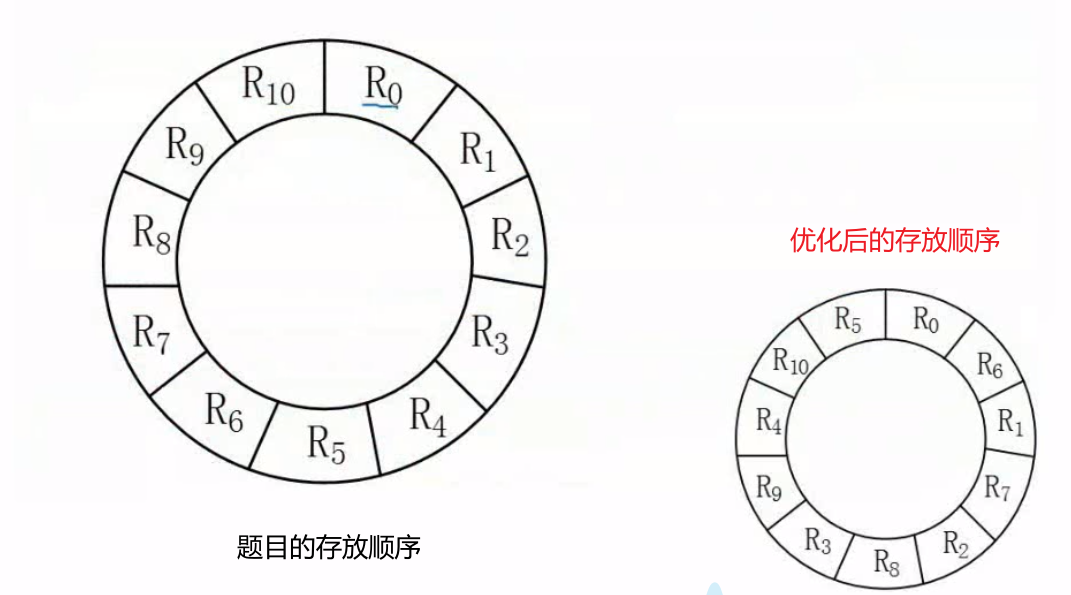
Solution: the disk rotation cycle is 33 ms,It indicates that the disk rotates for one cycle and passes through 11 physical blocks, and the time is 33 ms，The read time for each physical block is 3 ms
 The processing time of each record is also 3 ms,It is a single buffer and can only process a single physical block at a time
 Therefore: R0 The processing time is 3+3=6ms
 Processing time per physical block=The disk rotates for one revolution+processing time 
Therefore: R1 reach R9 It took time to finish processing,(33+3)×10 =360ms
 Total processing time 360+6 = 366ms,Therefore, the answer to question 48 is optional C

The time required for each physical block after distribution optimization is = Read time + processing time 
I.e. (3)+3)×11 = 66ms,Therefore, the answer to question 48 is optional B

6. Bus

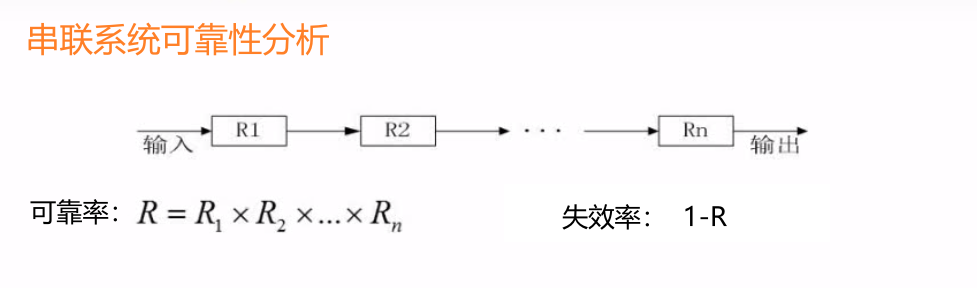
7. System reliability analysis

series system

parallel system

hybrid system

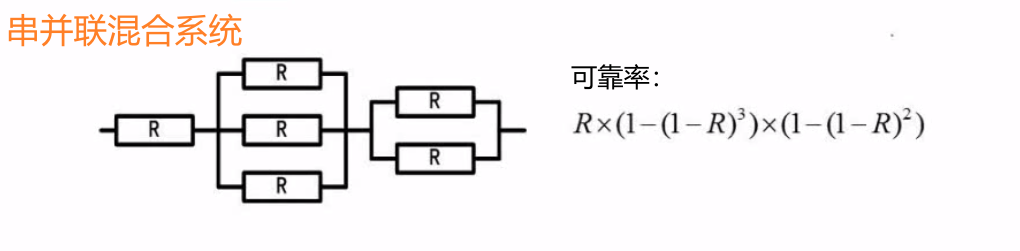
8. Error control

Code distance

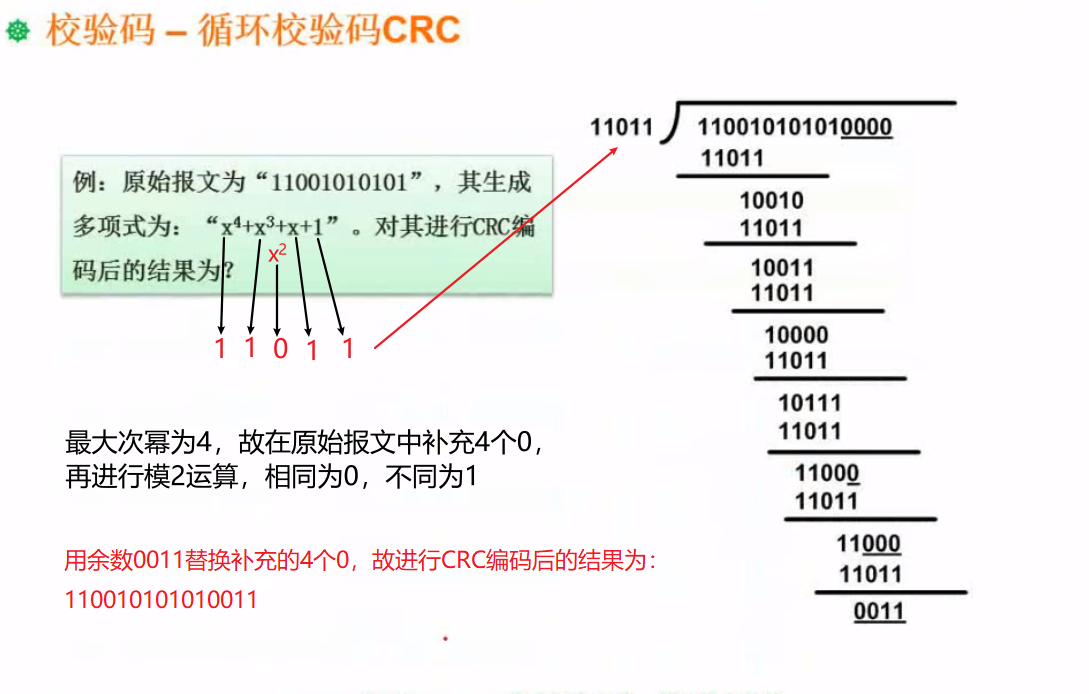
Cyclic check code CRC

Specific case calculation:

Hamming check code