Mind map
remarks:
- Most of the questions and solutions of the sword finger Offer are the crystallization of the leaders in the solution area. They are only used for personal learning

Positive sequence Edition
03 duplicate number in array
Title: find duplicate numbers in the array.
All numbers in an array num of length n are in the range of 0 ~ n-1. Some numbers in the array are repeated, but I don't know how many numbers are repeated, or how many times each number is repeated. Please find any duplicate number in the array.
Example 1:
Input: [2, 3, 1, 0, 2, 5, 3] Output: 2 or 3
analysis:
- Method 1: HashMap or HashSet is OK
- Method 2: the condition gives the array length N and the element range 0 to n-1. Obviously, we want to use the subscript to correspond to the element value
- The number is repeated. It's easy to think of index = = num [index]. It must not be returned for the first time
- When index= nums[index]
- The second time you encounter num [index] = = num [num [index]], this element is repeated and returned directly
- Otherwise, it is neither unrepeated nor subscript corresponding, that is, other elements that are not sorted and out of order. Exchange the elements on num [index] and index to make them return
- Note: for the swap here, it is recommended to rewrite a swap function instead of exchanging in the original function, because the element corresponding to the pointer will lead to a loop
public class Solution {
// Method 1: hash table
public int findRepeatNumber1(int[] nums) {
Set<Integer> set = new HashSet<>();
for (int num : nums) {
if (set.contains(num)) {
return num;
} else {
set.add(num);
}
}
throw new RuntimeException("Nums have not repeat num");
}
// Method 2: array subscript and element correspondence method
public int findRepeatNumber2(int[] nums) {
int index = 0;
while (index < nums.length) {
// 1. Traverse pointer movement conditions: the first index corresponds to the current element, and move the pointer backward. Because it is the first time, it is placed in the front
if (nums[index] == index) {
index++;
continue;
}
// 2. Compare the element values of the current element and its corresponding subscript
if (nums[index] == nums[nums[index]]) {
return nums[index];
} else {
// Homing
swap(nums, index, nums[index]);
}
}
throw new RuntimeException("Nums have not repeat num");
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
04 2D array lookup
Title: in an n * m two-dimensional array, each row is sorted in ascending order from left to right, and each column is sorted in ascending order from top to bottom. Please complete an efficient function, enter such a two-dimensional array and an integer, and judge whether the array contains the integer.
Example:
Existing matrix matrix As follows: [ [1, 4, 7, 11, 15], [2, 5, 8, 12, 19], [3, 6, 9, 16, 22], [10, 13, 14, 17, 24], [18, 21, 23, 26, 30] ]
Analysis: double pointer
- Because the row and column values of two-dimensional arrays are increasing, dichotomy is preferred
- Double pointer problem: start binary search with the lower left coordinate [matrix.len-1][0]
- Less than, column + 1
- Greater than, line - 1
- Equal to, everyone is happy and returns true directly
public class Solution {
// Bottom left coordinate: [matrix.length-1][0]
public boolean findNumberIn2DArray(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0) {
return false;
}
int row = matrix.length - 1;
int col = 0;
while (row >= 0 && col <= matrix[0].length - 1) {
if (matrix[row][col] < target) {
row--;
} else if (matrix[row][col] > target) {
col++;
} else {
return true;
}
}
return false;
}
}
05 replace spaces
Title: please implement a function to replace each space in the string s with "% 20".
Example 1:
Input: s = "We are happy." Output:"We%20are%20happy."
analysis:
-
Because the string needs to be changed, it is convenient for a single thread to use StringBuilder to append()
-
String locator character: s.charAt(i)
- Match and change
public class Solution {
// Traversal of string
public String replaceSpace(String s) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == ' ') {
sb.append("%20");
}else {
sb.append(c);
}
}
return sb.toString();
}
}
06 print linked list from end to end
Title: enter the head node of a linked list and return the value of each node from tail to head (returned by array).
Example 1:
Input: head = [1,3,2] Output:[2,3,1]
analysis:
- Auxiliary stack:
- Traverse the linked list and record the node value with the stack
- Traverse the stack, record the value of the top of the stack with an array, and the top elements are out of the stack at one time
- Recursive method: first understand the auxiliary stack method and realize the first in first out idea of the essence of recursion
- The first time we recurse, we don't record the value because we print from tail to head
- The second time of recursion, record the node value and put it into a List
- Traverse the res array of List size and put the values into res in turn
public class Solution {
// Method 1: auxiliary stack
public int[] reversePrint(ListNode head) {
// LinkedList inherits the queue and stack. You can use the push of the stack and the API of pop
LinkedList<Integer> stack = new LinkedList<>();
while (head != null) {
stack.push(head.val);
head = head.next;
}
int[] res = new int[stack.size()];
for (int i = 0; i < res.length; i++) {
res[i] = stack.pop();
}
return res;
}
// Method 2: recursive method. First understand the auxiliary stack method and realize the first in first out idea of the essence of recursion
public int[] reversePrint1(ListNode head) {
// Store values after recursive reverse order
List<Integer> temp = new ArrayList<>();
// Recursion: in essence, it is a stack of first in and last out. val in reverse order is stored in temp
reverse(head, temp);
// Traverse val in the List into an array of return values
int[] res = new int[temp.size()];
for (int i = 0; i < temp.size(); i++) {
res[i] = temp.get(i);
}
return res;
}
private void reverse(ListNode node, List<Integer> temp) {
if (node == null) {
return;
}
reverse(node.next, temp);
// At the end of recursion of the next layer, accept the node of this layer val
temp.add(node.val);
}
}
07 rebuild binary tree
Title: enter the results of preorder traversal and inorder traversal of a binary tree, please rebuild the binary tree. It is assumed that the input pre order traversal and middle order traversal results do not contain duplicate numbers.
example:
Preorder traversal preorder = [3,9,20,15,7] Medium order traversal inorder = [9,3,15,20,7]
return:
3
/ \
9 20
/ \
15 7
Analysis: learning recursion
- Initialization: root=0 is the index of the preceding traversal root node, left=0 is the left boundary of the left subtree in the middle order, right = the length of the middle order - 1 is the right boundary of the right subtree in the middle order
- Determine the index range of the left and right subtrees and the root node index of the left and right subtrees
- According to the value of root in preOder, go to inOrder to push out the index i of the value
- Left subtree boundary range: [left,i-1]. Left subtree root node root+1
- The root node of the left subtree is obviously the next root in the preorder traversal
- Right subtree boundary range: [i+1,right]. Right subtree root node root+i-left+1
- It is not easy to think of the root node of the right subtree. Associating with the known node range of the left subtree, we can deduce the length of the left subtree, so the length of the left subtree + root index + 1 is the root node index of the right subtree
- Establish recursion
- End condition: right = left > right, which means that no node exists and the recursion ends
- Node is the root node that i currently points to. Every time i recursion returns node as the left and right subtrees of the previous layer
public class Solution {
private int[] preOrder;
private HashMap<Integer, Integer> inOrderMap = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
this.preOrder = preorder;
// The index traversed in the map storage order is convenient for preOrder[root] to return to inorder for searching
for (int i = 0; i < inorder.length; i++) {
inOrderMap.put(inorder[i], i);
}
// Start recursion
return recur(0, 0, inorder.length - 1);
}
private TreeNode recur(int root, int left, int right) {
// Recursive end: end without node value
if (left > right) {
return null;
}
// Establish the root node of the current layer: node
TreeNode node = new TreeNode(preOrder[root]);
// Index value of node in middle order
int i = inOrderMap.get(preOrder[root]);
// Left subtree recursion of node: left subtree root node root+1, left subtree range [left,i-1]
node.left = recur(root + 1, left, i - 1);
// Right subtree recursion of node: right subtree root node root+i-left+1, right subtree range [i+1,right]
node.right = recur(root + i - left + 1, i + 1, right);
// Recursive backtracking: the current node is used as the left or right node of the upper layer
return node;
}
}
09 two stacks implement queue
Title: implement a queue with two stacks. The declaration of the queue is as follows. Please implement its two functions appendTail and deleteHead to insert integers at the end of the queue and delete integers at the head of the queue respectively. (if there are no elements in the queue, the deleteHead operation returns - 1)
Example 1:
Input:["CQueue","appendTail","deleteHead","deleteHead"][[],[3],[],[]]Output:[null,null,3,-1]
Example 2:
Input:["CQueue","deleteHead","appendTail","appendTail","deleteHead","deleteHead"][[],[],[5],[2],[],[]]Output:[null,-1,null,null,5,2]
Tips:
1 <= values <= 10000 At most appendTail,deleteHead 10000 calls
analysis:
- Define a step of pushing push stack into pop stack (amortization time complexity), which meets two principles
- The pop stack is empty. Enough data must be pushed into the pop stack
- Once you want to push data into the pop stack, all the data in the push stack must be pushed in
public class CQueue { private LinkedList<Integer> pushStack; private LinkedList<Integer> popStack; public CQueue() { pushStack = new LinkedList<>(); popStack = new LinkedList<>(); } public void appendTail(int value) { // Add: push first and then pour into popstack push(value); pushToPop(pushStack, popStack); } Public int deletehead() {/ / judge whether the two stacks are empty before leaving the queue if (popstack. Isempty() & & pushstack. Isempty()) {return - 1;}// Delete: pour first, and then delete pushtopop (pushstack, popstack); return popStack. pop(); } // Push stack only pushes in and pop stack only pushes out private void pushtopop (LinkedList < integer > pushstack, LinkedList < integer > popstack) {/ / only when the pop stack is empty, can data be imported from the push stack into the pop stack if (popstack. Isempty()) {while (! Pushstack. Isempty()) {popstack. Push (pushstack. Pop());}}}}
10-I Fibonacci sequence
Title: write a function, enter n, and find the nth term of Fibonacci sequence (i.e. F(N)). Fibonacci sequence is defined as follows:
F(0) = 0, F(1) = 1F(N) = F(N - 1) + F(N - 2), among N > 1.The Fibonacci sequence starts with 0 and 1, and the subsequent Fibonacci numbers are obtained by adding the previous two numbers. The answer needs to take module 1 e9+7(1000000007),If the initial calculation result is 100000008, please return 1.
Example 1:
Input: n = 2 Output: 1
Example 2:
Input: n = 5 Output: 5
Fen Xu: remember to take the model for this problem!
- Recursive method, hand on the line, the interview time timeout can not be used
- Iterative method
- Dynamic programming method
public class Solution { // Method 1: iterative method public int fib1 (int n) {if (n < 2) {return n;} int a = 0; int b = 1; int sum = 0; // N = 0 and n=1, return 0 and 1 directly / / N = 2, go to step 1; n=3, take 2 steps When n=n, take n-1 steps for (int i = 0; I < n - 1; I + +) {sum = (a + b)% 100000007; a = B; b = sum;} return sum; } // Method 2: dynamic programming public int fib2 (int n) {if (n < 2) {return n;}// DP [i] represents the ith Fibonacci number int [] DP = New Int [n + 1]; dp[0] = 0; dp[1] = 1; for (int i = 2; i <= n; i++) { dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007; } return dp[n]; }}
10-II frog jumping steps
Title: a frog can jump up one step or two steps at a time. Find out how many jumping methods the frog can jump up an n-step.
The answer needs to take the module 1e9+7 (1000000007). If the initial result is 1000000008, please return 1.
Example 1:
Input: n = 2 Output: 2
Example 2:
Input: n = 7 Output: 21
Example 3:
Input: n = 0 Output: 1
analysis:
- Combination condition: n=0, n=1, all return 1; The rest are the same as the previous question
public class Solution {
// Method 1: iterative method
public int numWays1(int n) {
if (n == 0 || n == 1) {
return 1;
}
int a = 1;
int b = 1;
int sum = 0;
for (int i = 0; i < n - 1; i++) {
sum = (a + b) % 1000000007;
a = b;
b = sum;
}
return sum;
}
// Method 2: dynamic programming method
public int numWays2(int n) {
if (n == 0 || n == 1) {
return 1;
}
// dp[i] represents the ith Fibonacci number
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007;
}
return dp[n];
}
}
11 minimum number of rotation array
Title: moving the first elements of an array to the end of the array is called array rotation. Enter a rotation of an incrementally sorted array and output the smallest element of the rotation array. For example, if the array [3,4,5,1,2] is a rotation of [1,2,3,4,5], the minimum value of the array is 1.
Example 1:
Input:[3,4,5,1,2] Output: 1
Example 2:
Input:[2,2,2,0,1] Output: 0
analysis:
- Normally increment the array, find an element, determine the target, and use the dichotomy
- Rotate a part of the incremental array to indicate that a part must be sorted incrementally. Define target = right boundary value to divide
- Less than, similar to non rotating binary search = the minimum value is on the left, but because the right boundary is included to determine the target, right=mid
- Greater than, the minimum value is on the right, mid has been checked, left=mid+1
- Equal to, unable to determine whether the minimum value is on the left or right. Move the right boundary forward and cycle again, right - –
- The loop condition left < rightorleft < = right is OK, but the return value must be nums[left], because the minimum value must meet left first
- Return value: two points end, left points to the minimum value of the rotation array, and returns num [left]
public class Solution {
// Minimum value of rotation array
public int minArray(int[] numbers) {
int left = 0;
int right = numbers.length - 1;
// The cycle condition is <; Binary search yes<=
while (left < right) {
int mid = left + (right - left) / 2;
// The array part is rotated, and the target value is changed to the rightmost element of the array
int target = numbers[right];
if (numbers[mid] < target) {
// Middle value < right value = right increment
// The minimum value is on the left, and the mid is obtained
right = mid;
} else if (numbers[mid] > target) {
// Middle value > right value = right decrement
// The minimum value is on the right, and mid cannot be taken
left = mid + 1;
} else {
// Middle value = right value. It is impossible to judge whether it is on the left or right, but the minimum value must be close to the left. Shrink mid = shrink target=right--
right--;
}
}
// The return value is the number of left positions
return numbers[left];
}
}
12 path in matrix
Title: give an m x n two-dimensional character grid board and a string word word. If word exists in the grid, return true; Otherwise, false is returned.
Words must be formed alphabetically by letters in adjacent cells, where "adjacent" cells are those horizontally or vertically adjacent. Letters in the same cell cannot be reused.
For example, in 3 below × The matrix of 4 contains the word "ABCCED" (the letters in the word are marked).
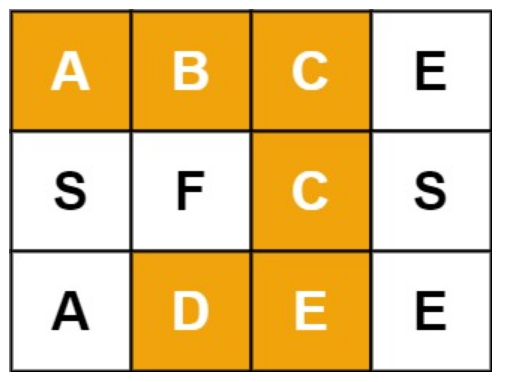
Example 1:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" Output: true
Example 2:
Input: board = [["a","b"],["c","d"]], word = "abcd" Output: false
Tips:
1 <= board.length <= 200 1 <= board[i].length <= 200 board and word It consists of upper and lower case letters only
analysis:
- Traverse the two-dimensional array, match to meet the solution of word, and then return. The typical backtracking problem is to traverse deeply and use recursion
- Define a function bfs(char[][] board, char[] word, int row, int col, int k). K is the pointer to traverse word. The function represents the character array of board and word. When it matches to the end of word, it returns true
- Recursion end condition: the row and column pointer is out of bounds or the current character does not match
- Recursive process:
- If the recursion is not over, first judge whether k reaches the end of word. When it reaches the end, it means that the word matches successfully and returns true
- Temporarily reset the current traversal element to '\ 0' to prevent repeated recursion
- Recursive up, down, left and right, as long as there is a matching up, assign a value to the boolean variable res, and experience the process of backtracking assignment
- The element will be reset temporarily and the original value will be set to prevent the element from changing
- Return: res
public class Solution {
public boolean exist(char[][] board, String word) {
char[] words = word.toCharArray();
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (bfs(board, words, i, j, 0)) {
return true;
}
}
}
return false;
}
private boolean bfs(char[][] board, char[] word, int row, int col, int k) {
// Recursion failure: out of bounds + matching failure / pruning
if (row < 0 || row >= board.length || col < 0 || col >= board[0].length || board[row][col] != word[k]) {
return false;
}
// Recursive success: not out of bounds + board[row][col] = word[k]+k traverses to the end of the word
if (k == word.length - 1) {
return true;
}
// Pruning: if the recursion is not finished, set the current element as an empty character to prevent repeated access later recursion
board[row][col] = '\0';
// If one of the four directions recursively matches successfully, it is returned to res
boolean res = (bfs(board, word, row + 1, col, k + 1) || bfs(board, word, row - 1, col, k + 1)
|| bfs(board, word, row, col + 1, k + 1) || bfs(board, word, row, col - 1, k + 1));
// Backtracking: returns the pruning original value to the current element
board[row][col] = word[k];
return res;
}
}
13 range of motion of robot
Title: there is a square with m rows and N columns on the ground, from coordinates [0,0] to coordinates [m-1,n-1]. A robot starts to move from the grid of coordinates [0,0]. It can move left, right, up and down one grid at a time (it cannot move outside the grid), nor can it enter the grid where the sum of digits of row coordinates and column coordinates is greater than k. For example, when k is 18, the robot can enter the grid [35, 37], because 3 + 5 + 3 + 7 = 18. But it cannot enter the grid [35, 38], because 3 + 5 + 3 + 8 = 19. How many grids can the robot reach?
Example 1:
Input: m = 2, n = 3, k = 1 Output: 3
Example 2:
Input: m = 3, n = 1, k = 0 Output: 1
Tips:
1 <= n,m <= 100 0 <= k <= 20
analysis:
- How to find the sum of row and column coordinates? Check digitSum to learn how to sum digits
- Method 1: dfs1(boolean[][] visited, int i, int j, int k)
- Recursion end condition:
- Define digitSum to calculate the digit sum of (i,j)
- The numeric subscript is out of bounds or the row / column digit and > k or the row / column position has been accessed
- Recursive work: mark that the location has been accessed
- Recursive return: 1 + right recursion + lower recursion
- Recursion end condition:
- Method 2: dfs2(boolean[][] visited, int i, int j, int sumI, int sumJ, int k)
- Note: set the two-dimensional coordinates (I, J), the digits and law of I: (I + 1)% 10 = = 0? Sumi - 8: Sumi + 1. Just give me an example
- Method 1 cancels the digitSum function and adds two parameters to the function signature: Sumi and sumj. Use the regular formula to calculate the digit sum. The other steps are the same as method 1
public class Solution {
public int movingCount(int m, int n, int k) {
boolean[][] visited = new boolean[m][n];
return dfs1(visited, 0, 0, k);
// return dfs2(visited, 0, 0, 0, 0, k);
}
// Method 1: depth traversal method
// Clear concept: starting from (0,0), the row and column digits and coordinates < K will only be on the right or lower side of (0,0), and only recursive i+1/j+1 is used each time
private int dfs1(boolean[][] visited, int i, int j, int k) {
// End of recursion: the row and column are out of bounds or have been accessed
if (i >= visited.length || j >= visited[0].length || digitSum(i) + digitSum(j) > k || visited[i][j]) {
return 0;
}
// If it has not been accessed, it is set to true, which means it has been accessed
visited[i][j] = true;
// +1: The current access location is the number of cells that can be accessed, so add 1
// i+1/j+1: the robot starts from (0,0) and all reachable solutions are at the bottom or right, so only recursive i+1 or j+1 is used
return 1 + dfs1(visited, i + 1, j, k)
+ dfs1(visited, i, j + 1, k);
}
// Find the digit sum of row and column coordinates
private int digitSum(int num) {
int sum = 0;
while (num != 0) {
// Find the single digit of a number
sum += num % 10;
// Then find 10 digits, and so on
num = num / 10;
}
return sum;
}
// Method 2: use the law to calculate the digit sum of rows and columns, cancel the digitSum function, and add Sumi and sumj to the function signature
// Set the two-dimensional coordinates (I, J), the digit and law of I: (I + 1)% 10 = = 0? sumI - 8 : sumI + 1
private int dfs2(boolean[][] visited, int i, int j, int sumI, int sumJ, int k) {
if (i >= visited.length || j >= visited[0].length || sumI + sumJ > k || visited[i][j]) {
return 0;
}
visited[i][j] = true;
// Sumi: the digit sum of I. Sumj: digit sum of J
// Carry: the digits from 9 to 10 and 9 and 2 indicate that after carry, the digit sum is the sum of the previous round of sum-8
// No carry: the digits from 8 to 9 and 8 and 9 indicate no carry. The digit sum is sum+1 of the previous round
return 1 + dfs2(visited, i + 1, j, (i + 1) % 10 == 0 ? sumI - 8 : sumI + 1, sumJ, k)
+ dfs2(visited, i, j + 1, sumI, (j + 1) % 10 == 0 ? sumJ - 8 : sumJ + 1, k);
}
}
14 cutting rope I
Title: here is a rope with length n. please cut the rope into m segments of integer length (M and N are integers, n > 1 and M > 1). The length of each segment of rope is recorded as k[0],k[1]... k[m-1]. Excuse me, k[0] × k[1]… × What is the maximum possible product of k[m-1]? For example, when the length of the rope is 8, we cut it into three segments with lengths of 2, 3 and 3 respectively. At this time, the maximum product is 18.
Example 1:
input: 2 output: 1 explain: 2 = 1 + 1, 1 × 1 = 1
Example 2:
input: 10 output: 36 explain: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
Tip: n up to 58
2 <= n <= 58
analysis:
- Rule: when the rope is divided into multiple segments with length 3 as much as possible, the product is the largest, Proof of solution to the problem of Li Kou K
- Let n/3=a, n%3=b
- Remainder 0: the description is exactly divided into 3 segments, res = 3 ^ a
- The remainder is 1: if you want the maximum value, change 3 of the penultimate paragraph + 1 of the penultimate paragraph to 2 + 2, because 3 × 1<2 × 2,res = 3 ^ (a-1) × (2 × 2)
- The remainder is 2: res = 3^(a) × two
public class Solution { // Method: mathematical law method public int cuttingRope(int n) {/ / topic specification: 2 < = n < = 58 if (n < = 3) {return n - 1;}// Find the segments where n can be divided into 3, int a = n / 3// Find the remainder of the last paragraph 3 after n trisection, int b = n% 3// if (b == 0) {/ / if the remainder is 0, return 3^a directly as the maximum product return (int) math.pow (3, a);} Else if (b = = 1) {/ / remaining 1, convert 3 in the penultimate paragraph after trisection + 1 in the last paragraph to 2 times 2, because 3 * 1 < 2 * 2 return (int) math.pow (3, a - 1) * (2 * 2);}// For the remaining 2, directly return 3^a*(2). The last paragraph does not need to be split return (int) math pow(3, a) * (2); }}
14 cutting rope II
Title: here is a rope with length n. please cut the rope into m segments of integer length (M and N are integers, n > 1 and M > 1). The length of each segment of rope is recorded as k[0],k[1]... k[m - 1]. Excuse me, k[0] × k[1]… × What is the maximum possible product of k[m - 1]? For example, when the length of the rope is 8, we cut it into three segments with lengths of 2, 3 and 3 respectively. At this time, the maximum product is 18. The answer to this question needs to take the module 1e9+7 (100000007). If the initial result is 100000008, please return 1. The difference between this question and the previous one is that the product will cross the boundary!
Example 1:
input: 2 output: 1 explain: 2 = 1 + 1, 1 × 1 = 1
Example 2:
input: 10 output: 36 explain: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
Tip: n here to 1000
2 <= n <= 1000
analysis:
-
Skill: a = the number of segments divided into 3 - 1, and finally judge the result multiplication according to the remainder b
-
Method 1: cyclic remainder method, each time multiplied by a base is the remainder
-
Method 2: dichotomous remainder method. The odd number is exactly 1. The remainder is calculated when there are only odd numbers, and the base is updated when there are even numbers
public class Solution {
// Method 1: cyclic remainder
public int cuttingRope1(int n) {
if (n <= 3) {
return n - 1;
}
int b = n % 3;
int p = 1000000007;
long rem = 1;
long x = 3;
// a initializes the number of segments with n divided by 3 - 1
int a = n / 3 - 1;
// Cyclic remainder: every time rem%p
for (int i = 1; i <= a; i++) {
rem = (rem * x) % p;
}
// At this time, n there is a segment 3 and remainder (0 or 1 or 2)
if (b == 0) {
// The remainder is 0, multiply by 3 directly
return (int) (rem * (3) % p);
} else if (b == 1) {
// The remainder is 1, 3 + 1 is changed to 2 + 2 because 3 * 1 < 2 * 2
return (int) (rem * (2 * 2) % p);
} else {
// The remainder is 2, and the maximum value of 3 + 2 is 3 * 2
return (int) (rem * (3 * 2) % p);
}
}
// Method 2: dichotomy for remainder
public int cuttingRope2(int n) {
if (n <= 3) {
return n - 1;
}
int b = n % 3;
int p = 1000000007;
long rem = 1;
long x = 3;
// Dichotomy for remainder: odd power calculates the remainder, and even power updates the base
for (int a = n / 3 - 1; a > 0; a /= 2) {
if (a % 2 != 0) {
rem = (rem * x) % p;
}
x = (x * x) % p;
}
if (b == 0) {
return (int) (rem * (3) % p);
} else if (b == 1) {
return (int) (rem * (2 * 2) % p);
} else {
return (int) (rem * (3 * 2) % p);
}
}
}
15 number of 1 in binary
Title: please implement a function to input an integer (in the form of binary string) and output the number of 1 in the binary representation of the number. For example, representing 9 as binary is 1001, and 2 bits are 1. Therefore, if you enter 9, the function outputs 2.
Example 1:
Input: 0000000000000000000000001011 Output: 3 Explanation: there are three digits in the binary string 0000000000000000000000000000001011 '1'.
Example 2:
Input: 000000000000000000000000000000000000000000000 Output: 1 Explanation: in the binary string 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 '1'.
Example 3:
Input: 11111111111111111111111111111111101 Output: 31 Explanation: there are 31 bits in the input binary string 11111111111111111111111111111101 '1'.
Tips:
- The input must be a binary string of length 32.
analysis:
- Since n is binary, it must be thinking & or | equipotential operation. Count the number of 1 in N, using n = n & (n-1) until the end of n=0 cycle, which is the number of 1
- For example:
- n=111,n-1=110,n &= n-1,n=110,res+1
- n=110,n-1=101,n &= n-1,n=100,res+1
- n=100,n-1=010,n &= n-1,n=000,res+1
- n=000, the cycle ends and res is returned
public class Solution {
// Method: n& (n-1)
public int hammingWeight(int n) {
int res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
}
}
16 integer power of value
Title: realize pow(x, n), that is, calculate the N-power function of X (i.e., xn). Library functions must not be used and large numbers do not need to be considered.
Example 1:
Input: x = 2.00000, n = 10 Output: 1024.00000
Example 2:
Input: x = 2.10000, n = 3 Output: 9.26100
Example 3:
Input: x = 2.00000, n = -2 Output: 0.25000 Explanation: 2-2 = 1/22 = 1/4 = 0.25
Tips:
-100.0 < x < 100.0-231 <= n <= 231-1-104 <= xn <= 104
analysis:
- Let any decimal positive integer n whose binary is bmbm-1... b3b2b1, then n=20b1+ 21b2+ 22b3 +... 2m-1b
- xn=xb1+x2b2+x4b3 +..., note 20+x1+x2 +... = xi-1 and b0+b1+b2 +... = bi
- Calculation xi-1: x=x per cycle
- Calculate bi
- =1. Multiply the result by xi-1
- =0, result unchanged = result × one
public class Solution { public double myPow(double x, int n) { if (x == 0) { return 0; } // B points to the power. When n = − 2147483648, n=-n will overflow, so B is a long type, long b = n// Return value initialization: Double res = 1.0// Power if when n is negative (n < 0) {x = 1 / X; b = - B;}// However, after power B judges the leftmost binary bit, end while (b! = 0) {/ / calculate whether the rightmost binary bit of B is 0 or 1 / / the rightmost binary bit of B is 1, multiplied by X if ((B & 1) = = 1) {res * = x;} Else {/ / b the rightmost binary is 0, multiplied by 1 res * = 1;}// x=x^2 x = x * x; // B shift the binary bit to the right by one bit, because at this time, b=|b|, signed or unsigned right shift is OK, b > > = 1;} return res; }}
17 print 1 to maximum n digits
Title: enter the number N and print out the n-digit decimal number from 1 to the maximum in order. For example, if you enter 3, 1, 2 and 3 will be printed up to the maximum 3 digits 999.
Example 1:
input: n = 1 output: [1,2,3,4,5,6,7,8,9]
analysis:
- Determine the boundary value of N digits? n=1, boundary = 10, n=2, boundary = 100, and so on
- Since printing starts from 1, an array of boundary - 1 bits is generated, and each time it is assigned i+1
public class Solution { // Method 1: calculate the boundary value public int[] printNumbers1(int n) {/ / calculate the maximum boundary int boundary = 1; for (int i = 1; I < = n; I + +) {/ / multiply by 10 boundary * = 10 each time;}// Define a return value result int [] res = New Int [boundary - 1]; for (int i = 0; i < res.length; i++) { res[i] = i + 1; } return res; } // Method 2: use the library function to calculate the boundary value public int [] printnumbers2 (int n) {/ / 10 ^ n-1 is the maximum number of N digits = array length int [] res = New Int [(int) math.pow (10, n) - 1]; for (int i = 0; I < res.length; I + +) {/ / the array element is 1 larger than the index, because the number starts from 1. Res [i] = I + 1;} return res; }}
18 delete linked list node
Title: given the head pointer of the one-way linked list and the value of a node to be deleted, define a function to delete the node. Returns the head node of the deleted linked list.
**Note: * * this question is different from the original one
Example 1:
input: head = [4,5,1,9], val = 5 output: [4,1,9]explain: Given the second node with a value of 5 in your linked list, after calling your function, the linked list should be 4 -> 1 -> 9.
Example 2:
input: head = [4,5,1,9], val = 1 output: [4,5,9]explain: Given the third node with a value of 1 in your linked list, after calling your function, the linked list should be 4 -> 5 -> 9.
explain:
- Ensure that the values of nodes in the linked list are different from each other
- If you use C or C + + language, you do not need to free or delete the deleted node
analysis:
- Method 1: double pointer version, pre and cur
- Method 2: single pointer version, cur traverses to the previous position of the node to be deleted
public class Solution { // Method 1: double pointer public listnode deletenode1 (listnode head, int VAL) {/ / 1. Judge whether the head is the node to be deleted. Instead, initialize cur and pre if (head = = null) {return null;} if (head.val == val) { return head.next; } // 2. Initialize pre and cur listnode pre = head; ListNode cur = head. next; // 3. Cur traversal until cur Val = = Val node while (cur!=null & & cur. Val! = Val) {pre = cur; / / since cur points to the next node, the while condition increases cur!=null cur = cur. Next;}// 4. Loop out, when cur= When null, it must point to the node to be deleted if (cur!=null) {pre.next = cur.next;} return head; } // Method 2: single pointer version public listnode deletenode2 (listnode head, int VAL) {if (head = = null) {return null;} if (head.val == val) { return head.next; } ListNode cur = head; // Cur traverses to the previous position of the node to be deleted while (cur. Next! = null & & cur. Next. Val! = Val) {cur = cur. Next;} if (cur.next != null) { cur.next = cur.next.next; } return head; }}
19 regular expression matching
Title: please implement a function to match package '‘ And '*'. Character 'in mode‘ Represents any character, and '*' indicates that the character before it can appear any time (including 0 times). In this question, matching means that all characters of the string match the whole pattern. For example, the string "aaa" matches the patterns "a.a" and "ab*a c * a", but not "aa.a" and "ab*a".
Example 1:
input:s = "aa"p = "a"output: false explain: "a" Cannot match "aa" The entire string.
Example 2:
input:s = "aa"p = "a*"output: true explain: because '*' Represents the one that can match zero or more preceding elements, The preceding element here is 'a'. Therefore, the string "aa" Can be considered 'a' Again.
Example 3:
input:
s = "ab"
p = ".*"
output: true
explain: ".*" Indicates that zero or more can be matched('*')Any character('.').
Example 4:
input: s = "aab" p = "c*a*b" output: true explain: because '*' Represents zero or more, here 'c' Is 0, 'a' Be repeated once. So you can match strings "aab".
Example 5:
input: s = "mississippi" p = "mis*is*p*." output: false s May be empty and contain only from a-z Lower case letters. p May be empty and contain only from a-z Lower case letters and characters . and *,No continuous '*'.
analysis:
- Status array: let the two-dimensional array dp[m+1][n+1], and m and N are the lengths of s and p
- Special note: dp[i][j] indicates the character with s subscript as s[i-1], and p subscript as p[j-1]
- Initialization: dp[i][j] indicates whether the first I characters of s and the first j characters of p match
- dp[0][0]=true, indicating that the first 0 characters of s and p are empty strings and must match
- If s is an empty string and the even subscript of p is ∗ * No, that's a match
- State transition:
- p.charAt(j - 1) = '*', there are three matching cases
- dp[i][j - 2], 0 times for p[j-2]
- (DP [I - 1] [J] & & s.charat (I - 1) = = p.charat (J - 2), p[j-2] appears once, and the characters pointed to by current i-1 and j-2 are the same
- dp[i - 1][j] && p.charAt(j - 2) == '.', Most special case: P [J-2] = When p [J-1] = *, it is known to be universal matching according to conditions
- p.charAt(j - 1) != '*', There are two matches
- DP [I - 1] [J - 1] & & s.charat (I - 1) = = p.charat (J - 1), the previous elements match and the current element is the same
- dp[i - 1][j - 1] && p.charAt(j - 1) == '.', All previous elements match and the current element of P is
- p.charAt(j - 1) = '*', there are three matching cases
- Return value: dp[m][n]
public class Solution {
// Most intuitive version
public boolean isMatch(String s, String p) {
int m = s.length();
int n = p.length();
// dp[i][j] indicates whether the first i-1 characters of s and the first j-1 characters of p match
boolean[][] dp = new boolean[m + 1][n + 1];
// DP [0] [0]: the first 0 characters of S and the first 0 characters of p are empty string = match by default
// Note: because there are more [0] [0], dp[i][j] locates the characters of s[i-1] and p[j-1]
dp[0][0] = true;
// Initialize the first line: when s is an empty string, the even bit of p is * to match
for (int j = 2; j < n + 1; j += 2) {
dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';
}
// state transition
for (int i = 1; i < m + 1; i++) {
for (int j = 1; j < n + 1; j++) {
// When p[j-1] = *, there are three cases
if (p.charAt(j - 1) == '*') {
if (dp[i][j - 2]) {// p[j-2] occurs 0 times, and the length of i and j pointing characters are the same
dp[i][j] = true;
} else if (dp[i - 1][j] && s.charAt(i - 1) == p.charAt(j - 2)) {// p[j-2] appears once, and the current i-1 and j-2 point to the same characters
dp[i][j] = true;
} else if (dp[i - 1][j] && p.charAt(j - 2) == '.') {// Most special case: P [J-2] = P [J-1] = * is universal matching
dp[i][j] = true;
}
} else {// When p[j-1]=* There are two situations
if (dp[i - 1][j - 1] && s.charAt(i - 1) == p.charAt(j - 1)) {// The previous elements match before and the current element is also compatible
dp[i][j] = true;
} else if (dp[i - 1][j - 1] && p.charAt(j - 1) == '.') { // All previous elements match and the current element of p is
dp[i][j] = true;
}
}
}
}
return dp[m][n];
}
// Optimize the code with ternary operators to make the code more beautiful and faster
public boolean isMatch1(String s, String p) {
int m = s.length();
int n = p.length();
// dp[i][j] indicates whether the first i-1 characters of s and the first j-1 characters of p match
boolean[][] dp = new boolean[m + 1][n + 1];
// DP [0] [0]: the first 0 characters of S and the first 0 characters of p are empty string = match by default
// Note: because there are more [0] [0], dp[i][j] locates the characters of s[i-1] and p[j-1]
dp[0][0] = true;
// Initialize the first line: when s is an empty string, the even bit of p is * to match
for (int j = 2; j < n + 1; j += 2) {
dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';
}
// state transition
for (int i = 1; i < m + 1; i++) {
for (int j = 1; j < n + 1; j++) {
dp[i][j] = p.charAt(j - 1) == '*' ?
dp[i][j - 2] || dp[i - 1][j] && (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.') :
dp[i - 1][j - 1] && (p.charAt(j - 1) == '.' || s.charAt(i - 1) == p.charAt(j - 1));
}
}
return dp[m][n];
}
}
20 a string representing a numeric value
Title: please implement a function to judge whether the string represents a numeric value (including integer and decimal).
The values (in order) can be divided into the following parts:
- Several spaces
- A decimal or integer
- (optional) an 'e' or 'e' followed by an integer
- Several spaces
Decimals (in order) can be divided into the following parts:
- (optional) one symbolic character ('+' or '-')
- One of the following formats:
- At least one digit followed by a dot '
- At least one digit followed by a dot ', Followed by at least one digit
- A dot ', Followed by at least one digit
Integers (in order) can be divided into the following parts:
- (optional) one symbolic character ('+' or '-')
- At least one digit
Some values are listed as follows:
["+100", "5e2", "-123", "3.1416", "-1E-16", "0123"]
Some non numerical values are listed as follows:
["12e", "1a3.14", "1.2.3", "+-5", "12e+5.4"]
Example 1:
Input: s = "0"Output: true
Example 2:
Input: s = "e"Output: false
Example 3:
Input: s = "."Output: false
Example 4:
Input: s = " .1 "Output: true
Tips:
1 <= s.length <= 20s Only English letters (uppercase and lowercase) and numbers (0-9),plus '+' ,minus sign '-' ,Space ' ' Or point '.' .
analysis:
-
There are too many cases of judging true. We think about judging false and define four Boolean values
- hasNum,hasSign,hasE,hasDot
-
Traversal pointer: index
-
Clear the space before the string, index++
-
While (index < n) judgment
- Judge the numeric part first, until it encounters non numeric or, directly reaches the end of the string, and returns true
- Then judge the non digital part
- Judge E: if there is E before or no number before, return false; Otherwise, hasE=true
- Judge +, -: if there is +, - or there is a number or there is, Return false; Otherwise hasign = true
- Judgment.: If there was one before or with E, return false; Otherwise, Hadot = true
- If you encounter a space, end the loop directly, because index can no longer be equal to n, and the result is false
- index++
-
Clear the space after the string, index++
-
Return: hasnum & & index = = n
public class Solution {
public boolean isNumber(String s) {
int n = s.length();
int index = 0;
boolean hasNum = false;
boolean hasE = false;
boolean hasSign = false;
boolean hasDot = false;
// Clear preceding spaces
while (index < n && s.charAt(index) == ' ') {
index++;
}
while (index < n) {
// 1. Judge the number first
while (index < n && s.charAt(index) >= '0' && s.charAt(index) <= '9') {
hasNum = true;
index++;
}
// If the loop has reached the end of the string
if (index == n) {
break;
}
// 2. Judge the non digital part
if (s.charAt(index) == 'E' || s.charAt(index) == 'e') {
if (hasE || !hasNum) {
return false;
}
hasE = true;
// After E occurs, four situations need to be judged again = reset empty
hasNum = false;
hasDot = false;
hasSign = false;
} else if (s.charAt(index) == '+' || s.charAt(index) == '-') {
if (hasSign || hasNum || hasDot) {
return false;
}
hasSign = true;
} else if (s.charAt(index) == '.') {
if (hasDot || hasE) {
return false;
}
hasDot = true;
} else if (s.charAt(index) == ' ') {// If the middle space is encountered, the loop ends and the index length is judged
break;
} else {
return false;
}
// 3. The pointer moves back
index++;
}
// Clear the following space
while (index < n && s.charAt(index) == ' ') {
index++;
}
// Judgment condition: there are numbers and the index traverses to n
return hasNum && index == n;
}
}
21 adjust array odd before even
Title: enter an integer array and implement a function to adjust the order of numbers in the array so that all odd numbers are in the first half of the array and all even numbers are in the second half of the array.
Example:
Input: nums = [1,2,3,4] Output:[1,3,2,4] Note:[3,1,2,4] It is also one of the correct answers.
analysis:
- Double pointer, i traverses the front and j traverses the back
- i moves backward when encountering non even numbers, and j moves forward when encountering even numbers
- The traversal ends when i=j, because a number does not need to be exchanged, so the loop condition is while (I < J)
public class Solution {
// Double finger Needling: move backward when left is an odd number, and move forward when right is an even number
public int[] exchange(int[] nums) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
while (left < right && (nums[left] % 2) != 0) {
left++;
}
while (left < right && (nums[right] % 2) == 0) {
right--;
}
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
return nums;
}
}
22 the penultimate node in the linked list
Title: enter a linked list and output the penultimate node in the linked list. In order to conform to the habit of most people, this question starts from 1, that is, the tail node of the linked list is the penultimate node.
For example, a linked list has six nodes. Starting from the beginning, their values are 1, 2, 3, 4, 5 and 6. The penultimate node of the linked list is a node with a value of 4.
Example:
Given a linked list: 1->2->3->4->5, and k = 2.Return to linked list 4->5.
analysis:
- The first reaction is to traverse the linked list first, record the length n of the linked list, and then n-k+1 is the linked list to be returned, but this has a high time complexity
- With double pointers, you only need to traverse the array once
- Initialization: both fast and slow point to head
- Fast takes K steps first to ensure that the distance between fast and slow is k units
- Then fast and slow move simultaneously. When fast moves to null, slow points to the penultimate node
- Return slow
public class Solution { public ListNode getKthFromEnd(ListNode head, int k) { ListNode fast = head; ListNode slow = head; // 1. The fast pointer takes K steps while (k > 0) {/ / the fast pointer must judge whether it is null every time. Pay attention to the boundary problem if (fast = = null) {return null;} fast = fast. next; k--; } // 2. When the fast pointer goes to the next node of the end node = null, slow goes to the penultimate node while (fast! = null) {slow = slow.next; fast = fast.next;} return slow; }}
24 reverse linked list
Title: define a function, input the head node of a linked list, reverse the linked list and output the head node of the inverted linked list.
Example:
input: 1->2->3->4->5->NULL output: 5->4->3->2->1->NULL
analysis:
- Iterative method
- Recursive method
public class Solution { // Method 1: iterative method public listnode reverselist1 (listnode head) {listnode cur = head; / / pre only records the previous node of cur and will not use any next node. Listnode pre = null; while (cur! = null) {/ / the ListNode next = cur.next after cur must be recorded first; / / change from cur to cur.next = pre; pre = cur; cur = next;} return pre; } // Method 2: recursive method public listnode reverselist2 (listnode head) {/ / 1. A single node or an empty node is reversed, which is itself if (head = = null | head. Next = = null) {return head;}// 2. Recursion ends at the end of the linked list. At this time, ret is the last non empty node, head is the penultimate non empty node, listnode ret = reverselist2 (head. Next)// 3. There are penultimate and penultimate nodes. Think about the inversion process head next. next = head;// End node reverse pointer head next = null;// The penultimate node next is empty for the upper layer to call return;}}
25 merge two ordered linked lists
Title: enter two incrementally sorted linked lists, merge the two linked lists, and make the nodes in the new linked list still incrementally sorted.
Example 1:
Input: 1->2->4, 1->3->4 Output: 1->1->2->3->4->4
Limitations:
0 <= Linked list length <= 1000
analysis:
- The merging of two ordered linked lists is very similar to merging two ordered arrays. Compare the code Learning + two merging sorting merge process
public class Solution { // Method 1: iterative method public ListNode mergeTwoLists1(ListNode l1, ListNode l2) {/ / set a dummy node to facilitate the return value listnode dummynode = new listnode (- 1); / / cur pointer points to the smaller value node listnode cur = dummynode for each comparison; while (L1! = null & & L2! = null) {/ / judge the smaller value. Cur points to it. If (L1. Val < = L2. VAL) {cur. Next = L1; L1 = L1. Next;} else { cur.next = l2; l2 = l2.next; } // Move cur after judgment cur = cur next; } // At the end of the loop, cur points to the non empty linked list header cur next = (l1 == null) ? l2 : l1; return dummyNode. next; } // Method 2: recursive method public ListNode mergeTwoLists2(ListNode l1, ListNode l2) {/ / recursive end case 1: a linked list traverses to the end if (L1 = = null | L2 = = null) {return L1 = = null? L2: L1;}// Recursion judgment: return the minimum value node into the recursion stack every time if (L1. Val < = L2. VAL) {l1.next = mergetwolists2 (l1.next, L2); / / recursion end condition 2: return the minimum value node of a linked list return L1;} Else {l2.next = mergetwolists2 (L1, L2. Next); / / recursion end condition 2: return the minimum value node of a linked list return l2;}}
Force buckle 88 combines two ordered arrays
public class Solution {
// Method 1: double pointer, traversing two arrays from front to back, requiring auxiliary arrays
public static void merge1(int[] nums1, int m, int[] nums2, int n) {
// temp stores the sorted array each time
int[] temp = new int[m + n];
// p traverses nums1,q traverses nums2, and I traverses temp
int p = 0, q = 0, i = 0;
while (p < m && q < n) {
temp[i++] = nums1[p] < nums2[q] ? nums1[p++] : nums2[q++];
}
while (p < m) {
temp[i++] = nums1[p++];
}
while (q < n) {
temp[i++] = nums2[q++];
}
// Traverse the temp array back to nums1
System.arraycopy(temp, 0, nums1, 0, m + n);
}
// Method 2: double pointer, traverse two arrays from back to front, maximize, and no auxiliary array is required
public static void merge2(int[] nums1, int m, int[] nums2, int n) {
int p = m - 1, q = n - 1, i = m + n - 1;
// Find the big one from back to front and put it into nums1
while (p >= 0 && q >= 0) {
nums1[i--] = nums1[p] < nums2[q] ? nums2[q--] : nums1[p--];
}
// When p < 0, the above traversal ends. At this time, Q has not traversed to 0. Copy nums2 from [0,q+1) to nums1
System.arraycopy(nums2, 0, nums1, 0, q + 1);
}
}
Substructure of 26 tree
Title: input two binary trees a and B to judge whether B is the substructure of A. (the contract empty tree is not a substructure of any tree)

analysis:
- Define a function isContainB to judge whether the subtree with node as the root node contains B
- B if it is null, it means that there is no match across the leaf node, and false is returned
- If A is null or the value of A is not equal to the value of B, false is also returned
- Otherwise, recursion again determines whether left and right are substructures
- Main function judgment
- The title specifies that an empty tree is not A substructure of any tree, so one of A or B is null and returns false
- Otherwise, if one of the three conditions iscontainb (a, b) | issubstructure (A.left, b) | issubstructure (a.right, b) is satisfied, it is a substructure
- Note: isContainB(A, B) only determines whether A and its subtree are substructures of B
public class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
if (A == null || B == null) {
return false;
}
return isContainB(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
}
// Judge whether the root node is enough to contain B
private boolean isContainB(TreeNode root, TreeNode B) {
// You must first judge whether B is empty and return true
if (B == null) {
return true;
}
// If A is empty or the value of A is not equal to the value of B, false is returned
if (root == null || root.val != B.val) {
return false;
}
// Substructure: must be left to left and right to right. It cannot be left-right correspondence
return isContainB(root.left, B.left) && isContainB(root.right, B.right);
}
}
27 image of binary tree
Title: Please complete a function, input a binary tree, and the function outputs its image.

Example 1:
Input: root = [4,2,7,1,3,6,9] Output:[4,7,2,9,6,3,1]
analysis:
- Recursive method: two methods, temporary left child node or preorder traversal method
- Iterative method: two writing methods, stack or queue
public class Solution {
// Method 1: recursive method 1, temporarily storing the left child node
public TreeNode mirrorTree1(TreeNode root) {
if (root == null) {
return null;
}
// Temporary left node
TreeNode left = root.left;
// The left node points to the right node
root.left = mirrorTree1(root.right);
// The right node points to the temporary left node
root.right = mirrorTree1(left);
// Returns the current parent node
return root;
}
// Method 2: recursive method 2. Exchange during preorder traversal
public TreeNode mirrorTree2(TreeNode root) {
if (root == null) {
return null;
}
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
mirrorTree2(root.left);
mirrorTree2(root.right);
return root;
}
// Method 3: iterate with stack
public TreeNode mirrorTree3(TreeNode root) {
if (root == null) {
return null;
}
LinkedList<TreeNode> stack = new LinkedList<>();
stack.push(root);
while (!stack.isEmpty()) {
// Stack top element out of line
TreeNode top = stack.pop();
// To use the stack, you must first enter the stack and then exchange
if (top.left != null) {
stack.push(top.left);
}
if (top.right != null) {
stack.push(top.right);
}
// The left and right child nodes of the outgoing node are exchanged
TreeNode temp = top.left;
top.left = top.right;
top.right = temp;
}
return root;
}
// Method 4: iterate with queue
public TreeNode mirrorTree4(TreeNode root) {
if (root == null) {
return null;
}
LinkedList<TreeNode> queue = new LinkedList<>();
// Root node queue
queue.add(root);
while (!queue.isEmpty()) {
// Current queue out
TreeNode poll = queue.poll();
// To use a queue, you must first exchange and then join the queue
TreeNode temp = poll.left;
poll.left = poll.right;
poll.right = temp;
if (poll.left != null) {
queue.add(poll.left);
}
if (poll.right != null) {
queue.add(poll.right);
}
}
return root;
}
}
28 symmetric binary tree
Title: please implement a function to judge whether a binary tree is symmetrical. If a binary tree is the same as its mirror, it is symmetrical.

Analysis: this problem will have a deep understanding of recursion
- Pass in a root. If it is null, it must be symmetrical and return false
- Otherwise, recursively judge the left and right children of root, symmetry condition:
- left.val=right.val
- left.left=right.right
- left.right=right.left
- If one of the left and right children of root does not meet the above conditions, it is not a symmetric binary tree. The conditions are as follows:
- left.val!=right.val
- The left and right are empty and the other is not empty
class Solution { public boolean isSymmetric(TreeNode root) { if (root == null) { return true; } return recur(root.left, root.right); } private boolean recur(TreeNode left, TreeNode right) { // Recursive success: left and right nodes arrive at null if (left = = null & & right = = null) {return true;}// Recursion failure: one of the left and right nodes reaches null, the other does not arrive, or the values of the left and right nodes are different if (left = = null | right = = null | left. Val! = right. VAL) {return false;}// Recursion: (left, left, right) & & (left, right, left, right) return recurs (left. Left, right. Right) & & recurs (left. Right, right. Left);}}
29 print matrix clockwise
Title: enter a matrix and print out each number in clockwise order from outside to inside.
Example 1:
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]Output:[1,2,3,6,9,8,7,4,5]
Example 2:
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]Output:[1,2,3,4,8,12,11,10,9,5,6,7]
analysis:
- If the array is empty, return an empty one-dimensional array
- Initialize upper left corner coordinates (tR,tC)=(0,0), lower right corner coordinates (DR, DC) = (matrix.length - 1, matrix [0]. Length - 1)
- Initialize res [matrix. Length * matrix [0] Length] and index
- Loop condition while (TR < = Dr & & TC < = DC), because a point can also be assigned when assigned to res
- Special case: tR==dR or tC==dC, simply traverse the assignment
- General situation: ensure clockwise to generate a traversal coordinate (curR,curC)
- Left to right: fix tR first and move curC++
- Top to bottom: fixed dC, moving cur++
- Right to left: fixed dR, moving curC --
- Bottom to top: fix tC, move curR --
- When curr and curc are traversed, the traversal condition is= You can't traverse to the endpoint
public class Solution {
public int[] spiralOrder(int[][] matrix) {
// Enter an empty column and return an empty array
if (matrix.length == 0) {
return new int[0];
}
// Initialize the upper left and lower right coordinates
int tR = 0, tC = 0;
int dR = matrix.length - 1, dC = matrix[0].length - 1;
// Result 2D array size = original array size
int[] res = new int[matrix.length * matrix[0].length];
// Array traversal coordinates
int index = 0;
while (tR <= dR && tC <= dC) {
index = spiralMatrix(matrix, index, res, tR++, tC++, dR--, dC--);
}
return res;
}
/**
* Assign a two-dimensional array clockwise to res
*
* @param index Current res assignment subscript
* @return Next res assignment subscript
*/
private int spiralMatrix(int[][] matrix, int index, int[] res, int tR, int tC, int dR, int dC) {
if (tR == dR) {// If the submatrix has only one row, the columns are copied
for (int i = tC; i <= dC; i++) {
res[index++] = matrix[tR][i];
}
} else if (tC == dC) {// If the submatrix has only one column, the rows are copied
for (int i = tR; i <= dR; i++) {
res[index++] = matrix[i][tC];
}
} else {// General situation
// Realize spiral clockwise printing
int curR = tR;
int curC = tC;
while (curC != dC) {
res[index++] = matrix[tR][curC++];
}
while (curR != dR) {
res[index++] = matrix[curR++][dC];
}
while (curC != tC) {
res[index++] = matrix[dR][curC--];
}
while (curR != tR) {
res[index++] = matrix[curR--][tC];
}
}
return index;
}
}
Stack of 30 min functions
Title: define the data structure of the stack. Please implement a min function that can get the smallest element of the stack in this type. In this stack, the time complexity of calling min, push and pop is O(1).
Example:
MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.min(); --> return -3. minStack.pop(); minStack.top(); --> Return 0. minStack.min(); --> return -2.
Tips:
The total number of calls of each function shall not exceed 20000
analysis:
- Prepare two stacks: dataStack records data and minStack records the minimum value
- Push: the push here is asynchronous stack input. The data stack and the minimum value stack elements do not need to keep the same horizontal line, so the amount of code written is minimal
- Data is added to the data stack every time, and the minimum value stack is only added when the top element of the stack > the value to be added or the minimum value stack is empty
- pop: record the stack element. If it is the same as the minimum stack top element, the minimum stack top will also be out of the stack
- top and min() are normally empty, and then operate
public class MinStack {
// Scheme: the data stack stores data, and the Min stack stores only the elements at the top of the < = min stack each time
private LinkedList<Integer> dataStack;
private LinkedList<Integer> minStack;
public MinStack() {
dataStack = new LinkedList<>();
minStack = new LinkedList<>();
}
public void push(int x) {
// Only the element smaller than the top of the minimum value stack can be entered into the minimum value stack
if (minStack.isEmpty() || x <= minStack.peek()) {
minStack.push(x);
}
dataStack.push(x);
}
public void pop() {
if (dataStack.isEmpty()) {
throw new RuntimeException("MinStack is null,not pop()");
}
int pop = dataStack.pop();
if (pop == min()) {
minStack.pop();
}
}
public int top() {
if (dataStack.isEmpty()) {
throw new RuntimeException("MinStack is null,not top()");
}
return dataStack.peek();
}
public int min() {
if (minStack.isEmpty()) {
throw new RuntimeException("MinStack is null,not min()");
}
return minStack.peek();
}
}
31 push in and pop-up sequence of stack
Title: enter two integer sequences. The first sequence represents the push in order of the stack. Please judge whether the second sequence is the pop-up order of the stack. Assume that all the numbers pushed into the stack are not equal. For example, sequence {1,2,3,4,5} is the stack pressing sequence of a stack, and sequence {4,5,3,2,1} is a pop-up sequence corresponding to the stack pressing sequence, but {4,3,5,1,2} cannot be the pop-up sequence of the stack pressing sequence.
Example 1:
Input: pushed = [1,2,3,4,5], popped = [4,5,3,2,1]Output: true Explanation: we can execute in the following order: push(1), push(2), push(3), push(4), pop() -> 4,push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
Example 2:
Input: pushed = [1,2,3,4,5], popped = [4,3,5,1,2]Output: false Explanation: 1 cannot pop up before 2.
Tips:
0 <= pushed.length == popped.length <= 10000 <= pushed[i], popped[i] < 1000pushed yes popped Arrangement of.
analysis:
- Use a stack to simulate push and pop processes
- Traverse the pushed array and add elements to the stack until the top element of the stack is the same as the element of the popped [i] array
- If it is the same, it will be out of the stack until it is different, so the inner layer is a while loop, not an if judgment
- Return value: whether the simulation war is empty. If it is empty, it means true and the match is successful
public class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
// Use an auxiliary stack to simulate the pushed process and match the popped on the way
LinkedList<Integer> stack = new LinkedList<>();
int i = 0;
for (int num : pushed) {
stack.push(num);
while (!stack.isEmpty() && stack.peek() == popped[i]) {
stack.pop();
i++;
}
}
// If the auxiliary stack is empty after matching, it is true
return stack.isEmpty();
}
}
32 print binary tree 1 from top to bottom
Title: print each node of the binary tree from top to bottom, and the nodes of the same layer are printed from left to right.

public class Solution {
public int[] levelOrder(TreeNode root) {
if (root == null) {
return new int[]{};
}
// Methods: print the binary tree from top to bottom and make use of the first in first out characteristic of the queue
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
ArrayList<Integer> temp = new ArrayList<>();
while (!queue.isEmpty()) {
TreeNode pop = queue.poll();
temp.add(pop.val);
if (pop.left != null) {
queue.add(pop.left);
}
if (pop.right != null) {
queue.add(pop.right);
}
}
int[] res = new int[temp.size()];
for (int i = 0; i < res.length; i++) {
res[i] = temp.get(i);
}
return res;
}
}
32 print binary tree 2 from top to bottom
Title: print the binary tree by layer from top to bottom. The nodes of the same layer are printed from left to right, and each layer is printed to one line. (= binary tree sequence traversal)

analysis:
- This problem is binary tree sequence traversal
public class Solution {
// Difficulty: it is the cyclic condition of temp
public List<List<Integer>> levelOrder(TreeNode root) {
if (root == null) {
return new ArrayList<>();
}
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
List<List<Integer>> res = new ArrayList<>();
while (!queue.isEmpty()) {
// temp stores data for each row
List<Integer> temp = new ArrayList<>();
// The following is wrong: for (int i = 0; I < queue. Size(); i++)
// Because the length of the queue changes inside each loop, you cannot use size as the traversal end condition
for (int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
temp.add(node.val);
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
res.add(temp);
}
return res;
}
}
32 print binary tree from top to bottom 3
Title: please implement a function to print the binary tree in zigzag order, that is, the first line is printed from left to right, the second layer is printed from right to left, the third line is printed from left to right, and so on. (zigzag printing binary tree)

analysis:
- Method 1: in the previous question, use res length to judge the odd and even layers. Res.size()% 2 = = 0 is the odd layer, on the contrary, it is the even layer
- Method 2: parity layered into temp
- Print even layer nodes: head in and tail out, ensuring left to right out
- If there are no even layers, the loop jumps out
- Print even layer nodes: tail in and head out to ensure right to left out
public class Solution { // Method 1: continue the routine of printing binary trees 1 and 2, and use res length to judge parity. Public list < list < integer > > levelorder1 (treenode root) {if (root = = null) {return new ArrayList < > ();} List<List<Integer>> res = new LinkedList<>(); LinkedList<TreeNode> queue = new LinkedList<>(); queue. add(root); While (! Queue. Isempty()) {LinkedList < integer > temp = new LinkedList < > (); for (int i = queue. Size(); I > 0; I --) {/ / the auxiliary linked list stores the nodes of each layer TreeNode node = queue.poll(); / / judge the parity layer by the number of elements of res if (res.size()% 2 = = 0) {/ / for odd layers, enter the queue temp.addlast (node. VAL) from the tail normally;} Else {/ / even layers, enter the queue from the head temp. Addfirst (node. VAL);}// Queue saves the left and right child nodes if (node. Left! = null) {queue. Add (node. Left);} if (node.right != null) { queue.add(node.right); } } res.add(temp); } return res; } // Method 2: add parity hierarchically to the double ended queue public list < list < integer > > levelorder2 (treenode root) {if (root = = null) {return new ArrayList < > ();} List<List<Integer>> res = new LinkedList<>(); LinkedList<TreeNode> dequeue = new LinkedList<>(); dequeue. add(root); While (! Dequeue. Isempty()) {ArrayList < integer > temp = new ArrayList < > (); / / print even layer nodes: head in and tail out, ensuring left to right out for (int i = dequeue. Size(); I > 0; I --) {treenode node = dequeue. Removefirst(); temp. Add (node. VAL); if (node. Left! = null) { dequeue.addLast(node.left); } if (node.right != null) { dequeue.addLast(node.right); } } res.add(temp); // If there are no even layer nodes, jump out of if (dequeue. Isempty()) {break;}// Print even layer nodes: tail in and head out, and ensure that they are out from right to left. Temp = new ArrayList < > ()// Every time temp is replaced, it needs to re point to the new linked list for (int i = dequeue. Size(); i > 0; I --) {treenode node = dequeue. Removelast(); temp. Add (node. VAL); / / enter the node if (node. Right! = null) {dequeue. Addfirst (node. Right);} if (node.left != null) { dequeue.addFirst(node.left); } } res.add(temp); } return res; }}
Post order traversal of 33 binary search tree
Title: enter an integer array to judge whether the array is the post order traversal result of a binary search tree. If yes, it returns true; otherwise, it returns false. Suppose that any two numbers of the input array are different from each other.
Refer to the following binary search tree:
5 / \ 2 6 / \ / \ 1 3 Example 1:
input: [1,6,3,2,5]output: false
Example 2:
input: [1,3,2,6,5]output: true
analysis:
- Post order traversal divides the binary search tree into: post order [left child interval | right child interval | root node] + binary search element property = [less than root node interval | greater than root node interval | root node]
- End of recursion:
- If there is only one element or no element, stop recursion
- Inter partition: if the root node is postmaster [right], use the above properties to find the first subscript j greater than the following node interval. The array can be divided into less than the root node [left,j-1], greater than the root node [j,right-1], and root node [right]
- The judgment interval satisfies the properties of binary search tree:
- Whether the less than root node [left,j-1] satisfies the property of less than root node is realized by traversing the post ordered array in the inter partition step
- Whether the greater than root node [j,right-1] satisfies the greater than root node property. Here, whether < = postmaster [right] is determined by traversing the j-sequenced elements. If the traversal stops, the traversal pointer = right position, then the property satisfies the next level of recursion, otherwise false is returned
- Recursive return: the following three conditions are met at the same time
- If the traversal stops, does the traversal pointer = right position
- The left subtree interval determines whether it is post order traversal
- The right subtree interval determines whether it is post order traversal
public class Solution { public boolean verifyPostorder(int[] postorder) { return recur(postorder, 0, postorder.length - 1); } private boolean recur(int[] postorder, int left, int right) { if (left >= right) { return true; } // The root node is always postorder [right] / / find the subscript of the first > root node from left to back = the first node of the right subtree int i = left; while (postorder[i] < postorder[right]) { i++; } // Record the right subtree node int j = i// Judge whether the value of < root node while (postorder [i] > postorder [right]) {I + +;} exists in the right subtree [j,right-1]// Subsequent matching succeeds as follows: / / 1 Whether the pointer I reaches the root node right / / 2 Left child interval meets / / 3 The right child interval satisfies return I = = right & & recur (poster, left, J - 1) & & recur (poster, j,right-1);}}
34 paths with a value in a binary tree
Title: enter a binary tree and an integer, and print out all paths where the sum of node values in the binary tree is the input integer. A path is formed from the root node of the tree down to the leaf node.
Example:
Given the following binary tree, and target and target = 22,
5 / \ 4 8 / / \ 11 13 4 / \ / \ 7 2 5 1
return:
[ [5,4,11,2], [5,8,4,5]]
analysis:
- Use the medium order traversal, use the path linked list to record each path, and add the result set if the element sum is target
- If the following three conditions are met: add the current path to the result set
- target == 0
- root.left == null
- root.right == null
- Backtracking requires removing the element at the end of the path
public class Solution { private List<List<Integer>> res = new LinkedList<>(); private LinkedList<Integer> path = new LinkedList<>(); public List<List<Integer>> pathSum(TreeNode root, int target) { recur(root, target); return res; } private void recur(TreeNode root, int target) { if (root == null) { return; } // Preorder traversal: first record the current node value into path add(root.val); target -= root. val; // Join result set condition: target = = 0 & & root left == null && root. Right = = null if (target = = 0 & & root. Left = = null & & root. Right = = null) {/ / new ArrayList < > (path) forms a new linked list and puts it into the result set res.add (New ArrayList < > (path));} if (root.left != null) { recur(root.left, target); } if (root.right != null) { recur(root.right, target); } // Backtracking needs to remove the end of path element path removeLast(); }}
35 copy of complex linked list
Title: please implement the copyRandomList function to copy a complex linked list. In a complex linked list, each node has a next pointer to the next node and a random pointer to any node or null in the linked list.
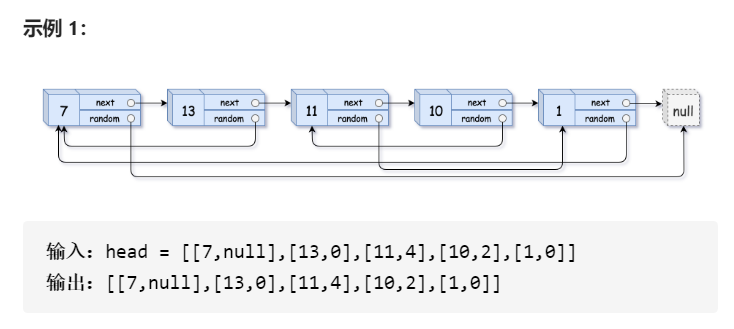
Analysis: the difficulty is how to record the random pointer
- For the first traversal, use map < node to copy the node >
- In the second traversal, take out the value in the map and point to the next and random corresponding to its key
- At the end of the second traversal, return map get(head)
public class Solution { // Map method public node copyrandomlist (node head) {if (head = = null) {return null;} Node cur = head; Map<Node, Node> map = new HashMap<>(); while (cur != null) { map.put(cur, new Node(cur.val)); cur = cur.next; } // Cur re points to head cur = head; while (cur != null) { map.get(cur).next = map.get(cur.next); map.get(cur).random = map.get(cur.random); cur = cur.next; } return map. get(head); }}
36 binary search tree and bidirectional linked list
Title: enter a binary search tree and convert the binary search tree into a sorted circular two-way linked list. It is required that no new node can be created, and only the node pointer in the tree can be adjusted.
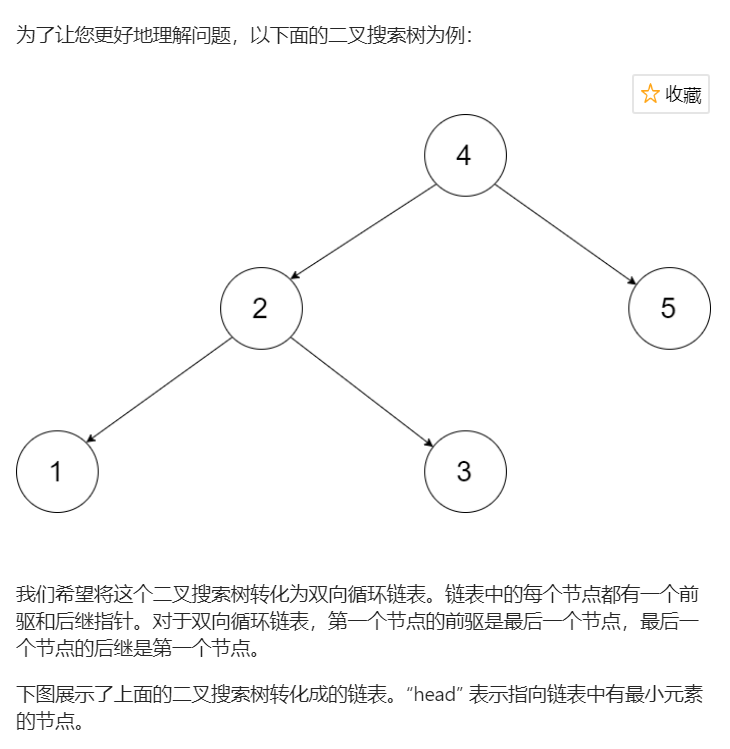
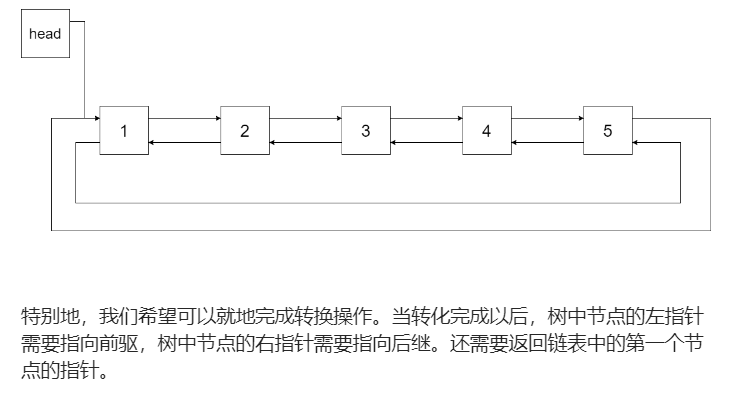
Analysis: it seems difficult, but it is actually very simple. The binary search tree is transformed into a circular two-way linked list arranged from small to large. From small to large, it prompts us to traverse the binary search tree in medium order
- Since the header pointer changes after root forms a two-way linked list, two global variables, pre and head, are defined
- Define a middle order traversal dfs to convert the binary search tree into a two-way linked list
- Change pre and head to convert bidirectional linked list into circular linked list
- Return head
public class Solution { private Node pre; private Node head; public Node treeToDoublyList(Node root) { if (root == null) { return null; } // Middle order traversal forms a two-way linked list dfs(root)// Update the head and tail pointers to form a circular linked list head left = pre; pre. right = head; return head; } private void dfs(Node cur) { if (cur == null) { return; } // Order traversal in binary search tree: ensure from small to large dfs(cur.left)// Update pre if (pre = = null) {/ / current cur is head, head = cur;} Else {/ / pre exists, update the right pointer of pre, pre.right = cur;}// Update cur left = pre; pre = cur; dfs(cur.right); }}
37 serialization and deserialization binary tree
Title: please implement two functions to serialize and deserialize binary trees respectively.
You need to design an algorithm to realize the serialization and deserialization of binary tree. There is no restriction on the execution logic of your sequence / deserialization algorithm. You only need to ensure that a binary tree can be serialized into a string and deserialize the string into the original tree structure.
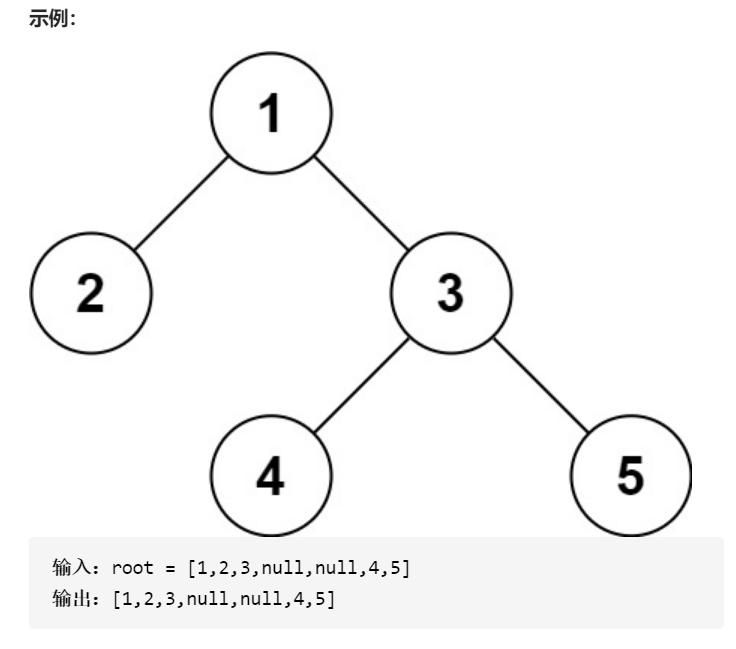
analysis:
Serialization: the specified format is in the form of [x,x,x,x], which is spliced with strings to form []
- Hierarchy traversal, initialization result string [, and the root node will be put into the queue if it is not empty
- Traverse the queue, queue header element out of the queue, and record node
- node!=null, add node. To the result string Val +, and the left and right children of node are in the queue
- node==null, add node to string condition,
- After traversal, delete the comma at the end and return the result string]
Deserialization:
- Delete the beginning and end of the string [] (if there is only [], return null directly), and divide it into character arrays according to
- Form a root node whose value is the first in the character array
- The character array is traversed hierarchically, and the root node enters the queue first; The traversal character array pointer index starts from 1 because the root node has been generated and does not need to be traversed
- Queue element out of queue record node
- If the character array element is not null, node left/node. Right exists and is generated according to the current character array value; At the same time, add node to the queue left/node. right
- Character array element is null, traversing pointer index++
- Return root node
public class Solution { // Serialize the binary tree and return public string Serialize (treenode root) {if (root = = null) {return "[];} in the format specified by the force buckle StringBuilder sb = new StringBuilder ("["); LinkedList < treenode > queue = new LinkedList < > (); queue. Add (root); while (! Queue. Isempty()) {treenode node = queue. Poll(); / / node value is not null if (node! = null) {sb. Append (node. VAL). Append (",") ; // The queue can release the left and right nodes of the queue node each time, because the root is already a binary tree queue add(node.left); queue. add(node.right); } Else {/ / the node value is null, and the result string is added with null +, sb. Append ("null,");}}// Delete the last comma sb deleteCharAt(sb.length() - 1); sb. append("]"); return sb. toString(); } // Deserialize binary tree public treenode deserialize (string data) {if (data. Equals ("[])) return null; string [] split = data. Substring (1, data. Length() - 1). Split (", "); treenode root = new treenode (integer. ParseInt (split [0]); queue < treenode > queue = new LinkedList < treenode > () {add (root) ; }}; // The root node has been generated. The traversal pointer starts from the 1 subscript. Int index = 1; while (!queue.isEmpty()) { TreeNode node = queue.poll(); if (!split[index].equals("null")) { node.left = new TreeNode(Integer.parseInt(split[index])); queue.add(node.left); } // Filter out null index + + in the character array; if (!split[index].equals("null")) { node.right = new TreeNode(Integer.parseInt(split[index])); queue.add(node.right); } index++; } return root; }}
38 arrangement of strings
Title: enter a string and print out all the arrangements of characters in the string.
You can return this string array in any order, but there can be no duplicate elements.
Example:
Input: s = "abc"Output:["abc","acb","bac","bca","cab","cba"]
analysis:
- The string s given by the title has duplicate elements. Use set to judge whether it is a duplicate element. If so, abandon the current cycle, because the repeated arrangement has been calculated for the first time, and there is no need to calculate the arrangement repeatedly
- Define global variables: character array cs, result set linked list res
- Convert s into character array, assign cs, and define a depth traversal function dfs for recursion
- Recursion end condition: when traversing the pointer index and recursing to the cs last element, the current sorting result is added to res
- Recursion: defines a hash set to record whether the current element has entered the arrangement,
- Once entered, it will jump out of the current cycle and start the next cycle
- No entry, set record
- Execute the three most critical lines of code:
// Swap, fix cs[i] in the index bit swap(i, index)// Recursively fix the position DFS of subsequent index+1 (index+1)// Swap back array order swap(i, index)
public class Solution {
private char[] cs;
private List<String> res = new LinkedList<>();
public String[] permutation(String s) {
cs = s.toCharArray();
dfs(0);
// The result list is converted to a string array list ToArray (target array constructor)
return res.toArray(new String[0]);
}
private void dfs(int index) {
// End of recursion: traverse to the end of cs array, add result set, and end of recursion
if (index == cs.length - 1) {
res.add(String.valueOf(cs));
return;
}
HashSet<Character> set = new HashSet<>();
// Traverse the exchange from the element after index
for (int i = index; i < cs.length; i++) {
// In this theory, if repeated characters appear in recursion, paper cutting will jump out of the current cycle
if (set.contains(cs[i])) {
continue;
}
// In this theory, there are no duplicate elements in recursion. Add set to the next round of recursion
set.add(cs[i]);
// Swap, fix cs[i] in the index bit
swap(i, index);
// Recursively fix the position of subsequent index+1
dfs(index + 1);
// Swap back array order
swap(i, index);
}
}
private void swap(int a, int b) {
char temp = cs[a];
cs[a] = cs[b];
cs[b] = temp;
}
}
39 number of occurrences exceeding half in the array
Title: a number in the array appears more than half the length of the array. Please find out this number.
You can assume that the array is non empty and that there are always many elements in a given array.
Example 1:
input: [1, 2, 3, 2, 2, 2, 5, 4, 2] output: 2
analysis:
- Moore voting method
- Initialization: cur records the current array and count records the number of occurrences of the current number
- Processing: traversing the array
- When count==0, update cur==num
- After updating cur, if cur==num is encountered again, count+1; Otherwise, count-1
- Return: cur is returned at last
- Sorting method
- If the number of times in the array exceeds half, it must be in the middle of the sorted array. You can directly return to the middle
- Hash method
- Traverse the array, use the hash table to count < elements, times >, and compare the maximum number of times
- Traverse the hash table and get the key with the maximum number of times, that is, the number with more than half of the times
public class Solution { // Method 1: molar voting method / / if the number of occurrences exceeds half, it will not be offset, The last thing left must be public int majorityelement (int [] Num) {int cur = 0, count = 0; for (int num: Num) {/ / count = 0, indicating that cur needs to be updated to the current number if (count = = 0) {cur = num;}// Cur meets the same number, count+1; Otherwise, count-1 if (cur = = Num) {count + +;} else { count--; } } return cur; } // Method 2: sorting method public int majortyelement1 (int [] Num) {arrays. Sort (Num); / / because there must be more than half of the numbers in the array, the intermediate element must be its return num [num.length / 2];}// Method 3: hashing public int majoritylement2 (int [] Num) {map < integer, integer > map = new HashMap < > (); int maxcount = 1; / / map is saved (element, number of occurrences), and the maximum number of occurrences is recorded for (int num: Num) {if (! Map. Containskey (Num)) {map.put (Num, 1);} else { map.put(num, map.get(num) + 1); maxCount = Math.max(maxCount, map.get(num)); } } // Traverse the map and return the maximum number of keys for (map. Entry < integer, integer > entry: map. Entryset()) {if (entry. Getvalue() = = maxcount) {return entry. Getkey();}} throw new RuntimeException("not element"); }}
40 minimum number of k
Title: enter the integer array arr to find the minimum k number. For example, if you enter 8 numbers: 4, 5, 1, 6, 2, 7, 3 and 8, the minimum 4 numbers are 1, 2, 3 and 4.
Example 1:
Input: arr = [3,2,1], k = 2 Output:[1,2] perhaps [2,1]
Example 2:
Input: arr = [0,1,2,1], k = 1 Output:[0]
Limitations:
0 <= k <= arr.length <= 100000 <= arr[i] <= 10000
analysis:
- Priority queue method
- Find the minimum number of k, and use the large root heap. The number of large root heaps is k
- Store the first k elements of the array into the large root heap
- Start to traverse the array from the subscript of the k+1 element. When the heap top > current element is encountered, the large root heap will be out of the queue, and the current element will be in the queue
- Finally, create a result array, put the large root heap data into the result array and return the result array
- Quick sort idea: the idea of quick sort benchmark can be used to find K numbers. If the benchmark is the next number of the first k numbers, after dividing the interval, the returned array is on the left
- For each interval division, the benchmark is arr[l]. Through the while cycle, the interval is divided into arr[l,i],arr[i],arr[i+1,r], where arr[i]=arr[l]
- If I > k, the first k numbers are on the left, and the left interval is returned recursively
- If I < K, it indicates that the first k numbers are on the right, and recursively returns the right interval
- If i==k, it means that the first k numbers are the left range. Copy and return
public class Solution {
// Method 1: priority queue
public int[] getLeastNumbers1(int[] arr, int k) {
// Finding the minimum number of k and creating a large root heap is the simplest thinking
PriorityQueue<Integer> maxQueue = new PriorityQueue<>((a, b) -> b - a);
// The first k numbers of the array are added to the large root heap
for (int i = 0; i < k; i++) {
maxQueue.add(arr[i]);
}
// [k,len-1], if it is smaller than the top of the large root heap, remove the top of the heap and add the element
for (int i = k; i < arr.length; i++) {
if (!maxQueue.isEmpty() && maxQueue.peek() > arr[i]) {
maxQueue.remove();
maxQueue.add(arr[i]);
}
}
// Put the large root heap element into the result array
int[] res = new int[k];
for (int i = k - 1; i >= 0; i--) {
res[i] = maxQueue.remove();
}
return res;
}
// Method 2: quick sort method
public int[] getLeastNumbers(int[] arr, int k) {
if (k >= arr.length) {
return arr;
}
return findKth(arr, 0, arr.length - 1, k);
}
private int[] findKth(int[] arr, int l, int r, int k) {
int i = l;
int j = r;
// while loop, dividing arr into [l, I] < arr [l], arr [l], arr [i + 1, R] > arr [l]
while (i < j) {
// Find the first arr [J] < arr [l]
while (i < j && arr[j] >= arr[l]) {
j--;
}
// Find the first arr [i] > arr [l]
while (i < j && arr[i] <= arr[l]) {
i++;
}
swap(arr, i, j);
}
// Exchange benchmarks arr[l] and arr[i] to ensure interval division
swap(arr, i, l);
// If I > k, the boundary less than k is on the left
if (i > k) {
return findKth(arr, l, i - 1, k);
}
if (i < k) {
return findKth(arr, i + 1, r, k);
}
// If i==k, the first k numbers are all the numbers before the k subscript
return Arrays.copyOf(arr, k);
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
41 median in data stream
Title: how to get the median in a data stream? If an odd number of values are read out from the data stream, the median is the value in the middle after all values are sorted. If an even number of values are read from the data stream, the median is the average of the middle two numbers after all values are sorted.
For example,
[2,3,4] The median is 3 [2,3] The median is (2 + 3) / 2 = 2.5
Design a data structure that supports the following two operations:
void addNum(int num) - Add an integer from the data stream to the data structure. double findMedian() - Returns the median of all current elements.
Example 1:
Input:["MedianFinder","addNum","addNum","findMedian","addNum","findMedian"][[],[1],[2],[],[3],[]]Output:[null,null,null,1.50000,null,2.00000]
Analysis: if it is a sorted array, the median can be calculated directly, but this is a flowing data flow. To reduce the time complexity, you can use two buckets to save the data
- A bucket: the first half of the number is stored, which is a large pile; Bucket B: the last half is the small root pile
- The number of elements in the two buckets is the same. It is required to enter the previous bucket A first, and then enter bucket B after sorting the large root heap of bucket A
- The number of elements in the two buckets is different. It is required to enter bucket B first, and then enter bucket A after sorting the small root heap of bucket B
- The above method: when the total amount of data is odd, bucket B has one more element than bucket A; When the total amount is even, the two barrels are the same length
- Return value: judge whether the number of two barrels is the same. If the number of barrels is the same, return the top element of barrel B. if it is different, return the top of two barrels / 2.0
public class MedianFinder { // A: Save a small number of N, and use the large root heap private queue < integer > A// B: Store a large number of N, and use the small root heap private queue < integer > b; public MedianFinder() { A = new PriorityQueue<>((a, b) -> (b - a)); B = new PriorityQueue<>(); } Public void addnum (int Num) {/ / the two buckets have the same number of elements. It is required to enter the previous bucket a first, and then enter bucket B if (a.size() = = b.size()) {A.add (Num); b.add (a.poll());} Else {/ / the number of elements in the two buckets is different. It is required to enter bucket B first. After sorting the small root heap of bucket B, enter bucket a b.add (Num); A.add (b.poll());}// The above method: when the total amount of data is odd, bucket B has one more element than bucket a; When the total amount is an even number, the two buckets have the same length} public double findmedian() {/ / buckets A and B are the same. Since data is finally added to bucket B, the top element of B is returned. Return a.size() = = b.size()? (a.peek() + b.peek()) / 2.0: b.peek();}}
42 maximum sum of continuous subarrays
Title: enter an integer array. One or more consecutive integers in the array form a sub array. Find the maximum value of the sum of all subarrays. The required time complexity is O(n).
Add: when you encounter a positive number, add it; If a negative number is encountered, it will have a negative effect on the current sub array and, so no negative number will be added!
Example 1:
input: nums = [-2,1,-3,4,-1,2,1,-5,4]output: 6 explain: Continuous subarray [4,-1,2,1] The sum of is 6.
Tips:
1 <= arr.length <= 10^5-100 <= arr[i] <= 100
analysis:
- This problem is suitable for beginners of dynamic programming. The maximum sum of continuous subarrays: when the sum of the first i-1 is > 0, add it; When i-1 and < = 0 are encountered, they are discarded
- Initialization: a dp array with the length of the original array
- dp[i] represents the maximum sum of subarrays of the first I elements, dp[0]=nums[0]
- At the same time, define a max=nums[0], and record the maximum value in the dp array
- State transition: traverse the original array from i=1
- If DP [I-1] < = 0 has a negative impact, give it up, dp[i]=nums[i]
- DP [I-1] > 0, positive impact, dp[i]=dp[i-1]+nums[i]
- Update Max to the maximum of the current dp[i] and max
- Return: max
public class Solution { // Dynamic programming: the easiest way to understand public int maxsubarray1 (int [] Num) {if (num.length = = 1) {return num [0];}// Initialization dp:dp[i] indicates the maximum sum int [] of the first I elements in nums DP = New Int [nums. Length]; dp[0] = nums[0];// The maximum sum of the 0th element is itself / / the maximum value of the initialized maximum sum = nums [0], never 0 or the minimum integer value int max = nums[0]// Traverse the array for (int i = 1; I < num.length; I + +) {/ / the maximum sum of the first i-1 elements is < = 0, which has a negative impact. Discard if (DP [I - 1] < = 0) {DP [i] = num [i];} Else {/ / the maximum sum of the first i-1 elements < = 0, resulting in a positive impact DP [i] = DP [I - 1] + num [i];}// Update max = math max(max, dp[i]); } return max; } // Dynamic programming method: the easiest way to write it. The disadvantage is that the original array is modified and can only be used to brush questions. Public int maxsubarray2 (int [] Num) {int max = num [0]; for (int i = 1; I < num.length; I + +) {if (Num [I - 1] < = 0) {num [i] = num [i];} else { nums[i] = nums[i] + nums[i - 1]; } // The above statement can be replaced by this: num [i] + = math max(nums[i - 1], 0); max = Math. max(nums[i], max); } return max; }}
43 times of 1 in 1 ~ n
Title: enter an integer n and find the number of occurrences of 1 in the decimal representation of N integers 1 ~ n.
For example, the numbers containing 1 in the integers 12, 1 ~ 12 include 1, 10, 11 and 12. 1 appears five times in total.
Example 1:
Input: n = 12 Output: 5
Example 2:
Input: n = 13 Output: 6
analysis:
- Take n as an x-digit number and define
- Low indicates the number of low digit components
- cur represents the number of bits currently pointed to
- High indicates the number composed of high-order numbers
- digit represents 10i-1 of the number on the ith bit pointed to by cur, which is initialized to 100 = 1
- res records each round of traversal
- Traversing the array, obviously high = = 0 & & cur = = 0, the loop ends, and vice versa= 0 || cur != 0 is the while loop condition
- In each traversal, the rule of calculating the number of occurrences of 1 can be found through the above four variables, Derivation process: K divine power buckle problem solution
- cur=0, the number of occurrences of 1 is: high * digit
- cur=1, the number of occurrences of 1 is: high * digit + low + 1
- Cur > 1, the number of occurrences of 1 is: (high + 1) * digit
- Update the previous 4 variables
- Return to: res
public class Solution { public int countDigitOne(int n) { // Initialization: low, cur, high, digit, int, low = 0; int cur = n % 10; int high = n / 10; int digit = 1;// 10^0=1 int res = 0; While (high! = 0 | cur! = 0) {/ / cur has three situations: 0,1, > 1. Use paper to launch these three expressions if (cur = = 0) {res + = high * digit;} else if (cur == 1) { res += high * digit + low + 1; } else if (cur > 1) { res += (high + 1) * digit; } // Update low, cur, high, digit low + = cur * digit; cur = high % 10; high = high / 10; digit *= 10; } return res; }}
44 the number of each digit in the number series
Title: numbers are serialized into a character sequence in the format of 0123456789101112131415. In this sequence, bit 5 (counting from subscript 0) is 5, bit 13 is 1, bit 19 is 4, and so on. Please write a function to find any number corresponding to the nth bit.
Example 1:
Input: n = 3 Output: 3
Example 2:
Input: n = 11 Output: 0
Limitations:
0 <= n < 2^31
analysis: Li Kou K God problem solving learning
-
Initialization: start=1, digit=1, count=(9) × start) × digit=9
-
Determine the number of digits to which the n belongs and the number of digits in the range of digits in which the n belongs
- Using the loop, n subtracts the total number of digits in the digit interval every time until the difference is less than the total number of intervals, and then it jumps out
-
Calculate which number belongs to this digit
- Formula: start + (n - 1) / digit
-
Determine which digit is below the number
-
Formula: (n - 1)% digit
-
-
Note: because you want to locate the number of bits, java uses string Chat location is the most convenient, and then - '0' is the current number of n
-
public class Solution { public int findNthDigit(int n) { // Define the following concepts: digit n, digit num, digit start / / N: 012345678910112, Each digit is recorded as a digit. / / num:10,11,12 is called our common digit, and 11 is the second digit in 10-19. / / digit: the digit 10 is a two digit number, and the digit of 10 is 2, which is recorded as digit. / / start: the starting value of the digit represented by each digit (i.e. 1,10100), which is recorded as start. / / initialize digit, starting from 1. int digit = 1// Initialize start, starting from 1. long start = 1// Number of digits per digit: count=9 × start × Digit, which is obviously initialized to 9 long count=9// Get the digit of N and the start while (n > count) {n - = count; digit + +; start * = 10; / / calculate the next round of count=9 * start * digit count = (9 * start) * digit;}// The while loop above ends, and N becomes the first number under the digit. / / calculate the number n belongs to the digit. long num = start + (n - 1) / digit// Calculate that n is the digit of the digit. Int index = (n - 1)% digit// The return value is specified as int. locate char and then - '0' to return string valueOf(num). charAt(index) - '0'; }}
45 arrange the array into the smallest number
Title: enter a non negative integer array, splice all the numbers in the array into a number, and print the smallest of all the numbers that can be spliced.
Example 1:
input: [10,2]output: "102"
Example 2:
input: [3,30,34,5,9]output: "3033459"
Tips:
0 < nums.length <= 100
explain:
The output result may be very large, so you need to return a string instead of an integer. The spliced number may have a leading 0. The leading 0 does not need to be removed in the final result
analysis:
- When comparing two characters, the comparison rules sorted by small and large are: (x, y) - > (x + y) compareTo(y + x)
- (x + y) < (y + x), then x is sorted in front of Y
- (x + y) > (y + x), then x is sorted after y
- Convert nums array to character array
- Using the library sorting function array Sort() compares the character arrays according to the appealed comparator rules
- Convert the sorted string array into a string, which is the lowest decimal number
public class Solution { public String minNumber(int[] nums) { // Convert nums to string array string [] STRs = new string [nums. Length]; for (int i = 0; i < nums.length; i++) { strs[i] = String.valueOf(nums[i]); } // Press STRs (x + y) CompareTo (y + x) to sort arrays sort(strs, (x, y) -> (x + y).compareTo(y + x)); // Convert the sorted STRs into STR and return StringBuilder sb = new stringbuilder(); for (String str : strs) { sb.append(str); } return sb. toString(); }}
46 translate numbers into characters
Title: given a number, we translate it into a string according to the following rules: 0 into "a", 1 into "b",..., 11 into "l",..., 25 into "z". A number may have multiple translations. Please program a function to calculate how many different translation methods there are for a number.
Example 1:
input: 12258 output: 5 explain: 12258 There are five different translations"bccfi", "bwfi", "bczi", "mcfi"and"mzi"
Tips:
0 <= num < 231
analysis:
- Initialization: the dynamic array dp[i] represents the number of translations ending in xi. The length of dp is n+1. See the notes for the reasons
- State transition:
- Convert num to string
- Traverse the string from the third digit
- If subStr can be translated as a whole, dp[i]=dp[i-1]+dp[i-2]
- If subStr cannot be translated as a whole, dp[i]=dp[i-1]
- Overall translation judgment: (substr. CompareTo ("10") > = 0 & & substr compareTo("25") <= 0)
- Return value: return dp[n]
public class Solution { // Dynamic programming: the easiest way to understand public int translateNum1(int num) {/ / convert num to string STR = string.valueof (Num); int n = str.length(); / / DP [i] represents the number of translations ending in xi, and DP length is n+1 / / initialize dp[0]=dp[1]=1, indicating "no number" and "the number of translations in the first place of STR" / / dp[0]=1 how to push? Because dp[1]=1,dp[2] is either = 1 or = 2. When dp[2]=2, DP [0] must be 1 int [] DP = New Int [n+1]; dp[0]=dp[1]=1; // Traverse for (int i = 2; I < = n; I + +) {/ / split the string composed of xi-1+xi substr string substr = str.substring (I - 2, I); / / if substr can be translated as a whole, dp[i]=dp[i-1]+dp[i-2] / / if substr cannot be translated as a whole, DP [i] = DP [I-1] int count = (substr.compareto ("10") >= 0 && subStr. compareTo("25") <= 0) ? dp[i - 1] + dp[i - 2] : dp[i - 1]; dp[i] = count; } return dp[n]; } // Dynamic programming: convert the DP array of the above method into two iterations public int translatenum2 (int Num) {string STR = string.valueof (Num); int n = str.length(); int a = 1; / / indicates DP [I-2] int b = 1; / / indicates DP [I-1] for (int i = 2; I < = n; I + +) {string substr = str.substring (I - 2, I); int count= (subStr.compareTo("10") >= 0 && subStr. compareTo("25") <= 0) ? a + b : b; a = b; b = count; } // Return to B, because B saves count every time. Return B;}}
47 maximum value of gifts
Title: there is a gift in each grid of an m*n chessboard, and each gift has a certain value (value greater than 0). You can start from the upper left corner of the chessboard to take the gifts in the grid, and move one grid to the right or down at a time until you reach the lower right corner of the chessboard. Given the value of a chessboard and the gifts on it, please calculate the maximum value of gifts you can get?
Example 1:
input: [ [1,3,1], [1,5,1], [4,2,1]]output: 12 explain: Path 1→3→5→2→1 You can get the most valuable gift
Tips:
0 < grid.length <= 2000 < grid[0].length <= 200
analysis:
- Understand the meaning of the topic: the maximum value of the current coordinate comes from the maximum value on its left or top + itself. Obviously, it is dynamic planning. Just find out the state transition
- Initialization: dp[m][n],m and N are the number of rows and columns of the grid respectively
- dp[0][0]=grid[0][0], because the maximum value of the origin is itself
- First line: dp[i][j] = dp[i][j - 1] + grid[i][j];
- First column: dp[i][j] = dp[i - 1][j] + grid[i][j];
- State transition: dp[i][j]=max {left, upper} + grid[i][j]
- Return value: dp the last element
public class Solution { // Dynamic programming: the easiest way to understand public int maxValue1(int[][] grid) {/ / initialize the DP array with the length DP [M] [n] int m = grid.length; int n = grid [0]. Length; int [] [] DP = New Int [M] [n]; / / obviously, the basic state value is: Grid [0] [0] dp[0][0] = grid [0] [0]; / / general state transition: dp[i][j]=Max{dp[i-1][j],dp[i][j-1]}+grid[i][j] / / but there are three special cases: dp[0][0], the first row and the first column for (int i = 0; I < m; I + +) {for (int j = 0; J < n; J + +) {if (I = = 0 & & J = = 0) {/ / special case: skip continue when encountering the origin dp[0][0];} Else if (I = = 0) {/ / special case: the first line DP [i] [J] = DP [i] [J - 1] + grid [i] [J];} Else if (J = = 0) {/ / special case: the first column DP [i] [J] = DP [I - 1] [J] + grid [i] [J];} Else {/ / general state transition: dp[i][j]=Max{dp[i-1][j],dp[i][j-1]}+grid[i][j] DP [i] [J] = math max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]; } } } return dp[m - 1][n - 1]; } // Dynamic programming: efficient writing. The disadvantage is that the original array public int maxvalue2 (int [] [] grid) {int m = grid.length; int n = grid [0]. Length is changed. / / special case: when the first column is encountered, initialize for (int i = 1; I < n; I + +) {grid [0] [i] + = grid [0] [I - 1];}// Special case: when the first row is encountered, initialize for (int i = 1; I < m; I + +) {grid [i] [0] + = grid [I - 1] [0];}// General state transition from [1] [1]; for (int i = 1; I < m; I + +) {for (int j = 1; J < n; j + +) {grid [i] [J] + = math.max (grid [I - 1] [J], grid [i] [J - 1]);}} return grid[m - 1][n - 1]; }}
48 longest substring without duplicate characters
Title: please find the longest substring that does not contain duplicate characters from the string and calculate the length of the longest substring.
Example 1:
input: "abcabcbb"output: 3 explain: Because the longest substring without duplicate characters is "abc",So its length is 3.
Example 2:
input: "bbbbb"output: 1 explain: Because the longest substring without duplicate characters is "b",So its length is 1.
Example 3:
input: "pwwkew"output: 3 explain: Because the longest substring without duplicate characters is "wke",So its length is 3. Please note that your answer must be the length of the substring,"pwke" Is a subsequence, not a substring.
analysis:
- map method: the solution in Zuo Shenshu is easier to understand. Dynamic programming method will be studied in the future
- initialization:
- HashMap < character, integer > record: the current element and the most recent subscript of the current element
- pre = -1: str[i-1] is the previous position of the starting position of the ending non repeating substring, and the initial test value is - 1, that is, the non repeating substring of str[i-1] ends from its left to pre
- len = 0: record the maximum length of non repeating substring in each round, initially 0
- curLen = 0: record the length of non repeating substring in each round, initially 0
- Traversal character array
- Suppose map get(chars[i])=i'
- If I 'is on the right of pre, it means that [i'+1,i] must be a non repeating substring at the end of chars[i]
- Pre points to the rightmost value of i 'and pre every time as the pre value of the next round of traversal chars[i-1]
- So we need to update pre to i‘
- If I 'is on the left of pre, it means that [pre+1,i] must be a non repeating substring ending in chars[i]
- Pre points to the rightmost value of i 'and pre every time as the pre value of the next round of traversal chars[i-1]
- Since pre is larger than i ', there is no need to update it
- Record curLen, record the distance of [pre,i] at this time, and len records the maximum value of each round
- Return to: len
public class Solution { // Method 1: the longest non repeating substring. The most intuitive way to write the map method is public int lengthoflongestsubstring1 (string s) {if (s = = null | s.equals ("") {return 0;}// Convert s into a character array, such as ['a ',' B ',' C ',' a ',' B ',' C ',' B ',' B '] char [] chars = s.tochararray()// Map < this character, the subscript of the last position of this character >, the initialization value is all - 1 HashMap < character, integer > map = new HashMap < > (); for (char c : chars) { map.put(c, -1); } // Pre: STR [I-1] is the previous position of the starting position of the non repeating substring at the end, and the initial test value is - 1 int pre = - 1// Len: record the maximum length of a non repeating substring. / / len initialization 0: it can be understood that the distance between chars[0] and the last occurrence of chars[0] is 0 int len = 0// Curlen: the difference between I and pre / / curlen initialization 0: it can be understood that the difference between the previous position of the substring ending in chars[0] and nonexistent chars[-1] is 0 int curlen = 0; For (int i = 0; I < chars. Length; I + +) {/ / suppose map.get(chars[i])=i '/ / if I' is on the right of pre, it means that [I '+ 1,i] must be a non repeating substring at the end of chars [i]; if (map.get (chars [i]) > = pre) {pre = map.get (chars [i]); / / pre and I' who is on the right, who will update = as the next round of chars[i-1] Curlen = I - map get(chars[i]); } Else {/ / if I 'is on the left of pre, it means that [pre+1,i] must be a non repeating substring at the end of chars [i]; curren = I - pre;}// Len record the maximum value of each round len = math max(len, curLen); // Update the map to record the element and its most recent location put(chars[i], i); } return len; } // Method 2: the map method is changed to a simpler writing method public int lengthoflongestsubstring2 (string s) {if (s = = null | s.equals ("") {return 0;} char[] chars = s.toCharArray(); // The hash table uses a one bit array, which is faster. The ASCII code of characters in the character array does not exceed 127 int [] map = New Int [128]; for (int i = 0; i < 128; i++) { map[i] = -1; } int pre = -1; int len = 0; int curLen; For (int i = 0; I < chars. Length; I + +) {/ / first find the rightmost value of pre and I '; pre = Math.max(pre, map[chars[i]]); / / directly calculate the difference between I and the rightmost element, reduce if, and judge curLen = i - pre. / / record the len length of each round. len = Math.max(len, curLen) ; // Update map [chars [i]] = I;} return len; }}
49 ugly number
Title: we call the number containing only quality factors 2, 3 and 5 Ugly Number. Find the nth Ugly Number in the order from small to large.
Example:
input: n = 10 output: 12 explain: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 It's the top 10 ugly numbers.
explain:
1 It's an ugly number. n Not more than 1690.
analysis:
- Ugly number = the smaller ugly number × A number in (2,3,5):
- Suppose the ugly number Xi = (Xa) × 2 or Xb × 3 or Xc × 5)
- Since Xa, Xb and Xc are all small ugly numbers, if you push forward to the beginning, the condition gives that the first ugly number is 1 and the second ugly number must be a smaller ugly number × (2,3,5) since the second ugly number is known to be 2, it is obvious that the minimum value of (2,3,5) * 1 is equal to 2, and so is the recurrence of the following ugly numbers
- Derived formula:
- General formula: dp[i]=min{dp[a-1]*2,dp[b-1]*3,dp[c-1]*5}
- Pointer backward: DP [A-1] * 2 < = DP [i] < DP [a] * 2
- Pointer backward: DP [B-1] * 3 < = DP [i] < DP [b] * 3
- Pointer backward: DP [C-1] * 5 < = DP [i] < DP [C] * 5
- Note: when the minimum values are the same, the pointer must move back at the same time
- initialization:
- dp[i] represents the i+1 ugly number. The length of dp [] is obviously the parameter n, and the initialization dp[0]=1
- Initialize three pointers. a points to 2 multiples, b points to 3 multiples, and c points to 5 multiples
- State transition: traverse the dp array from the second number
- Since dp[i]=min{dp[a-1]*2,dp[b-1]*3,dp[c-1]*5}, first calculate the value of the next number that each pointer may point to, and select the minimum value, which is dp[i] of this round
- Move the pointer backward. Using the property of DP [A-1] * 2 < = dp[i] < DP [a] * 2, the pointer corresponding to which ni dp[i] is equal to will be moved backward by one bit. Multiple pointers are the same, and multiple pointers will be moved backward by one bit
- Return value: dp[n-1]
public class Solution { // Returns the nth ugly number, Ugly number is a factor containing only 2,3,5 public int nthUglyNumber(int n) {/ / initialization: three pointers, a pointing to 2 multiples, B pointing to 3 multiples, C pointing to 5 multiples, int a = 0, B = 0, C = 0; / / DP [i] indicates the i+1 ugly number, int[] dp = new int[n]; / / initialization dp:dp[0]=1, the first ugly number is 1, DP [0] = 1; for (int i = 1; I < n; I + +) {/ / formula: DP [i] = min {DP [A-1] * 2, DP [B-1] * 3, DP [C-1] * 5} int N1 = DP [a] * 2; int n2 = dp[b] * 3; int n3 = dp[c] * 5; dp[i] = Math. min(Math.min(n1, n2), n3); // Next, move the pointer / / DP [A-1] * 2 < = DP [i] < DP [a] * 2 if (DP [i] = = N1) {a + +;}// dp[b-1]*3<=dp[i]<dp[b]*3 if (dp[i] == n2) { b++; } // dp[c-1]*5<=dp[i]<dp[c]*5 if (dp[i] == n3) { c++; } } return dp[n - 1]; }}
50 characters that appear only once
Title: find the first character that appears only once in the string s. If not, a single space is returned. S contains only lowercase letters.
Example:
s = "abaccdeff"return "b"s = "" return " "
Limitations:
0 <= s Length of <= 50000
analysis:
- For the number of statistics, you must think of the hash table
- Method 1: hash table < character, number of occurrences >
- Traverse the character array twice, and take the key with value=1 for the second time
- Method 2: hash table < character, Boolean value >, Boolean value is the inverse of the last Boolean value every time, and the rule is as follows:
- 0 occurrences, false
- Appear once, true, traverse the character array twice, and take value=true for the second time
- Appears twice, false
public class Solution {
// Method 1: HashMap < character, integer >
public char firstUniqChar1(String s) {
HashMap<Character, Integer> map = new HashMap<>();
char[] chars = s.toCharArray();
for (char c : chars) {
if (!map.containsKey(c)) {
map.put(c, 1);
} else {
map.put(c, map.get(c) + 1);
}
}
for (char c : chars) {
if (map.get(c) == 1) {
return c;
}
}
return ' ';
}
// Method 2: HashMap < character, Boolean > is much faster than method 1
public char firstUniqChar2(String s) {
HashMap<Character, Boolean> map = new HashMap<>();
char[] chars = s.toCharArray();
for (char c : chars) {
map.put(c, !map.containsKey(c));
}
for (char c : chars) {
// 0 times: false
// 1 time: true. The first time you encounter true, you will return it
// 2 times: false
if (map.get(c)) {
return c;
}
}
return ' ';
}
}
51 reverse order pairs in array
Title: two numbers in the array. If the first number is greater than the next number, the two numbers form an inverse pair. Enter an array and find the total number of reverse pairs in this array.
Example 1:
input: [7,5,6,4]output: 5
analysis:
- In reverse order, the corresponding problem is merging and sorting. Change one line of code of merging and sorting
- In merge sorting, when merging two arrays into one array, the front > back appears. At this time, the difference is the number of pairs in reverse order
public class Solution { // When res is passed as a parameter, various problems will occur. It is easy to define the member variable private int res directly// The principle of merge sort method is to use num [i] > num [J], then the number of pairs in [i,mid] is in reverse order. Public int reversepairs (int [] Num) {int [] temp = New Int [num.length]; res = 0; mergesort (Num, 0, num.length - 1, temp); return res;} private void mergeSort(int[] nums, int l, int r, int[] temp) { if (l >= r) { return; } int mid = l + (r - l) / 2; mergeSort(nums, l, mid, temp); mergeSort(nums, mid+1, r, temp); if (nums[mid] > nums[mid+1]) { merge(nums, l, mid, r, temp); } } private void merge(int[] nums, int l, int mid, int r, int[] temp) { System.arraycopy(nums, l, temp, l, r - l + 1); int p = l, q = mid+1; for (int i = l; i <= r; i++) { if (p > mid) { nums[i] = temp[q++]; } else if (q > r) { nums[i] = temp[p++]; } Else if (temp [P] < = temp [q]) {/ / < = regions will not form reverse pairs, so nums [i] = temp [P + +];} Else {/ / > description must form an inverse pair: [p,mid] and [mid+1,...] Constitute the reverse order pair mid-P + 1, res + = mid - P + 1; nums[i] = temp[q++]; } } }}
Merge sort
public class MergeSort{
private MergeSort() {
}
public static void mergeSort(int[] arr) {
// The temporary array is created at the beginning, passed to the merge, and the arr is copied to the temp array
int[] temp = new int[arr.length];
mergeSort(arr, 0, arr.length - 1, temp);
}
private static void mergeSort(int[] arr, int l, int r, int[] temp) {
if (l >= r) {
return;
}
// Recursion first, partition area
int mid = l + (r - l) / 2;
mergeSort(arr, l, mid, temp);
mergeSort(arr, mid + 1, r, temp);
// Merge again, mid > the previous number is merged
if (arr[mid] > arr[mid + 1]) {
merge(arr, l, mid, r, temp);
}
}
private static void merge(int[] arr, int l, int mid, int r, int[] temp) {
System.arraycopy(arr, l, temp, l, r - l + 1);
int p = l, q = mid + 1;
for (int i = l; i <= r; i++) {
// First, judge whether the two pointers are out of bounds
if (p > mid) {
arr[i] = temp[q++];
} else if (q > r) {
arr[i] = temp[p++];
} else if (temp[p] <= temp[q]) {// Generally, compare the values in auxiliary and put them back into arr
arr[i] = temp[p++];
} else {
arr[i] = temp[q++];
}
}
}
}
52 the first common node of two linked lists
Title: enter two linked lists and find their first common node.

be careful:
If two linked lists have no intersection, return null.After returning the results, the two linked lists must still maintain their original structure. It can be assumed that there is no loop in the whole linked list structure. The procedure shall be satisfied as far as possible O(n) Time complexity, and only O(1) Memory.
analysis:
- Define A len to record the linked list difference. cur1 first traverses the linked list A, len+1; cur2 then traverses the linked list B, len-1
- Judge disjoint: the traversal pointer of two linked lists traverses to the end of the linked list. Finally, if it is not equal, it is disjoint
- len takes an absolute value because the difference may be negative
- Cur1 points to the longer header node and cur2 points to the shorter header node. Let cur1 pointing to the longer header node take the len step first
- Move cur1 and cur2 backward until cur1==cur2. At this time, they must intersect. Return to cur1 | cur2
public class Solution { public ListNode getIntersectionNode(ListNode headA, ListNode headB) { if (headA == null || headB == null) { return null; } ListNode cur1 = headA; ListNode cur2 = headB; // Record the difference between the two linked lists int len = 0; while (cur1.next != null) { len++; cur1 = cur1.next; } while (cur2.next != null) { len--; cur2 = cur2.next; } // If the two traversal pointers are not equal at the end, the two linked lists must not intersect if (cur1! = cur2) {return null;}// Cur1 points to the long linked list cur1 = (len > 0? Heada: headb)// Cur2 points to the short linked list cur2 = (cur1 = = heada? Headb: heada)// Len length difference may be negative len = math abs(len); while (len > 0) { cur1 = cur1.next; len--; } while (cur1 != cur2) { cur1 = cur1.next; cur2 = cur2.next; } return cur1; }}
53 find the number 1 in the sorted array
Title: count the number of times a number appears in the sorted array.
Example 1:
input: nums = [5,7,7,8,8,10], target = 8 output: 2
Example 2:
input: nums = [5,7,7,8,8,10], target = 6 output: 0
analysis:
- [5,7,7,8,8,10], the number of occurrences of T = 8 = the subscript of 10 - the subscript of the first 8. Lenovo uses bisection to find the modified version
- Recall the standard writing method of binary search, and modify one line of code to return the subscript of the first element of > target
public class Solution { // Problem: count the number of occurrences in the sorted array / / dichotomy: find the target because the array is ordered, Consider using the dichotomy public int search (int [] num, int target) {/ / [5,7,7,8,8,10], the number of occurrences of t = 8 / / code reuse: the number of times of 8 = the subscript of 10 - the subscript of the first 8. It is found that the binary search code can be reused. Return getrightmargin (Num, target) - getrightmargin (Num, target - 1);}// Return the first number on the right of target. The subscript private int getrightmargin (int [] arr, int target) {int left = 0; int right = arr.length - 1; while (left < = right) {int mid = left + (right - left) / 2; / / experience: in dichotomy, < = is the right boundary if (arr [mid] < = target) { left = mid + 1; } else { right = mid - 1; } } return left; }}
// Standard binary search private int binarysearch (int [] num, int target) {if (Num = = null | num.length = = 0) {return - 1;} int left = 0; int right = nums. length - 1; while (left <= right) { int mid = left + (right - left) / 2; if (nums[mid] < target) { left = mid + 1; } else if (nums[mid] > target) { right = left - 1; } else { return mid; } } return -1;}
53 missing number in 0-n-1
Title: all numbers in an incremental sorting array with length n-1 are unique, and each number is in the range of 0 ~ n-1. Among the N numbers in the range 0 ~ n-1, there is only one number that is not in the array. Please find this number.
Example 1:
input: [0,1,3]output: 2
Example 2:
input: [0,1,2,3,4,5,6,7,9]output: 8
analysis:
- Case 1: array elements and subscripts correspond completely, for example: [0] returns 1, [0,1] returns 2, [0,1,2] returns 3
- Case 2: the correspondence between array elements and subscripts is incomplete, for example: [0,1,3] returns 2
- In the above two cases, you can traverse the array or binary search and rewrite
public class Solution { // Method 1: traverse the array public int missingnumber1 (int [] Num) {for (int i = 0; I < num.length; I + +) {/ / case 1: the array elements correspond to the subscript completely, for example: [0] returns 1, [0,1] returns 2, [0,1,2] returns 3 if (Num [i] = = I & & I = = num.length - 1) {return num.length;}// Case 2: the correspondence between array elements and subscripts is incomplete. For example: [0,1,3] returns 2 if (Num [i]! = I) {return num [i] - 1;}} return -1; } // Method 2: num [i] = = I is changed to binary search. Public int missingnumber2 (int [] Num) {int left = 0; int right = num.length - 1; while (left < = right) {int mid = left + (right - left) / 2; / / num [I] = = I is changed to num [mid] = = mid / / for example: [0,1] find number 1 and return subscript 2; [0,1,3] When looking for the number 1, go to [3] on the right and look for if (Num [mid] = = mid) {left = mid + 1;} Else {/ / num [mid]! = mid, indicating that there are already missing numbers. Go to the left boundary to find right = mid - 1;}}// Return left pointer return left;}}
54 K-th node of binary search tree
Title: given a binary search tree, please find the k-largest node.
Example 1:
input: root = [3,1,4,null,2], k = 1 3 / \ 1 4 \ 2 output: 4
Example 2:
input: root = [5,3,6,2,4,null,null,1], k = 3
5
/ \
3 6
/ \
2 4
/
1
output: 4
Limitations:
1 ≤ k ≤ Number of binary search tree elements
Analysis: when you see the binary search tree, you think that the middle order traversal is an incremental array
- Method 1: in the middle order traversal of the binary search tree, use the list to record the value of each middle order traversal, and the returned size()-k is the largest number k
public class Solution {
// Method 1: the middle order traversal of the binary search tree, store the value with the linked list, and return the size-k element, which is the k-largest element
public int kthLargest(TreeNode root, int k) {
ArrayList<Integer> list = new ArrayList<>();
inOrderByLR(root, list);
// The first largest number - > the size-1 number after sorting
// The kth largest number - > the size-k number after sorting
return list.get(list.size() - k);
}
private void inOrderByLR(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
inOrderByLR(root.left, list);
list.add(root.val);
inOrderByLR(root.right, list);
}
}
- Method 2: traversal of binary search tree in reverse order
- First traverse the right subtree
- k=0, indicating that the k-th largest number has been found, and the next traversal will stop directly
- Otherwise, k-1 indicates that the k-th largest number has not been found. K-1 determines whether this layer is the k-th largest number
- If k equals 0 after k-1, it means that it is the k-th largest number, and the node value can be returned
- Then traverse the left subtree
public class Solution {
// Method 2: traversal of binary search tree in reverse order
private int res;
private int k;
public int kthLargest(TreeNode root, int k) {
this.res = 0;
this.k = k;
inOrderByRL(root);
return res;
}
private void inOrderByRL(TreeNode root) {
if (root == null) {
return;
}
// First traverse the right subtree
inOrderByRL(root.right);
// If the k-th largest number has been found, the next traversal will stop directly
if (k == 0) {
return;
}
// The k-th largest number, k-1, has not been found. Judge whether this layer is the k-th largest number
k--;
if (k == 0) {
res = root.val;
}
// Then traverse the left subtree
inOrderByRL(root.left);
}
}
Depth of 55-I binary tree
Title: enter the root node of a binary tree to find the depth of the tree. The nodes (including root and leaf nodes) passing from root node to leaf node form a path of the tree, and the length of the longest path is the depth of the tree.
For example:
Given a binary tree [3,9,20,null,null,15,7], the return depth is 3
3
/ \
9 20
/ \
15 7
analysis:
- Recursive method:
- Recurse around the current node and return 0 if null is encountered
- If it is not null, it returns the maximum depth of the current left and right children + 1, which is the depth of the binary tree
- Hierarchy traversal:
- Queue: record the nodes of the upper layer. If the initialization root is not empty, join the queue
- Traverse each node in the queue, and use the temp queue to record the non empty child nodes of each node in the queue
- The queue points to temp again, and the height is res+1
- Just return to res
public class Solution { // Method 1: recursive method public int maxdepth (treenode root) {if (root = = null) {return 0;}// Binary tree depth: maximum left and right subtree depth + 1 return math max(maxDepth(root.left), maxDepth(root.right)) + 1; } // Method 2: traverse the hierarchy of binary tree public int maxdepth1 (treenode root) {if (root = = null) {return 0;}// Queue: record the node of the previous layer LinkedList < treenode > queue = new LinkedList < > (); queue. add(root); int res = 0; While (! Queue. Isempty()) {/ / temp records the node LinkedList < treenode > temp = new LinkedList < > (); for (int i = queue. Size(); I > 0; I --) {treenode node = queue. Poll(); if (node. Left! = null) {temp. Add (node. Left);} if (node.right != null) { temp.add(node.right); } } // Queue points to this layer node, queue = temp// Height + 1 res + +;} return res; }}
55-II balanced binary tree
Title: enter the root node of a binary tree to judge whether the tree is a balanced binary tree. If the depth difference between the left and right subtrees of any node in a binary tree is no more than 1, it is a balanced binary tree.
analysis:
- Method 1: define a function process(TreeNode head) to perform subsequent traversal of the tree to obtain all the information of the left and right subtrees
- If the node is null, it means that it crosses the leaf node and returns height 0
- Recursive left subtree to obtain the height information of left subtree; If - 1, return - 1 as a whole
- Recursive right subtree to obtain the height information of right subtree; If - 1, return - 1 as a whole
- Recursive return: math abs(leftHeight - rightHeight) <= 1 ? Math. max(leftHeight, rightHeight) + 1 : -1
public class Solution { public boolean isBalanced(TreeNode root) { return process(root) != -1; } // Height difference between left and right subtrees < = 1, return to the real height; If the height difference between the left and right subtrees is > 1, return - 1 private int process (treenode head) {if (head = = null) {return 0;} int leftHeight = process(head.left); if (leftHeight == -1) { return -1; } int rightHeight = process(head.right); if (rightHeight == -1) { return -1; } return Math. abs(leftHeight - rightHeight) <= 1 ? Math. max(leftHeight, rightHeight) + 1 : -1; }}
FA 2: Zuo Shenshu mentioned a tree dp in the following way:
-
Step 1 of the tree dp routine: analyze the possibility of the answer in the subtree with a node x as the head node, and this analysis considers the possibility from the perspective of the left subtree of X, the right subtree of X and the whole tree of X.
- Possibility 1: if the left subtree of X is not balanced, the tree with X as the head node is unbalanced.
- Possibility 2: if the right subtree of X is not balanced, the tree with X as the head node is unbalanced.
- Possibility 3: if the height difference between the left subtree and the right subtree of X exceeds 1, the tree with X as the head node is unbalanced.
- Possibility 4: if none of the above possibilities are successful, the tree with X as the head node is balanced.
-
Step 2 of tree dp routine: list all required information according to the possibility analysis in step 1. Both the left subtree and the right subtree need to know whether they are balanced and the height.
-
Step 3 of tree dp routine: summarize according to the information in step 2. The definition information is shown in the ReturnType class.
-
Step 4 of tree dp routine: design recursive function. Recursive function is the answer when X is the head node, including the design of recursive base case. By default, all the information of the left tree and right tree can be obtained directly
public class Solution { public boolean isBalanced(TreeNode root) { return process(root).isBalanced; } private ReturnType process(TreeNode head) { if (head == null) { return new ReturnType(true, 0); } // Get the left and right subtrees ReturnType lefttype = process (head. Left); ReturnType rightType = process(head.right); // Overall balance: left subtree balance, right subtree balance, height difference < = 1, Boolean isbalanced = lefttype isBalanced && rightType. isBalanced && Math. abs(leftType.height - rightType.height) <= 1; // Overall height: maximum height of left and right subtrees + 1 int height = math max(leftType.height, rightType.height) + 1; return new ReturnType(isBalanced, height); }}// Tree dp routine: considering the left and right subtrees, define a case class to receive class ReturnType {Boolean isbalanced; int height; ReturnType (Boolean isbalanced, int height) {this.isbalanced = isbalanced; this.height = height;}}
Number of occurrences of numbers in 56-I array I
Title: in an integer array nums, except for two numbers, other numbers appear twice. Please write a program to find these two numbers that only appear once. The time complexity is O(n) and the space complexity is O(1).
Example 1:
Input: nums = [4,1,4,6]Output:[1,6] or [6,1]
Example 2:
Input: nums = [1,2,10,4,1,4,3,3]Output:[2,10] or [10,2]
Limitations:
2 <= nums.length <= 10000
analysis:
- First learn: "except for one number in an array, other numbers appear twice. Find out this number". The fastest way is XOR operation
// Learn first: except for one number, other numbers in an array appear twice. Find the number public int onenumbers (int [] Num) {/ / 0 and any number XOR are any number itself. Int res = 0; for (int num: Num) {res ^ = num;} return res;}
- This topic is "except for two numbers, the other arrays appear twice". If you can divide the array into two sub arrays containing only one number, you can XOR the two sub arrays respectively
- How to get two different numbers: since all but these two numbers appear twice in the array, only the result of res1^res2 remains in the XOR array. According to the XOR definition, the result is the bit of 1, indicating that the two numbers must be different. Therefore, res1^res2 can be operated to obtain the first different bit of 1 from low to high
- The array is divided into two subarrays containing only one number that occurs once. Method: according to the results of two different number XORs, there is at least one 1 with different bits, so find the first different 1 from low to high, and split the array into two subarrays
- Perform XOR operation on these two arrays respectively, and you can actually get res1 and res2
public class Solution {
public int[] singleNumbers(int[] nums) {
int res1 = 0, res2 = 0;
int m = 0, n = 1;
// 1. Traverse the array so that each element is ^, and the elements that appear twice will be offset
// Cycle end: m=res1^res2
for (int num : nums) {
m ^= num;
}
// 2. Find out the first binary number with different res1 and res2 to group
while ((m & n) == 0) {
n <<= 1;
}
// 3. Divide the array into two groups according to the first binary number different from res1 and res2, and perform ^ operation respectively
for (int num : nums) {
// 4. Each group performs XOR separately
if ((num & n) == 0) {
res1 ^= num;
} else {
res2 ^= num;
}
}
return new int[]{res1, res2};
}
}
Number of occurrences of numbers in 56-II array II
Title: in an array nums, except that one number appears only once, other numbers appear three times. Please find the number that appears only once.
Example 1:
Input: nums = [3,4,3,3] Output: 4
Example 2:
Input: nums = [9,1,7,9,7,9,7] Output: 1
Limitations:
1 <= nums.length <= 10000 1 <= nums[i] < 2^31
analysis:
- Method 1:
- Hash table < character, occurrence times >, if kay already exists, value is set to - 1; Otherwise, 1
- Traverse the hash table and take out the key with value=1
public class Solution {
// Method 1: if you don't make up your mind, find your father
public int singleNumber1(int[] nums) {
HashMap<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
if (!map.containsKey(num)) {
map.put(num, 1);
} else {
// Those already included are marked as - 1, reducing the get operation
map.put(num, -1);
}
}
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
if (entry.getValue() == 1) {
return entry.getKey();
}
}
return -1;
}
}
-
Method 2: finite state automata, learn if you can, and recite formulas if you don't
-
Clear concept: 3 times in [3,3,3,5] and 1 time in 5.
- For numbers that appear three times, the number of occurrences of each binary bit is a multiple of 3
- Count the number of 1 on each binary of each number, and then take the remainder of 3. The remaining binary bits are converted to decimal = the number that appears once
- There are only three states for 3 remainder: 0,1,2. Expressed in binary as 00,01,10
-
The two bits are recorded as two bits and one bit. If a binary bit n, one position is encountered:
-
one: one = one ^ n & ~two
two = 0
n = 0,one = one ==> one = one ^ 0
n = 1,one = ~one ==> one = one ^ 1
two = 1
n = 0/1,one = 0 ==> one = ~two
-
Two position: observe the situation that one position has not changed or has changed. We exchange two and one positions and observe again. It is found that they are the same as one
-
two: two = two ^ n & ~one
-
Traverse the array, ones = ones ^ num & ~ twos and twos = twos ^ num & ~ ones;,
- In each traversal, ones records the number of occurrences for the first time. If the number of occurrences occurs three times, twos and ones will become 0 again, so that the elements that occur three times "offset"
-
After traversal, all that is left is a 1-digit number. Just return ones
public class Solution {
// Method 2: finite state automata
public int singleNumber2(int[] nums) {
int ones = 0;
int twos = 0;
for (int num : nums) {
ones = ones ^ num & ~twos;
twos = twos ^ num & ~ones;
}
return ones;
}
}
57-I and two numbers of s
Title: enter an incrementally sorted array and a number s, and find two numbers in the array so that their sum is exactly s. If the sum of multiple pairs of numbers is equal to s, any pair can be output.
Example 1:
Input: nums = [2,7,11,15], target = 9 Output:[2,7] perhaps [7,2]
Example 2:
Input: nums = [10,26,30,31,47,60], target = 40 Output:[10,30] perhaps [30,10]
analysis:
- The array is incrementally ordered. To find two numbers whose sum is s, we regard s as a target + array order = binary search
- Define two leading and trailing pointers. Pay attention to the traversal condition while (left < right), because two numbers are returned, and left=right directly stops the loop
- As like as two peas, target:target = nums[left] + nums[right], the rest is exactly the same as the standard two point search.
public class Solution { public int[] twoSum(int[] nums, int target) { int left = 0, right = nums.length - 1; while (left < right) { int sum = nums[left] + nums[right]; if (sum < target) { // The array is ordered. When sum < T, it indicates that num [left] is not large enough, and all the right to match the current left cannot be constructed into t left + +;} else if (sum > target) { right--; } else { return new int[]{nums[left], nums[right]}; } } return new int[]{}; }}
Continuous positive sequence with 57-II and s
Title: enter a positive integer target, and output a sequence of continuous positive integers with a sum of target (containing at least two numbers). The numbers in the sequence are arranged from small to large, and different sequences are arranged from small to large according to the first number.
Example 1:
Input: target = 9 Output:[[2,3,4],[4,5]]
Example 2:
Input: target = 15 Output:[[1,2,3,4,5],[4,5,6],[7,8]]
analysis:
- Initialization: i = 1, j = 2, sum = 3, i represents the number of left boundaries, J represents the number of right boundaries, and sum represents the sum of the numbers of this boundary
- First define the result linked list res, and finally grab and replace it with a two-dimensional array
- Cycle end condition: i==j ends, because the boundary needs at least 2 numbers
- Record whether the window value is equal to target first
- Equal to, generate an array of interval lengths, assign values in turn, and store them in the result linked list
- Then move the pointer and window
- Sum > target and sum = target have the same logic, sum -= i++
- sum < target,sum += ++j
- Return: res.toArray(new int[0] [])
public class Solution { public int[][] findContinuousSequence(int target) { // Initialization: I left number, initial test is 1;j is the number on the right, which is initially converted to 2; Therefore, the initialization sum is 3, int i = 1, j = 2, sum = 3// I don't know how large the result array is. Temporarily use the linked list to store the result list < int [] > res = new ArrayList < > ()// End of cycle: the number of left and right boundaries is equal, Jump out of the loop while (I < J) {/ / when equal, record the result to the temporary one-dimensional array, and finally add it to the res linked list if (sum = = target) {int [] temp = New Int [J - I + 1]; for (int k = I; K < = J; K + +) {temp [K - I] = k;} res.add(temp); } // Move the window and pointer, > and = have the same logic, and merge them together to write if (sum > = target) {sum - = I + +;} else { sum += ++j; } } // Variable number of two-dimensional array columns in Java return res.toArray(new int[0] []);}}
58-I reverse word order
Title: input an English sentence and flip the order of words in the sentence, but the order of characters in the word remains the same. For simplicity, punctuation is treated like ordinary letters. For example, if you enter the string "I am a student.", you will output "student. a am I".
Example 1:
input: "the sky is blue"output: "blue is sky the"
Example 2:
input: " hello world! "output: "world! hello"explain: The input string can contain extra spaces before or after, but the inverted characters cannot be included.
Example 3:
input: "a good example"output: "example good a"explain: If there is extra space between two words, reduce the space between words after inversion to only one.
explain:
Characters without spaces form a word. The input string can contain extra spaces before or after, but the inverted characters cannot be included. If there is extra space between two words, reduce the space between words after inversion to only one.
public class Solution {
// Double finger needling, traversing strings in reverse order
public String reverseWords(String s) {
// Remove the leading and trailing spaces
String trim = s.trim();
int last = trim.length() - 1;
// Traversal in reverse order. The traversal pointer initialization points to the end of the array
int index = last;
StringBuilder sb = new StringBuilder();
while (index >= 0) {
// Find the first space character, and its next digit is the last word
while (index >= 0 && trim.charAt(index) != ' ') {
index--;
}
// Add this word to the result string
sb.append(trim, index + 1, last + 1).append(" ");
// Skip the space between adjacent characters to the end of the next word
while (index >= 0 && trim.charAt(index) == ' ') {
index--;
}
// The end pointer points to the end of the word
last = index;
}
// Remove the spaces at the beginning and end of the return result
return sb.toString().trim();
}
}
58-II left rotation string
Title: the left rotation operation of a string is to transfer several characters in front of the string to the end of the string. Please define a function to realize the function of string left rotation operation. For example, if you enter the string "abcdefg" and the number 2, the function will return the result "cdefgab" obtained by rotating two bits left.
Example 1:
input: s = "abcdefg", k = 2 output: "cdefgab"
Example 2:
input: s = "lrloseumgh", k = 6 output: "umghlrlose"
Limitations:
1 <= k < s.length <= 10000
analysis:
- Method 1:
- Use substring() + sb api of append(): sb append(s.substring(n))
- Method 2:
- How to traverse once, add [n,len-1] traversal to the result character, and then add [0,n-1] to the result character
- Answer: start with index =n and calculate i%len
public class Solution { // Method 1: use String library function substring() public String reverseleftwords1 (String s, int n) {StringBuilder sb = new stringbuilder(); sb.append (s.substring (n)); / / [n, s.len] sb.append (s, 0, n); / / [0, n] return sb. Tostring();}// Method 2: public String reverseleftwords2 (String s, int n) {int len = s.length(); StringBuilder sb = new stringbuilder(); / / original s:[0,n-1,n,...,len-1] / / new sb: [n,..., len-1, len,..., N + len-1] for (int I = n; I < n + len; I + +) {sb.append (s.charat (I% len));} return sb. toString(); }}
59-I sliding window maximum
Title: given an array num and the size k of the sliding window, please find the maximum value in all sliding windows.
Example:
input: nums = [1,3,-1,-3,5,3,6,7], and k = 3 output: [3,3,5,5,6,7] explain: Position of sliding window Maximum--------------- -----[1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
Tips:
You can assume k Always valid. When the input array is not empty, 1 ≤ k ≤ Enter the size of the array.
analysis:
- Define a double ended queue to store the array subscript, and the queue head to store the maximum subscript within the range of k, and start traversing the original array
- Pop up at the end of the queue: if the corresponding element of the subscript at the end of the queue > = is brought in, the end of the queue pops up
- Team head pop-up: if the team head coordinates reach i-k, the team head subscript expires and the team head pops up
- Record the maximum value: when the traversal pointer reaches k-1, the maximum value shall be recorded once for each traversal
public class Solution { public int[] maxSlidingWindow(int[] nums, int k) { if (nums == null || nums.length < k || k < 1) { return new int[]{}; } // Double ended queue: [queue head,..., queue tail], storage interval subscript LinkedList < integer > dequeue = new LinkedList < > ()// Number of sliding windows: nums length - k + 1 int[] res = new int[nums.length - k + 1]; int index = 0; // Traverse the original array for (int i = 0; I < num.length; I + +) {/ / queue header: save the maximum value / / currently added elements > = tail elements, tail elements out of queue while (! Dequeue. Isempty() & & num [i] > = num [dequeue. Peeklast()]) {dequeue. Polllast();} dequeue. addLast(i); // Queue head pop-up: if the coordinates of the queue head reach i-k, the queue head element will expire, and the queue head if (dequeue. Peekfirst() = = I - K) {dequeue. Pollfirst();}// Record the maximum value of the window: starting from the k-1 subscript, record the maximum value once in each traversal into the result array if (I > = k - 1) {res [index + +] = num [dequeue. Peekfirst()];}} return res; }}
59-II queue maximum
Title: please define a queue and implement the function max_value gets the maximum value in the queue and requires the function max_value,push_back and pop_ The average sharing time complexity of front is O(1).
If the queue is empty, pop_front and max_value needs to return - 1
Example 1:
input: ["MaxQueue","push_back","push_back","max_value","pop_front","max_value"][[],[1],[2],[],[],[]]output: [null,null,null,2,1,2]
Example 2:
input: ["MaxQueue","pop_front","max_value"][[],[],[]]output: [null,-1,-1]
analysis:
- Two queues are defined: queue performs normal operations; deque save Max
- push_back: in order to ensure that the average sharing time complexity is O(1), the maximum value is stored in the head of the double ended queue. The elements to be added > = / > the tail elements, and all the tail elements will be out of the queue
- pop_front: if the out of queue element is the maximum value element, the deque queue should also be out of the queue head element; Otherwise, the queue header element is sufficient
- max_value: just get the deque team head element
public class MaxQueue { // Ordinary queues ensure push, pop private queue < integer > queue// The double ended queue maintains monotonicity: the newly added element < = the tail of the queue element private deque < integer > deque; public MaxQueue() { queue = new LinkedList<>(); deque = new LinkedList<>(); } public void push_ Back (int value) {/ / add the element > the end of the double ended queue first. When the double ended queue goes out of the queue, find the first element of < = while (! Deque. Isempty() & & value > deque. Peeklast()) {deque. Polllast();}// Double ended queue: only the largest deque is stored in the header offerLast(value); queue. offer(value); } public int pop_ front() { if (queue.isEmpty()) { return -1; } int value = queue. poll(); if (value == max_value()) { deque.pollFirst(); } return value; } public int max_ Value() {if (deque. Isempty()) {/ / condition: Max stack is empty, return - 1;} return deque. peekFirst(); } }
60 n dice points
Title: throw n dice on the ground. The sum of points on the upward side of all dice is s. Enter n to print out the probability of occurrence of all possible values of S. You need to use an array of floating-point numbers to return the answer, in which the i-th element represents the probability of the i-th smallest in the set of points that the N dice can roll.
Example 1:
input: 1 output: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]
Example 2:
input: 2 output: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
1 <= n <= 11
analysis:
- In order to reduce the time complexity, two one bit arrays are defined: dp and next arrays
- dp array: save the number of points and probability of the ith sieve, initialize 6 sizes, and initialize element probability of 1.0 / 6.0
- Next: record the next round of dp array, and finally let dp point to next
- Clear concept: the points and total number of the nth Dice: 5*n+1, because one dice: 6 points and; 2 Dice: 6 + 5 points and
- Initialize the first dice: the number of points and the total number are 6, and the probability is 1.0 / 6.0
- Calculate the number and probability of dice 2 to n
- Each round generates the next array of points and total length of the theory
- Traverse the dp array of the previous round, and traverse the next array of this round every 6 numbers
- The previous round of dp[j] has an impact of dp[j]/6.0 on every 6 numbers after it
- The dp of this round points to the next round
- Return to: dp
public class Solution { public double[] dicesProbability(int n) { // Initialize the first dice: the number of points and the total number are 6, and the probability is 1.0 / 6.0 double [] DP = new double [6]; Arrays. fill(dp, 1.0 / 6.0); // Calculate the number and probability of dice 2 to n for (int i = 2; I < = n; I + +) {/ / 1 Dice: 6 points and; 2 Dice: 6 + 5 points and / / N Dice: 6+(n-1)*5=5n+1 points and double[] next = new double[5 * i + 1]; / / traverse the DP array for (int j = 0; J < DP. Length; j + +) of the previous round {/ / every six numbers, traverse the next array for (int k = 0; K < 6; K + +) {/ / the previous round of dp[j] has an effect of dp[j]/6.0 on every six numbers after it. Next [J + k] + = dp[j]/6.0;}}// The DP array of the previous round is updated to the next array of this round DP = next;} return dp; }}
Shunzi in playing cards
Title: draw 5 cards randomly from playing cards to judge whether it is a surplus, that is, whether the 5 cards are continuous. 2 ~ 10 is the number itself, a is 1, J is 11, Q is 12, K is 13, and DA and Xiao Wang are 0, which can be regarded as any number. A cannot be regarded as 14.
Example 1:
input: [1,2,3,4,5]output: True
Example 2:
input: [0,0,1,2,5]output: True
analysis:
- Efficient judgment is the best way to judge whether it is enough or not:
- Since the king of size is 0, you will skip when you encounter the king of size
- Except for the size king, all numbers cannot be repeated. set is used to store each array element to judge the repetition
- Except for king and king, max min < 5; Because even if there are two size kings, max min will only be smaller
public class Solution { // Draw five cards from a playing card, Judge whether it is a shunzi public Boolean istraight (int [] Num) {/ / set judge whether there is a duplicate number set < integer > set = new HashSet < > (); / / the shunzi size of playing cards ranges from 0,A=1 to K=13, and the range [0,13] int min = 13, max = 0. / / traverse each number in the array for (int num: Num) {/ / if it is the king of size, skip if (Num = = 0) {continue;} Else {/ / is not the king of size, / / if there are repeated numbers, it is impossible to form a shunzi if (set. Contains (Num)) {return false;} Else {/ / if there are no repeated numbers, find the current max,min / / each round must meet the conditions for judging shunzi: max min < 5 min = math.min (min, Num); max = math.max (max, Num) ; // Put the current element into the set to pave the way for subsequent traversal of repeated elements add(num); } } } // Returns the Boolean value of max min < 5 in the entire array. Return max - min < 5;}}
62 the last remaining number in the circle
Title: the N numbers 0,1, ···, n-1 are arranged in a circle, starting from the number 0, and the m-th number is deleted from the circle each time (counting from the next number after deletion). Find the last number left in the circle.
For example, the five numbers 0, 1, 2, 3 and 4 form a circle. Starting from the number 0, delete the third number each time, then the first four deleted numbers are 2, 0, 4 and 1 in turn, so the last remaining number is 3.
Example 1:
input: n = 5, m = 3 output: 3
Example 2:
input: n = 10, m = 17 output: 2
Limitations:
1 <= n <= 10^5 1 <= m <= 10^6
analysis:
- Derivation of Joseph loop problem:
- The array is [0,n-1]. Delete the m-th number, which corresponds to the number of M-1 subscripts deleted. Because it is a cycle, it is the number of (m-1)%n subscripts deleted, and the remaining m%n subscripts are recalculated
- After one round of deletion, start counting again from the elements with t=m%n subscript, then the t position is the first number left after the previous round of deletion of t-1 position, that is, the solution to the f(n) problem!!
- Let n=5, m=3, and the last remaining number is 3
- [n,m] problem: [0,1,2,3,4], do not care about this layer, but how to get the solution from the upper layer
- [n-1,m] problem: [0,1,2,3]. Suppose we know that the solution of [n-1,m] is the number 0 (to align with the 0 subscript of the initial array), then the solution of [n,m] is (0+m)% n = (0+3)%5=3
- Recurrence formula: f(n, m) = [f(n-1, m) + M]% N, and specify f(1,m) =0
public class Solution {
// Dynamic programming: the most understandable version
public int lastRemaining1(int n, int m) {
int[] dp = new int[n];
// The solution of f(1,m) is always 0
dp[0] = 0;
for (int i = 1; i < n; i++) {
// Dynamic transfer equation: f(n,m)=[f(n-1,m)+m]%n
// Note: when dp[i], the array length is i+1
dp[i] = (dp[i - 1] + m) % (i + 1);
}
return dp[n - 1];
}
// Dynamic programming: no need to open up dp array
public int lastRemaining2(int n, int m) {
// N represents the length of the array. When n = length 1, res=0
int res = 0;
for (int i = 2; i <= n; i++) {
// res = (res +m) % n
res = (res + m) % i;
}
return res;
}
}
63 maximum profit of shares
Title: suppose the price of a stock is stored in the array in chronological order, what is the maximum profit that can be obtained from buying and selling the stock at one time?
Example 1:
input: [7,1,5,3,6,4]output: 5 explain: On day 2 (stock price) = 1)When buying, on day 5 (stock price) = 6)When you sell, you make the most profit = 6-1 = 5 . Note that the profit cannot be 7-1 = 6, Because the selling price needs to be greater than the buying price.
Example 2:
input: [7,6,4,3,1]output: 0 explain: under these circumstances, No transaction completed, So the maximum profit is 0.
analysis:
-
[7,1,5,3,6,4] represents the stock price. Each number can be buy / sell (only one purchase and one sale can be made), and the selling price needs to be greater than the buying price
-
Formula derivation:
- Maximum profit = max (previous maximum profit, today's profit)
- The previous maximum profit, initialization: dp[0]=0, because there is no profit on the first day
- Today's profit = today's price - previous lowest price
-
Dynamic planning:
- Definition dp[i]: represents the maximum profit from day 1 to day i+1, = the maximum profit before prices[i]
- minPrice variable: record the minimum price from day 1 to day i+1
-
Dynamic transfer: dp[i]= max(dp[i-1],prices[i]-minPrices(i))
-
Return value: dp[len-1]
public class Solution {
// Dynamic programming: the easiest way to understand
public int maxProfit1(int[] prices) {
if (prices.length == 0) {
return 0;
}
int n = prices.length;
// dp[i]: indicates the maximum profit of the array with prices[i] as the end
int[] dp = new int[n];
// The profit on the first day is 0, because one day can only buy but not sell
dp[0] = 0;
int minPrice = prices[0];
for (int i = 1; i < n; i++) {
// Calculate the minimum price of [0,i]
minPrice = Math.min(minPrice, prices[i]);
// DP [i] = max (maximum profit since the previous day, maximum profit on day I)
dp[i] = Math.max(dp[i - 1], prices[i] - minPrice);
}
return dp[n - 1];
}
// Dynamic programming: simplified writing, not recommended
public int maxProfit2(int[] prices) {
if (prices.length == 0) {
return 0;
}
int maxProfit = 0;
int minPrice = prices[0];
for (int i = 1; i < prices.length; i++) {
minPrice = Math.min(minPrice, prices[i]);
maxProfit = Math.max(maxProfit, prices[i] - minPrice);
}
return maxProfit;
}
}
64 find 1 + 2 + 3 +... + n
Title: for 1 + 2 +... + n, it is required that keywords such as multiplication and division, for, while, if, else, switch, case and conditional judgment statements (A?B:C) cannot be used.
Example 1:
input: n = 3 output: 6
Example 2:
input: n = 9 output: 45
Limitations:
1 <= n <= 10000
analysis:
- First learn sumN(), understand the common recursive writing method of summation function
private int sumN(int n) { // Stop recursion when n=1 if (n = = 1) {return 1;}// n> 1, start recursion / / sum = n + fun (n-1) = n + n-1 + fun (n-2) n += sumN(n - 1); return n;}
- If you can't use conditional sentences such as multiplication, division and judgment, use & & to complete the judgment
- Modify sumN() to complete recursion by using the short circuit effect of logic and:
- Short circuit utility: if the former condition is not satisfied, the latter condition will not be executed. It is thought that the recursive end condition n=1 is changed to & & the former condition is n > 1
- Special note: Java & & syntax considerations
- boolean x =..., Because a & & B needs a return value to accept as a whole, otherwise an error will be reported if it is returned separately
- A & & B, both sides need Boolean values. It is easy to think of N > 1 in a, and > 0 in B uses 1 ++ n> 0 to round up Boolean values
public class Solution { // Multiplication and division, for, while, if, else, switch Keywords such as case and conditional judgment statement public int sumnums (int n) {/ / recursion starts when n > 1. If you can't use conditional judgment statements, use & & to complete the judgment. / / Boolean x =..., a & & B needs a return value to accept as a whole, otherwise an error will be reported if returned separately. / / A & & B, Boolean values are required on both sides. It's easy to think of N > 1 of A. for > 0 in B, use 1 +... + n > 0 to round up the Boolean value Boolean x = (n > 1) & & (n + = sumnums (n - 1) ) > 0; // Return n return n;}}
65 addition without addition, subtraction, multiplication and division
Title: write a function and find the sum of two integers. It is required that four operation symbols "+", "-", "*", "/" shall not be used in the function body.
Example:
input: a = 1, b = 1 output: 2
Tips:
a, b Both may be negative or 0, and the result will not overflow a 32-bit integer
analysis:
- Observe the binary addition of 0 and 0, 0 and 1, 1 and 0, 1 and 1, the result of no carry sum = XOR, and the result of carry value = and
- Derivation: a + b = carry of a and b + no carry sum of a and b
public class Solution { // Method 1: iterative method, Public int ADD1 (int a, int b) {/ / sum saves no carry and int sum = 0. / / b saves the carry result. / / when carry b=0, stop the loop while (b! = 0) {/ / A + B = carry of a and B + carry free sum of a and B / / carry free sum of a and B = the same value of a & & B / / carry free sum of a and B = the same value of a^b sum = a^b; b = (a & B) < < 1; a = sum;} return a; } // Method 2: recursive method public int add2 (int a, int b) {/ / when b=0, a if (b = = 0) {return a;}// A + B = carry of a and B + no carry sum of a and B, which can be directly modified to recursive return add2 (a^b, (A & B) < < 1);}}
66 building a product array
Title: given an array A[0,1,..., n-1], please construct an array B[0,1,..., n-1], where the value of B[i] is the product of elements in array a other than subscript i, that is, B[i]=A[0] × A[1] ×…× A[i-1] × A[i+1] ×…× A[n-1]. Division cannot be used.
Example:
input: [1,2,3,4,5]output: [120,60,40,30,24]
Tips:
The sum of all element products does not overflow a 32-bit integer a.length <= 100000
analysis:
- If you can't use division, try to use multiplication. The result array is b[i]=A[0] × A[1] ×…× A[i-1] × one × A[i+1] ×…× A[n-1], with b[i] position as 1, a two-dimensional array with main diagonal of 1 can be constructed. The main diagonal divides I position into upper and lower triangles. It can be clearly seen that b[i] = upper triangle × Lower triangle
- First calculate the product of the lower triangle: b[i] = b[i - 1] * a[i - 1]
- Then calculate the product of the upper triangle: use the temp temporary variable to record the product of the upper triangle, and then multiply by b[i]
public class Solution {
// You cannot use division to build a product array
public int[] constructArr(int[] a) {
if (a.length == 0) {
return new int[]{};
}
int n = a.length;
// The first for:b[i] represents the product of all numbers of a[0...i-1]
// The second for:b[i] represents the product of all numbers of a[0...i-1,i+1,...n-1]
int[] b = new int[n];
b[0] = 1;
int temp = 1;
// Calculate the product of the lower triangle
for (int i = 1; i < n; i++) {
// Product of all numbers of a[0...i-1]: the number traversed in the previous round of b[i-1]*a
b[i] = b[i - 1] * a[i - 1];
}
// End of the lower triangle of the previous round of calculation: the result of b[len-1] has been determined
// Start traversing back from n-2 and calculate the product of the upper triangle
for (int i = n - 2; i >= 0; i--) {
// temp is the result of multiplying the number after i
temp *= a[i + 1];
// b[i] overall = upper triangle * lower triangle
b[i] *= temp;
}
return b;
}
}
67 convert string to integer
Title: write a function StrToInt to convert a string into an integer. atoi or other similar library functions cannot be used.
-
First, the function discards useless opening space characters as needed until the first non space character is found.
-
When the first non empty character we find is a positive or negative sign, we combine the symbol with as many consecutive numbers as possible as the sign of the integer; If the first non null character is a number, it is directly combined with subsequent consecutive numeric characters to form an integer.
-
In addition to the valid integer part of the string, there may also be redundant characters. These characters can be ignored and should not affect the function.
-
Note: if the first non whitespace character in the string is not a valid integer character, the string is empty, or the string contains only whitespace characters, your function does not need to convert.
-
In any case, if the function cannot perform a valid conversion, return 0.
explain:
Assuming that our environment can only store 32-bit signed integers, the range of values is [− 231, 231 − 1]. If the value exceeds this range, return INT_MAX (231 − 1) or INT_MIN (−231) .
Example 1:
input: "42"output: 42
Example 2:
input: " -42"output: -42 explain: The first non white space character is '-', It's a minus sign. We try to combine the minus sign with all the subsequent consecutive numbers to get the final result -42 .
Example 3:
input: "4193 with words"output: 4193 explain: Conversion to number '3' ,Because its next character is not a number.
Example 4:
input: "words and 987"output: 0 explain: The first non null character is 'w', But it is not a number or a plus or minus sign. Therefore, a valid conversion cannot be performed.
Example 5:
input: "-91283472332"output: -2147483648 explain: number "-91283472332" Exceeds the range of 32-bit signed integers. So return INT_MIN (−231) .
analysis:
- Strings that can be converted normally are divided into integer types: leading and trailing spaces + sign bits + strings spliced with numbers + non numeric departments
- The digital part is the difficulty. num receives the string spliced by the digital part, which will cross the boundary in two cases:
- Num > int max. / 10
- Num = the maximum value of int and the number currently spliced is 7 (because the single digit number of the maximum value of int type is 7)
- In case of out of bounds, the maximum value of the current symbol bit is returned directly
- No out of bounds, number part: num = num * 10 + the number represented by the current character
public class Solution { public int strToInt(String str) { // Remove the leading and trailing spaces: the original array is converted into a character array char [] C = str.trim() toCharArray(); if (c.length == 0) { return 0; } // The initial test res and the maximum value / 10 are used as the boundaries of each product of res, boundary int num = 0, maxboundary = integer MAX_ VALUE / 10; // Index: numeric index, initialized to 1 / / sign: negative sign, 1 positive sign, - 1 negative sign, int index = 1, sign = 1// In the first part, there are three situations: + / / / number / / +: initialize to 1 if (C [0] = '-') {/ / -: when a negative sign is encountered, sign becomes - 1 sign = - 1;} Else if (C [0]! = '+') {/ / non numbers are left, initialization pointer = 0, index = 0;}// Index traverses the string array for (int i = index; I < c.length; I + +) {/ / if a non numeric part is encountered, stop the loop if (C [i] < '0' | C [i] > '9') {break;}// Two cases of num out of bounds: the maximum value of int type is 2147483647217483647, the last number is 7, and the boundary / / 1 after / 10 Num = maximum value / 10 and C [i] > '7', the product must cross the boundary / / 2 If (Num > maxboundary | num = = maxboundary & & C [i] > '7') {return sign = = 1? Integer.max_value: integer.min_value;}// Splicing digital part num = num * 10 + (c[i] - '0');}// Return sign * number return sign * num;}}
Nearest common ancestor of 68-I binary search tree
Title: given a binary search tree, find the nearest common ancestor of two specified nodes in the tree.
Baidu Encyclopedia defines the nearest public ancestor as: "for two nodes p and q with root tree T, the nearest public ancestor is expressed as a node x, which satisfies that x is the ancestor of p and q, and the depth of X is as large as possible (a node can also be its own ancestor)."

analysis:
- Conditions: 1 Binary search tree to ensure that the left is small and the right is large; 2. Node values are not repeated; 3. P and Q correspond to two different nodes respectively
- Recursive method:
- p. Q left and right, then the nearest common ancestor is root
- p. Q is on the right of root, and the nearest common ancestor is on the right of root
- p. Q is on the left of root, and the nearest common ancestor is on the left of root
- Iterative method:
- Traverse the binary search tree. If P and Q are left and right, then the nearest common ancestor is root. Stop the loop and recurse directly
- p. Q is on the right of root, and root points to its right child
- p. Q is on the left of root, and root points to its left child
public class Solution {
// Method 1: recursive method
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root.val < p.val && root.val < q.val) {
// The current result is recorded for each iteration, so return every time
return lowestCommonAncestor(root.right, p, q);
}
if (root.val > p.val && root.val > q.val) {
return lowestCommonAncestor(root.left, p, q);
}
return root;
}
// Method 2: iterative method
public TreeNode lowestCommonAncestor1(TreeNode root, TreeNode p, TreeNode q) {
while (root != null) {
// p. Q is in the right subtree of root, and the nearest public ancestor must be in the right subtree
if (root.val < p.val && root.val < q.val) {
root = root.right;
} else if (root.val > p.val && root.val > q.val) {
// p. Q is in the left subtree of root, and the nearest common ancestor must be in the left subtree
root = root.left;
} else {
// p. Q is on the left and right sides of root. The nearest common ancestor is root
break;
}
}
return root;
}
// Method 3: optimize method 2 to ensure p.val < q.val and reduce the while judgment conditions
public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) {
// Make sure the left is small and the right is large,
if (p.val > q.val) {
TreeNode temp = p;
p = q;
q = temp;
}
while (root != null) {
// Root is smaller than the smallest, which means that root appears on the left of P and Q, and the common ancestor is on the right of root
if (root.val < p.val) {
root = root.right;
} else if (root.val > q.val) {
// Root is larger than the largest one, which means that root appears on the right of P and Q, and the common ancestor is on the left of root
root = root.left;
} else {
// Root is neither bigger than the largest one in P and Q, nor smaller than the smallest one. The nearest common ancestor is root. Stop the loop
break;
}
}
return root;
}
}
The nearest common ancestor of 68-II binary tree
Title: given a binary tree, find the nearest common ancestor of two specified nodes in the tree.
Baidu Encyclopedia defines the nearest public ancestor as: "for two nodes p and q with root tree T, the nearest public ancestor is expressed as a node x, which satisfies that x is the ancestor of p and q, and the depth of X is as large as possible (a node can also be its own ancestor)."
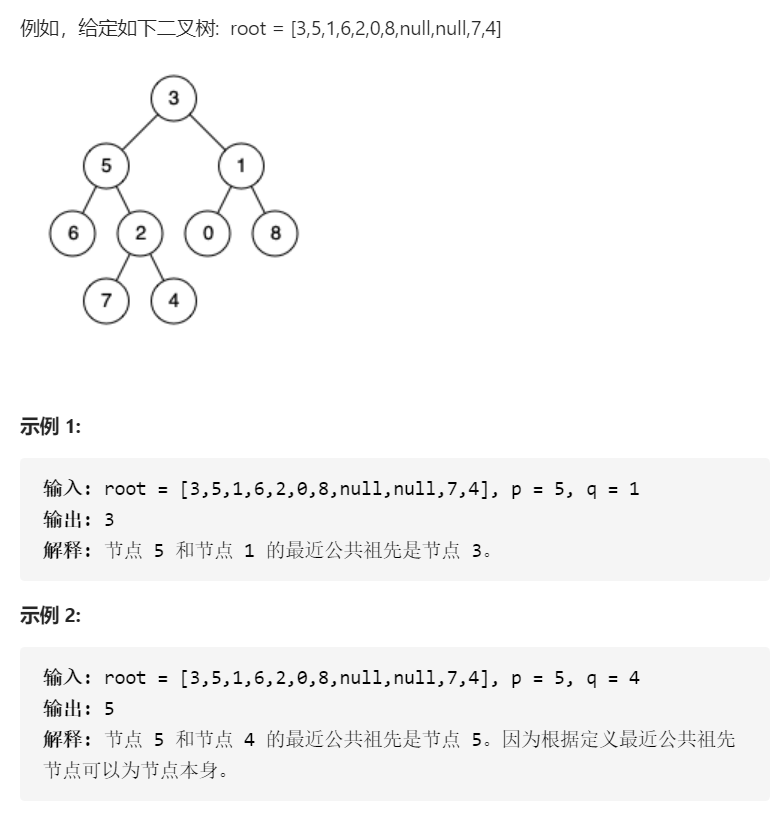
analysis:
- Because the ordinary binary tree has no special properties, but the subsequent traversal can record the information of the left and right child nodes before operation, so the subsequent traversal is used
- Recursion end condition:
- The traversal pointer crosses the leaf node and returns null
- Traversal pointer = p or q, return traversal pointer
- Start recursion:
- Recursive left subtree, received with left
- Recursive right subtree, received with right
- Return value:
- When left and right are not empty at the same time: it means that P and Q are on the opposite side of root, and root is the nearest public ancestor
- When left and right are both empty: it means that the left and right subtrees of root do not contain P and Q, and there is no common ancestor
- When left and right are empty and the other is not empty, the nearest common ancestor must be in the subtree whose root is not empty
public class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// Recursive end condition
// root crosses the leaf node and returns null
// root = p/q, the nearest common ancestor is root itself, and root is returned
if (root == null || root == p || root == q) {
return root;
}
// Set the current node as cur, use post order traversal to record the left and right subtrees of the current node, and use left and right to receive
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
// When left and right are not empty at the same time: it means that P and Q are on the opposite side of root, and root is the nearest public ancestor
if (left != null && right != null) {
return root;
}
// When left and right are both empty: it means that the left and right subtrees of root do not contain P and Q, and there is no common ancestor
// When left and right are empty and the other is not empty, the nearest common ancestor must be in the subtree whose root is not empty
return left != null ? left : right;
}
}