Chapter II linear table

2.1 outline requirements

(1) Basic concepts of linear table
(2) Implementation of linear table
　 1. Sequential storage
　 2. Linked Storage
(3) Application of linear table

2.2 basic concept of linear table

Definition of linear table: a linear table is a finite sequence of elements with the same characteristics
The storage structure of linear list: sequential storage and chain storage, that is, sequential list and chain list,
          definition of sequence table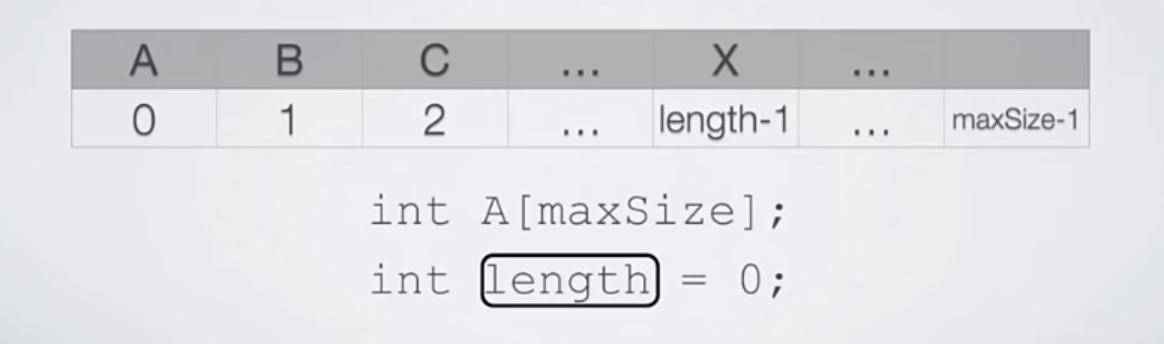
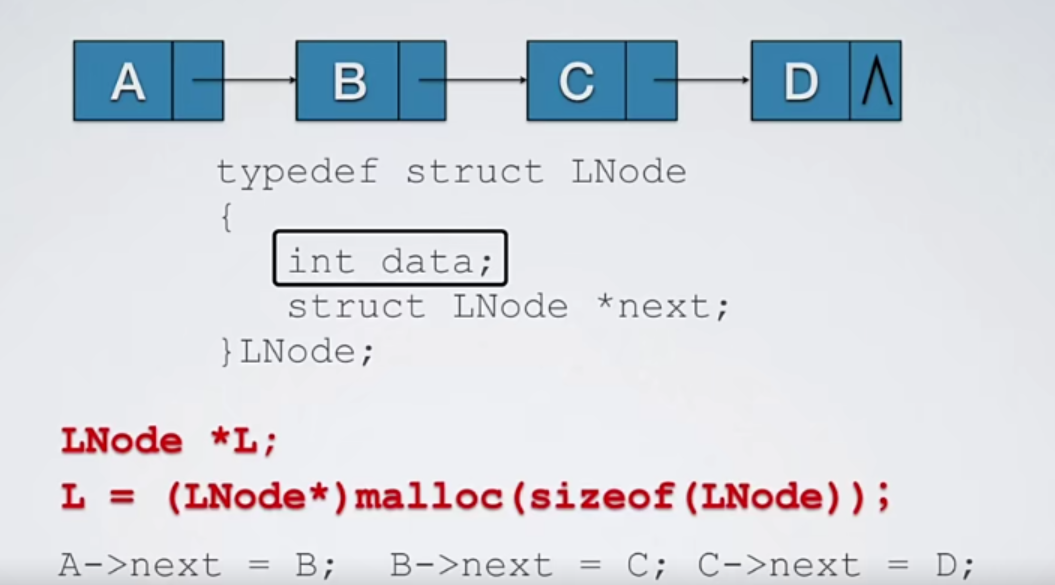
          definition of linked list

storage structure	logically	Physical address
Sequence table	adjacent	adjacent
Linked list	adjacent	Not necessarily adjacent

The Head pointer is used to completely identify the whole linked list

The empty judgment conditions of single linked list are:
Single linked list with header node: Head->next = NULL
 Single linked list without head node: Head = NULL

Double linked list

The difference from the single linked list is that a pointer to the precursor is added to each node.
The empty judgment condition is the same as that of the single linked list.

Circular single linked list

The empty judgment conditions of circular single linked list are:
Circular single linked list with header node: Head->next = Head
 Circular single linked list without leading node: Head = NULL

Circular double linked list:

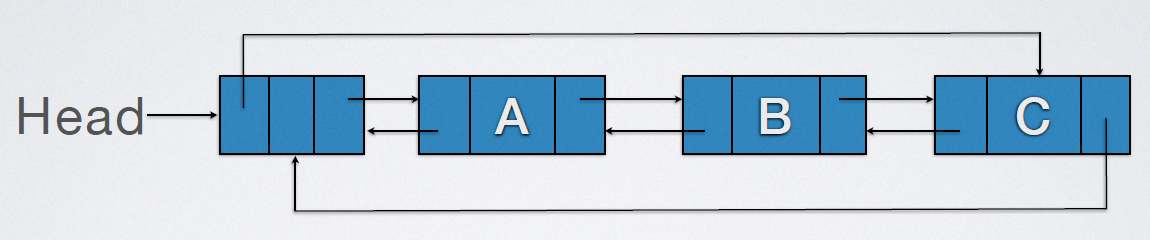
The empty judgment conditions of circular double linked list are:
Header node: Head->next=Head or Head->prior=NULL
 Circular single linked list without leading node: Head = NULL

Exercise 1:

#include<iostream>
#include<cmath>
using namespace std;
#define MIN 0.001
#define MAXSIZE 100
int compare(float A[],int alen,float B[],int blen)
{
    int i = 0;
    while(i < alen && i < blen)
    {
        if (fabs(A[i]-B[i])<MIN)
            ++i;
        else
            break;
    }
    if(i >= alen && i >= blen)
        return 0;
    else if((i>=alen&&i<blen) || A[i]<B[i])
        return -1;
    else
        return 1;
}
int main()
{
    float A[MAXSIZE] = {1,2,3,4};
    float B[MAXSIZE] = {1,2,3,4,5,6};
    cout <<compare(A,4,B,6);
    return 0;
}

2.3 comparison of storage structure characteristics

2.3.1 insert delete element

2.3.1.1 sequence table insertion

When a position is selected, all elements move one position to the right from the back to the front. From front to back will result in element coverage.

2.3.1.2 deletion of sequence table

When the position is selected, all elements from the front to the back move one position to the left in turn. From back to front will result in element coverage.

2.3.1.3 conclusion

The insertion and deletion of sequential list may lead to the joint operation of a large number of elements, while the linked list will not.

2.3.2 element extraction

Finding the location of any node in a single linked list is not as simple as a sequential list, because the sequential list supports random storage, while the linked list does not.

2.3.3 storage space

Linear table adopts sequential storage structure, which must occupy a whole piece of continuous storage space, while chain storage structure does not need this;
From the overall point of view of the table, the storage space utilization of the general sequential table is lower than that of the linked list, but from the perspective of a single storage unit, the utilization of the sequential table is higher than that of the linked list.
Storage density refers to the ratio of the storage occupied by the node itself to the storage occupied by the whole storage structure.
Exercise 2:

Select A because the sequence table supports random storage

Select B, exclusion method

2.4 calculation of element movement times and static linked list

2.4.1 calculation of element movement times

It is mainly used to insert and delete elements in the sequence table.
The insertion position of a sequence table with length n is n+1, so the probability of inserting elements at any position is: 1 n + 1 \frac{1}{n+1} n+11​；
Insert elements before position i, and n-1 elements need to be moved;
So the average number of moves of the inserted element is n 2 \frac{n}{2} 2n​；
The insertion position of a sequence table with length n is n+1, so the probability of deleting elements at any position is: 1 n \frac{1}{n} n1​；
Insert elements before I position, and n-i-1 elements need to be moved;
So the average number of moves of the inserted element is n − 1 2 \frac{n-1}{2} 2n−1​；

2.4.2 static linked list

Static linked list node type definition:

typedef struct
{
	int data;
	int next;
}SLNode;

Construct a static linked list with length MAXSIZE:

SLNode SLink[MAXSIZE];

int p = Ad0; //Define a pointer
SLink[p].data;//Take the node value pointed to by P, which is equivalent to p - > data
SLink[p].next;//Take the subsequent node pointer of P, which is equivalent to p - > next
 stay p Insert node after q: 
SLink[q].next = SLink[p].next;
Slink[p].next = q;
//Analogy q.next = p.next p.next = q

Exercise 3:

Choose B
A. Both are O(1)
C. Linked lists with the same number of nodes occupy the same storage space

Choose C
A. It's not simple
B. Random storage is not supported
D. Can't make good use of scattered storage space

2.5 linear table insertion and deletion

2.5.1 inserting and deleting elements in single linked list

2.5.1.1 insertion

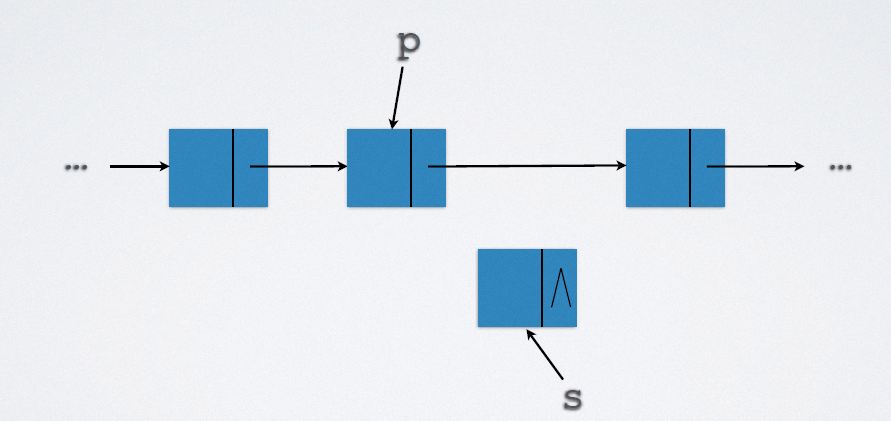
Implementation code:

s->next = p->next;
p->next = s;

2.5.1.2 delete

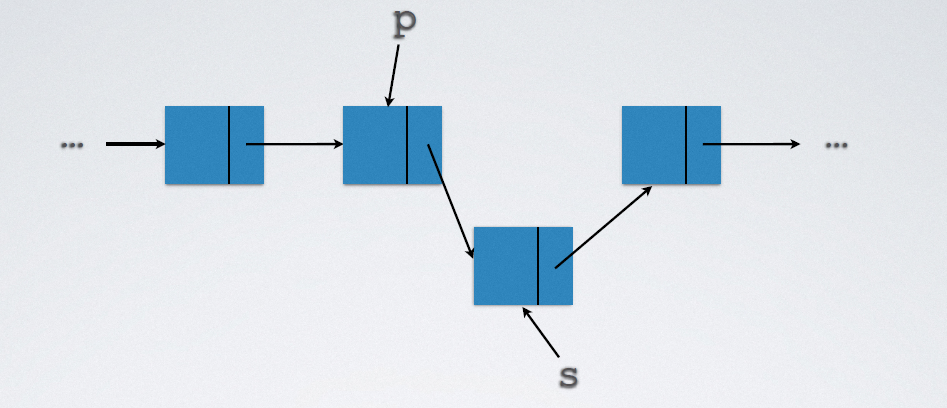
Implementation code:

p->next = s->next;
free(s);

2.5.2 double linked list insert delete element

2.5.2.1 insertion

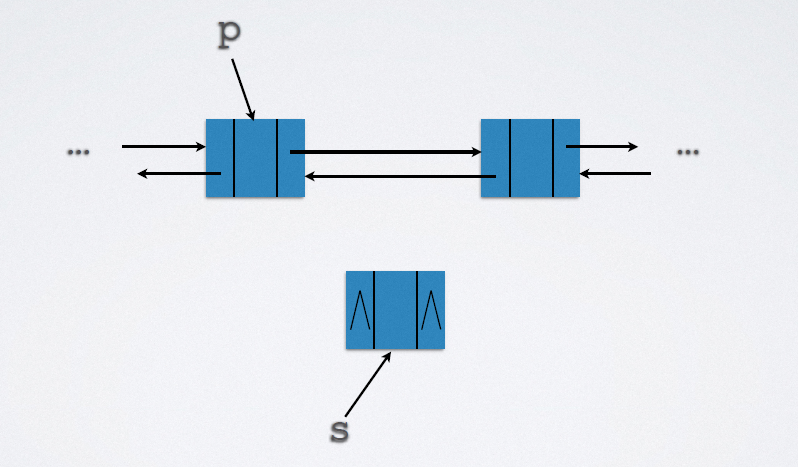
Implementation code:

p->next = s-next;
s->prior = p;
p->next = s;
s->next->prior = s;

2.5.2.2 deletion

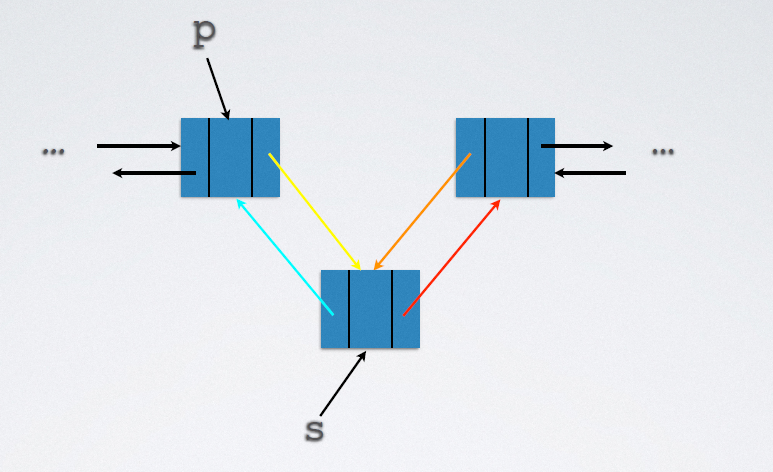
Implementation code:

s->prior->next = s->next 
s->next->prior = s->prior
free(s);

2.5.3 insertion and deletion of sequence table elements

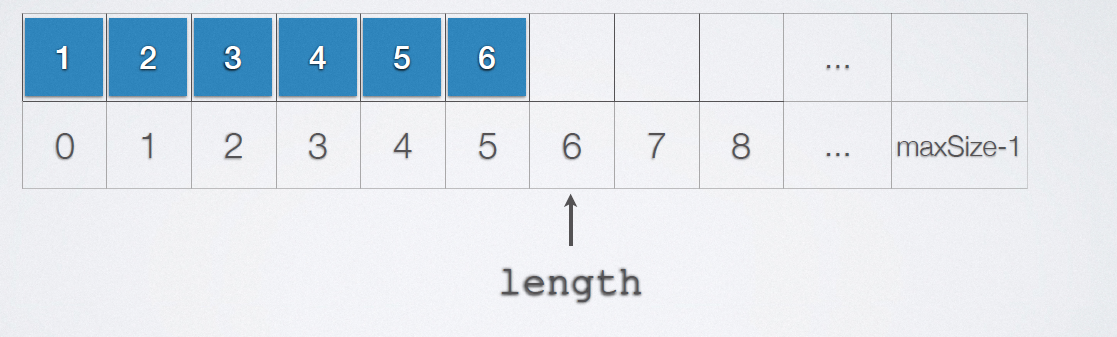
2.5.3.1 insert elements

Position of insertable element: 0-length;
When length=maxsize, no more elements can be inserted;
Move elements from front to back.

Insert operation implementation code:

int sqList[maxsize] = {1,2,3,4,...n};
int length = n;
int InsertElem(int sqList[],int &length,int p,int e)
{
    if(p<0||p>length||length==maxsize)
        return 0;
    for(int i = length-1;i>=p;--i)
    {
        sqList[i+1]=sqList[i];
    }
    sqList[p]=e;
    ++length;
    return 1;
}

2.5.3.2 delete element

Position of insertable element: 0-length-1;
When length=0, no more elements can be inserted;
Move elements from back to front.

Delete operation implementation code:

int sqList[maxsize] = {1,2,3,4,...n};
int length = n;
int DeleteElem(int sqList[],int &length,int p,int e)
{
    if(p<0||p>length-1)
        return 0;
    e = sqList[p];
    for(int i = p;i<length-1;++i)
    {
        sqList[i]=sqList[i+1];
    }
    --length;
    return 1;
}

Exercise 4:

Select B. the longer the linked list, the more data to scan

void DeleteElem(int sqList[],int &length,int p,int e)
{
    int len = j-i+1;
    for(int k = j+1;k<length;++i)
    {
        sqList[k-len]=sqList[k];
    }
    length-=len;
}

void del(LNode *L)
{
	LNode *p = L-next,*q;
	while(p->next !=NULL)
	{
		if(p->data==p->next-data)
		{
			q = p->next;
			p->next = q->next;
			free(q);
		}
		else
		{
			p = p->next;
		}
	}
}

void spilit(LNode *A,LNode *B)
{
	B = (LNode*)molloc(sizeof(LNode));
	LNode *p,*q,*r;
	B->next = NULL;
	r = B;
	p = A;
	while(p->next!=NULL)
	{
		if(p->next->data%2==0)
		{
			q = p->next;
			p->next= q->next;
			q->next =NULL;
			r->next =q;
			r = q;
		}
		else
		{
			p = p->next;
		}
	}
}

2.6 table building

2.6.1 construction of sequence table

Implementation code:

2.6.2 linked list creation

Implementation code (tail interpolation):

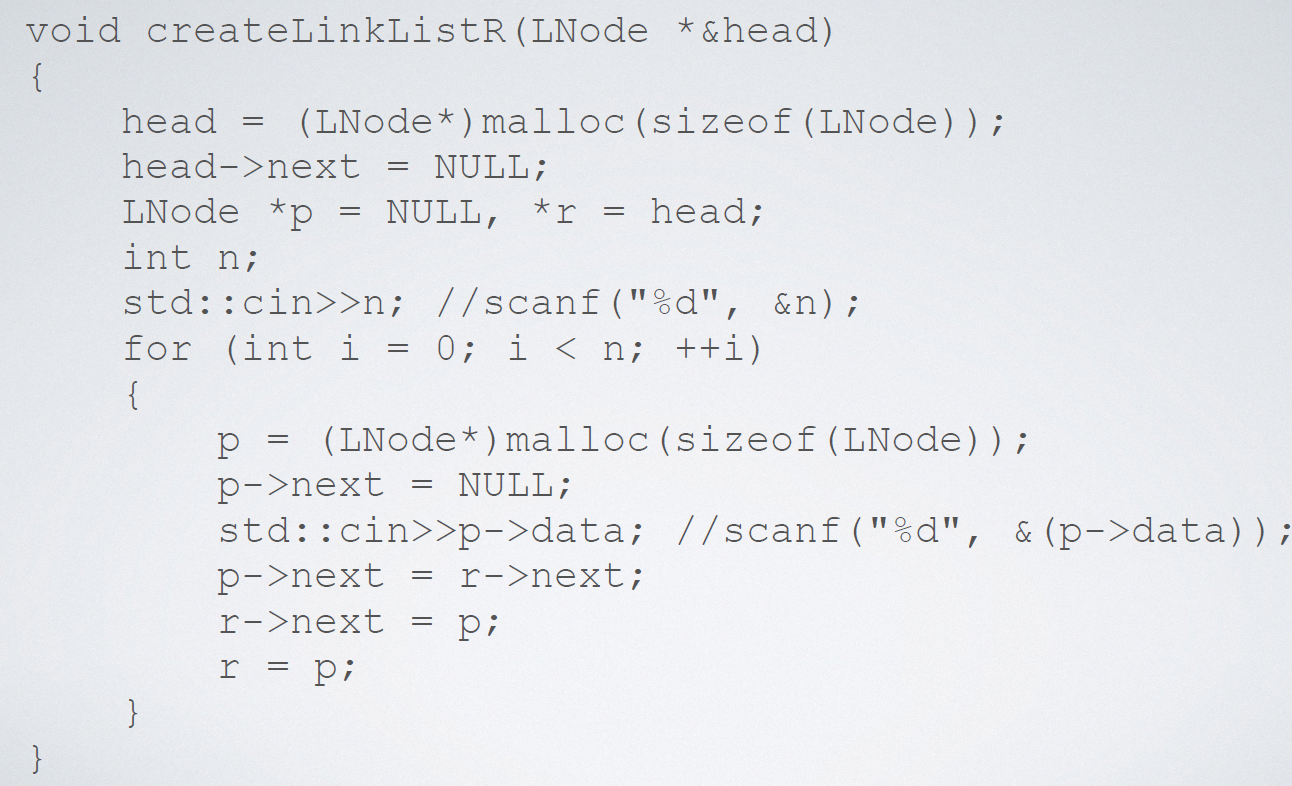
Implementation code (header insertion):

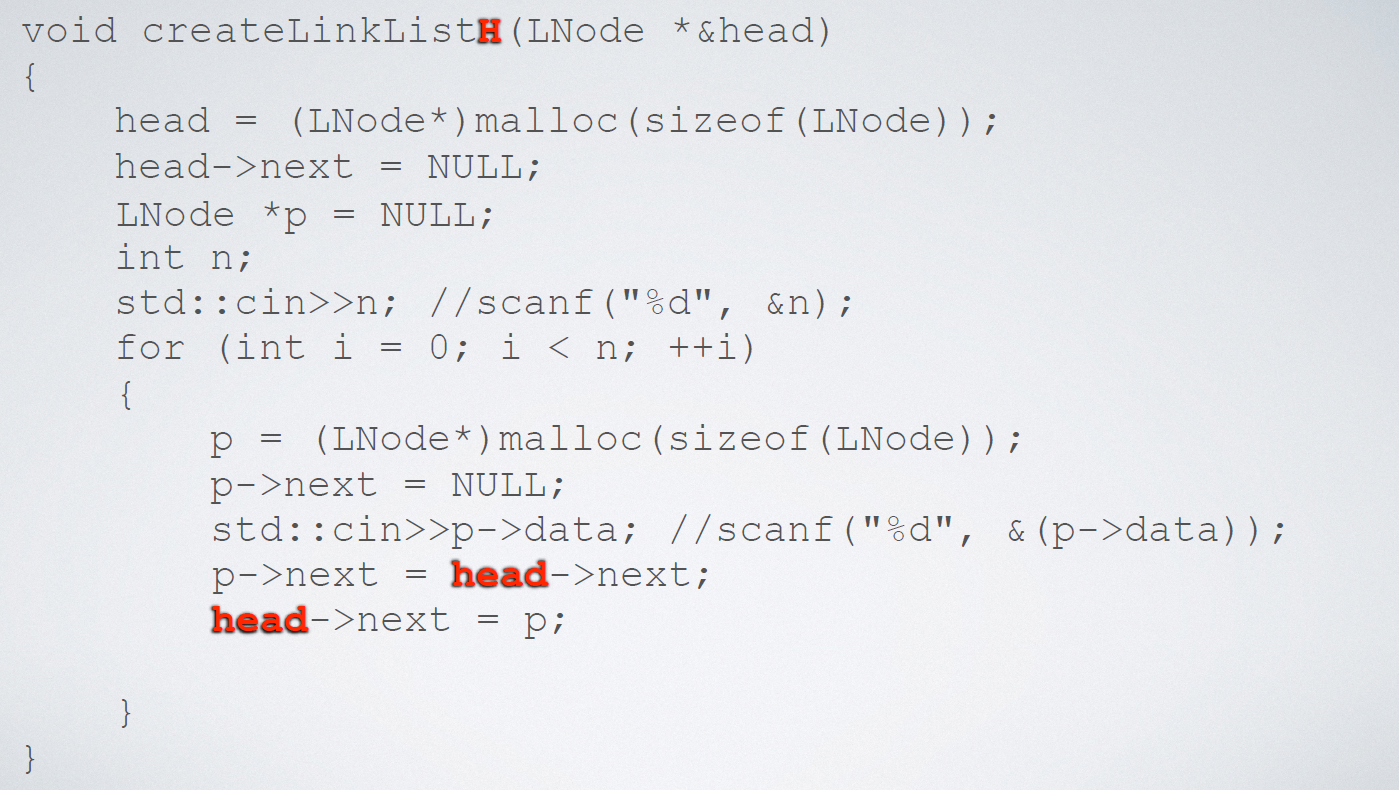
Exercise 5:

2.7 inverse problem

2.7.1 reverse setting of sequence table

Main implementation code:

for(int i = left,int j = right;i<j;++i,--j)
{
	temp = a[i];
	a[i] = a[j];
	a[j] = temp;
}

2.7.2 reverse linked list

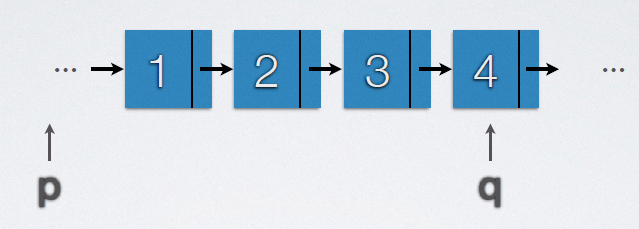
Main implementation code:

t = p->next;
p->next = t->next;
t->next = q->next;
q->next = t;
if(p->next ==q)
end;

Exercise 6:

1. Algorithm idea: first reverse the first P elements in R, then reverse the remaining elements, and finally reverse the whole R.

2.void reverse(int a[],int left,int right,int p)
{
	for(int i = left,int j = right;i<left+p&&i<j;++i,--j)
	{
		temp = a[i];
		a[i] = a[j];
		a[j] = temp;
	}
}
void solve(int a[],int n,int p)
{
	reverse(a,0,p-1,p);
	reverse(a,p,n-1,n-p);
	reverse(a,0,n-1,n);
}

3. Time complexity: O(n);
Spatial complexity: O(1);

In situ algorithm: the auxiliary space is a constant algorithm relative to the amount of input data

2.8 take the maximum value

2.8.1 maximum value of sequence table

Main implementation code:

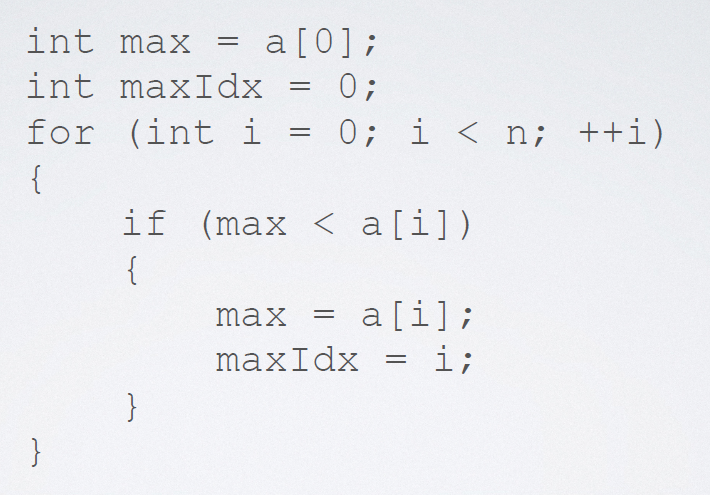
The minimum value can be changed to the details;

2.8.2 maximum value of linked list

Main implementation code:

LNode *p,*q;
int max = head->next->data;
q = p = head->next;
while(p!=NULL)
{
	if(max < p->data)
	{
		max = p->data;
		q = p;
	}
	p = p->next;
}

Exercise 7:

Implementation code:
void maxFirst(DLNode *head)
{
	## get max 
	DLNode *p = head->rlink,*q = p;
	int max = p->data;
	while(p!=NULL)
	{
		if(max<p->data)
		{
			max = p->data;
			q = p;
		}
		p = p->rlink;
	}
	----------------------------------------
	##delete
	DLNode *l = q->llink,*r = q->rlink;
	l->rlink = r;
	if(r!=NULL)
		r->llink = l;
	----------------------------------------	
	##insert
	q->llink = head;
	q->rlink = head->rlink;
	head->rlink = q;
	q->rlink->llink = q;
}

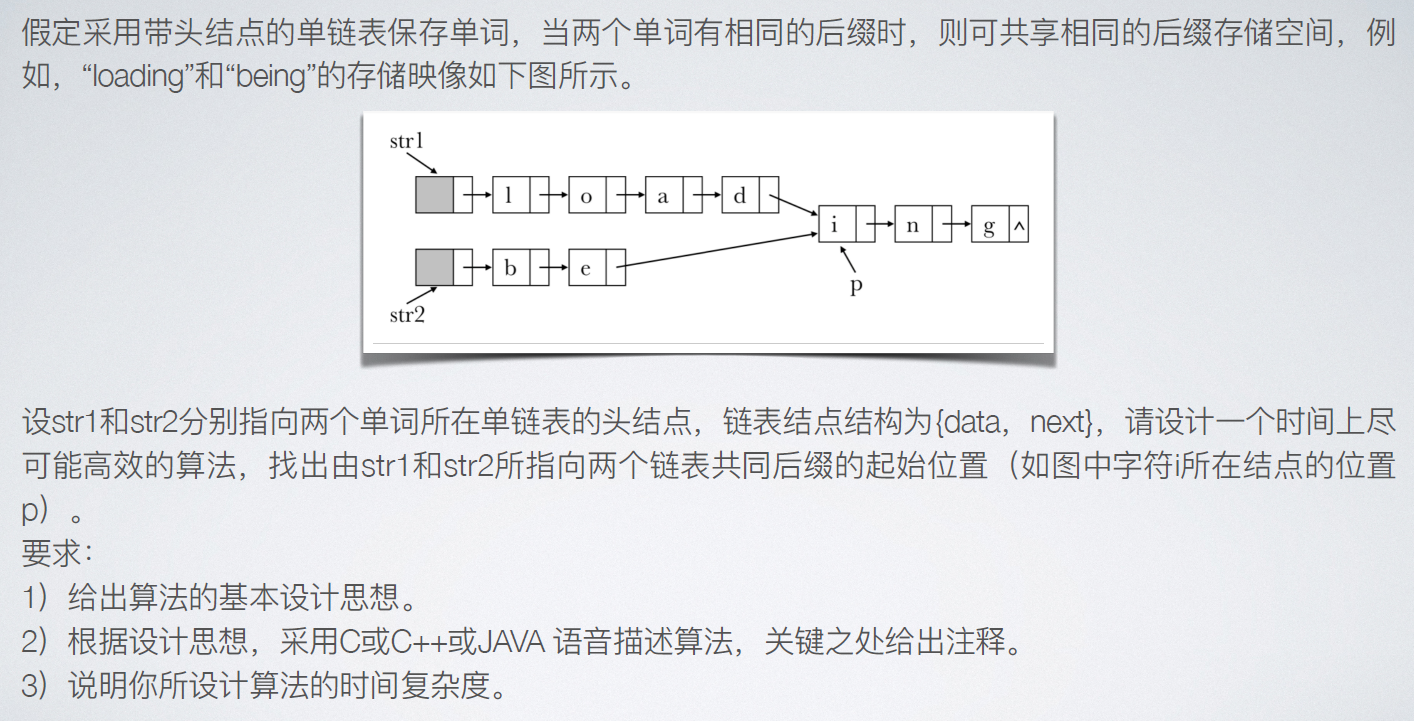
1. Basic idea of algorithm:
(1) Calculate the length of the two linked lists, len1 and len2;
(2) Make the pointers p and q point to the head node of str1 and str2 respectively. If M > = n, make p point to the m-n+1 node in the linked list; If M < n, make q point to the n-m+1 node in the linked list; Even if the length from the node to the end of the table indicated by pointers p and q is equal.
(3) Move the pointers p and q backward synchronously and judge whether they point to the same node. If p and q point to the same node, the point is the starting position of the common suffix.

2.LNode *solve(LNode *str1,LNode *str2)
{
	int len1 = 0,len2 = 0;
	LNode *p = str1->next,*q = str2->next;
	while(p!=NULL)
	{
		len1++;
		p = p->next;
	}
	while(q!=NULL)
	{
		len2++;
		q = q->next;
	}
	for(p = str1->next;len1>len2;len1--)
		p = p->next;
	for(q = str2->next;len1<len2;len2--)
		q = q->next;
	while(p!=NULL&&p!=q)
	{
		p = p->next;
		q = q->next;
	}
	return p;
}

3. The time complexity is O(n)

2.9 Division

Give a sequence table with the first element as the pivot so that the elements on the left are smaller than the pivot and the elements on the right are larger than the pivot

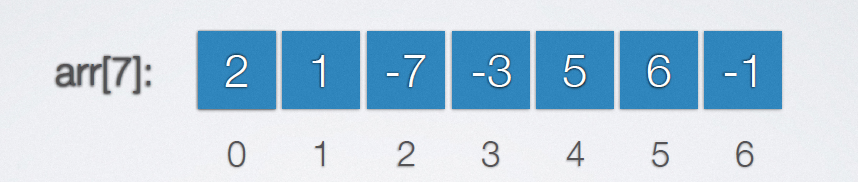
Thought:

First, define a temp constant, assign the pivot to temp, and then define the positions i, J, i < J at both ends of the array. Move J scan to the left. If the number is smaller than the pivot, move it to i position, and then move i to the right. If an element larger than the pivot is found, move it to j position

Implementation code:

void partition(int arr[],int n)
{
	int temp;
	int i = 0,j = n-1;
	temp = arr[i];
	while(i<j)
	{
		while(i<j&&arr[j]>=temp)
		--j;
		if(i<j)
		{
			arr[i] = arr[j]
			++i；
		}
		while(i<j&&arr[i]<temp)
		++i;
		if(i<j)
		{
			arr[j] = arr[i]
			--j;
		}
	}
	arr[i] = temp;
}

The effect is to divide the array elements into two parts with Y as the boundary. The first half is less than Y and the second half is greater than or equal to Y;
i and j end up pointing to X, not Y.
Exercise 8:
There is a linear table, which is stored by the single linked table L of the leading node. Design an algorithm to reverse it. It is required that no new nodes can be created, but only through the re combination of existing nodes in the table.

Implementation code:

LNode *p = head->next,*q;
L->next = NULL;
while(p!=NULL)
{
	q = p->next;
	p->next = L->next;
	L->next = p;
	p = q;
}

Write a function to print the data in the single linked list in reverse order, assuming that the pointer L points to the start node of the single linked list
Implementation code:

void reprint (LNode *L)
{
	if(L!=NULL)
	{
		reprint(L->next);
		cout<<L->data<<" ";
	}
}

2.10 consolidation

2.10.1 merging of sequence tables

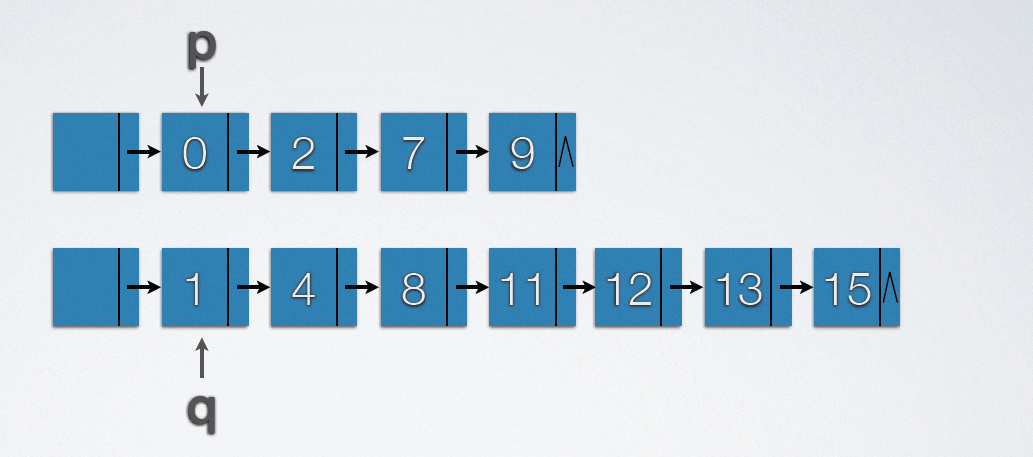
Implementation code:

void mergearray(int a[],int m,int b[],int n,int c[])
{
	int i,j = 0;
	int k = 0;
	while(i < m&&j<n)
	{
		if(a[i]<b[j])
			c[k++] = a[i++];
		else
			c[k++] = b[j++];
	}
	while(i<m)
		c[k++] = a[i++];
	while(j<n)
		c[k++] = b[j++];
}

2.10.2 list merging

Implementation code (tail interpolation):

void merge(LNode *A,LNode *B,LNode *&C)
{
	LNode *p = A->next;
	LNode *q = B->next;
	LNode *r;
	C = A;
	C->next = NULL;
	free(B);
	r = C;
	while(p!= NULL&&q!=NULL)
	{
		if(p->data<=q->data)
			r->next = p; p = p->next;
			r = r->next;
		else
			r->next = q; q = q->next;
			r = r->next;
	}
	if(p!=NULL)
		r->next = p;
	if(q!=NULL)
		r->next = q;
}

Implementation code (header insertion): merge in reverse order

void mergeR(LNode *A,LNode *B,LNode *&C)
{
	LNode *p = A->next;
	LNode *q = B->next;
	LNode *s;
	C = A;
	C->next = NULL;
	free(B);
	while(p!= NULL&&q!=NULL)
	{
		if(p->data<=q->data)
			s = p;p = p->next;
			s->next = C->next;
			C->next = s;
		else
			s = q;q = q->next;
			s->next = C->next;
			C->next = s;
	}
	while(p!=NULL)
		s = q;q = q->next;
		s->next = C->next;
		C->next = s;
	while(q!=NULL)
		s = q;q = q->next;
		s->next = C->next;
		C->next = s;
}