A references
- Book "sword finger offer (Second Edition)"
Search in JZ01 binary array
1. Title Description
In a two-dimensional array (each one-dimensional array has the same length), each row is sorted in ascending order from left to right, and each column is sorted in ascending order from top to bottom. Please complete a function, input such a two-dimensional array and an integer, and judge whether the array contains the integer.
[ [1,2,8,9], [2,4,9,12], [4,7,10,13], [6,8,11,15] ] given target = 7,return true. given target = 3,return false.
Example 1
input 7,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]] Return value true explain Exist 7, return true
2. Violence resolution
Of course, the easiest thing to think of is violent solution, which is to search one by one. If it is found, it returns true, and if it is not found, it returns false. The code is very simple and there is nothing to say.
public boolean findNumberIn2DArray(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return false;
}
int rows = matrix.length, columns = matrix[0].length;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
if (matrix[i][j] == target) {
return true;
}
}
}
return false;
}
3. Linear search
It is said in the question that each row is incremented and each column is incremented. So we can use this feature when searching. If we start from the upper left corner, when the target value is greater than the current value, we need to look for a larger value, but at this time, whether looking to the right or down is greater than the current value, so we can't determine which direction to look for. Similarly, the lower right corner is the same, so we can only start from the upper right corner or the lower left corner. Let's use the above data. When the target is equal to 23, start from the upper right corner and draw a picture
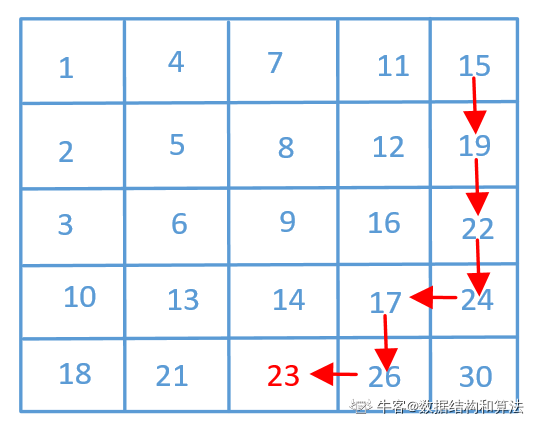
A convenient place to start from the upper right corner is that the ones on his left are smaller than him, and the ones below him are larger than him. If the target is greater than the current value, we will look down. If the target is less than the current value, we will look to the left to see the code.
public boolean Find(int target, int[][] array) {
if (array == null || array.length == 0 || array[0].length == 0) {
return false;
}
int rows = array.length, col = array[0].length;
//Start with the number in row 1 - col, which is the last column
int row = 0;
int column = col - 1;
while (row < rows && column >= 0) {
//num represents the current value
int num = array[row][column];
if (num == target) {
//If found, return directly
return true;
} else if (num > target) {
//Find before
column--;
} else {
//Find below
row++;
}
}
return false;
}
Of course, it is also possible to search from the lower left corner, because the value on the right side of the lower left corner is larger than him, and the value on the upper side is smaller than him. It can also be distinguished. The code is similar to that above. Let's see
public boolean Find(int target, int[][] array) {
if (array == null || array.length == 0 || array[0].length == 0) {
return false;
}
int rows = array.length, col = array[0].length;
int row = rows - 1;
int column = 0;
while (row >= 0 && column < col) {
int num = array[row][column];
if (num == target) {
//If found, return directly
return true;
} else if (num > target) {
//Look up
row--;
} else {
//Look to the right
column++;
}
}
return false;
}
JZ02 replace spaces
1. Title Description
Please implement a function to replace each space in a string with "% 20". For example, when the string is Then the replaced string is We%20Are%20Happy.
Example 1
input "We Are Happy" Return value "We%20Are%20Happy"
2.String.replaceAll()
Directly call the encapsulation method of String
public String replaceSpace (String s) {
if (s == null || "".equals(s))
return s;
return s.replaceAll(" ", "%20");
}
3.Spring.split()
Conventional method, split and replace
public String replaceSpace (String s) {
StringBuilder sb = new StringBuilder();
if (s == null || "".equals(s))
return s;
String[] strs = s.split("");
for (String str : strs) {
if (" ".equals(str))
sb.append("%20");
else
sb.append(str);
}
return sb.toString();
}
4. Traditional solution
Although the parameters in the Java version are passed into the String class, unlike the C language, it is a character array directly, and it cannot be expanded directly behind the array. However, you can actually use the StringBuffer class to implement such operations. The specific ideas have been explained in the book. Here we mainly post the program to introduce the implementation of Java.
pubilc class Solution{
pubilc String replaceSpace(String s){
if(s == null){ return null; }
StringBuffer str = new StringBuffer(s);
int length = str.length();
int spaceNum = 0;
for(int i = 0;i < length;i++){ if(str.charAt(i) == ' '){ spaceNum++; } }
int oldStr = length - 1;
length += 2 * spaceNum;
int newStr = length - 1;
str.setLength(length);
while(spaceNum > 0 && newStr >= 0){
char ch = str.charAt(oldStr--);
if(ch == ' '){
str.setCharAt(newStr--,'0');
str.setCharAt(newStr--,'2');
str.setCharAt(newStr--,'%');
spaceNum--;
}
else{ str.setCharAt(newStr--,ch); }
}
return str.toString();
}
}
JZ03 print linked list from end to end
1. Title Description
Enter a linked list and return an ArrayList from end to end.
Example 1
input
{67,0,24,58}
Return value
[58,24,0,67]
2. Problem solving
1, Non recursive
1. Analysis
listNode is a linked list, which can only traverse from beginning to end, but the output requires from end to end. This is a typical "first in and last out". We can think of stack! One method in ArrayList is add(index,value), which can specify the index position and insert the value value. Therefore, while traversing listNode, we insert each encountered value into the 0 position of the list, and finally output listNode to get the reverse linked list
2. Code
import java.util.*;
public class Solution {
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
ArrayList<Integer> list = new ArrayList<>();
ListNode tmp = listNode;
while(tmp!=null){
list.add(0,tmp.val);
tmp = tmp.next;
}
return list;
}
}
3. Complexity
Time complexity: O(n^2)
Spatial complexity: [the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-ndugq35t-1620795871448)( https://cdn.nlark.com/yuque/0/2021/svg/2196885/1618720921537-2de5fdce-dc30-44be-ad76-d8119b027bde.svg )]
2, Recursion
1. Analysis
Since non recursion has been realized, we can also use recursion to print with the help of the "stack" of the system
2. Code
import java.util.*;
public class Solution {
ArrayList<Integer> list = new ArrayList();
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
if(listNode!=null){
printListFromTailToHead(listNode.next);
list.add(listNode.val);
}
return list;
}
}
3. Complexity
Time complexity: [the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-imh3fr4w-1620795871450)( https://cdn.nlark.com/yuque/0/2021/svg/2196885/1618720921566-b2ef8ff7-8760-41ef-ad2c-76725b493c08.svg )]
Spatial complexity: [the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-h21ye6vt-1620795871452)( https://cdn.nlark.com/yuque/0/2021/svg/2196885/1618720921579-3b6e130a-420f-4a18-9d2e-e57d90f82d74.svg )]
2.ArrayList detailed explanation, read this article is enough
4.Format description of advanced data structure of Niuke programming problem (to be sorted out)
JZ04 rebuilding binary tree
1. Title Description
Enter a linked list and return an ArrayList from end to end.
Example 1
input
{67,0,24,58}
Return value
[58,24,0,67]
2. Problem solving 1
The key is: use the root node of the preorder sequence to find the root node in the front, and use the root node to divide the preorder sequence into two parts. The left part is the left subtree and the right part is the right subtree. Then use the length of the subtree to the pre order sequence, find the left and right subtrees in the pre order sequence, and find the root node at the same time. This step is performed recursively. If the length of the subtree is 0, there is no need to generate a sub problem.
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
/**
* The key is: use the root node of the preorder sequence to find the root node in the front, and use the root node to divide the preorder sequence into two parts. The left part is the left subtree and the right part is the right subtree. Then use the length of the subtree to the pre order sequence, find the left and right subtrees in the pre order sequence, and find the root node at the same time. This step is performed recursively. If the length of the subtree is 0, there is no need to generate a sub problem.
*/
public class Solution {
public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
TreeNode root = new TreeNode(pre[0]);
build(root, pre, 0, pre.length, in, 0, in.length);
return root;
}
/**
* Recursion and dichotomy divide the problem until it is easy to solve.
* The method is as follows: for a root node, first go to the middle order sequence to find the location of the value of the root node, and use this location to divide it into two parts. The length of the middle order sequence in the left part is the length of the middle order sequence in the left part of the previous sequence, and so is the right part.
* Then start generating subproblems. If the sequence length is 0, there is no need to generate subproblems. Otherwise: use the property that the first element of the preorder sequence is the root node to generate the root node, and then construct the subproblem.
* @param root Root node
* @param pre The pre sequence range is [pleft, price)
* @param in The range of middle order sequence is [ileft,iright)
*/
public void build(TreeNode root, int[] pre, int pleft, int pright, int[] in, int ileft, int iright) {
int i;
for (i = ileft; i < iright; i++) {
if (in[i] == root.val) {//Find the location of the root node from the middle order sequence
break;
}
}
int t = i - ileft;
if (t > 0) {//When the length of subtree is 0, there is no need to generate subproblems
root.left = new TreeNode(pre[pleft + 1]);
build(root.left, pre, pleft + 1, pleft + 1 + t, in, ileft, i);
}
if (pright - pleft - 1 - t > 0) {
root.right = new TreeNode(pre[pleft + 1 + t]);
build(root.right, pre, pleft + 1 + t, pright, in, i + 1, iright);
}
}
}
At present, the error array is out of bounds. It should be that the index is not completely right. This method is really the best to draw the picture
3. Problem solving 2
Idea:
Pre order traversal: root → left → right middle order traversal: left → root → right
-
The root node is 1 according to the preorder traversal sequence pre={1,2,4,7,3,5,6,8};
-
Then find 1 in the middle order traversal sequence in={4,7,2,1,5,3,8,6}, and you can see that the left side of 1 is the left subtree and the right side of 1 is the right subtree;
-
Recursive call: regard the left subtree and the right subtree as a tree respectively, and pass their pre order traversal sequence and middle order traversal sequence into the method respectively to obtain the root node of the left subtree and the root node of the right subtree. At this time, you need to connect them with the root node obtained in the first step;
-
Termination condition of recursive call: until the incoming array is empty, it indicates that there are no nodes, and null is returned directly.
import java.util.Arrays;
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
//Termination condition of recursive call
if(pre.length == 0 || in.length == 0){
return null;
}
//The root node of the binary tree is obtained from the preorder traversal
TreeNode root = new TreeNode(pre[0]);
//Find the location of the root node in the middle order traversal and divide the left and right subtrees
for(int i = 0; i < in.length; i++){
if(root.val == in[i]) {
//Treat the left subtree as a binary tree and call this method to get the root node of the left subtree, that is, the left child node of the upper root node
root.left = reConstructBinaryTree(Arrays.copyOfRange(pre,1,i+1),Arrays.copyOfRange(in,0,i));
//Treat the right subtree as a binary tree and call this method to get the root node of the right subtree, that is, the right child node of the upper root node
root.right = reConstructBinaryTree(Arrays.copyOfRange(pre,i+1,pre.length),Arrays.copyOfRange(in,i+1,in.length));
//Find the root node and jump out of the loop
break;
}
}
//Return root node
return root;
}
}
1.About arrays. Net in Java Copyofrange() method
JZ04 rebuilding binary tree
1. Title Description
Enter a linked list and return an ArrayList from end to end.
Example 1
input
{67,0,24,58}
Return value
[58,24,0,67]
2. Problem solving 1
3. Problem solving 2
JZ04 rebuilding binary tree
1. Title Description
Enter a linked list and return an ArrayList from end to end.
Example 1
input
{67,0,24,58}
Return value
[58,24,0,67]
2. Problem solving 1
3. Problem solving 2
JZ04 rebuilding binary tree
1. Title Description
Enter a linked list and return an ArrayList from end to end.
Example 1
input
{67,0,24,58}
Return value
[58,24,0,67]