Example 1: the number of m before output:

describe
Given that an array contains n elements, count the number of the first m, and output the M numbers from large to small.
input
The first line contains an integer n that represents the size of the array. n < 100000. The array contains an integer, separated by a space in the second row. The absolute value of each integer does not exceed 100000000. The third line contains an integer M. m < n.
output
From large to small, output the first m large number, one line for each number.

Method 1: merge and sort all numbers, and output the code of the first m large number (O(nlogn)):

#include <iostream>
using namespace std;
int a[1000000],temp[1000000];
void Merge(int *a,int s,int e,int m,int *tmp){
    int pb = 0;
    int p1 = s,p2 = e;
    while(p1<=m&&p2<=e){
        if(a[p1]<a[p2]){
        
            tmp[pb++] = a[p1++];
        }else{
            tmp[pb++] = a[p2++];
        }
    }
    while(p1<=m){
        tmp[pb++] = a[p1++];
        
    }
    while(p2<=e){
        tmp[pb++] = a[p2++];
    }
    for(int i = 0;i<e-s+1;i++){
        a[s+i] = tmp[i];
    }
}

void MergeSort(int *a,int s,int e,int *tmp){
    if(s < e)
    {
        int m = s+(e-s)/2;
        MergeSort(a,s,m,tmp);
        MergeSort(a,m+1,e,tmp);
        Merge(a,s,m,e,tmp);
    }
}

int main(){
    int n,m;
    while(cin>>n>>m){
        for(int i = 0;i<n;i++){
            cin>>a[i];
        }
        MergeSort(a,0,n-1,temp);
        for(int i = n-m;i<n;i++){
            if(i == n-m){
                cout<<a[i];
            }else{
                cout<<","<<a[i];
            }
        }
        cout<<endl;
    }
    return 0;
}

Method 2:
Divide and Conquer: complexity O(n+mlogm)
Idea: get the top m elements to the rightmost side of the array, then sort the rightmost m elements, and then output them
Key: in O(n) time, all the top m are moved to the rightmost side of the array
Introduction operation arrangeRight(k): get the first k of the array (or part of the array) to the far right
How to get the top k big ones to the far right
1) Set key=a[0], move the key to the appropriate position, so that the elements smaller than the key are on the left of the key and the elements larger than the key are on the right of the key (linear time completion) - that is, use a quick sorting process
2) Select the front or rear of the array and then perform the arrangeRight operation

a = k done indicates completion of the process
A > k: arrangeright (k) for this a element
A < K, arrange right (K-a) for the left b elements

(this place introduces images to deepen thinking)

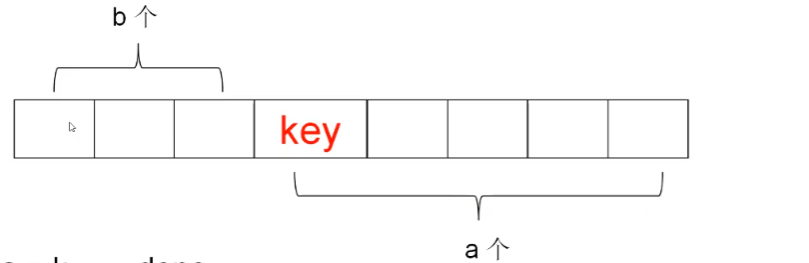
The number of a is larger than the key, and the number of b is smaller than the key. Now start to compare the distribution of the first k numbers in this array. There are three cases. The first case is k==a, which means that the first a just meets the requirements of the topic. If a > k, it means that you just need to find arrangeRight(k) on the right again. If a < K, you need to find another a on the left b elements on the right, Then there are only k-a on the left (note that the left is a whole at this time). The code will be explained later

#include <iostream>
using namespace std;
int a[1000000],temp[1000000];
void Merge(int *a,int s,int e,int m,int *tmp){
    int pb = 0;
    int p1 = s,p2 = e;
    while(p1<=m&&p2<=e){
        if(a[p1]<a[p2]){
        
            tmp[pb++] = a[p1++];
        }else{
            tmp[pb++] = a[p2++];
        }
    }
    while(p1<=m){
        tmp[pb++] = a[p1++];
        
    }
    while(p2<=e){
        tmp[pb++] = a[p2++];
    }
    for(int i = 0;i<e-s+1;i++){
        a[s+i] = tmp[i];
    }
}

void MergeSort(int *a,int s,int e,int *tmp){
    if(s < e)
    {
        int m = s+(e-s)/2;
        MergeSort(a,s,m,tmp);
        MergeSort(a,m+1,e,tmp);
        Merge(a,s,m,e,tmp);
    }
}

void arrangeRight(int *a,int s,int e,int k){
    if(s>=e){
        return 0;
    }
    int t = a[s];
    int i =s,j = e;
    while(i != j){
        while(i < j && t <= a[j]){
            --j;
        }
        swap(a[i],a[j]);
        while(i<j && t >= a[i]){
            i++;
        }
        swap(a[i],a[j]);
    }
    //this i The end is in the middle 
    int num = e-i+1;
    if(num == k){
        return;
    }
    if(num>k){
        arrangeRight(a,i+1,e,k);
    }
    if(num<k){
        arrangeRight(a,s,i-1,k-num);
    } 
    
    
    
}

int main(){
    int n,m;
    while(cin>>n>>m){
        for(int i = 0;i<n;i++){
            cin>>a[i];
        }
        arrangeRight(a,0,n-1,m);
        MergeSort(a,n-m,n-1,temp);
        for(int i = n-m;i<n;i++){
            if(i == n-m){
                cout<<a[i];
            }else{
                cout<<","<<a[i];
            }
        }
        cout<<endl;
    }
    return 0;
}

Note that the arrangeRight function only puts all the first m numbers on the right. Once the total quantity reaches m, it will return. As long as the data scale is large enough, the speed in the back will be much faster than that in the front.

Code reference: (92 messages) number of the first m output_ Jamence's blog - CSDN blog