Source of ideas with score https://blog.csdn.net/qq_51118755/article/details/122680838

With score

Title Description
100 Can be expressed as a fraction: 100 = 3 + 69258 / 714

It can also be expressed as:100 = 82 + 3546 / 197

Attention Feature: Number 1 in score~9 Occurs separately and only once (excluding 0).

Like this with fractions, 100 has 11 representations.

Enter a description
 Read in a positive integer from standard input N(N<1000). 

Output Description
 Program outputs this number using number 1~9 Do not repeat and do not omit all the species represented by fractions.

Note: There is no requirement to output each representation, just count how many!

Input and Output Samples
 Example
 input

100

output

11

Run Restrictions
 Maximum run time: 3 s
 Maximum Running Memory: 64M

Analysis

• dfs plus full sorting problem, easy to timeout so consider pruning!!!

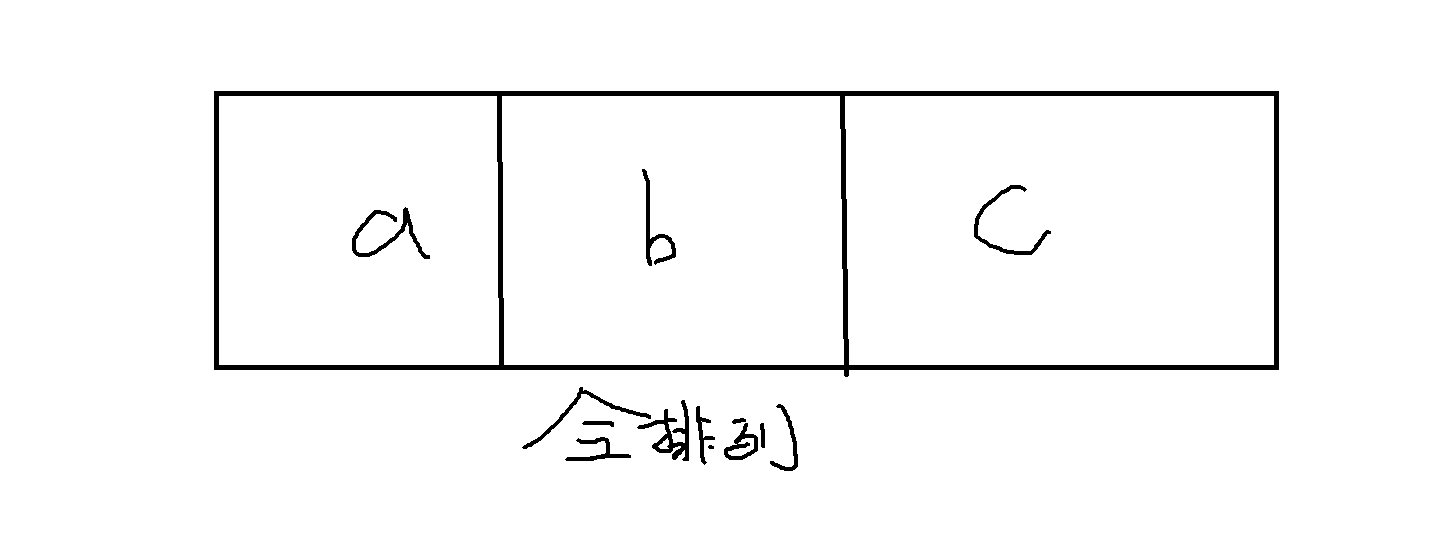
Note that the entire arrangement after cutting will contain all the values a,b,c (which is magical in pruning)

• Formula abstract: n = a + b / c
• Since n is a fixed value and B / C > 0, n > a, so len (n) >= len (a), here we have determined the maximum cutting range of A.
• We get a from the cutting range of a, so b/c is a fixed value. If I can confirm c, B will come out automatically. Note here, however, that the cutting range may still be large and must be cut again through all operations. Remember: the whole permutation after cutting will contain all the values of a, B and c, so here we use the last digit as the end of c, and the end of C knows that we c a n directly find the end of B with the formula: c*(n-a)%10. If the end number equals 0 and the end number equals the end of c, then we c a n continue directly.
• What's the use of knowing the last number of b? You can know the cutting range of B and find the position of the tail number of B. If the tail number of B is within the cutting range of a and the tail number of B is within the cutting range of C (in fact, this can not be used because there is a preceding judgment whether or not it is equal to the last position, so B must not be within the cutting range of c).
• The final step is to determine whether n = a + b / c is valid.
• The above operations require stitching, so it is more appropriate to use strings in the full arrangement, and the tuples can be stitched directly.

Run Code

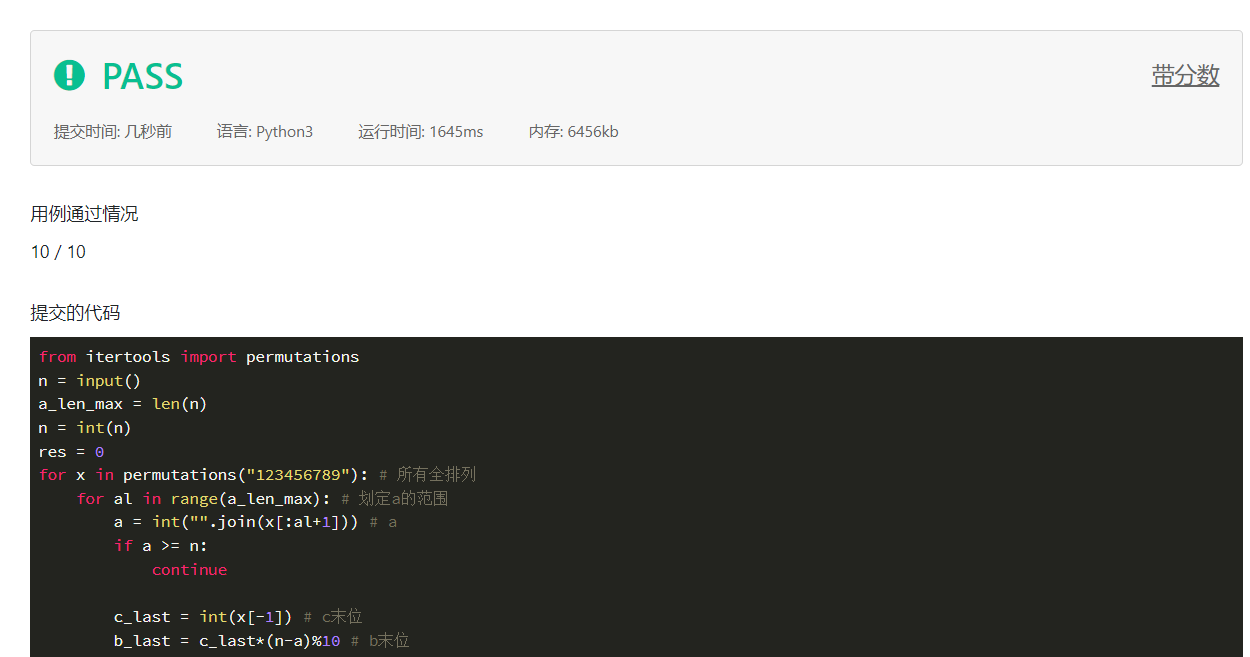
from itertools import permutations
n = input()
a_len_max = len(n) 
n = int(n)
res = 0
for x in permutations("123456789"): # All Full Arrangement
    for al in range(a_len_max): # Delimit a's range
        a = int("".join(x[:al+1])) # a
        if a >= n:
            continue
        
        c_last = int(x[-1]) # c-terminal
        b_last = c_last*(n-a)%10 # b-terminal
        if b_last == 0 or b_last == c_last:
            continue
        
        b_loc = x.index(str(b_last))
        if b_loc <= al : # Cutting range at a
            continue

        b = int("".join(x[al+1:b_loc+1]))
        c = int("".join(x[b_loc+1:]))
        if b / c + a == n:
            res+=1
print(res)  

By screenshot

Number of Serial Intervals

Title Description
 Xiao Ming has been thinking about such a strange and interesting question these days:

At 1 ~ N How many hyphenated intervals are there in a full permutation of?

The definition of the connected interval is as follows:

If Interval [L,R] All elements in the L First to First R Incrementally sort to get a length of R-L+1 Of"continuity"A number of columns is called the interval serial interval.

When N When he was very young, Xiao Ming could quickly figure out the answer, but when N When he got older, the problem was not so simple. Now Xiaoming needs your help.

Enter a description
 The first line is a positive integer N(1≤N≤50×10^4), Represents the full size of the arrangement.

The second line is N A different number Pi(1≤Pi≤N)，Indicate this N A Full Permutation of numbers.

Output Description
 Output an integer representing the number of distinct comma intervals.

Input and Output Samples
 Example
 input

4
3 2 4 1

output

7

Run Restrictions
 Maximum run time: 5 s
 Maximum Running Memory: 64M

Analysis

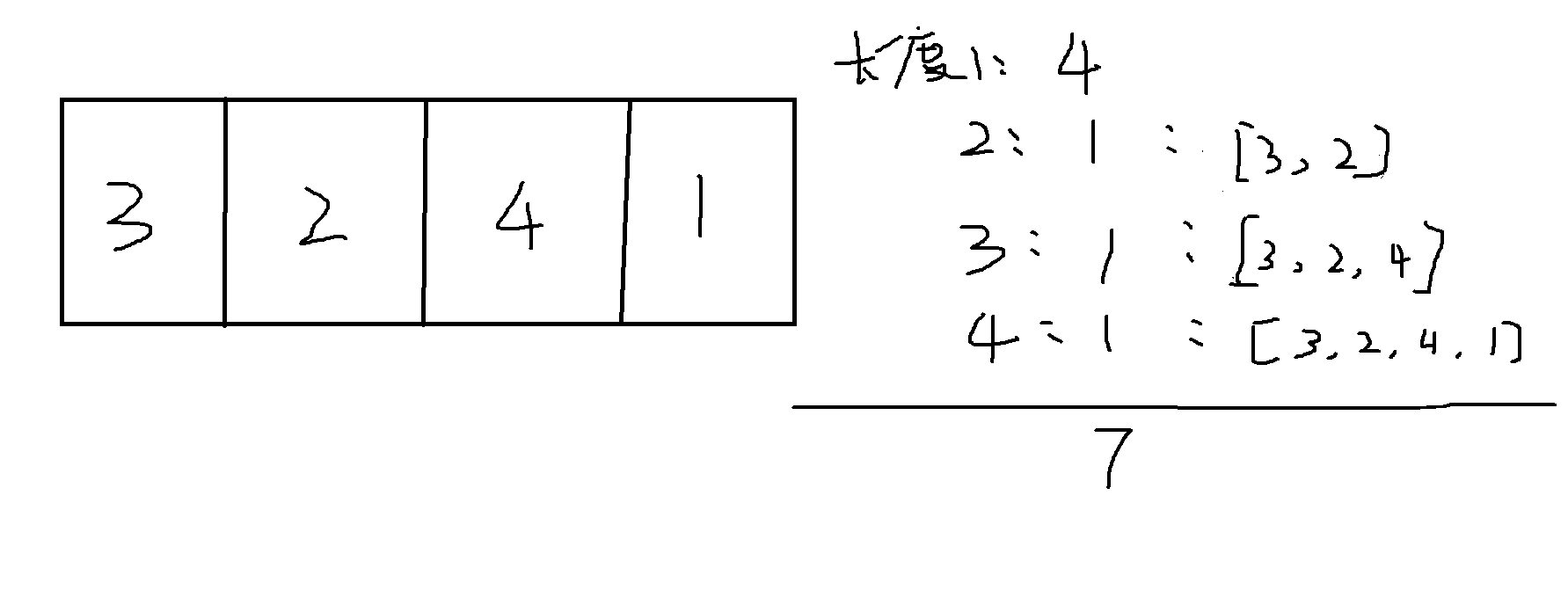
• The title is really incomprehensible. You can use the picture above to understand it directly. (I don't know why a number is also an incremental sort)
• Violence is easy to think of. As long as we find the maximum and minimum, then if the maximum minus the minimum equals the difference between interval locations, the condition must be met. Note here that the full array of numbers is not repeated

Run Code

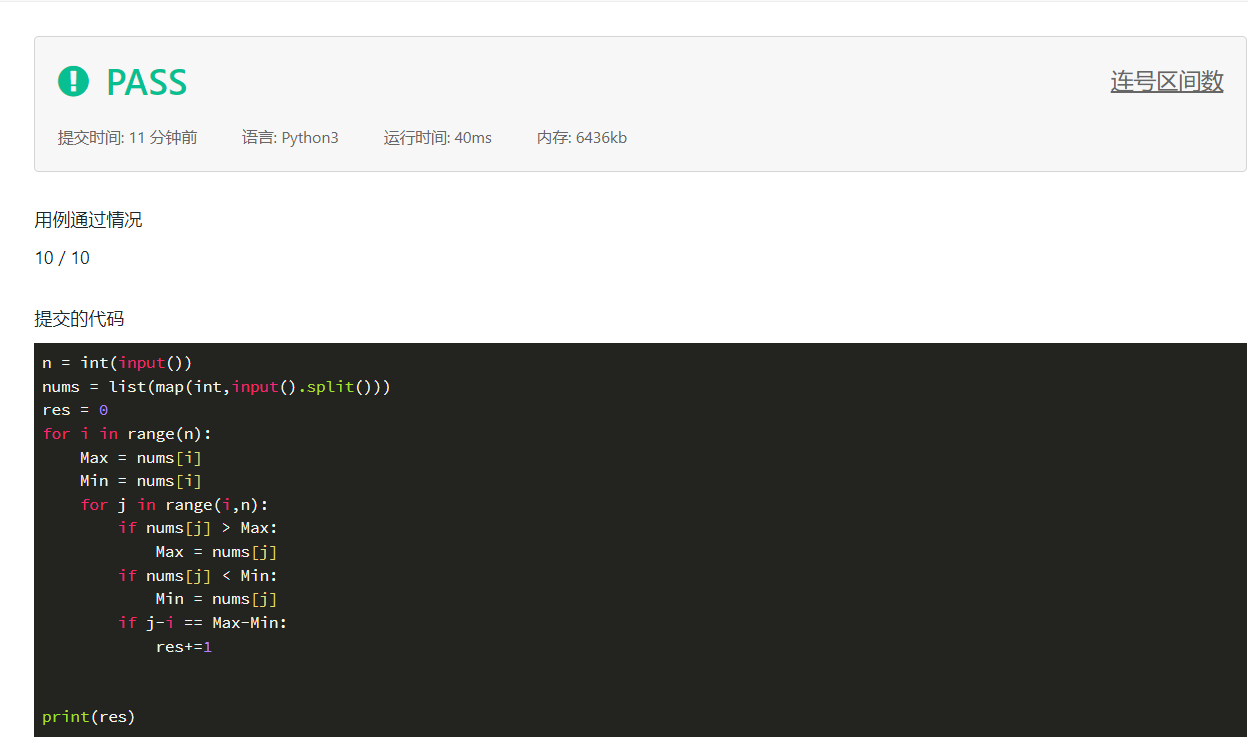
n = int(input())
nums = list(map(int,input().split()))
res = 0
for i in range(n):
    Max = nums[i]
    Min = nums[i]
    for j in range(i,n):
        if nums[j] > Max:
            Max = nums[j]
        if nums[j] < Min:
            Min = nums[j]
        if j-i == Max-Min:
            res+=1


print(res)

By screenshot

If there are any errors, please correct them and welcome to communicate. Thank you. ω･) ﾉ