On round square tree
Point biconnected component
definition
If an undirected graph does not change its connectivity by removing any node, that is, there is no cut point, it is called a point biconnected graph.
Every maximal vertex biconnected subgraph in an undirected graph is called the vertex biconnected component of the undirected graph.
Unlike strongly connected components, a point may belong to multiple point pairs, but an edge belongs to exactly one point pair.
Therefore, the biconnected components of our labeled points are often labeled edges.
Some changes in the round square tree
-
Define approximation: a graph with no points.
-
Different points: for a subgraph with two points and one edge. According to our definition at the beginning, he is not a dot double, but here, we think he is a dot double.
-
Note: using the following definition, there is still a point that may belong to multiple point pairs, but an edge belongs to exactly one point pair.
Round square tree
definition
-
All points in the original drawing are called dots.
-
For each point double connected component:
- Delete all the edges inside this point pair.
- Create a new square point.
- The square point connects the edge to the point in all double points.
-
Therefore, for the circular square tree, there are \ (n + c \) points in total, where \ (n \) is the number of points in the original graph and \ (c \) is the number of double connected components of the points in the original graph.
-
Basic properties: each edge of the square tree connects a circle point and a square point.
-
Refer to the following figure for details:
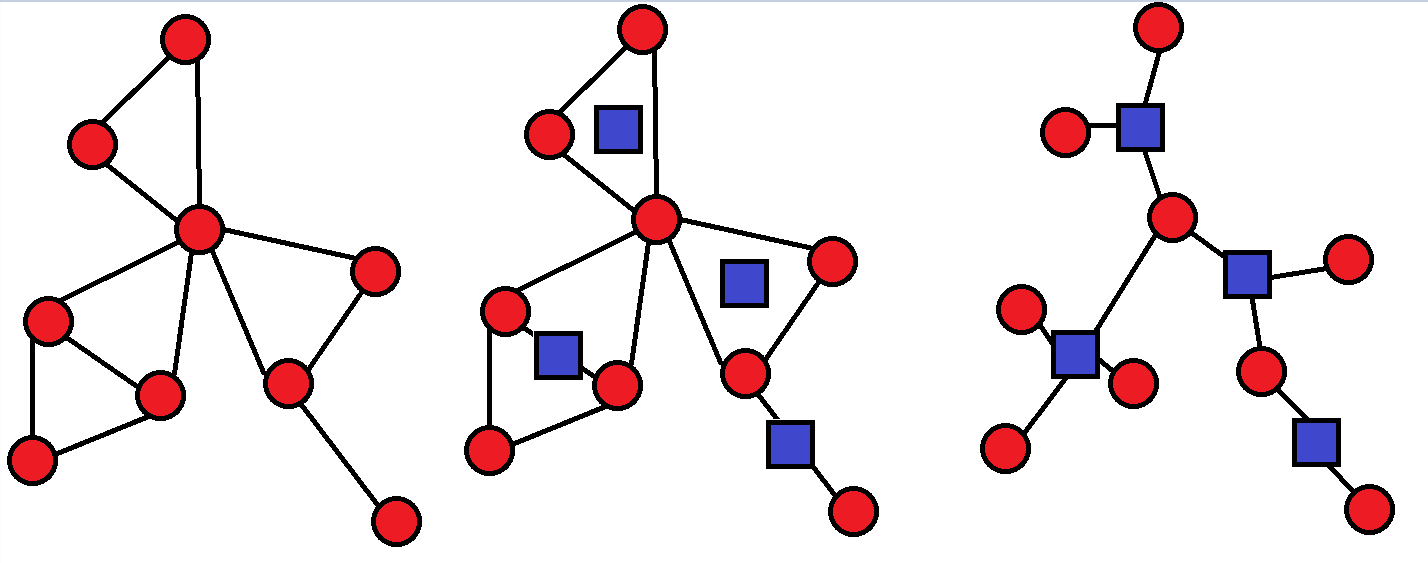
-
The number of round square trees is less than \ (2n \). Because the number of cut points is less than \ (n \).
-
Note: if the original picture is connected, the round square tree is a tree, otherwise, it is a forest.
structure
The algorithm used to build the round square tree is \ (tarjan \) algorithm. We use \ (dfn[u] \) to store the \ (DFS \) sequence of node \ (U \), that is, when we access \ (U \) for the first time, it is the first node to be accessed\ (low[u] \) stores the minimum \ (DFS \) order of a point \ (v \) in the sub tree of the \ (DFS \) tree of node \ (U \) that can be accessed by returning to the ancestral edge or to the father's tree edge at most once.
It is easy to notice that the difference between it and normal \ (tarjan \) lies in whether it can be updated through the tree edge.
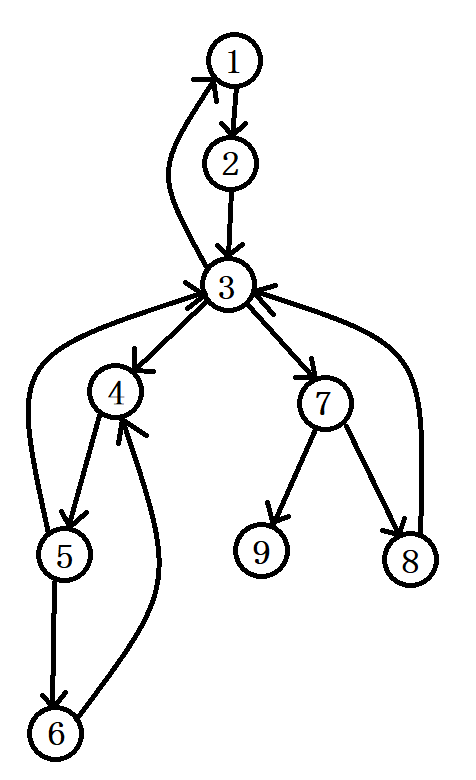
| u | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| low[u] | 1 | 1 | 1 | 3 | 3 | 4 | 3 | 3 | 7 |
It is easy to notice that the value of \ (low \) corresponding to \ (9 \) is different from that of normal \ (tarjan \).
The following is the code of normal \ (tarjan \):
inline void Tarjan(int u, int fa)
{
low[u] = dfn[u] = ++t;
//low is initialized as the current node dfn
for(register int v : G[u]){
if(!dfn[v]){ //If you haven't visited
Tarjan(v); //recursion
low[u] = min(low[u], low[v]);
}
else if(v != fa) low[u] = min(low[u], dfn[v]);
}
}
The following is the code of \ (tarjan \) in the round square tree:
inline void Tarjan(int u)
{
low[u] = dfn[u] = ++t;
//low is initialized as the current node dfn
for(register int v : G[u]){
if(!dfn[v]){ //If you haven't visited
Tarjan(v); //recursion
low[u] = min(low[u], low[v]);
}
else low[u] = min(low[u], dfn[v]);
}
}
Here, we learned how to build a round square tree.
Next are some examples.
[APIO2018] Triathlon
meaning of the title
Given a simple undirected graph, ask how many pairs of triples \ (< s,c,f > \) (\ (s,c,f \) are different from each other), so that there is a simple path from \ (s \), through \ (c \) to \ (f \).
Sol
-
Properties of point pairs: for two points in a point pair, the union of simple paths between them is exactly equal to this point pair. That is, there must be a simple path between different points \ (u,v \) in the same point pair through another given point \ (w \) in the same point pair.
-
This property tells us that considering the path of two dots on the square tree, the set of dots adjacent to the square points passing through the path is equal to the set of dots on the two simple paths in the original graph.
-
This makes us think of fixed \ (s,f \) and find the number of legal \ (c \). Obviously, the number of legal \ (c \) is equal to the number of points of the union of simple paths between \ (s,f \) minus \ (2 \) (that is, remove \ (s,f \) itself).
-
So we consider to construct the square tree of the original graph first. The number of \ (c \) between two points is related to the square points and dots they pass on the square tree. We consider assigning specific values to square points and circle points, that is, the weight of each square point is the size of the corresponding point pair, and the weight of each circle point is \ (- 1 \).
-
After this assignment, the sum of path weights on the square tree between the two dots is exactly equal to the union size of the simple path in the original figure minus \ (2 \). It is not difficult to understand that each square point of the path counts the weight of adjacent dots, but the dots passing through the middle will be repeatedly calculated, and the subtracted \ (1 \) will be just offset, but there is no such situation at the starting point and end point, so we subtracted \ (2 \).
-
Here, click tree \ (dp \).
-
Conclusion: in the square tree, we can often solve some complex problems by assigning values to points.
code
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 10;
inline int read()
{
int s = 0, w = 1;
char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') w *= -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
return s * w;
}
int n, m, t, rec, cnt, top, ans;
int sck[N], dfn[N], low[N], siz[N], sum[N];
vector<int> G[N], T[N];
inline void Sol(int pos, int fa)
{
siz[pos] = pos <= rec;
for(register int v : T[pos])
if(v != fa) Sol(v, pos), siz[pos] += siz[v];
if(pos <= rec){
ans += (cnt - 1) * (cnt - 1);
for(register int v : T[pos])
if(v != fa) ans -= sum[v];
}
else{
for(register int v : T[pos])
if(v != fa) sum[pos] += siz[v] * siz[v];
int tem = (cnt - siz[pos]) * (cnt - siz[pos]);
for(register int v : T[pos])
if(v != fa) ans -= sum[pos] - siz[v] * siz[v] + tem;
}
}
inline void Tarjan(int pos)
{
sck[++top] = pos, cnt++;
dfn[pos] = low[pos] = ++t;
for(register int v : G[pos]){
if(!dfn[v]){
Tarjan(v), low[pos] = min(low[pos], low[v]);
if(low[v] == dfn[pos]){
int tem = 0; n++;
while(tem != v){
tem = sck[top--];
T[n].push_back(tem), T[tem].push_back(n);
}
T[n].push_back(pos), T[pos].push_back(n);
}
}
else low[pos] =min(low[pos], dfn[v]);
}
}
signed main()
{
n = read(), m = read(), rec = n;
for(register int i = 1; i <= m; i++){
int x = read(), y = read();
G[x].push_back(y), G[y].push_back(x);
}
for(register int i = 1; i <= rec; i++){
if(dfn[i]) continue;
cnt = 0, Tarjan(i), Sol(i, 0);
}
printf("%lld\n", ans);
return 0;
}
[CodeFoces 487E] Tourists
meaning of the title
Given a simple undirected connected graph, two operations are required:
-
Modify the point weight of a point.
-
Ask the minimum value of point weight on all simple paths between two points.
Sol
-
After learning the round square tree and looking at the previous problem, we will look at this problem again. Naturally, we will have such an idea: build a round square tree for the original drawing, assign a value to the square point, assign the minimum value of all the dot values connected with it, and then add a set of line segment tree sets in the tree chain dissection. This problem seems to be finished.
-
Indeed, if there is no operation \ (1 \), we can simply complete this topic. However, the operation \ (1 \) does exist. Considering such an extreme situation, if I modify a dot every time, I will affect all square points adjacent to it. If there are enough square points adjacent to it, obviously, such complexity is unacceptable.
-
But soon we can think that since there are too many square points adjacent to it, we can limit this number, that is, limit the information we maintain. In fact, we can let the value of each dot only affect its father. Of course, according to the definition of the round square tree, its father must be a square dot. It is found that this will basically not affect our above process, but it effectively solves the problem of time complexity. Just note that when asking, if our \ (LCA \) is a square dot, Then take \ (min \) between the father dot of the square point and our answer.
code
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 4e5 + 10, INF = 1e18;
inline int read()
{
int s = 0, w = 1;
char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') w *= -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
return s * w;
}
int n, m, t, q, rec, cnt, tot;
int tr[4 * N];
int id[N], fa[N], dep[N], siz[N], top[N], son[N];
int arr[N], sck[N], dfn[N], low[N];
vector<int> G[N], T[N];
multiset<int> s[N];
//Establish square tree
inline void Tarjan(int pos)
{
sck[++tot] = pos, dfn[pos] = low[pos] = ++t;
for(register int v : G[pos]){
if(!dfn[v]){
Tarjan(v), low[pos] = min(low[pos], low[v]);
if(low[v] == dfn[pos]){
int tem = 0; n++;
while(tem != v){
tem = sck[tot--];
T[n].push_back(tem), T[tem].push_back(n);
}
T[n].push_back(pos), T[pos].push_back(n);
}
}
else low[pos] = min(low[pos], dfn[v]);
}
}
inline void dfs1(int u, int father)
{
fa[u] = father, dep[u] = dep[father] + 1, siz[u] = 1;
if(u <= rec && father) s[father].insert(arr[u]); //It's a dot. Only the father is recorded
for(register int v : T[u]){
if(v == father) continue;
dfs1(v, u);
siz[u] += siz[v];
if(siz[v] > siz[son[u]]) son[u] = v;
}
if(u > rec) arr[u] = *s[u].begin();
}
inline void dfs2(int u, int st)
{
top[u] = st, dfn[u] = ++cnt, id[cnt] = u;
if(son[u]) dfs2(son[u], st);
else return;
for(register int v : T[u])
if(v != fa[u] && v != son[u]) dfs2(v, v);
}
inline void update(int k) { tr[k] = min(tr[k << 1], tr[k << 1 | 1]); }
inline void build(int k, int l, int r)
{
if(l == r) { tr[k] = arr[id[l]]; return; }
int mid = (l + r) >> 1;
build(k << 1, l, mid), build(k << 1 | 1, mid + 1, r);
update(k);
}
inline void change(int k, int l, int r, int x, int v)
{
if(r < x || l > x) return;
if(l == r && l == x) { tr[k] = v; return; }
int mid = (l + r) >> 1;
change(k << 1, l, mid, x, v), change(k << 1 | 1, mid + 1, r, x, v);
update(k);
}
inline int ask(int k, int l, int r, int x, int y)
{
if(r < x || l > y) return INF;
if(l >= x && r <= y) return tr[k];
int mid = (l + r) >> 1;
return min(ask(k << 1, l, mid, x, y), ask(k << 1 | 1, mid + 1, r, x, y));
}
inline int query(int x, int y)
{
int res = INF;
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]]) swap(x, y);
res = min(res, ask(1, 1, n, dfn[top[x]], dfn[x]));
x = fa[top[x]];
}
if(dep[x] < dep[y]) swap(x, y);
res = min(res, ask(1, 1, n, dfn[y], dfn[x]));
if(y > rec) res = min(res, arr[fa[y]]);
return res;
}
signed main()
{
n = read(), m = read(), q = read(), rec = n, arr[0] = INF;
for(register int i = 1; i <= n; i++) arr[i] = read();
for(register int i = 1; i <= m; i++){
int x = read(), y = read();
G[x].push_back(y), G[y].push_back(x);
}
Tarjan(1), dfs1(1, 0), dfs2(1, 1), build(1, 1, n);
while(q--){
char opt[10]; cin >> opt;
int a = read(), b = read();
if(opt[0] == 'C'){
if(fa[a]){
auto it = s[fa[a]].find(arr[a]); s[fa[a]].erase(it), s[fa[a]].insert(b);
arr[fa[a]] = *s[fa[a]].begin(), change(1, 1, n, dfn[fa[a]], arr[fa[a]]);
}
arr[a] = b, change(1, 1, n, dfn[a], b);
}
else printf("%lld\n", query(a, b));
}
return 0;
}