https://www.cnblogs.com/InCerry/p/10325290.html
1, Foreword
In fact, the drawings and text of this article have been sorted out for a long time, but it has been delayed until now for various reasons. The notes of "multithreaded programming" previously set up Flag have also been written. It is just that it is still rough, so it needs to be sorted out in time to meet you.
I'm sure you are familiar with the Dictionary class in C #. It is a collection type that can store data in the form of key / value pairs. The biggest advantage of this class is that the time complexity of finding elements is close to O(1). In practical projects, it is often used for local caching of some data to improve the overall efficiency.
So what kind of design can make the Dictionary class realize the time complexity of O(1)? That is what this article wants to discuss with you; These are some personal understandings and views. If there are unclear and mistakes, please criticize and correct them and make common progress.
2, Theoretical knowledge
For the implementation principle of Dictionary, there are two key algorithms, one is Hash algorithm, and the other is used to deal with Hash collision and conflict resolution algorithm.
1. Hash algorithm
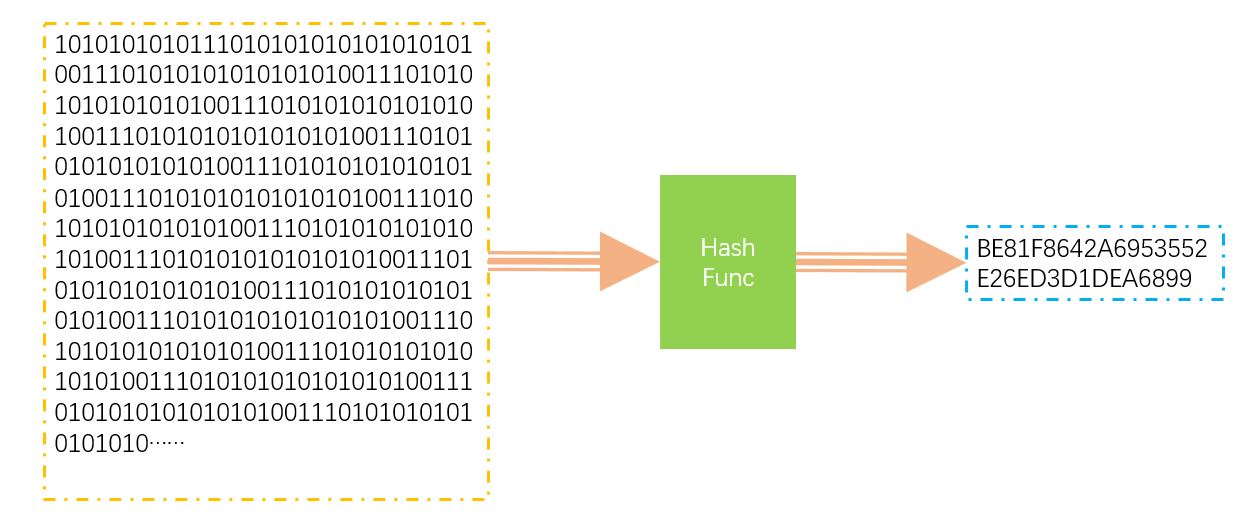
Hash algorithm is a digital summarization algorithm, which can map the binary data set with indefinite length to a shorter binary data set. The common MD5 algorithm is a hash algorithm, which can generate digital summarization for any data. The function that implements the hash algorithm is called the hash function. Hash function has the following characteristics.
- Hash operation is performed on the same data, and the results must be the same. HashFunc(key1) == HashFunc(key1)
- The results of Hash operation on different data may also be the same (Hash will produce collision). key1 != key2 => HashFunc(key1) == HashFunc(key2).
- The Hash operation is irreversible, and the key cannot obtain the original data. Key1 = > hashcode, but hashcode = \ = > key1.
The following figure is a simple illustration of the Hash function. Any length of data is mapped to a shorter data set through HashFunc.
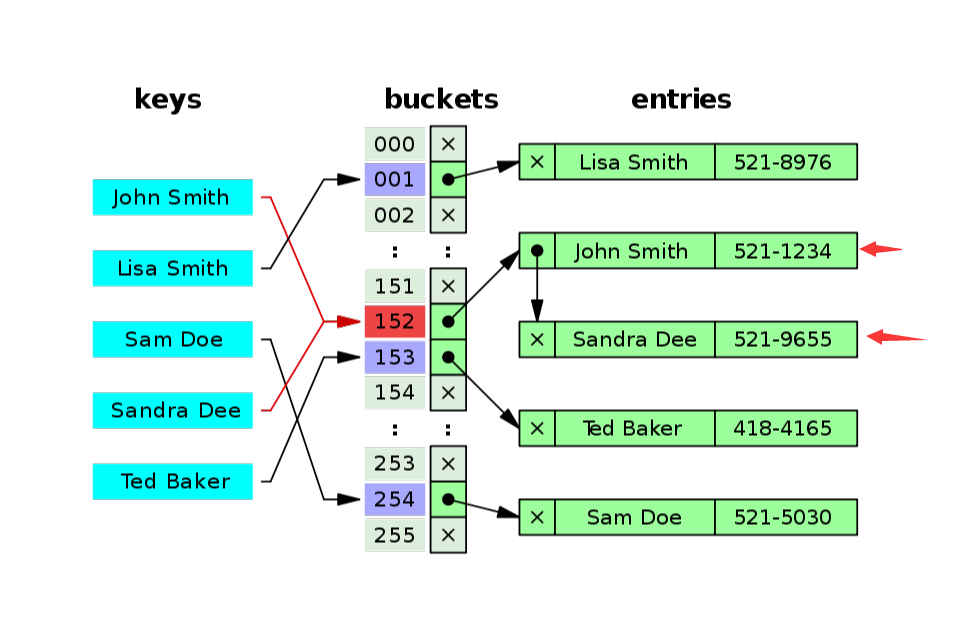
The following figure clearly explains the hash collision. It can be seen from the figure that Sandra Dee and John Smith fell to the position of 02 after hash operation, resulting in collision and conflict.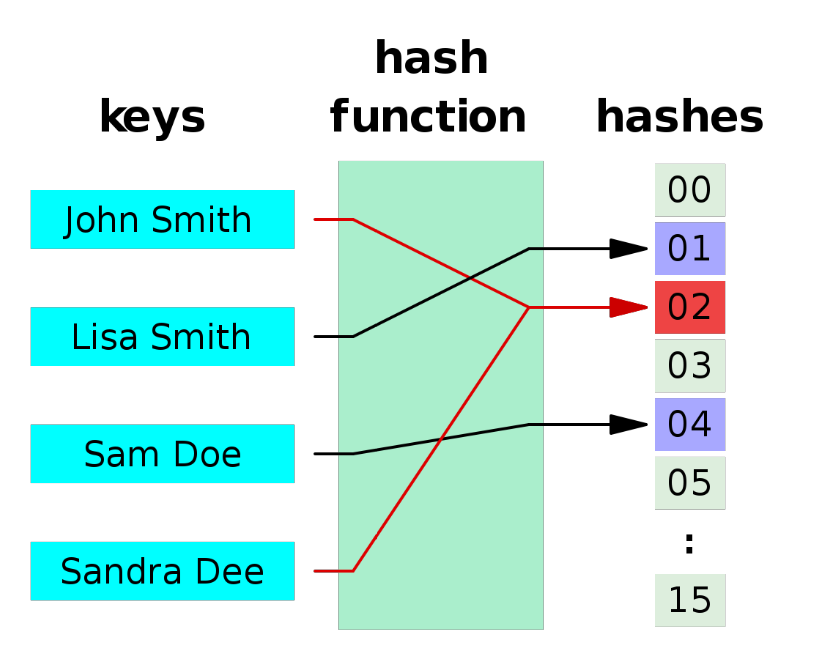
There are several common algorithms for constructing Hash functions.
1. Direct addressing method: take the value of keyword or a linear function of keyword as the hash address. That is, H(key)=key or H(key) = a • key + b, where a and b are constants (such hash functions are called self functions)
2. Numerical analysis method: analyze a group of data, such as the date of birth of a group of employees. At this time, we find that the first few digits of the date of birth are roughly the same. In this case, the probability of conflict will be very large. However, we find that the last few digits of the date of birth represent the month and the detailed date are very different. Suppose that the following digits are used to form the hash address, The probability of conflict will be significantly reduced. Therefore, digital analysis is to find out the law of numbers and use these data as much as possible to construct hash addresses with low probability of conflict.
3. Square middle method: take the middle digits after the square of keyword as the hash address.
4. Folding method: cut the keyword into several parts with the same number of digits, and the last part can have different digits, and then take the superposition and (remove the carry) of these parts as the hash address.
5. Random number method: select a random function and take the random value of keyword as the hash address. It is often used in situations with different length of keyword.
6. Divide and leave remainder method: take the remainder of the keyword divided by a number P not greater than the hash table length m as the hash address. That is, H (key) = key mod p, P < = M. It can not only take the module of keyword directly, but also take the module after folding and square operation. The choice of P is very important. It usually takes prime or M. if P is not selected well, it is easy to collide
2. Hash bucket algorithm
When it comes to Hash algorithm, you will think of Hash table. A Key can quickly Get hashCode through Hash function operation, and can directly Get Value through hashCode mapping. However, the Value of hashCode is generally very large, often more than 2 ^ 32, so it is impossible to specify a mapping for each hashCode.
Because of such a problem, people map the generated HashCode in the form of segments. Each segment is called a Bucket. Generally, the common Hash Bucket is to take the remainder of the result directly.
Assuming that the generated hashCode may have 2 ^ 32 values, and then it is cut into sections and mapped with 8 buckets, the algorithm of bucketindex = hashfunc (key1)% 8 can be used to determine which bucket this hashCode is mapped to.
As you can see, mapping is carried out in the form of hash bucket, which will aggravate hash conflict.
3. Conflict resolution algorithm
For a hash algorithm, conflict is inevitable, so how to deal with the conflict after it occurs is a key place. At present, common conflict resolution algorithms include zipper method (Dictionary Implementation), open addressing method, re hash method and public overflow partition method. This paper only introduces zipper method and re hash method, Students interested in other algorithms can refer to the references at the end of the article.
1. Zipper method: the idea of this method is to establish a single linked list of conflicting elements and store the head pointer address to the position of the bucket corresponding to the Hash table. In this way, after locating the position of the Hash table bucket, you can find the elements in the form of traversing the single linked list.
2. Re Hash method: as the name suggests, it is to use other Hash functions to Hash the key again until a non conflicting position is found.
There is a picture to describe the zipper method. The conflict is solved by establishing a single link list at the conflict position.
3, Dictionary implementation
The Dictionary implementation is mainly analyzed by comparing the source code. At present, the version of the source code is Net Framwork 4.7. You can stamp the address of the link source code: Link
This chapter mainly introduces several key classes and objects in Dictionary, and then follow the code to go through the process of insertion, deletion and capacity expansion. I believe you can understand its design principle.
1. Entry structure
First, we introduce an Entry structure. Its definition is shown in the following code. This is the smallest unit for storing data in a Dictionary. The elements added by calling the Add(Key,Value) method will be encapsulated in such a structure.
private struct Entry {
public int hashCode; // The 31 bit hashCode value other than the sign bit is - 1 if the Entry is not used
public int next; // The subscript index of the next element. If there is no next element, it will be - 1
public TKey key; // The key that holds the element
public TValue value; // Store the value of the element
}
2. Other key private variables
In addition to the Entry structure, there are several key private variables. Their definitions and explanations are shown in the following code.
private int[] buckets; // Hash bucket private Entry[] entries; // Entry array to hold elements private int count; // index location of current entries private int version; // The current version prevents the set from being changed during the iteration private int freeList; // The subscript index of the deleted Entry in the entries, which is free private int freeCount; // How many entries are deleted and how many free locations are there private IEqualityComparer<TKey> comparer; // comparator private KeyCollection keys; // Collection for storing keys private ValueCollection values; // Collection of values
In the above code, you should pay attention to the buckets and entries arrays, which are the key to the implementation of Dictionary.
3. Dictionary - Add operation
After the above analysis, I believe you don't particularly understand why you need to design and do so. Now let's go through the Add process of Dictionary and experience it.
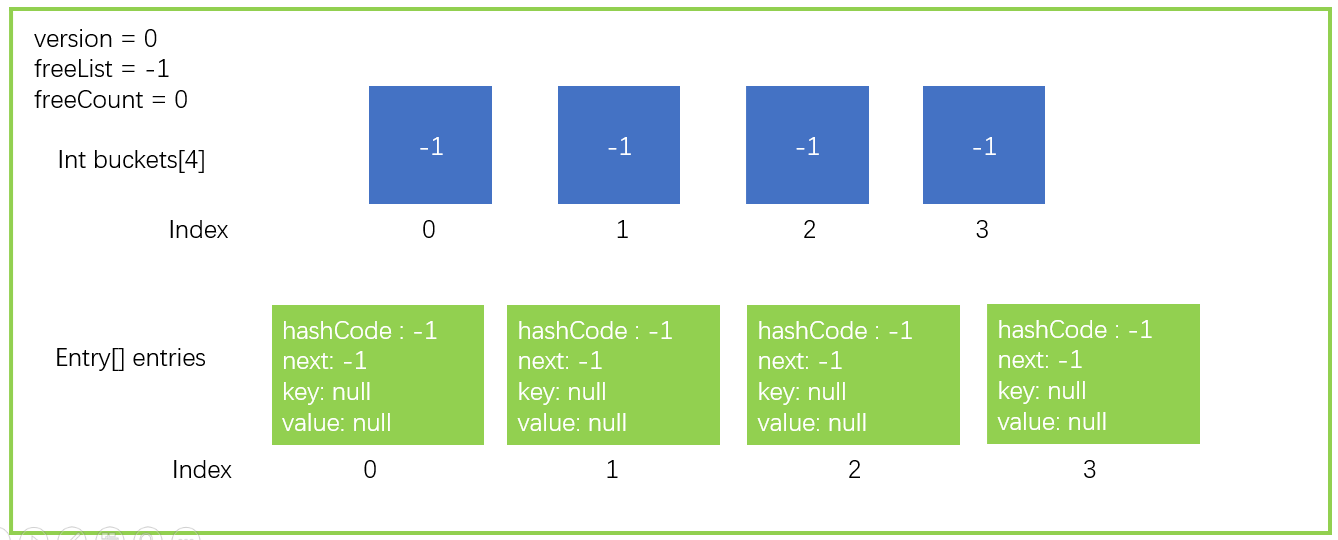
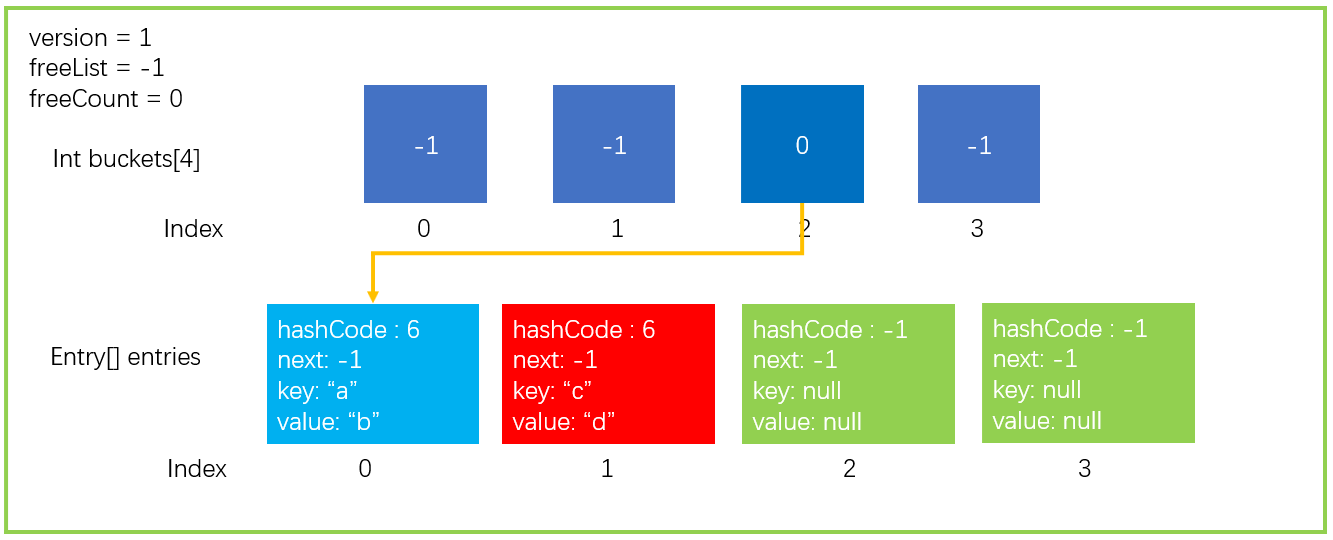
First, we describe the data structure of a Dictionary in the form of a graph, in which only the key points are drawn. A data structure with a bucket size of 4 and an Entry size of 4.
Then we assume that we need to perform an add operation, dictionary Add ("a", "B"), where key = "a",value = "b".
-
According to the value of key, calculate its hashCode. We assume that the hash value of "a" is 6 (GetHashCode("a") = 6).
-
Calculate the bucket in which the hashCode falls through the remainder operation of the hashCode. Now the bucket length (buckets.Length) is 4, so it is 6% 4. Finally, it falls into the bucket with index 2, that is, buckets[2].
-
To avoid other situations, it will store hashCode, key, value and other information in entries[count], because the count location is idle; Continue count + + to point to the next free location. The first location in the figure above, index=0, is idle, so it is stored in the location of entries[0].
-
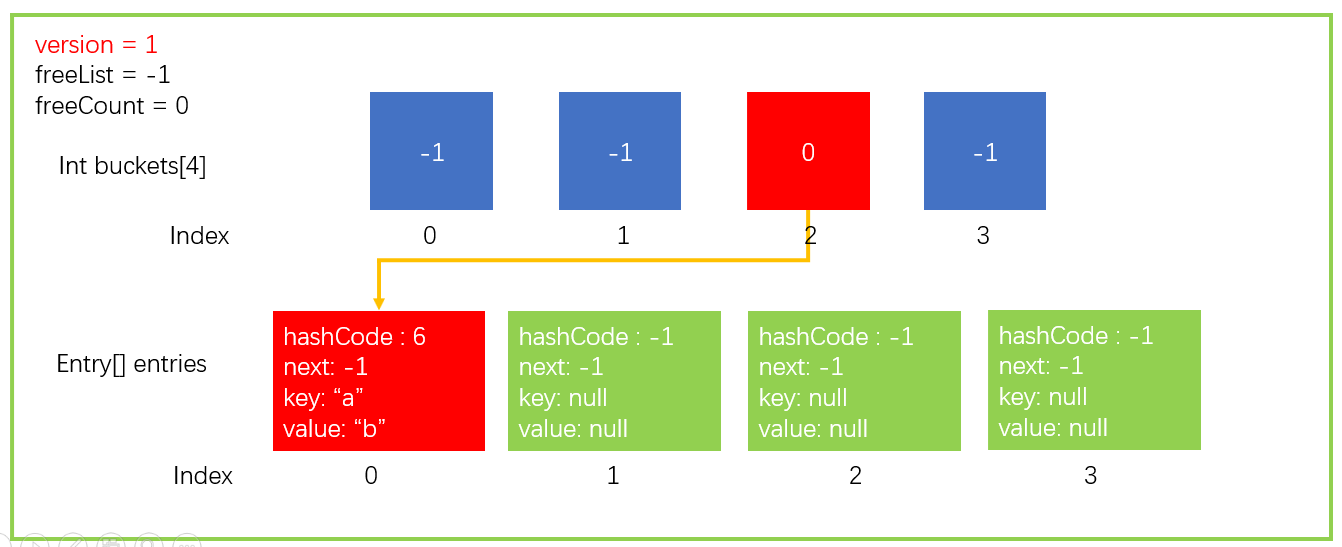
Assign the subscript entryIndex of Entry to the bucket corresponding to the subscript in buckets. In step 3, it is stored in entries[0], so buckets[2]=0.
-
Finally, version + +, the set has changed, so the version needs + 1. Only adding, replacing, and deleting elements will update the version
Steps 1 to 5 above are just for your understanding. In fact, there are some deviations, which will be supplemented in the Add operation section later.
After completing the above Add operation, the data structure is updated to the form shown in the figure below.
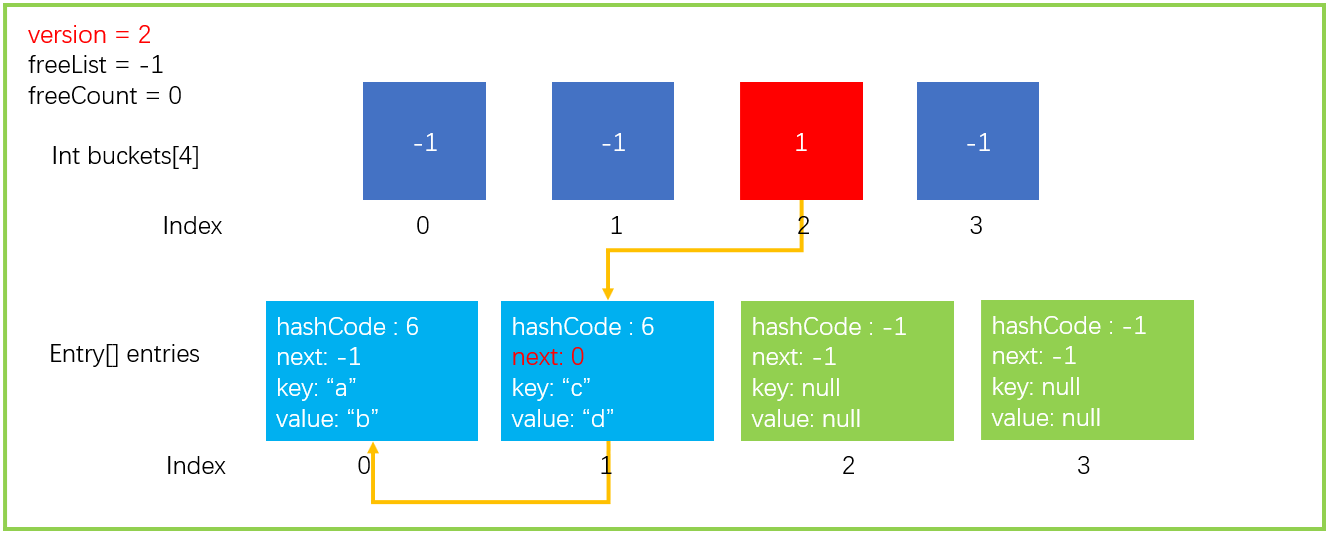
This is an ideal operation. There is only one hashCode in a bucket without collision, but in fact, collisions often occur; So how to solve the collision in the Dictionary class.
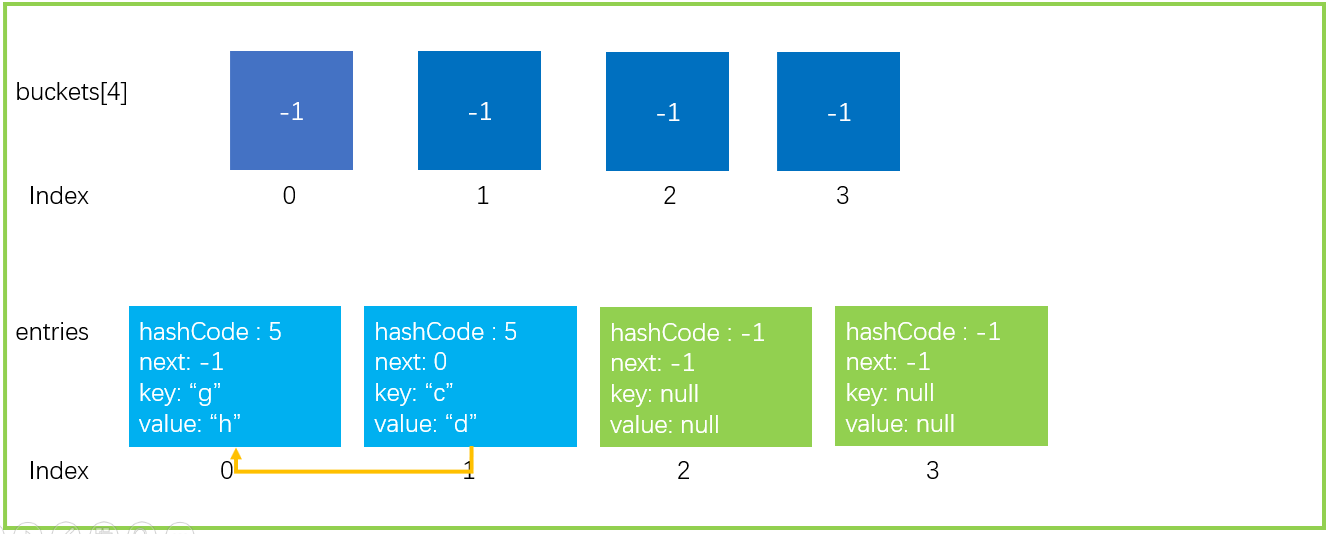
We continue to perform an add operation, dictionary Add ("c", "d"), assuming GetHashCode("c") = 6, the last 6% 4 = 2. The index of the last bucket is also 2. There is no problem according to the previous steps 1 ~ 3. After execution, the data structure is shown in the figure below.
If you continue with step 4, then buckets[2] = 1, and then the relationship between the original buckets [2] = > entries [0] will be lost, which is something we don't want to see. Now the next in Entry plays a big role.
If other elements of the corresponding buckets[index] already exist, the following two statements will be executed to make the new entry Next points to the previous element and buckets[index] points to the new element, forming a single linked list.
entries[index].next = buckets[targetBucket]; ... buckets[targetBucket] = index;
In fact, step 4 is to do such an operation without judging whether there are other elements, because the initial value of the bucket in buckets is - 1, which will not cause problems.
After the above steps, the data structure will be updated to the following figure.
4. Dictionary - Find operation
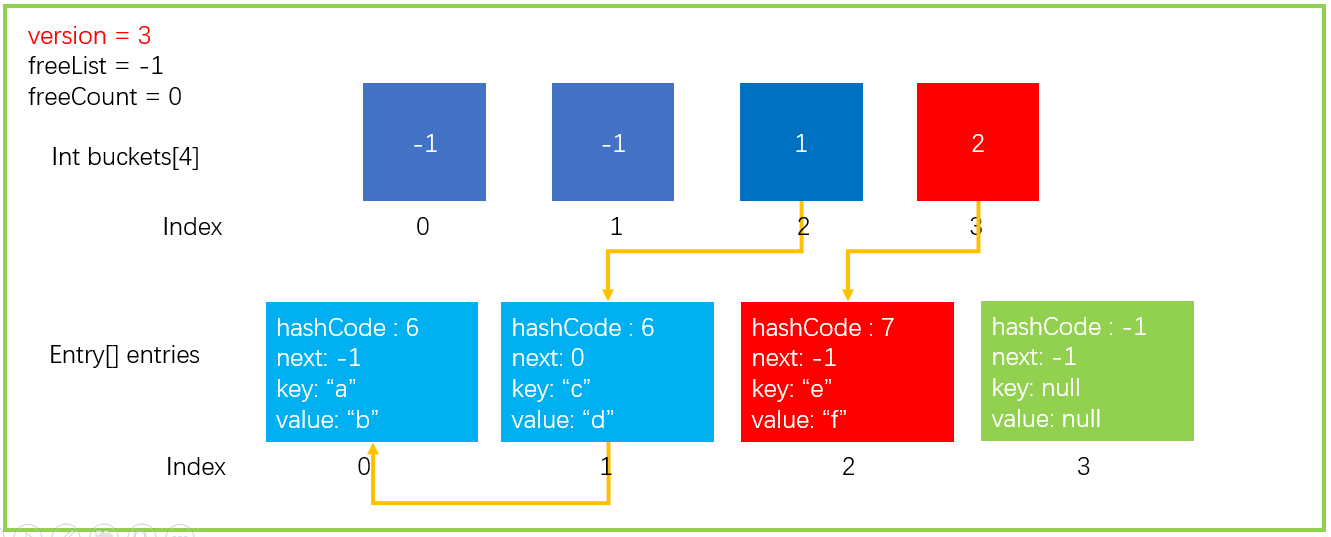
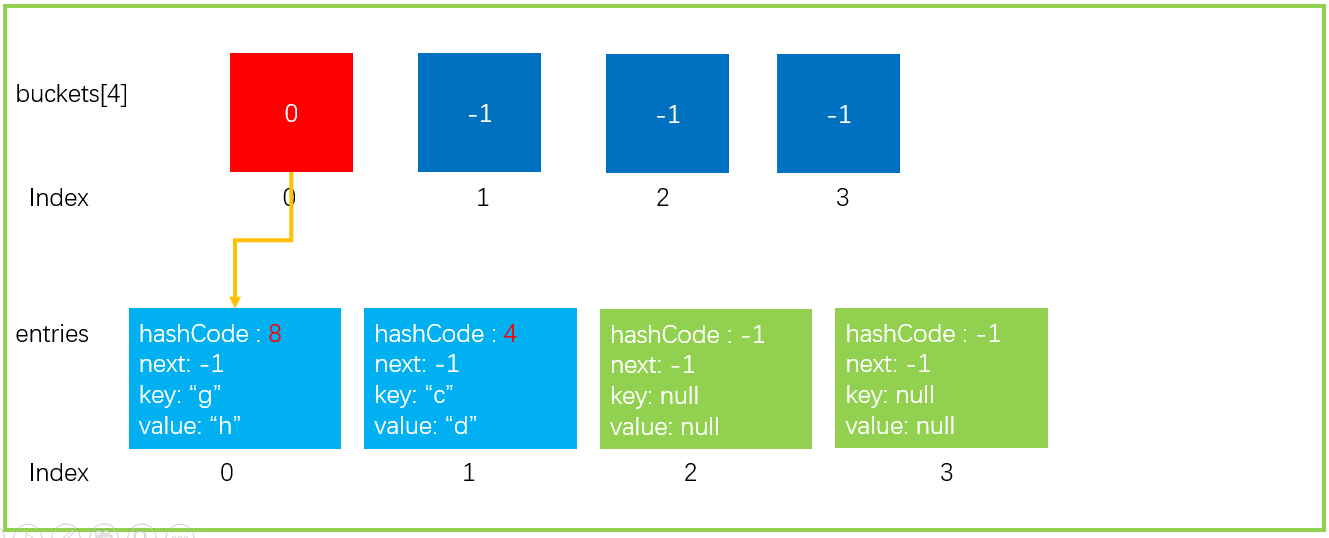
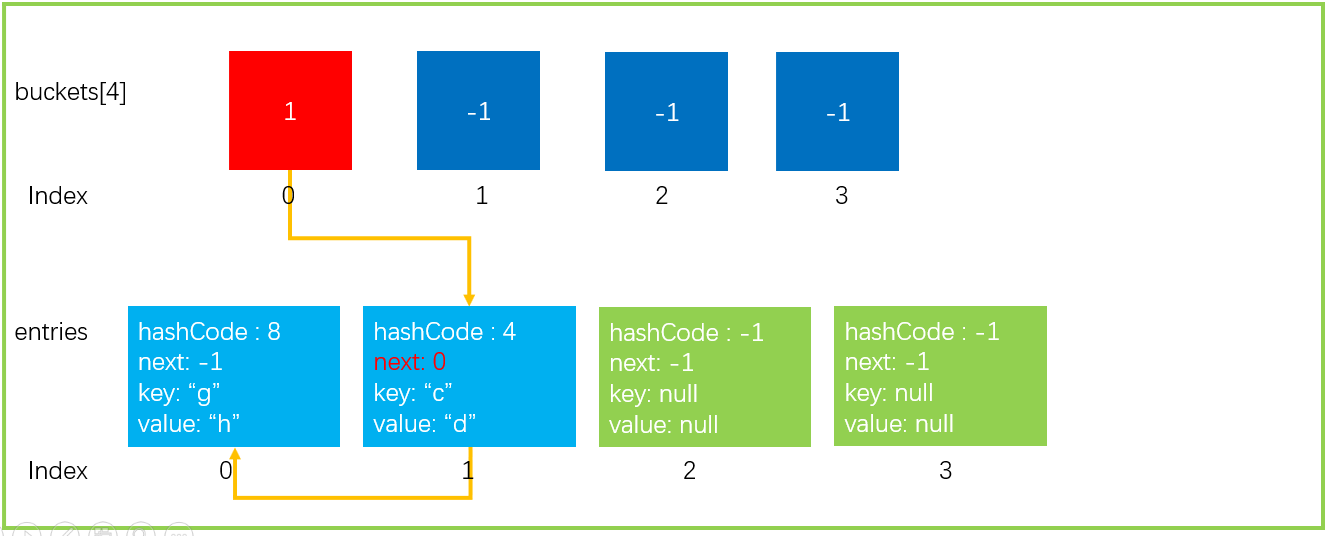
To facilitate the demonstration of how to find, we continue to add an element dictionary Add("e","f"),GetHashCode(“e”) = 7; 7% buckets.Length=3, and the data structure is as follows.
Suppose we now execute such a statement as dictionary Getvalueordefault ("a"), the following steps will be performed
- Get the hashCode of the key and calculate the bucket position. As we mentioned earlier, hashCode of "a" is 6, so targetBucket=2 is finally calculated.
- Find entries[1] through buckets[2]=1, compare whether the values of keys are equal, and return entryIndex if they are equal. If you don't want to wait, continue to search entries[next] until you find the equal elements of keys or next == -1. Here we find the element with key == "a" and return entryIndex=0.
- If entryindex > = 0, the corresponding entries[entryIndex] element is returned; otherwise, default(TValue) is returned. Here we directly return to entries [0] value.
The whole search process is shown in the figure below
Extract the code you are looking for, as shown below.
// Find the location of the Entry element
private int FindEntry(TKey key) {
if( key == null) {
ThrowHelper.ThrowArgumentNullException(ExceptionArgument.key);
}
if (buckets != null) {
int hashCode = comparer.GetHashCode(key) & 0x7FFFFFFF; // Get HashCode, ignoring sign bit
// Int i = buckets [hashcode% buckets. Length] find the corresponding bucket and get the position of entry in entries
// i >= 0; i = entries[i]. Next traverse single linked list
for (int i = buckets[hashCode % buckets.Length]; i >= 0; i = entries[i].next) {
// Find it and return
if (entries[i].hashCode == hashCode && comparer.Equals(entries[i].key, key)) return i;
}
}
return -1;
}
...
internal TValue GetValueOrDefault(TKey key) {
int i = FindEntry(key);
// Greater than or equal to 0 means that the element position is found and directly returns value
// Otherwise, the default value of this type is returned
if (i >= 0) {
return entries[i].value;
}
return default(TValue);
}
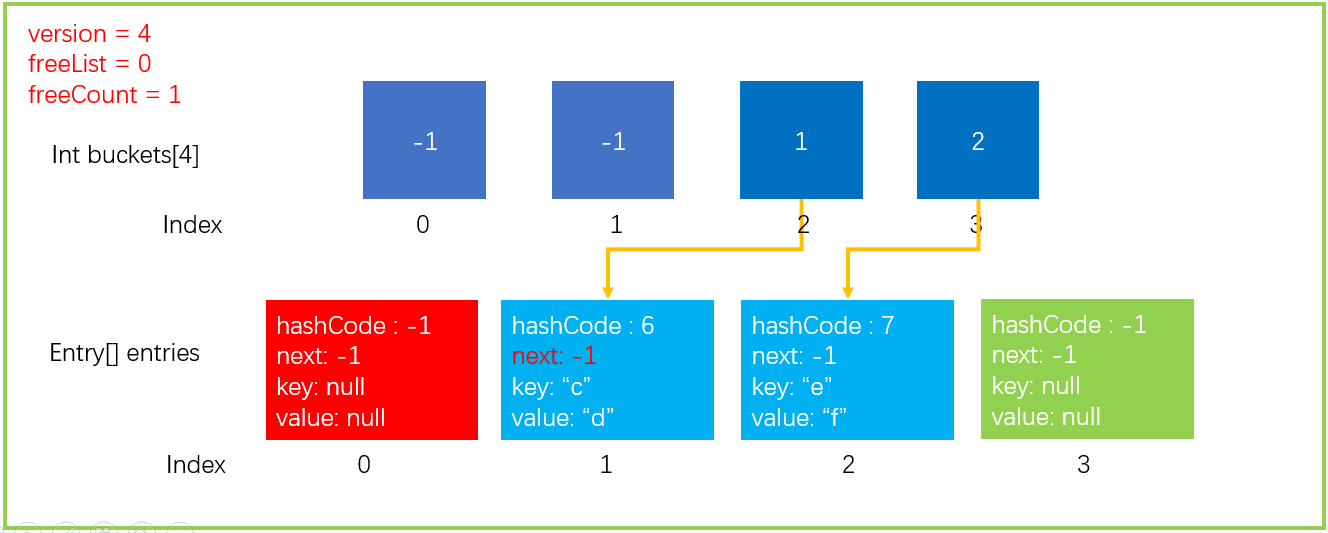
5. Dictionary - Remove operation
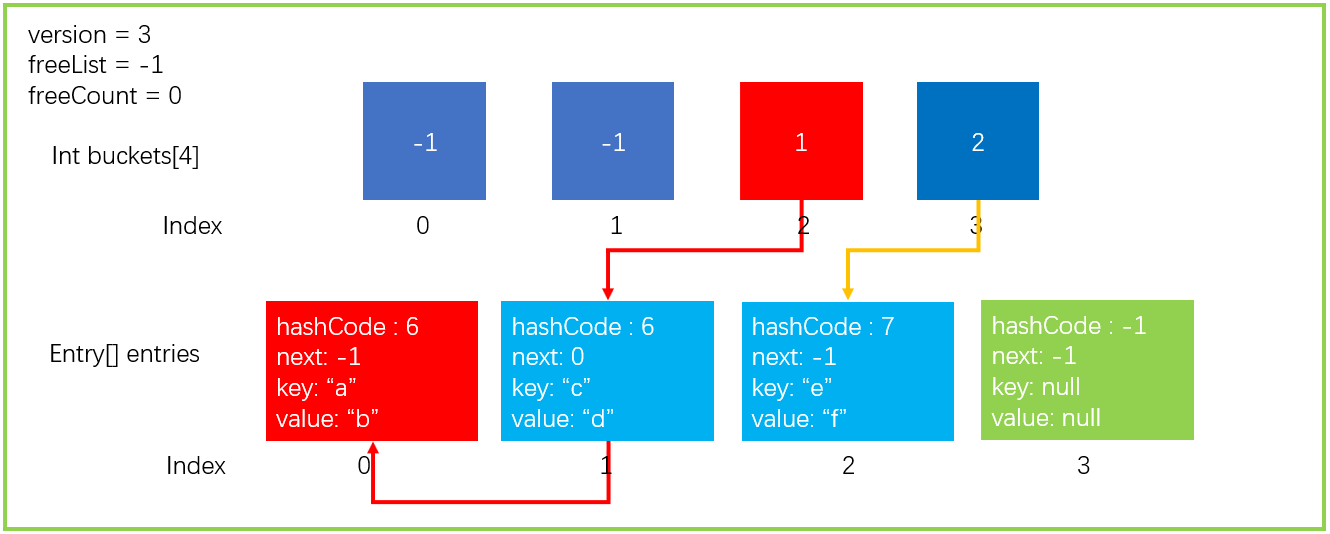
I've already introduced adding and searching. Next, I'll introduce how to delete a Dictionary. We use the previous Dictionary data structure.
The previous steps of deleting are similar to searching. You need to find the location of the element and then delete it.
We now execute such a statement as dictionary Remove ("a"), the hashFunc operation result is consistent with the above. Most of the steps are similar to searching. Let's directly look at the extracted code, as shown below.
public bool Remove(TKey key) {
if(key == null) {
ThrowHelper.ThrowArgumentNullException(ExceptionArgument.key);
}
if (buckets != null) {
// 1. Get hashCode through key
int hashCode = comparer.GetHashCode(key) & 0x7FFFFFFF;
// 2. Get the bucket position by taking the remainder
int bucket = hashCode % buckets.Length;
// Last is used to determine whether the current bucket is the last element in the single linked list
int last = -1;
// 3. Traverse the single linked list corresponding to the bucket
for (int i = buckets[bucket]; i >= 0; last = i, i = entries[i].next) {
if (entries[i].hashCode == hashCode && comparer.Equals(entries[i].key, key)) {
// 4. After finding the element, if last < 0 means that it is the last element in the bucket, then directly assign the subscript in the bucket to entries [i] Next
if (last < 0) {
buckets[bucket] = entries[i].next;
}
else {
// 4.1 last is not less than 0, which means that the current element is in the middle of the bucket single linked list. It is necessary to connect the head node and tail node of the element to prevent the interruption of the linked list
entries[last].next = entries[i].next;
}
// 5. Initialize the data in the Entry structure
entries[i].hashCode = -1;
// 5.1 create freeList single linked list
entries[i].next = freeList;
entries[i].key = default(TKey);
entries[i].value = default(TValue);
// *6. For the key code, freeList is equal to the current entry position, and the next Add element will be added to this position first
freeList = i;
freeCount++;
// 7. Version number + 1
version++;
return true;
}
}
}
return false;
}
After executing the above code, the data structure will be updated as shown in the figure below. Note that the values of variable, freeList and freeCount have been updated.
6. Dictionary - Resize operation (capacity expansion)
A careful partner may want to ask after reading the Add operation. Buckets and entries are just two arrays. What if the array is full? The next step is the Resize operation I want to introduce to expand our buckets and entries.
6.1 trigger conditions for capacity expansion
First, we need to know under what circumstances capacity expansion will occur; The first case is that the array is full and there is no way to store new elements. As shown in the figure below.
As we all know from the above, Hash operation will inevitably lead to conflict. The zipper method is used in Dictionary to solve the conflict, but look at this situation in the figure below.
All elements just fall on buckets[3], resulting in time complexity O(n) and search performance degradation; Therefore, the second is that too many collisions occur in the Dictionary, which will seriously affect the performance and trigger the capacity expansion operation.
At present The number of collisions threshold set in net framework 4.7 is 100
public const int HashCollisionThreshold = 100;
6.2 how to expand capacity
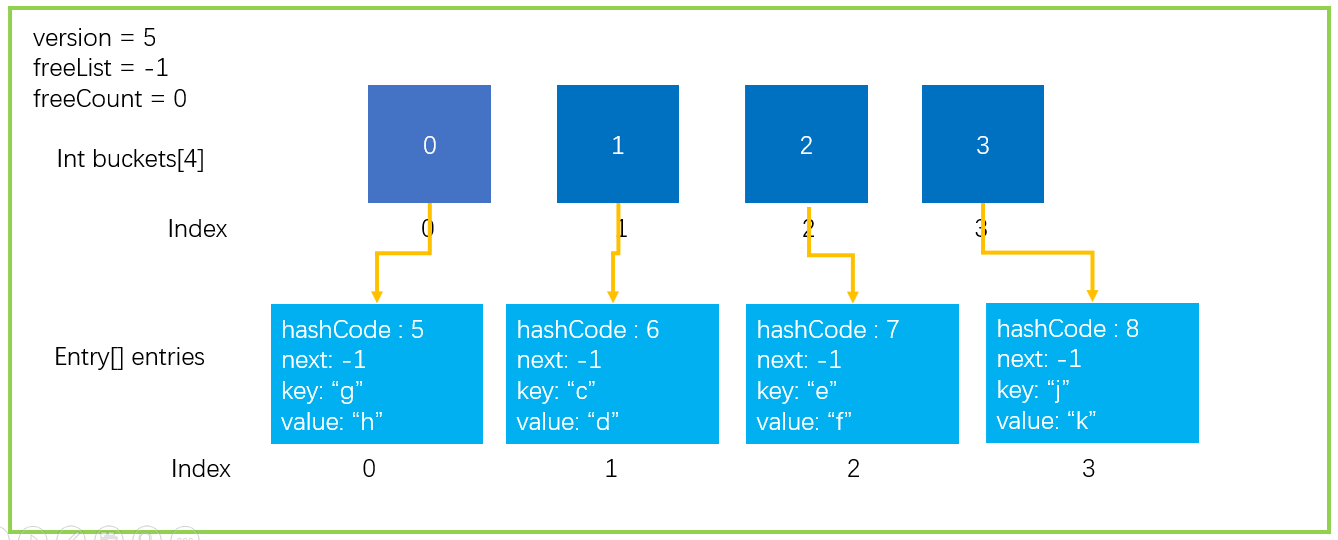
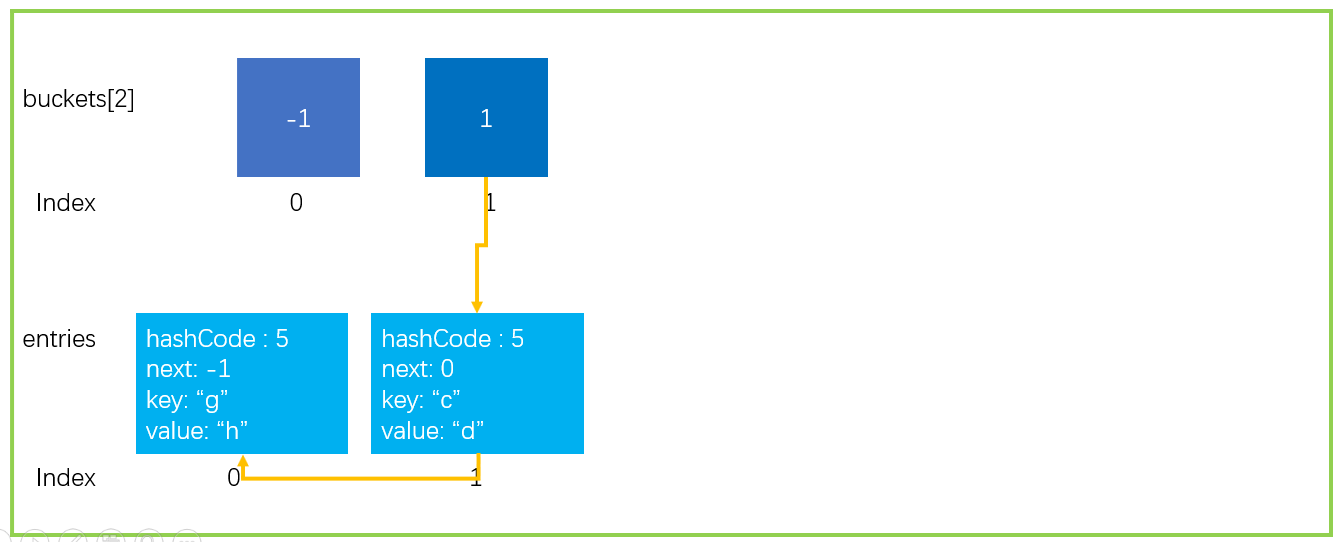
In order to show you clearly, the following data structure is simulated. A Dictionary with a size of 2 is assumed, and the collision threshold is 2; Now trigger Hash collision expansion.
Start capacity expansion.
1. Apply for buckets and entries twice the current size
2. Copy the existing elements to the new entries
After completing the above two steps, the new data structure is as follows.
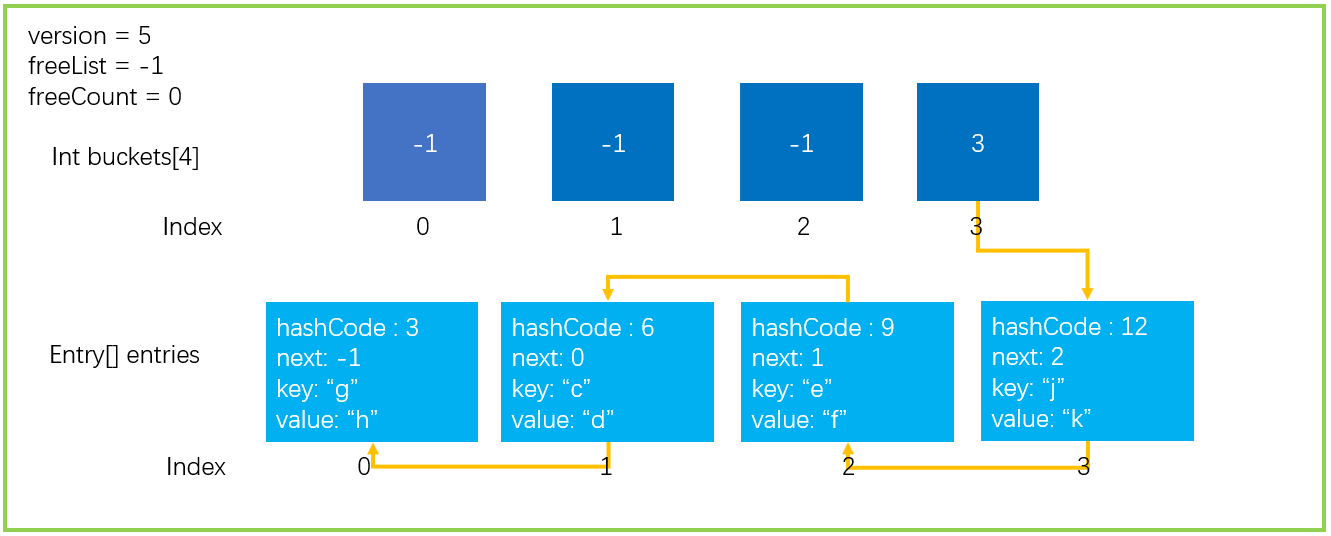
3. If it is a Hash collision expansion, use the new HashCode function to recalculate the Hash value
As mentioned above, this is a Hash collision expansion, so it is necessary to use the new Hash function to calculate the Hash value. The new Hash function will not solve the collision problem. It may be worse. The same as in the figure below will still fall on the same bucket.
4. For each element of entries, bucket = newentries [i] Hashcode% newsize determines the location of new buckets
**5. Rebuild hash chain, newentries [i] next=buckets[bucket]; buckets[bucket]=i; **
Since buckets have also been expanded to twice the size, it is necessary to re determine which bucket the hashCode is in; Finally, rebuild the hash list
This completes the expansion operation. If the expansion is triggered by reaching the Hash collision threshold, the result may be worse after the expansion.
In JDK, if HashMap collides too many times, it will convert the single linked list into a red black tree to improve the search performance. At present There is no such optimization in net framework Net Core already has similar optimizations and will have time to share in the future Net Core.
Each capacity expansion operation needs to traverse all elements, which will affect the performance. Therefore, it is best to set an estimated initial size when creating a Dictionary instance.
private void Resize(int newSize, bool forceNewHashCodes) {
Contract.Assert(newSize >= entries.Length);
// 1. Apply for new Buckets and entries
int[] newBuckets = new int[newSize];
for (int i = 0; i < newBuckets.Length; i++) newBuckets[i] = -1;
Entry[] newEntries = new Entry[newSize];
// 2. Copy the elements in the entries to the new entries
Array.Copy(entries, 0, newEntries, 0, count);
// 3. If it is a Hash collision expansion, use the new HashCode function to recalculate the Hash value
if(forceNewHashCodes) {
for (int i = 0; i < count; i++) {
if(newEntries[i].hashCode != -1) {
newEntries[i].hashCode = (comparer.GetHashCode(newEntries[i].key) & 0x7FFFFFFF);
}
}
}
// 4. Determine the new bucket location
// 5. Rebuild Hahs single linked list
for (int i = 0; i < count; i++) {
if (newEntries[i].hashCode >= 0) {
int bucket = newEntries[i].hashCode % newSize;
newEntries[i].next = newBuckets[bucket];
newBuckets[bucket] = i;
}
}
buckets = newBuckets;
entries = newEntries;
}
7. Dictionary - Add operation
In our previous Add operation steps, we mentioned such a paragraph. Here, we mentioned that there will be another case, that is, the element will be deleted.
- To avoid other situations, it will store hashCode, key, value and other information in entries[count], because the count location is idle; Continue count + + to point to the next free location. The first location in the figure above, index=0, is idle, so it is stored in the location of entries[0].
Because count points to the next free entry in entries [] by self increment, if an element is deleted, a free entry will appear in the position before count; If not, a lot of space will be wasted.
This is why the Remove operation records freeList and freeCount in order to make use of the deleted space. In fact, the Add operation will give priority to the free entry location of freeList. The excerpt code is as follows.
private void Insert(TKey key, TValue value, bool add){
if( key == null ) {
ThrowHelper.ThrowArgumentNullException(ExceptionArgument.key);
}
if (buckets == null) Initialize(0);
// Get hashCode through key
int hashCode = comparer.GetHashCode(key) & 0x7FFFFFFF;
// Calculate the target bucket subscript
int targetBucket = hashCode % buckets.Length;
// Number of collisions
int collisionCount = 0;
for (int i = buckets[targetBucket]; i >= 0; i = entries[i].next) {
if (entries[i].hashCode == hashCode && comparer.Equals(entries[i].key, key)) {
// If it is an add operation and the same element is traversed, an exception is thrown
if (add) {
ThrowHelper.ThrowArgumentException(ExceptionResource.Argument_AddingDuplicate);
}
// If it is not an increase operation, it may be an index assignment operation. dictionary["foo"] = "foo"
// Then the assigned version + +, exit
entries[i].value = value;
version++;
return;
}
// Every element traversed is a collision
collisionCount++;
}
int index;
// If there is a deleted element, put the element in the free position of the deleted element
if (freeCount > 0) {
index = freeList;
freeList = entries[index].next;
freeCount--;
}
else {
// If the current entries are full, the capacity expansion is triggered
if (count == entries.Length)
{
Resize();
targetBucket = hashCode % buckets.Length;
}
index = count;
count++;
}
// Assign value to entry
entries[index].hashCode = hashCode;
entries[index].next = buckets[targetBucket];
entries[index].key = key;
entries[index].value = value;
buckets[targetBucket] = index;
// Version number++
version++;
// If the number of collisions is greater than the set maximum number of collisions, the Hash collision expansion will be triggered
if(collisionCount > HashHelpers.HashCollisionThreshold && HashHelpers.IsWellKnownEqualityComparer(comparer))
{
comparer = (IEqualityComparer<TKey>) HashHelpers.GetRandomizedEqualityComparer(comparer);
Resize(entries.Length, true);
}
}
The above is the complete Add code, or is it very simple, right?
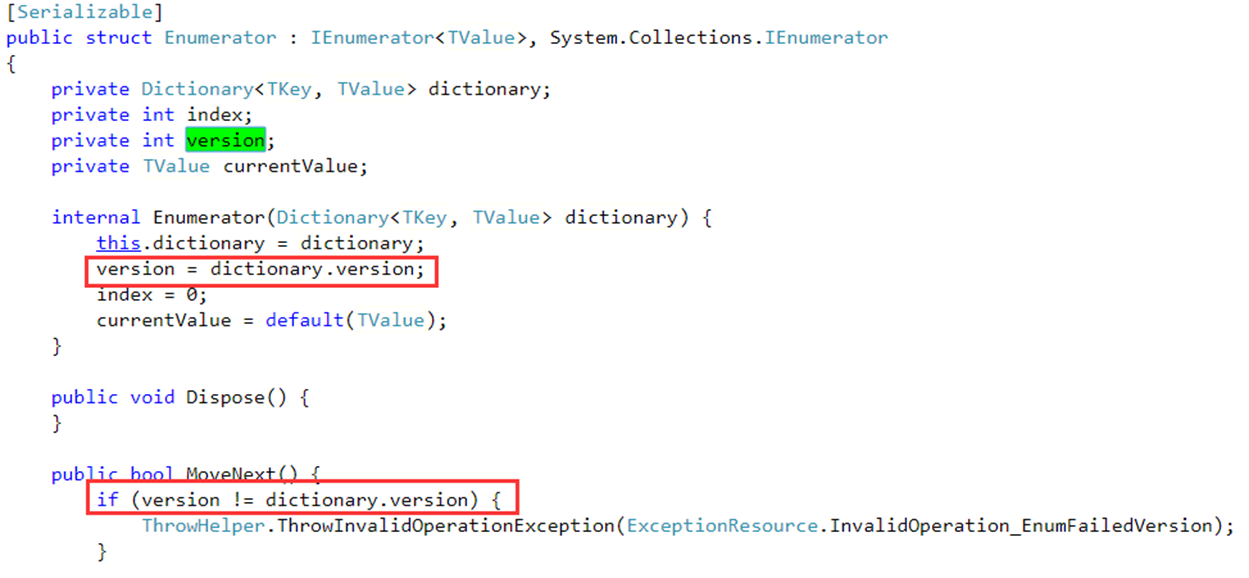
8. Collection version control
The variable version has been mentioned all the time above. It will make version + + when adding, modifying and deleting each time; So what is the meaning of this version?
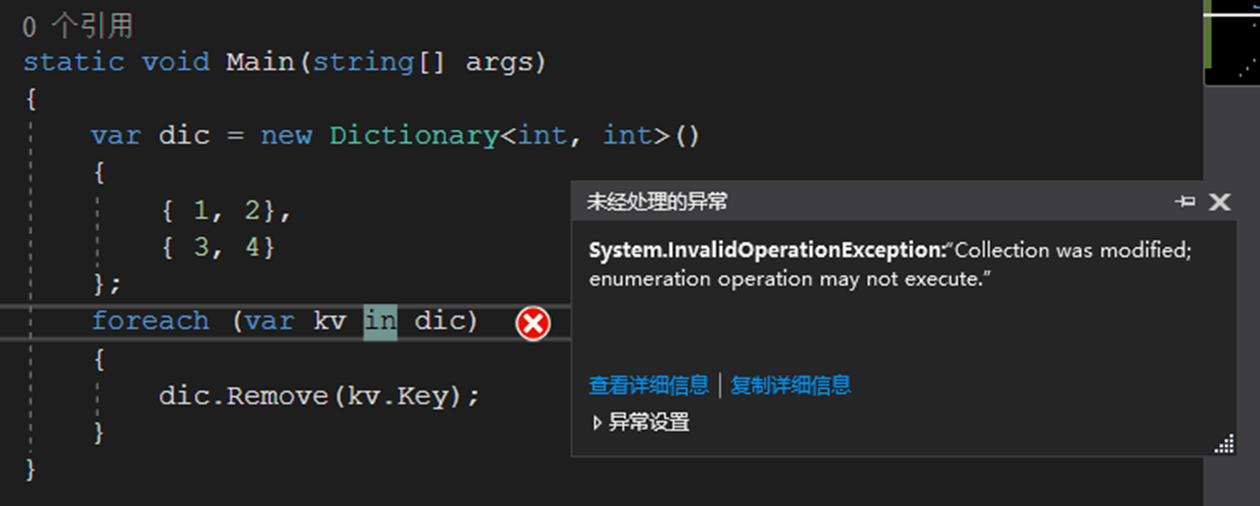
First, let's look at a piece of code. In this code, we first instantiate a Dictionary instance, then traverse the instance through foreach, and use DIC in the foreach code block Remove (kV. Key) deletes the element.
The result is a system InvalidOperationException:"Collection was modified..." For such exceptions, the set is not allowed to change during the iteration. If you directly delete elements after traversing in Java, there will be a strange problem, so Net uses version to realize version control.
So how to implement version control in the iterative process? Let's take a look at the source code and know it clearly.
When the iterator initializes, a dictionary is recorded Version version number, and then each iteration process will check whether the version number is consistent. If it is inconsistent, an exception will be thrown.
This avoids modifying the set in the iterative process, resulting in many strange problems.
4, References and summary
In the process of writing this paper, we mainly refer to the following literature. Thank its author for his contribution to knowledge sharing!
- http://www.cnblogs.com/mengfanrong/p/4034950.html
- https://en.wikipedia.org/wiki/Hash_table
- https://www.cnblogs.com/wuchaodzxx/p/7396599.html
- https://www.cnblogs.com/liwei2222/p/8013367.html
- https://referencesource.microsoft.com/#mscorlib/system/collections/generic/dictionary.cs,fd1acf96113fbda9
The author's level is limited. If you make mistakes, you are welcome to criticize and correct!
Author: InCerry
source: https://www.cnblogs.com/InCerry/p/10325290.html
Copyright: this work adopts Signature - non commercial use - share 4.0 international in the same way License under the license agreement.